Solution des exercices : Application affine 3e
Classe:
Troisième
Exercice 1
$f$ est une application linéaire définie dans $\mathbb{R}$ telle que : $f(3)=-6.
$g$ est une application affine définie dans $\mathbb{R}$ telle que : $g(5)=-2\;;\ g(-3)=4.$
1) Écrivons $f(x)\ $ et $\ g(x)$ en fonction de $x.$
En effet, comme $f$ est une application linéaire définie dans $\mathbb{R}$ alors, $f$ est de la forme :
$$f(x)=ax$$
avec $a$ son coefficient linéaire.
On a alors : $f(3)=3a$
Or, on sait que $f(3)=-6$
Donc, $3a=-6$
Ce qui donne : $a=-\dfrac{6}{3}=-2$
D'où, $\boxed{f(x)=-2x}$
Déterminons l'application affine $g.$
En effet, comme $g$ est une application affine définie dans $\mathbb{R}$ alors, $g$ est de la forme :
$$g(x)=ax+b$$
avec $a$ son coefficient directeur et $b$ son ordonnée à l'origine.
Or, on sait que : $g(5)=-2\ $ et $\ g(-3)=4.$
Alors, le coefficient directeur $a$ est donné par :
$\begin{array}{rcl} a&=&\dfrac{g(-3)-g(5)}{(-3)-(5)}\\\\&=&\dfrac{(4)-(-2)}{-3-5}\\\\&=&\dfrac{6}{-8}\\\\&=&-\dfrac{3}{4}\end{array}$
Donc, $g(x)=-\dfrac{3}{4}x+b$
Pour déterminer $b$, on peut calculer $g(5)\ $ ou $\ g(-3)$ à partir de l'expression de $g(x).$
On a : $g(5)=-\dfrac{3}{4}\times 5+b$
Or, $g(5)=-2$ donc, $-\dfrac{15}{4}+b=-2$
Ce qui donne :
$\begin{array}{rcl} b&=&-2+\dfrac{15}{4}\\\\&=&-\dfrac{8}{4}+\dfrac{15}{4}\\\\&=&\dfrac{7}{4}\end{array}$
D'où, $\boxed{g(x)=-\dfrac{3}{4}x+\dfrac{7}{4}}$
2) Donnons le sens de variation de $f\ $ et $\ g.$
D'après le résultat de la question $1)$, on a : $f(x)=-2x.$
Donc, $f$ est une application linéaire de coefficient linéaire $-2<0.$
Par conséquent, $f$ est décroissante.
D'après le résultat de la question $1)$, on a : $g(x)=-\dfrac{3}{4}x+\dfrac{7}{4}.$
Considérons alors $g_{1}$, l'application linéaire associée à $g$ et définie par :
$$g_{1}(x)=-\dfrac{3}{4}x$$
Comme le coefficient linéaire de $g_{1}$ est négatif alors, $g$ est décroissante.
Exercice 2
On considère les expressions suivantes :
$$H(x)=4(x+\sqrt{3})^{2}-4\sqrt{3}(x+\sqrt{3})+3\ \text{ et }\ G(x)=(2x+\sqrt{3})^{2}$$
1) Nous allons développer, réduire puis ordonner $H(x)\ $ et $\ G(x)$
On a :
$\begin{array}{rcl} H(x)&=&4(x+\sqrt{3})^{2}-4\sqrt{3}(x+\sqrt{3})+3\\\\&=&4x^{2}+8x\sqrt{3}+12-4x\sqrt{3}-12+3\\\\&=&4x^{2}+4x\sqrt{3}+3\end{array}$
Donc, $\boxed{H(x)=4x^{2}+4x\sqrt{3}+3}$
Soit :
$\begin{array}{rcl} G(x)&=&(2x+\sqrt{3})^{2}\\\\&=&4x^{2}+4x\sqrt{3}+3\end{array}$
Alors, $\boxed{G(x)=4x^{2}+4x\sqrt{3}+3}$
2) En déduisons une factorisation de $H(x).$
D'après le résultat de la question $1)$, on constate que :
$$H(x)=G(x)$$
Or, $G(x)=(2x+\sqrt{3})^{2}$
Donc, $\boxed{H(x)=(2x+\sqrt{3})^{2}}$
3) On pose : $Q(x)=\sqrt{H(x)}.$
a) Résolvons dans $\mathbb{R}$ l'équation $Q(x)=2\sqrt{3}.$
On a : $Q(x)=2\sqrt{3}$ si, et seulement si, $\sqrt{H(x)}=2\sqrt{3}$
Donc, $\sqrt{(2x+\sqrt{3})^{2}}=2\sqrt{3}$
Or, $\sqrt{(2x+\sqrt{3})^{2}}=\left|(2x+\sqrt{3})\right|$
Ce qui revient donc à résoudre l'équation : $|(2x+\sqrt{3})|=2\sqrt{3}$
En utilisant la propriété de la valeur absolue, on a :
$\begin{array}{rcl}\left|(2x+\sqrt{3})\right|=2\sqrt{3}&\Leftrightarrow&2x+\sqrt{3}=2\sqrt{3}\ \text{ ou }\ 2x+\sqrt{3}=-2\sqrt{3}\\\\&\Leftrightarrow&2x=2\sqrt{3}-\sqrt{3}\ \text{ ou }\ 2x=-2\sqrt{3}-\sqrt{3}\\\\&\Leftrightarrow&2x=\sqrt{3}\ \text{ ou }\ 2x=-3\sqrt{3}\\\\&\Leftrightarrow&x=\dfrac{\sqrt{3}}{2}\ \text{ ou }\ x=-\dfrac{3\sqrt{3}}{2}\end{array}$
Donc, $\left|(2x+\sqrt{3})\right|=2\sqrt{3}$ si, et seulement si, $x=\dfrac{\sqrt{3}}{2}\ $ ou $\ x=-\dfrac{3\sqrt{3}}{2}$
D'où, l'équation $Q(x)=2\sqrt{3}$ a pour solution dans $\mathbb{R}\ :$
$$S=\left\lbrace\dfrac{\sqrt{3}}{2}\;;\ -\dfrac{3\sqrt{3}}{2}\right\rbrace$$
b) Montrons que $Q$ est une application affine par intervalle.
Soit : $Q(x)=\sqrt{(2x+\sqrt{3})^{2}}=\left|(2x+\sqrt{3})\right|$
Étudions alors le signe de $(2x+\sqrt{3})$
On a : $2x+\sqrt{3}=0$ si, et seulement si, $x=-\dfrac{\sqrt{3}}{2}$
Donc, $(2x+\sqrt{3})$ est positif pour tout $x>-\dfrac{\sqrt{3}}{2}$ et négatif pour $x<-\dfrac{\sqrt{3}}{2}.$
En regroupant ces informations dans un tableau de signes, on obtient :
$$\begin{array}{|c|lcccr|}\hline x&-\infty& &-\sqrt{3}/2& &+\infty \\ \hline\text{signe de }(2x+\sqrt{3})& &-&|&+& \\ \hline Q(x)& &-(2x+\sqrt{3})&0&(2x+\sqrt{3})& \\ \hline\end{array}$$
Donc,
$-\ $ si $x\in\;\left]-\infty\;;\ -\dfrac{\sqrt{3}}{2}\right]\;,\ \ Q(x)=-2x-\sqrt{3}$
$-\ $ si $x\in\;\left[-\dfrac{\sqrt{3}}{2}\;;\ +\infty\right[\;,\ \ Q(x)=2x+\sqrt{3}$
D'où, $Q$ est une application affine par intervalle.
c) Représentons graphiquement $Q$ dans un repère orthonormé $(O\;,\ I\;,\ J).$
En effet, représenter graphiquement $Q$ revient tout simplement à représenter les droites :
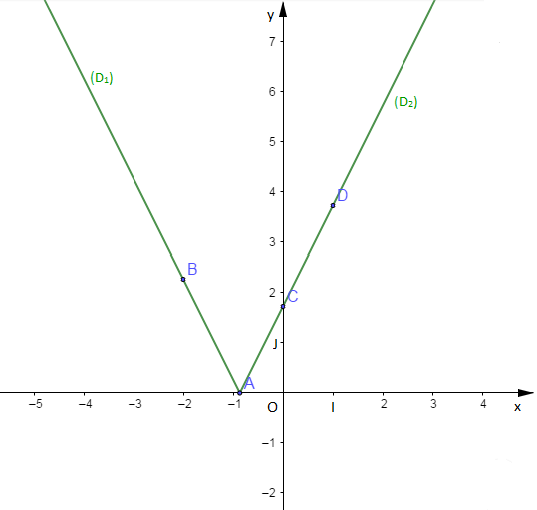
$(D_{1})\ :\ y=-2x-\sqrt{3}$ dans l'intervalle $\left]-\infty\;;\ -\dfrac{\sqrt{3}}{2}\right]$
$(D_{2})\ :\ y=2x+\sqrt{3}$ dans l'intervalle $\left[-\dfrac{\sqrt{3}}{2}\;;\ +\infty\right[$
Choisissons alors deux points $A\;,\ B\in(D_{1})$ et deux points $C\;,\ D\in(D_{2})$
Soit :
$$\begin{array}{|c|c|c|}\hline&A&B \\ \hline x&-\sqrt{3}/2&-2 \\ \hline y&0&4-\sqrt{3} \\ \hline \end{array}\qquad\qquad \begin{array}{|c|c|c|}\hline&C&D \\ \hline x&0&1 \\ \hline y&\sqrt{3}&2+\sqrt{3} \\ \hline\end{array}$$
Traçons alors la droite $(D_{1})$ passant par $A\;,\ B\ $ et la droite $(D_{2})$ passant par $C\;,\ D.$
Exercice 3 BFEM 2006
Soit l'application $f$ définie par : $$f(x)=|x+3|$$
1) Calculons : $f(0)\ $ et $\ f(-3).$
Dans l'expression de $f(x)$, en remplaçant $x$ par $0$, on obtient :
$\begin{array}{rcl} f(0)&=&|0+3|\\\\&=&|3|\\\\&=&3\end{array}$
Donc, $\boxed{f(0)=3}$
Dans l'expression de $f(x)$, en remplaçant $x$ par $-3$, on obtient :
$\begin{array}{rcl} f(-3)&=&|-3+3|\\\\&=&|0|\\\\&=&0\end{array}$
Donc, $\boxed{f(-3)=0}$
2) Montrons que $f$ est une application affine par intervalle.
Soit : $f(x)=|x+3|$
Étudions le signe de $(x+3).$
On a : $x+3=0$ si, et seulement si, $x=-3$
Donc, $(x+3)$ est positif pour tout $x>-3$ et négatif pour $x<-3.$
Regroupant alors ces informations dans le tableau de signes suivant :
$$\begin{array}{|c|lcccr|}\hline x&-\infty& &-3& &+\infty \\ \hline\text{signe de }(x+3)& &-&|&+& \\ \hline f(x)& &-(x+3)&0&(x+3)& \\ \hline\end{array}$$
Donc,
$-\ $ si $x\in\;]-\infty\;;\ -3]\;,\quad f(x)=-x-3$
$-\ $ si $x\in\;[-3\;;\ +\infty[\;,\quad f(x)=x+3$
Par conséquent, $f$ est une application affine par intervalle.
3) Représentons graphiquement $f$ dans un repère orthonormé $(O\;,\ I\;,\ J).$
Pour cela, traçons les deux droites suivantes :
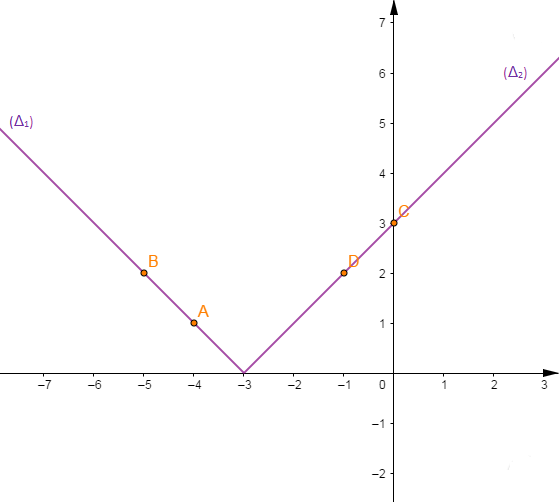
$(\Delta_{1})\ :\ y=-x-3\ $ pour $x\in\;]-\infty\;;\ -3]$
$(\Delta_{2})\ :\ y=x+3\ $ pour $x\in\;[-3\;;\ +\infty[$
Choisissons alors $A\;,\ B\in(\Delta_{1})\ $ et $\ C\;,\ D\in(\Delta_{2})$
Soit :
$$\begin{array}{|c|c|c|}\hline&A&B \\ \hline x&-4&-5 \\ \hline y&1&2 \\ \hline \end{array}\qquad\qquad \begin{array}{|c|c|c|}\hline&C&D \\ \hline x&0&-1 \\ \hline y&3&2 \\ \hline\end{array}$$
Traçons alors la droite $(\Delta_{1})$ passant par $A\;,\ B\ $ et la droite $(\Delta_{2})$ passant par $C\;,\ D.$
4) Résolvons dans $\mathbb{R}$ l'équation $f(x)=1.$
On a : $f(x)=1$ si, et seulement si, $|x+3|=1.$
Résolvons alors l'équation $|x+3|=1.$
En utilisant la propriété de la valeur absolue, on a :
$\begin{array}{rcl}\left|x+3\right|=1&\Leftrightarrow&x+3=1\ \text{ ou }\ x+3=-1\\\\&\Leftrightarrow&x=1-3\ \text{ ou }\ x=-1-3\\\\&\Leftrightarrow&x=-2\ \text{ ou }\ x=-4\end{array}$
Donc, $|x+3|=1$ si, et seulement si, $x=-2\ $ ou $\ x=-4$
D'où, l'équation $f(x)=1$ a pour solution dans $\mathbb{R}\ :$
$$S=\{-4\;;\ -2\}$$
Exercice 4
1) Résolvons dans $\mathbb{R}\times\mathbb{R}$ le système d'équation suivant : $$\left\lbrace\begin{array}{rcl} 6x+y-440&=&0\qquad(1)\\ 17x+2y-1080&=&0\qquad(2)\end{array}\right.$$
Dans l'équation (1), en expriment $y$ en fonction de $x$ on obtient : $$y=440-6x\qquad(3)$$
Remplaçons cette expression de $y$ dans l'équation (2).
On a : $17x+2\times(440-6x)-1080=0$
Donc, $17x-12x+880-1080=0\ $ ; c'est-à-dire $5x=200$
D'où, $x=\dfrac{200}{5}=40$
En remplaçant cette valeur de $x$ dans l'équation (3) on obtient :
$y=440-6\times 40=440-240=200$
Ainsi, $$S=\{(40\;;\ 200)\}$$
2) a) Déterminons le prix d'une minute de communication et la somme forfaitaire sur le réseau "EXPRESSO"
Considérons le système de départ et divisons l'équation (2) par $2.$
On obtient : $$\left\lbrace\begin{array}{rcl} 6x+y-440&=&0\\ 8.5x+y-540&=&0\end{array}\right.$$
Ce qui est équivalent à :
$$\left\lbrace\begin{array}{rcl} 6x+y&=&440\qquad(4)\\ 8.5x+y&=&540\qquad(5)\end{array}\right.$$
Choisissons $x$ comme étant le nombre de minutes de communication et $y$ la somme forfaitaire sur le réseau "EXPRESSO" alors, on constate que l'équation (4) représente l'opération de Alioune et l'équation (5) celle de Fatou.
Donc, en résolvant ce système on déterminera $x\ $ et $\ y.$
Or, ce système est équivalent au système de départ dont la solution est donnée par : $$S=\{(40\;;\ 200)\}$$
C'est-à-dire $\ \ x=40\quad$ et $\quad y=200$
Ainsi, le prix d'une minute de communication est égal à $40\;F\,CFA$ et la somme forfaitaire sur le réseau "EXPRESSO" est de $200\;F\,CFA.$
b) Déterminons l'application affine qui définit la somme à payer en fonction du nombre de minute de communication.
Soit $f$ cette application affine.
Déterminons $f$
On a : $f(x)=ax+b$
Or, en prenant le cas de Alioune on a $f(6)=440$ et pour Fatou $f(8.5)=540$
Alors, $a=\dfrac{f(8.5)-f(6)}{8.5-6}=\dfrac{540-440}{2.5}=\dfrac{100}{2.5}=40$
Donc, $f(x)=40x+b$
et comme $f(6)=40\times 6+b\ \ $ et $\ \ f(6)=440$, alors $240+b=440$
Ainsi, $b=440-240=200$
D'où, $\boxed{f(x)=40x+200}$
c) Représentons graphiquement cette application dans un repère orthonormé.
Soit $(D)$ la droite d'équation $y=40x+200.$
Représenter graphiquement $f$ revient tout simplement à représenter $(D).$
Pour cela, choisissons deux points $A$ et $B$ dont les coordonnées vérifient l'équation de $(D).$
On a : $$\begin{array}{|c|c|c|}\hline&A&B \\ \hline x&6&8.5 \\ \hline y&440&540 \\ \hline \end{array}$$
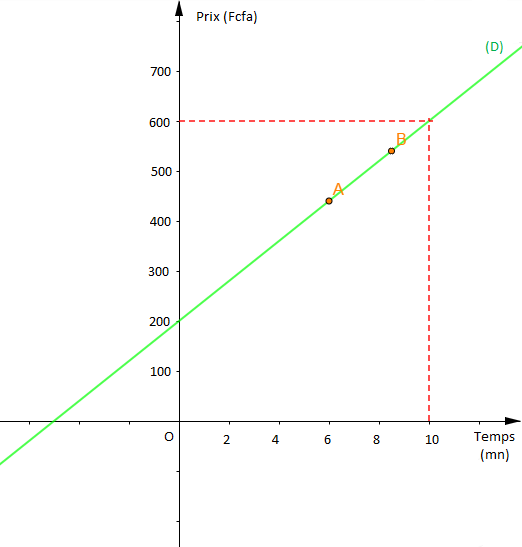
$$\begin{array}{rcl} \text{Echelle }:\ 1\;cm&\longrightarrow&2\;\text{minutes} \\ 1\;cm&\longrightarrow&100\;\text{F CFA}\end{array}$$
d) Déterminons graphiquement la somme à payer pour $10$ minutes de communication.
On projette $x=6$ sur $(D)$ et à partir de $(D)$ on projette sur l'axe des prix.
Ce qui donne $y=600$
Donc, pour $10$ minutes de communication on doit payer $600\;F\,CFA.$
Exercice 5 BFEM 2004
1) Pour organiser une colonie de vacances pour les $50$ enfants de ses employés, une société établie à Dakar lance un appel d'offre auquel $3$ agences de transport $A\;,\ B\ $ et $\ C$ ont soumissionné :
L'agence $A$ réclame pour chacun de ses cars un forfait de $30\,000\;F\ $ et $\ 500\;F$ pour chaque $km.$
L'agence $B$ réclame pour chacun de ses cars un forfait de $40\,000\;F\ $ et $\ 300\;F$ pour chaque $km.$
L'agence $C$ réclame $64\,000\;F$ pour chacun de ses cars.
a) Établissons la relation exprimant la somme $y$ à payer en fonction du nombre $x$ de kilomètres parcourus pour chacune des $3$ agences.
Comme l'agence $A$ réclame pour chacun de ses cars un forfait de $30\,000\;F\ $ et $\ 500\;F$ pour chaque $km$ parcouru alors, la somme $y$ à payer pour $x$ de kilomètres parcourus est donnée par :
$$y=30\,000+500\times x=30\,000+500x$$
Comme l'agence $B$ réclame pour chacun de ses cars un forfait de $40\,000\;F\ $ et $\ 300\;F$ pour chaque $km$ parcouru alors, la somme $y$ à payer pour $x$ de kilomètres parcourus est donnée par :
$$y=40\,000+300\times x=40\,000+300x$$
Comme l'agence $C$ réclame pour chacun de ses cars un forfait de $64\,000\;F\ $ et $\ 0\;F$ pour chaque $km$ parcouru alors, la somme $y$ à payer pour $x$ de kilomètres parcourus est donnée par :
$$y=64\,000+0\times x=64\,000$$
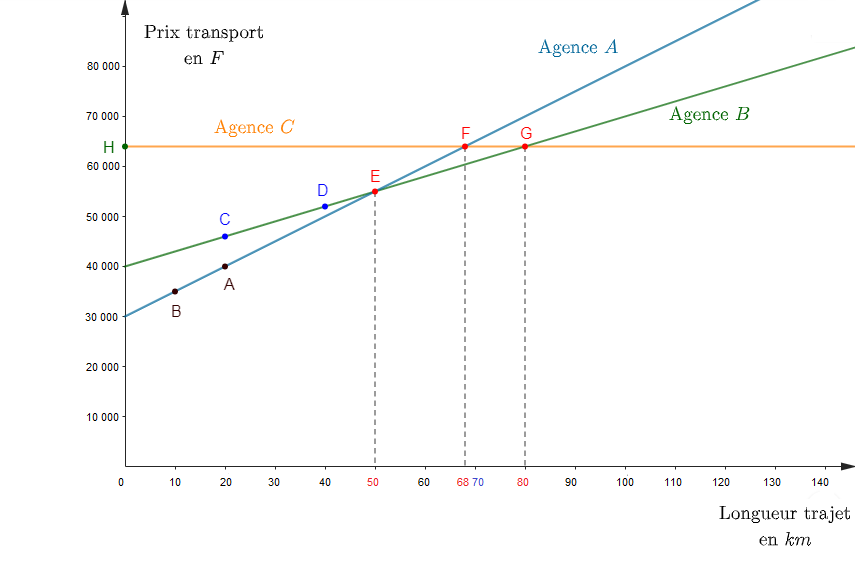
b) Dans un même repère orthonormal ($1\;cm$ pour $10\;km$ en abscisses et $1\;cm$ pour $10\,000\;F$ en ordonnées), représentons graphiquement les $3$ relations précédemment obtenues.
Pour l'agence $A$, nous allons donc tracer la droite d'équation :
$$y=30\,000+500x$$
Choisissons deux points $A\ $ et $\ B$ dont les coordonnées vérifient cette équation.
On a :
$$\begin{array}{|c|c|c|}\hline&A&B \\ \hline x&20&10 \\ \hline y&40\,000&35\,000 \\ \hline \end{array}$$
Ainsi, la droite passant par $A\ $ et $\ B$ représente la somme réclamée par l'agence $A.$
Ensuite, pour l'agence $B$, nous allons tracer la droite d'équation :
$$y=40\,000+300x$$
Choisissons alors deux points $C\ $ et $\ D$ dont les coordonnées vérifient cette équation.
On a :
$$\begin{array}{|c|c|c|}\hline&C&D \\ \hline x&20&40 \\ \hline y&46\,000&52\,000 \\ \hline \end{array}$$
Donc, la droite passant par $C\ $ et $\ D$ représente la somme réclamée par l'agence $B.$
Enfin, pour l'agence $C$, nous allons donc tracer la droite d'équation :
$$y=64\,000$$
C'est la droite passant par le point $H(0\;;\ 64\,000)$ et parallèle à l'axe des abscisses.
Cette droite représente donc la somme réclamée par l'agence $C.$

$$\begin{array}{rcl} \text{Echelle }:\ 1\;cm&\longrightarrow&10\;km \\ 1\;cm&\longrightarrow&10\,000\;\text{F}\end{array}$$
c) Déterminons graphiquement sur quelle longueur de trajet :
$-\ $ L'agence $A$ réclame plus que l'agence $B$
Sur la figure, nous remarquons que les représentations graphiques des agences $A\ $ et $\ B$ se croisent au point $E$ d'abscisse $50.$
Ainsi, lorsque $x$ est supérieur à $50$, la représentation graphique de l'agence $A$ est au dessus de celle de l'agence $B.$
Ce qui signifie que l'agence $A$ réclame plus que l'agence $B$ lorsque $x$ est supérieur à $50.$
Donc, sur une longueur de trajet supérieure à $50\;km$, l'agence $A$ réclame plus que l'agence $B.$
$-\ $ L'agence $A$ et l'agence $C$ réclament la même somme
Sur le graphique, nous constatons que les représentations graphiques des agences $A\ $ et $\ C$ se croisent au point $F$ d'abscisse $68$
Ce qui signifie qu'au point $F$, l'agence $A$ réclame la même somme que l'agence $C.$
Donc, pour $x=68$, l'agence $A$ et l'agence $C$ réclament la même somme.
Ainsi, sur une longueur de trajet égale à $68\;km$, l'agence $A$ et l'agence $C$ réclament la même somme.
$-\ $ L'agence $B$ réclame moins que l'agence $C.$
En observant le graphique, nous remarquons que les représentations graphiques des agences $B\ $ et $\ C$ se coupent au point $G$ d'abscisse $80.$
Ainsi, lorsque $x$ est inférieur à $80$, la représentation graphique de l'agence $B$ est en dessous de la représentation graphique de l'agence $C.$
Ce qui signifie que l'agence $B$ réclame moins que l'agence $C$ lorsque $x$ est inférieur à $80.$
Donc, sur une longueur de trajet inférieure à $80\;km$, l'agence $B$ réclame moins que l'agence $C.$
2) Les enfants sont répartis en deux groupes :
Le $1e$ groupe va à Thiès, ville distante de $70\;km$ de Dakar.
Le $2e$ groupe va à Kaolack, ville distante de $192\;km$ de Dakar.
a) Indiquons sur chacun de ces deux trajets l'agence la moins chère qui sera retenue.
La longueur du trajet Dakar - Thiès est de $70\;km.$
Alors, en observant le graphique, nous constatons que pour $x=70$, la représentation de l'agence $B$ est en dessous de celles des autres agences.
Ce qui signifie que l'agence $B$ est la moins chère et donc sera retenue pour ce trajet.
La longueur du trajet Dakar - Kaolack est égale à $192\;km.$
Alors, sur le graphique, nous remarquons que pour $x>80$, la représentation de l'agence $C$ est en dessous de celles des deux autres.
Or, $192>80$ donc, pour l'abscisse $x=192$, la représentation de l'agence $C$ est en dessous de celles des deux autres.
Ce qui signifie que l'agence $C$ est la moins chère et donc sera retenue pour ce trajet.
Remarque :
Par le calcul direct, on pouvait aussi remplacer $x$ par sa valeur, dans chacune des équations des $3$ agences puis, comparer les valeurs de $y$ obtenues.
Ainsi,
$-\ $ pour le voyage sur Thiès, avec $70\;km$, on aura :
Agence $A\ :\ y=30\,000+500\times 70=30\,000+35\,000=65\,000\;F$
Agence $B\ :\ y=40\,000+300\times 70=40\,000+21\,000=61\,000\;F$
Agence $C\ :\ y=64\,000\;F$
Alors, on constate que l'agence $B$, avec $61\,000\;F$, réclame moins que les autres agences. Par conséquent, elle sera retenue pour ce trajet.
$-\ $ pour le voyage sur Kaolack, avec $192\;km$, on aura :
Agence $A\ :\ y=30\,000+500\times 192=30\,000+96\,000=126\,000\;F$
Agence $B\ :\ y=40\,000+300\times 192=40\,000+57\,600=97\,600\;F$
Agence $C\ :\ y=64\,000\;F$
On constate alors que l'agence $C$, avec $64\,000\;F$, réclame moins que les autres agences. Donc, elle sera retenue pour ce trajet.
b) L'agence $A$ est l'agence qui n'aura aucune part de ce marché.
En effet, l'agence $A$ n'a pas été retenue pour le trajet Dakar - Thiès ainsi que pour le trajet Dakar - Kaolack.
Par conséquent, l'agence $A$ n'aura aucune part de ce marché.
3) Deux cars sont prévus pour le voyage sur Kaolack et cinq cars pour le voyage sur Thiès. Si chacun des enfants du premier groupe verse $5\,000\;F$ et chacun des enfants du deuxième groupe verse $3\,000\;F$ alors, la société devra compléter pour $223\,000\;F$ pour couvrir les frais de transport.
Déterminons le nombre d'enfants qui composent chaque groupe.
Nous appelons $a$ le nombre d'enfants du premier groupe et $b$ le nombre d'enfants du deuxième groupe.
En effet, pour le trajet Dakar - Kaolack, l'agence $C$ a été retenue.
Or, cette agence réclame, pour chacun de ses cars : $y=64\,000\;F$
Comme $2$ cars sont prévus pour le voyage sur Kaolack alors, les frais de transport s'élèvent à :
$$64\,000\;F\times 2=128\,000\;F$$
Pour le trajet Dakar - Thiès, l'agence $B$ a été retenue et cette agence réclame, pour chacun de ses cars :
$\begin{array}{rcl} y&=&40\,000+300x\\\\&=&40\,000+300\times 70\\\\&=&40\,000+21\,000\\\\&=&61\,000\;F\end{array}$
Comme $5$ cars sont prévus pour ce voyage alors, les frais de transports s'élèvent à :
$$61\,000\;F\times 5=305\,000\;F$$
Donc, les frais de transport pour les deux voyages s'élèvent à :
$$128\,000\;F+305\,000\;F=433\,000\;F$$
On sait que : chacun des enfants du premier groupe a versé $5\,000\;F$ et chacun des enfants du deuxième groupe a versé $3\,000\;F$ et la société a complété pour $223\,000\;F$ pour couvrir les frais de transport.
Ce qui se traduit par :
$$5\,000\times a+3\,000\times b+223\,000=433\,000$$
C'est-à-dire ; $5\,000a+3\,000b=433\,000-223\,000$
Ce qui donne : $5\,000a+3\,000b=210\,000$
Ainsi, en simplifiant par $1\,000$, on trouve :
$$5a+3b=210\qquad(\text{équation }1)$$
Par ailleurs, on sait que cette colonie de vacances concerne $50$ enfants donc, cela signifie :
$$a+b=50\qquad(\text{équation }2)$$
On obtient alors un système d'équations composé des équations $(1)\ $ et $\ (2).$
$$\left\lbrace\begin{array}{rclr} 5a+3b&=&210&\quad(1)\\\\a+b&=&50&\quad(2)\end{array}\right.$$
En résolvant ce système, on trouve $a\ $ et $\ b.$
En multipliant l'équation $(2)$ par $-3$, on obtient :
$$-3a-3b=-150\qquad(3)$$
En additionnant membre à membre les équations $(1)\ $ et $\ (3)$, on trouve :
$\begin{array}{rcl} 5a+3b-3a-3b=210-150&\Leftrightarrow&2a=60\\\\&\Leftrightarrow&a=\dfrac{60}{2}\\\\&\Leftrightarrow&a=30\end{array}$
Donc, $\boxed{a=30}$
Remplaçons ensuite cette valeur de $a$ dans l'équation $(2).$
On trouve alors :
$\begin{array}{rcl} a+b=50&\Rightarrow&30+b=50\\\\&\Rightarrow&b=50-30\\\\&\Rightarrow&b=20\end{array}$
Donc, $\boxed{b=20}$
Ainsi, le premier groupe est composé de $30$ enfants et le second groupe de $20$ enfants.
Exercice 6
On définit l'application $f$ dans $\mathbb{R}$ par :
$$f(x)=|2-x|$$
1) Montrons que $f$ est une application affine par intervalle.
Étudions le signe de $(2-x).$
On a : $2-x=0$ si, et seulement si, $x=2$
Or, on remarque que dans l'expression $(2-x)$, le coefficient associé à $x$ est négatif.
Donc, $(2-x)$ est positif pour tout $x<2$ et négatif pour $x>2.$
En regroupant ces informations dans un tableau de signes, on obtient :
$$\begin{array}{|c|lcccr|}\hline x&-\infty& &2& &+\infty \\ \hline\text{signe de }(2-x)& &+&|&-& \\ \hline f(x)& &(2-x)&0&-(2-x)& \\ \hline\end{array}$$
Donc,
$-\ $ si $x\in\;]-\infty\;;\ 2]\;,\quad f(x)=2-x$
$-\ $ si $x\in\;[2\;;\ +\infty[\;,\quad f(x)=x-2$
Par conséquent, $f$ est une application affine par intervalle.
2) Déterminons les variations de $f$ dans les intervalles $]-\infty\;;\ 2]\ $ et $\ [2\;;\ +\infty[.$
$-\ $ Dans l'intervalle $]-\infty\;;\ 2]\;,\ f$ est une application affine définie par :
$$f(x)=2-x$$
Considérons alors l'application linéaire $f_{1}$ associée à $f$ et définie par :
$$f_{1}(x)=-x$$
On constate que le coefficient linéaire de $f_{1}$ est négatif.
Donc, $f$ est décroissante dans l'intervalle $]-\infty\;;\ 2].$
$-\ $ Dans l'intervalle $[2\;;\ +\infty[\;,\ f$ est une application affine définie par :
$$f(x)=x-2$$
Considérons alors $f_{2}$, l'application linéaire associée à $f$ et définie par :
$$f_{2}(x)=x$$
On remarque que le coefficient linéaire de $f_{2}$ est positif.
Par conséquent, $f$ est croissante dans l'intervalle $[2\;;\ +\infty[.$
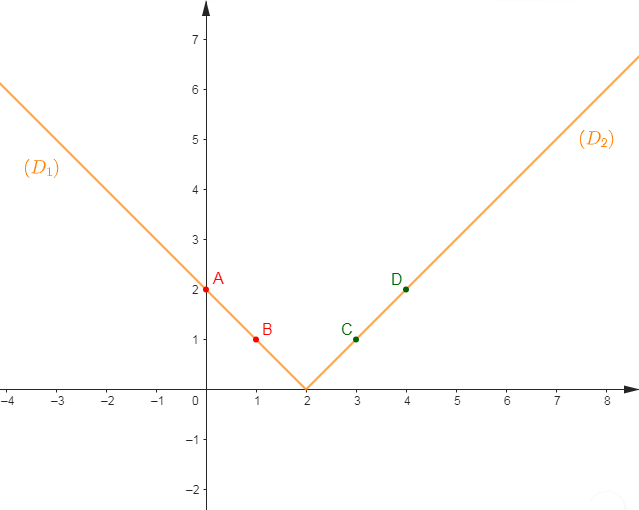
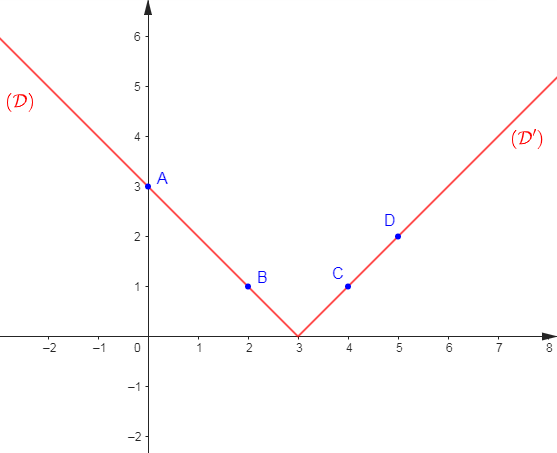
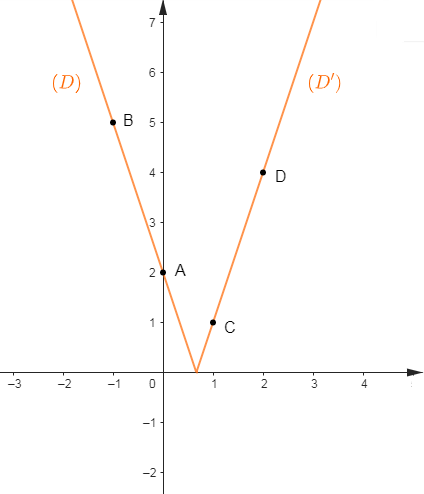
3) Représentons $f$ dans un repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j}).$
Pour cela, représentons les droites :
$(D_{1})\ :\ y=2-x$ dans l'intervalle $\left]-\infty\;;\ 2\right]$
$(D_{2})\ :\ y=x-2$ dans l'intervalle $\left[2\;;\ +\infty\right[$
Choisissons alors deux points $A\;,\ B$ appartenant à $(D_{1})$ et deux points $C\;,\ D$ appartenant à $(D_{2}).$
Soit :
$$\begin{array}{|c|c|c|}\hline&A&B \\ \hline x&0&1 \\ \hline y&2&1 \\ \hline \end{array}\qquad\qquad \begin{array}{|c|c|c|}\hline&C&D \\ \hline x&3&4 \\ \hline y&1&2 \\ \hline\end{array}$$
Traçons alors la droite $(D_{1})$ passant par $A\;,\ B\ $ et la droite $(D_{2})$ passant par $C\;,\ D.$

Exercice 7
On considère l'application affine $g$ telle que $g(-1)=4\ $ et $\ g(-2)=0.$
1) Déterminons l'expression littérale de $g.$
Comme $g$ est une application affine définie dans $\mathbb{R}$ alors, $g$ est de la forme :
$$g(x)=ax+b$$
avec $a$ son coefficient directeur et $b$ son ordonnée à l'origine.
Or, on sait que : $g(-1)=4\ $ et $\ g(-2)=0.$
Donc, le coefficient directeur $a$ est donné par :
$\begin{array}{rcl} a&=&\dfrac{g(-1)-g(-2)}{(-1)-(-2)}\\\\&=&\dfrac{4-0}{-1+2}\\\\&=&\dfrac{4}{1}\\\\&=&4\end{array}$
Donc, $g(x)=4x+b$
Ensuite, on détermine $b$ en calculant $g(-1)\ $ ou $\ g(-2)$ à partir de l'expression de $g(x).$
Soit : $g(-2)=4\times(-2)+b=-8+b$
Or, $g(-2)=0$ donc, $-8+b=0$
C'est-à-dire ; $b=8$
Ainsi, $\boxed{g(x)=4x+8}$
2) En déduisons $g'$ l'application linéaire associée à $g(x).$
$g(x)=4x+8$ étant une application affine alors, $g'$ l'application linéaire associée à $g(x)$ est donnée par :
$$g'(x)=4x$$
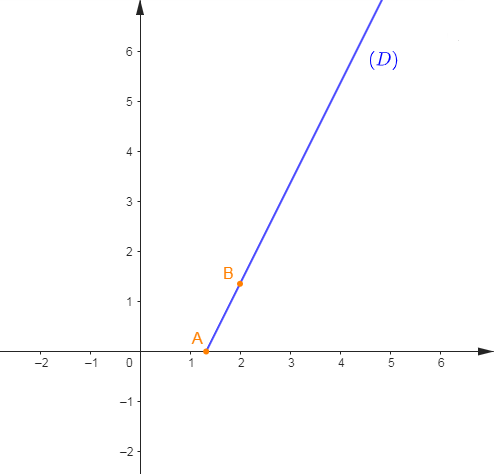
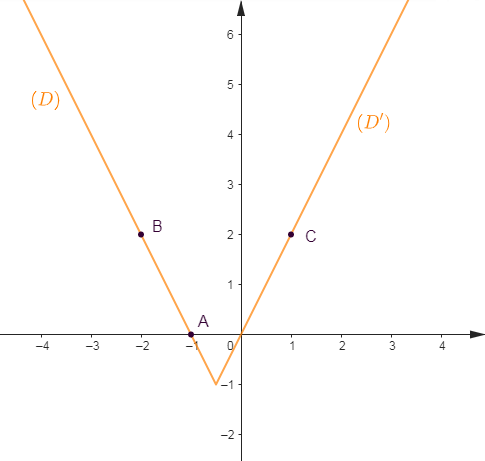
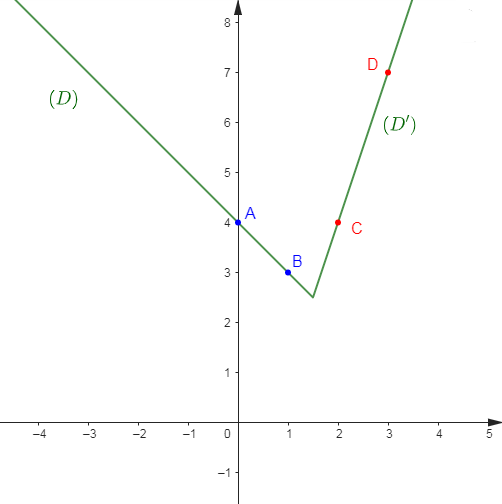
3) Représentons $g(x)\ $ et $\ g'(x)$ puis, déduisons-en la position relative des deux représentations.
Pour cela, on représente les droites :
$(\mathcal{D})\ :\ y=4x+8$
$(\mathcal{D}')\ :\ y=4x$
Choisissons alors deux points $A\;,\ B$ appartenant à $(\mathcal{D})$ et un point $C$ appartenant à $(\mathcal{D}').$
Soit :
$$\begin{array}{|c|c|c|}\hline&A&B \\ \hline x&-1&-2 \\ \hline y&4&0 \\ \hline \end{array}\qquad\qquad \begin{array}{|c|c|}\hline&C \\ \hline x&1 \\ \hline y&4 \\ \hline\end{array}$$
Traçons alors la droite $(\mathcal{D})$ passant par $A\;,\ B\ $ et la droite $(\mathcal{D}')$ passant par $C$ et par le point $O$ origine du repère.
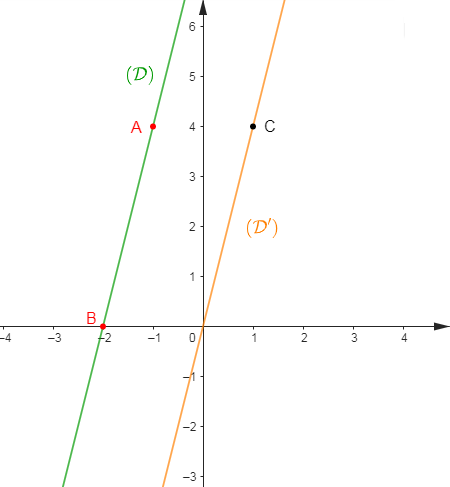
Les droites $(\mathcal{D})\ $ et $\ (\mathcal{D}')$ sont parallèles.
Exercice 8
On considère la fonction affine suivante :
$$f(x)=|x+1|-2$$
1) Écrivons $f(x)$ sans la valeur absolue.
Pour cela, déterminons d'abord le signe de $(x+1).$
On a : $x+1=0$ si, et seulement si, $x=-1$
Donc, $(x+1)$ est positif pour tout $x>-1$ et négatif pour $x<-1.$
Alors, en regroupant ces informations dans un tableau de signes, on obtient :
$$\begin{array}{|c|lcccr|}\hline x&-\infty& &-1& &+\infty \\ \hline\text{signe de }(x+1)& &-&|&+& \\ \hline |x+1|& &-x-1&0&x+1& \\ \hline\end{array}$$
Donc,
$-\ $ dans l'intervalle $]-\infty\;;\ -1]$, en remplaçant $|x+1|$ par $-x-1$, on obtient :
$$f(x)=-x-1-2=-x-3$$
$-\ $ dans l'intervalle $[-1\;;\ +\infty[$, en remplaçant $|x+1|$ par $x+1$, on obtient :
$$f(x)=x+1-2=x-1$$
2) En déduisons que $f$ est une application affine par intervalles et précisons ses intervalles de définition.
D'après le résultat de la question $1)$, on a :
$f(x)=-x-3$ si $x$ appartient à l'intervalle $]-\infty\;;\ -1]$
$f(x)=x-1$ si $x$ appartient à l'intervalle $[-1\;;\ +\infty[$
Par conséquent, $f$ est une application affine par intervalle.
Ses intervalles de définition sont : $]-\infty\;;\ -1]\ $ et $\ [-1\;;\ +\infty[$
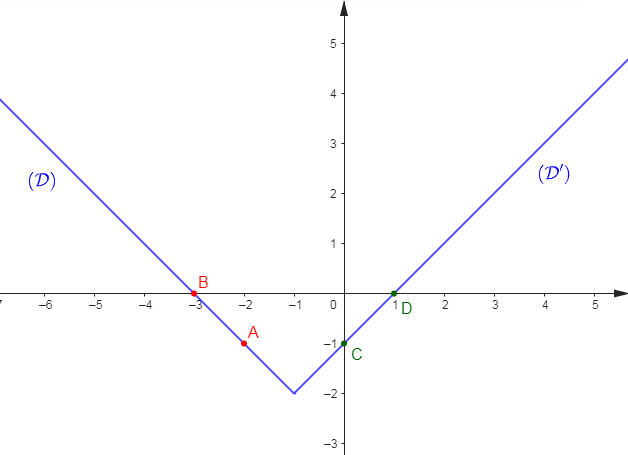
3) Représentons $f$ dans un repère orthonormal.
Pour cela, nous allons représenter les droites :
$(\mathcal{D})\ :\ y=-x-3$ dans l'intervalle $\left]-\infty\;;\ -1\right]$
$(\mathcal{D}')\ :\ y=x-1$ dans l'intervalle $\left[-1\;;\ +\infty\right[$
Choisissons d'abord deux points $A\;,\ B$ appartenant à $(\mathcal{D})$ et deux points $C\;,\ D$ appartenant à $(\mathcal{D}').$
Soit :
$$\begin{array}{|c|c|c|}\hline&A&B \\ \hline x&-2&-3 \\ \hline y&-1&0 \\ \hline \end{array}\qquad\qquad \begin{array}{|c|c|c|}\hline&C&D \\ \hline x&0&1 \\ \hline y&-1&0 \\ \hline\end{array}$$
Traçons ensuite la droite $(\mathcal{D})$ passant par $A\;,\ B\ $ et la droite $(\mathcal{D}')$ passant par $C\;,\ D.$
C'est la représentation de $f.$

Exercice 9
Le plan est muni d'un repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j}).$
a) Trouvons l'application affine $f$ dont la représentation graphique est la droite $(D)$ passant par les points $A(-1\;;\ 2)\ $ et $\ B(\sqrt{3}\;;\ 0).$
Comme $f$ est une application affine définie dans $\mathbb{R}$ alors, $f$ est de la forme :
$$f(x)=ax+b$$
avec $a$ son coefficient directeur et $b$ son ordonnée à l'origine.
Or, on sait que : la représentation graphique de $f$ est la droite $(D)$ passant par les points $A(-1\;;\ 2)\ $ et $\ B(\sqrt{3}\;;\ 0).$
Ce qui signifie que : $f(-1)=2\ $ et $\ f(\sqrt{3})=0.$
Ainsi, le coefficient directeur $a$ de $f$ est donné par :
$\begin{array}{rcl} a&=&\dfrac{f(-1)-f(\sqrt{3})}{(-1)-(\sqrt{3})}\\\\&=&\dfrac{2-0}{-1-\sqrt{3}}\\\\&=&\dfrac{2}{-1-\sqrt{3}}\end{array}$
Donc, $a=\dfrac{2}{-1-\sqrt{3}}$
En rendant rationnel le dénominateur de $a$, on obtient :
$\begin{array}{rcl}\dfrac{2}{-1-\sqrt{3}}&=&\dfrac{2(-1+\sqrt{3})}{(-1-\sqrt{3})(-1+\sqrt{3})}\\\\&=&\dfrac{-2+2\sqrt{3}}{(-1)^{2}-(\sqrt{3})^{2}}\\\\&=&\dfrac{-2+2\sqrt{3}}{1-3}\\\\&=&\dfrac{-2+2\sqrt{3}}{-2}\\\\&=&1-\sqrt{3}\end{array}$
Alors, $a=1-\sqrt{3}$
Donc, $f(x)=(1-\sqrt{3})x+b$
Ensuite, on détermine $b$ en calculant $f(-1)\ $ ou $\ f(\sqrt{3})$ à partir de l'expression de $f(x).$
Soit : $f(\sqrt{3})=(1-\sqrt{3})\times(\sqrt{3})+b=\sqrt{3}-3+b$
Or, $f(\sqrt{3})=0$ donc, $\sqrt{3}-3+b=0$
Par suite, $b=3-\sqrt{3}$
Ainsi, $\boxed{f(x)=(1-\sqrt{3})x+3-\sqrt{3}}$
b) Déterminons le sens de variation de $f.$
En effet, $f$ étant une application affine alors, $f_{1}$ l'application linéaire associée à $f$ est donnée par :
$$f_{1}(x)=(1-\sqrt{3})x$$
Déterminons alors le signe de $(1-\sqrt{3})$ ; coefficient linéaire de $f_{1}.$
Pour cela, comparons $1\ $ et $\ \sqrt{3}.$
On a : $1>0\ $ et $\ \sqrt{3}>0$
Alors, $1^{2}=1\ $ et $\ (\sqrt{3})^{2}=3$
Or, $1<3$ donc, $1<\sqrt{3}$
D'où, $(1-\sqrt{3})<0$
Ainsi, le coefficient linéaire de $f_{1}$ est négatif.
Par conséquent, $f$ est décroissante.

Exercice 10
Soit $P=\sqrt{(\sqrt{2}-3)^{2}}-\sqrt{(3-2\sqrt{2})^{2}}$
1) Calculons $P.$
En effet, on a :
$\sqrt{(\sqrt{2}-3)^{2}}=\left|\sqrt{2}-3\right|$
$\sqrt{(3-2\sqrt{2})^{2}}=\left|3-2\sqrt{2}\right|$
Donc, $P=\left|\sqrt{2}-3\right|-\left|3-2\sqrt{2}\right|$
Écrivons alors $P$ sans les symboles de valeur absolue.
Pour cela, déterminons le signe de $(\sqrt{2}-3)\ $ et $\ (3-2\sqrt{2})$
On a : $\sqrt{2}>0\ $ et $\ 3>0$
Alors, $(\sqrt{2})^{2}=2\ $ et $\ 3^{2}=9$
Or, $2<9$ donc, $\sqrt{2}<3$
D'où, $(\sqrt{2}-3)<0$
Par suite, $\left|\sqrt{2}-3\right|=-(\sqrt{2}-3)=-\sqrt{2}+3$
De la même manière, on a : $3>0\ $ et $\ 2\sqrt{2}>0$
Alors, $3^{2}=9\ $ et $\ (2\sqrt{2})^{2}=8$
Or, $9>8$ donc, $3>2\sqrt{2}$
D'où, $(3-2\sqrt{2})>0$
Par conséquent, $\left|3-2\sqrt{2}\right|=3-2\sqrt{2}$
Ainsi,
$\begin{array}{rcl} P&=&\left|\sqrt{2}-3\right|-\left|3-2\sqrt{2}\right|\\\\&=&(-\sqrt{2}+3)-(3-2\sqrt{2})\\\\&=&-\sqrt{2}+3-3+2\sqrt{2}\\\\&=&\sqrt{2}\end{array}$
D'où, $\boxed{P=\sqrt{2}}$
2) Soit $g(x)=|2x-\sqrt{7}|$
a) Montrons que $g$ est une application affine par intervalles.
Écrivons alors $g(x)$ sans le symbole de la valeur absolue.
Pour cela, étudions le signe de $(2x-\sqrt{7}).$
On a : $2x-\sqrt{7}=0$ si, et seulement si, $2x=\sqrt{7}$
Ce qui donne : $x=\dfrac{\sqrt{7}}{2}$
Donc, $(2x-\sqrt{7})$ est positif pour tout $x>\dfrac{\sqrt{7}}{2}$ et négatif pour $x<\dfrac{\sqrt{7}}{2}.$
En regroupant ces informations dans un tableau de signes, on obtient :
$$\begin{array}{|c|lcccr|}\hline x&-\infty& &\sqrt{7}/2& &+\infty \\ \hline\text{signe de }(2x-\sqrt{7})& &-&|&+& \\ \hline g(x)& &-(2x-\sqrt{7})&0&(2x-\sqrt{7})& \\ \hline\end{array}$$
Donc,
$-\ $ si $x\in\;\left]-\infty\;;\ \dfrac{\sqrt{7}}{2}\right]$ alors, $g(x)=-2x+\sqrt{7}$
$-\ $ si $x\in\;\left[\dfrac{\sqrt{7}}{2}\;;\ +\infty\right[$ alors, $g(x)=2x-\sqrt{7}$
Par conséquent, $g$ est une application affine par intervalle.
b) Déterminons le sens de variation de $g(x)$ dans l'intervalle $\left]-\infty\;;\ \dfrac{\sqrt{7}}{2}\right].$
Dans l'intervalle $\left]-\infty\;;\ \dfrac{\sqrt{7}}{2}\right]$, on a :
$$g(x)=-2x+\sqrt{7}$$
Par suite, l'application linéaire $g_{1}$ associée à $g$, dans cet intervalle, est donnée par :
$$g_{1}(x)=-2x$$
On remarque alors que le coefficient linéaire de $g_{1}$ est négatif.
Par conséquent, $g$ est décroissante dans l'intervalle $\left]-\infty\;;\ \dfrac{\sqrt{7}}{2}\right].$
c) Représentons graphiquement $g(x)$ dans l'intervalle $\left[\dfrac{\sqrt{7}}{2}\;;\ +\infty\right[.$
Dans l'intervalle $\left[\dfrac{\sqrt{7}}{2}\;;\ +\infty\right[$, on a :
$$g(x)=2x-\sqrt{7}$$
Nous allons donc représenter la droite $(D)$ d'équation $y=2x-\sqrt{7}$, dans l'intervalle $\left[\dfrac{\sqrt{7}}{2}\;;\ +\infty\right[.$
Choisissons d'abord deux points $A\;,\ B$ appartenant à $(D)$
On a :
$$\begin{array}{|c|c|c|}\hline&A&B \\ \hline x&\dfrac{\sqrt{7}}{2}&2 \\ \hline y&0&4-\sqrt{7} \\ \hline \end{array}$$
Traçons ensuite la droite $(D)$ passant par $A\;,\ B$ ou tout simplement la demi-droite $[AB).$
C'est la représentation de $g$, dans l'intervalle $\left[\dfrac{\sqrt{7}}{2}\;;\ +\infty\right[.$

Exercice 11
Soit l'application $f$ définie par $f(x)=x^{2}+bx+c$ avec $f(0)=9\ $ et $\ f(-1)=16$
1) Déterminons les réels $b\ $ et $\ c.$
On a : $f(0)=9$
Ce qui signifie : $0^{2}+b\times 0+c=9$
Ce qui donne : $\boxed{c=9}$
De même, on a : $f(-1)=16$
C'est-à-dire ; $(-1)^{2}+b\times(-1)+c=16$
Or, $c=9$ donc, on trouve : $1-b+9=16$
Ce qui donne : $-b=16-10=6$
D'où, $\boxed{b=-6}$
2) Montrons que $f(x)$ est le carré d'un facteur.
En remplaçant $b\ $ et $\ c$ par leur valeur, dans l'expression de $f(x)$, on obtient :
$$f(x)=x^{2}-6x+9$$
Alors, en utilisant une forme factorisée des identités remarquable, on trouve :
$$x^{2}-6x+9=(x-3)^{2}$$
D'où, $\boxed{f(x)=(x-3)^{2}}$
3) Soit $h(x)=\sqrt{(x-3)^{2}}$
a) Montrons que $h$ est une application affine par intervalles.
En effet, on sait que : $\sqrt{(x-3)^{2}}=\left|x-3\right|$
Donc, $h(x)=\left|x-3\right|$
Écrivons alors $h(x)$ sans le symbole de la valeur absolue.
Pour cela, étudions d'abord le signe de $(x-3).$
On a : $x-3=0$ si, et seulement si, $x=3$
Donc, $(x-3)$ est positif pour tout $x>3$ et négatif pour $x<3.$
Regroupons ensuite ces informations dans un tableau de signes.
On obtient :
$$\begin{array}{|c|lcccr|}\hline x&-\infty& &3& &+\infty \\ \hline\text{signe de }(x-3)& &-&|&+& \\ \hline h(x)& &-(x-3)&0&(x-3)& \\ \hline\end{array}$$
Donc,
$-\ $ si $x\in\;\left]-\infty\;;\ 3\right]$ alors, $h(x)=-x+3$
$-\ $ si $x\in\;\left[3\;;\ +\infty\right[$ alors, $h(x)=x-3$
Par conséquent, $h$ est une application affine par intervalle.
b) Représentons graphiquement $h(x)$.
Pour cela, nous allons représenter les droites :
$(\mathcal{D})\ :\ y=-x+3$ dans l'intervalle $\left]-\infty\;;\ 3\right]$
$(\mathcal{D}')\ :\ y=x-3$ dans l'intervalle $\left[3\;;\ +\infty\right[$
Choisissons d'abord deux points $A\;,\ B$ appartenant à $(\mathcal{D})$ et deux points $C\;,\ D$ appartenant à $(\mathcal{D}').$
Soit :
$$\begin{array}{|c|c|c|}\hline&A&B \\ \hline x&0&2 \\ \hline y&3&1 \\ \hline \end{array}\qquad\qquad \begin{array}{|c|c|c|}\hline&C&D \\ \hline x&4&5 \\ \hline y&1&2 \\ \hline\end{array}$$
Traçons ensuite la droite $(\mathcal{D})$ passant par $A\;,\ B\ $ et la droite $(\mathcal{D}')$ passant par $C\;,\ D.$

Exercice 12
Un gérant de cybercafé propose à ses clients deux types d'options :
Optons $I\ :\ 150\;F$ par heure de connexion internet avec un abonnement de $3\,000\;F.$
Option $II\ :\ 350\;F$ par heure de connexion internet sans abonnement
1) Une personne a effectué une connexion mensuelle de $x$ heures.
On note : $P_{1}(x)\ $ et $\ P_{2}(x)$ les prix en francs correspondant respectivement aux options $I\ $ et $\ II.$
Exprimons $P_{1}(x)\ $ et $\ P_{2}(x)$ en fonction de $x.$
$-\ $ Pour l'option $I$, le client paye $150\;F$ pour chaque heure de connexion.
Donc, $x$ heures de connexion vont lui coûter $150\times x=150x.$
De plus, il doit ajouter un abonnement de $3\,000\;F.$
Par conséquent, le prix total $p_{1}(x)$ à payer pour cette option est donné par :
$$p_{1}(x)=150x+3\,000$$
$-\ $ Pour l'option $II$, le client paye $350\;F$ pour chaque heure de connexion.
Donc, pour $x$ heures de connexion, il doit payer $350\times x=350x.$
D'où, le prix total $p_{2}(x)$ à payer pour l'option $II$ est donné par :
$$p_{2}(x)=350x$$
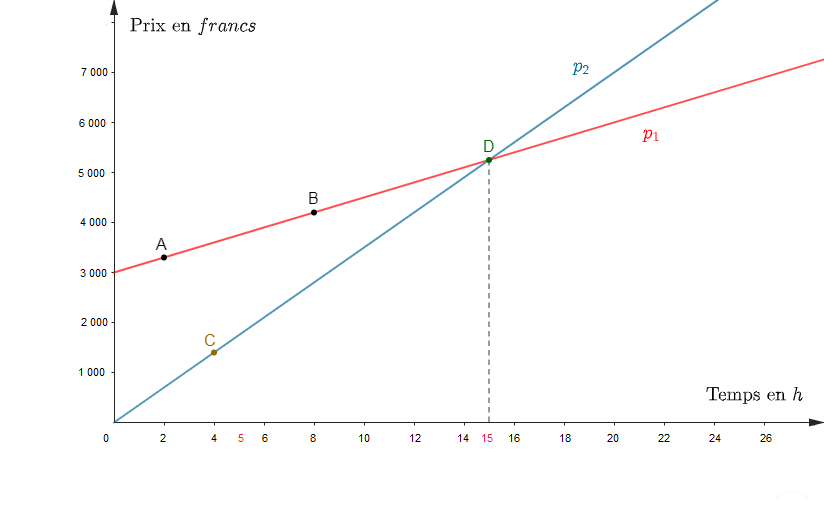
2) Dans un même repère $(O\;;\ \vec{i}\;,\ \vec{j})$, construisons les représentions graphiques des applications affines $p_{1}\ $ et $\ p_{2}.$
Pour la représentation graphique de $p_{1}$, nous allons tracer la droite d'équation :
$$y=150x+3\,000$$
Choisissons deux $A\ $ et $\ B$ dont les coordonnées vérifient cette équation.
On a :
$$\begin{array}{|c|c|c|}\hline&A&B \\ \hline x&2&8 \\ \hline y&3\,300&4\,200 \\ \hline \end{array}$$
Donc, la droite passant par $A\ $ et $\ B$ est la représentation graphique de $p_{1}.$
Pour la représentation graphique de $p_{2}$, nous allons tracer la droite d'équation :
$$y=350x$$
Comme c'est une application linéaire alors, cette droite passe par l'origine $O$ du repère.
Choisissons un point $C$ dont les coordonnées vérifient cette équation.
On a :
$$\begin{array}{|c|c|}\hline&C \\ \hline x&4 \\ \hline y&1\,400 \\ \hline \end{array}$$
Alors, la droite passant par le point $C$ et par l'origine $O$ du repère est la représentation graphique de $p_{2}.$

$$\begin{array}{rcl} \text{Echelle }:\ 1\;cm&\longrightarrow&2\;h \\ 1\;cm&\longrightarrow&1\,000\;\text{F}\end{array}$$
3) a) Déterminons graphiquement dans quel intervalle de temps l'option $I$ est plus avantageuse que l'option $II.$
En observant le graphique, nous constatons que les représentations de $p_{1}\ $ et $\ p_{2}$ se croisent au point $D$ d'abscisse $15.$
Ainsi, lorsque $x$ est supérieur à $15$, la représentation graphique de $p_{1}$ est en dessous de celle de $p_{2}.$
Ce qui signifie que le prix $p_{1}(x)$ est inférieur au prix $p_{2}(x)$ pour tout $x>15\,h.$
Par conséquent, l'option $I$ est plus avantageuse que l'option $II$, lorsque le temps de connexion est supérieur à $15\;h.$
D'où, l'intervalle de temps dans lequel l'option $I$ est plus avantageuse que l'option $II$ est donné par :
$$]15\;;\ +\infty[$$
b) Retrouvons cet intervalle par le calcul.
En effet, on sait que l'option $I$ est plus avantageuse que l'option $II$, lorsque le prix $p_{1}(x)$ est inférieur au prix $p_{2}(x).$
Or, $p_{1}(x)<p_{2}(x)$ si, et seulement si, $150x+3\,000<350x$
En résolvant cette inéquation, on obtient :
$\begin{array}{rcl} 150x+3\,000<350x&\Leftrightarrow&150x-350x<-3\,000\\\\&\Leftrightarrow&-200x<-3\,000\\\\&\Leftrightarrow&x>\dfrac{-3\,000}{-200}\\\\&\Leftrightarrow&x>15\end{array}$
Donc, $p_{1}(x)<p_{2}(x)$ si, et seulement si, $x\in\;]15\;;\ +\infty[$
Ce qui signifie que l'intervalle de temps dans lequel l'option $I$ est plus avantageuse que l'option $II$ est :
$$]15\;;\ +\infty[$$
4) Déterminons le temps de connexion au bout duquel deux clients d'options différentes payeront le même prix.
En effet, deux clients d'options différentes payent le même prix si, et seulement si, $p_{1}(x)=p_{2}(x).$
On a : $p_{1}(x)=p_{2}(x)$ si, et seulement si, $150x+3\,000=350x$
En résolvant cette inéquation, on obtient :
$\begin{array}{rcl} 150x+3\,000=350x&\Leftrightarrow&150x-350x=-3\,000\\\\&\Leftrightarrow&-200x=-3\,000\\\\&\Leftrightarrow&x=\dfrac{-3\,000}{-200}\\\\&\Leftrightarrow&x=15\end{array}$
Donc, $\boxed{x=15}$
Ainsi, au bout de $15\;h$ de connexion, deux clients d'options différentes payeront le même prix.
Autre méthode :
En observant le graphique, nous remarquons que les représentations de $p_{1}\ $ et $\ p_{2}$ se coupent au point $D$ d'abscisse $15.$
Ainsi, lorsque $x=15$, les prix $p_{1}(x)\ $ et $\ p_{2}(x)$ sont les mêmes.
Ce qui signifie deux clients d'options différentes payeront le même prix, au bout de $15\;h$ de connexion.
5) Déterminons l'option la plus avantageuse pour $5\;h$ de connexion.
Pour cela, nous calculons, pour chaque option, le prix à payer, pour $5\;h$ de connexion.
On a :
$p_{1}(5)=150\times 5+3\,000=750+3\,000=3\,750$
$p_{2}(5)=350\times 5=1\,750$
On constate alors que $p_{2}(5)<p_{1}(5).$
D'où, l'option $II$ est plus avantageuse que l'option $I$, pour $5\;h$ de connexion.
$f(0)-f(-1)\ $ et $\ 0-(-1)$ sont de signes contraires.
Or, $0-(-1)=0+1=1$ est positif. Donc, $f(0)-f(-1)$ est négatif.
Exercice 13 BFEM 2009
Soit l'application affine $f$ définie par $f(1)=-1\ $ et $\ f(2)=-3$
1) Montrons que $f(x)=-2x+1$
Comme $f$ est une application affine alors, $f$ est de la forme :
$$f(x)=ax+b$$
avec $a$ son coefficient et $b$ son ordonnée à l'origine.
On a : $f(1)=-1\ $ et $\ f(2)=-3$
Alors, le coefficient $a$ est donné par :
$\begin{array}{rcl} a&=&\dfrac{f(2)-f(1)}{2-1}\\\\&=&\dfrac{-3-(-1)}{1}\\\\&=&-3+1\\\\&=&-2\end{array}$
Donc, $\boxed{a=-2}$
Ainsi, $f(x)=-2x+b$
Pour déterminer $b$, on calcule $f(1).$
On a : $f(1)=-2\times 1+b=-2+b$
Or, $f(1)=-1$ donc, $-2+b=-1$
C'est-à-dire ; $b=-1+2=1$
Donc, $\boxed{b=1}$
Par suite,
$$f(x)=-2x+1$$
2) a) Soit $a\ $ et $\ b$ deux nombres réels distincts. Montrer que $f(a)-f(b)\ $ et $\ a-b$ sont de signes contraires.
En effet, comme $f$ est une application affine de coefficient $-2$ alors, pour tout nombres réels $a\ $ et $\ b$ distincts :
$$\dfrac{f(a)-f(b)}{a-b}=-2$$
Or, $-2<0$ donc, le rapport $\dfrac{f(a)-f(b)}{a-b}<0$
Par conséquent, $f(a)-f(b)\ $ et $\ a-b$ sont de signes contraires.
b) En déduisons que $f(\sqrt{2})<f(0)\ $ et $\ f(0)<f(-1)$
En appliquant le résultat de la question $2)a)$, on a :
$f(\sqrt{2})-f(0)\ $ et $\ \sqrt{2}-0$ sont de signes contraires.
Or, $\sqrt{2}-0=\sqrt{2}$ est positif.
Par suite, $f(\sqrt{2})-f(0)$ est négatif.
Ce qui s'écrit : $f(\sqrt{2})-f(0)<0$
D'où, $f(\sqrt{2})<f(0)$
De la même manière, on a :
$f(0)-f(-1)\ $ et $\ 0-(-1)$ sont de signes contraires.
Or, $0-(-1)=0+1=1$ est positif. Donc, $f(0)-f(-1)$ est négatif.
Ce qui s'écrit : $f(0)-f(-1)<0$
Par conséquent, $f(0)<f(-1)$
3) Le plan est muni d'un repère orthonormal.
$(D)$ est la droite d'équation $y=-2x+1\ $ et $\ (D')$ est la droite d'équation $y+x=0.$
a) Montrons que $(D)\ $ et $\ (D')$ sont sécantes.
En effet, l'équation de droite $(D')$ peut encore s'écrire : $y=-x.$
Ainsi :
$(D)$ a pour coefficient directeur $-2$
$(D')$ a pour coefficient directeur $-1$
On remarque alors que les droites $(D)\ $ et $\ (D')$ n'ont pas le même coefficient directeur.
Ce qui signifie qu'elles ne sont pas parallèles.
Par conséquent, $(D)\ $ et $\ (D')$ sont sécantes.
Par contre, ces deux droites ne sont pas perpendiculaires car, le produit de leur coefficient directeur n'est pas égal à $-1.$
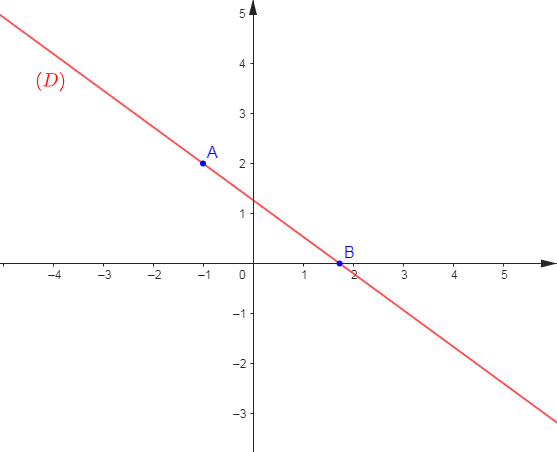
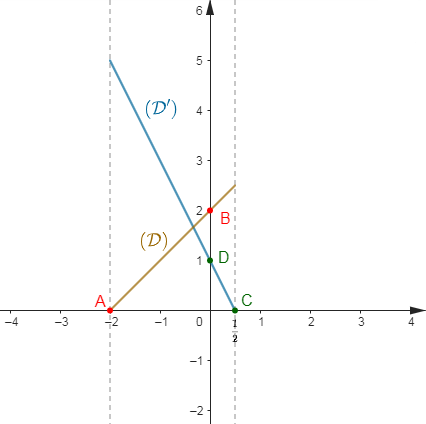
b) Traçons les droites $(D)\ $ et $\ (D')$
On remarque d'abord que $(D')$ est une représentation d'une application linéaire donc, elle passe par l'origine du repère.
Choisissons alors deux points $A\;,\ B$ appartenant à $(D)$ et un point $C$ appartenant à $(D').$
Soit :
$$\begin{array}{|c|c|c|}\hline&A&B \\ \hline x&2&0 \\ \hline y&-3&1 \\ \hline \end{array}\qquad\qquad \begin{array}{|c|c|}\hline&C \\ \hline x&2 \\ \hline y&-2 \\ \hline\end{array}$$
Traçons ensuite la droite $(D)$ passant par $A\;,\ B\ $ et la droite $(D')$ passant par $C$ et par $O$ ; origine du repère.
c) Déterminons le point d'intersection de $(D)\ $ et $\ (D').$
En observant le graphique, nous constatons que les $(D)\ $ et $\ (D')$ se coupent au point $E.$
Alors, en projetant orthogonalement ce point sur les axes du repère, on trouve les coordonnées de $E$ données par :
$$E(1\;;\ -1)$$
Autre méthode :
On peut aussi trouver les coordonnées du point d'intersection de $(D)\ $ et $\ (D')$ en résolvant le système d'équations formé des équations de $(D)\ $ et $\ (D').$
Soit : $\left\lbrace\begin{array}{rcl} y+2x-1&=&0\\\\y+x&=&0\end{array}\right.$
Ce qui est équivalent à : $\left\lbrace\begin{array}{rclr} y+2x-1&=&0&\qquad(1)\\\\y&=&-x&\qquad(2)\end{array}\right.$
Alors, dans l'équation $(1)$, en remplaçant $y$ par $-x$, on obtient :
$\begin{array}{rcl} y+2x-1=0&\Rightarrow&-x+2x-1=0\\\\&\Rightarrow&x-1=0\\\\&\Rightarrow&x=1\end{array}$
Dans l'équation $(2)$, en remplaçant cette valeur de $x$, on trouve : $y=-1$
Ainsi, $\boxed{E(1\;;\ -1)}$
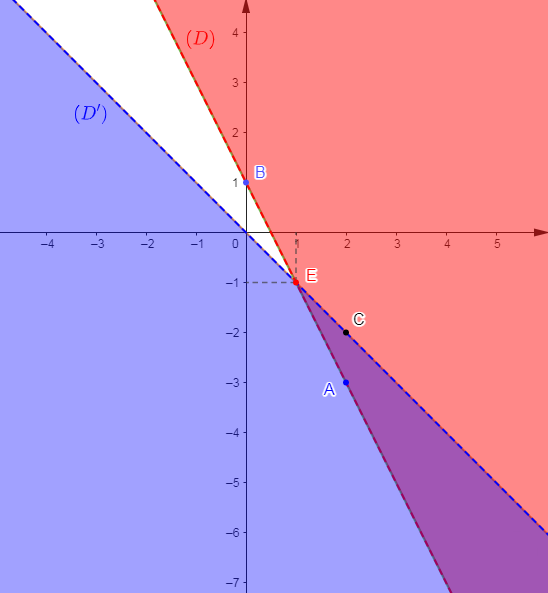
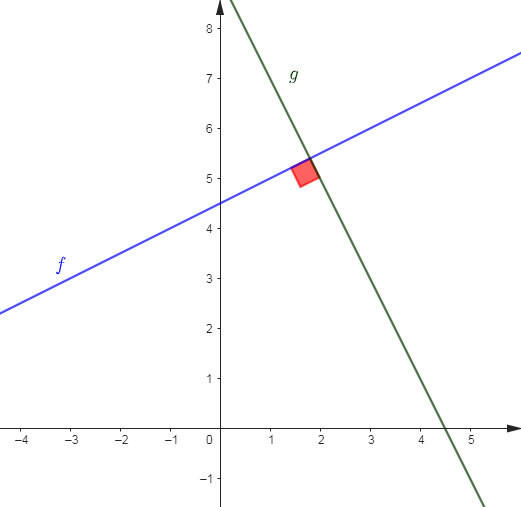
d) Résolvons graphiquement le système :
$$\left\lbrace\begin{array}{rcl} y+2x-1&>&0\\\\y+x&<&0\end{array}\right.$$
Sur le graphique, on constate que le point $C(2\;;\ -2)$ n'est pas sur la droite $(D)$ d'équation $y+2x-1=0.$
Alors, en remplaçant les coordonnées de $C$ dans l'inéquation $y+2x-1>0$, obtient :
$-2+2\times 2-1>0$ si, et seulement si, $1>0.$ Ce qui est toujours vrai.
Donc, les coordonnées du point $C$ vérifient l'inéquation : $y+2x-1>0$
Ce qui signifie que le point $C$ appartient à la solution de cette inéquation représentée par la partie coloriée en rouge.
En observant encore le graphique, nous remarquons que le point $B(0\;;\ 1)$ n'est pas sur la droite $(D')$ d'équation $y+x=0.$
En remplaçant alors ses coordonnées dans l'inéquation $y+x<0$, on a :
$1+0<0$ si, et seulement si, $1<0.$ Ce qui est impossible.
Alors, les coordonnées du point $B$ ne vérifient pas l'inéquation : $y+x<0$
Ce qui signifie que le point $B$ n'appartient pas à la solution de cette inéquation représentée par la partie coloriée en bleu.
Par conséquent, la solution du système $\left\lbrace\begin{array}{rcl} y+2x-1&>&0\\\\y+x&<&0\end{array}\right.$ est la partie coloriée à la fois en bleu et en rouge.
Elle est donc représentée par le secteur angulaire colorié en violet.
Remarque : les demi-droites $[EC)\ $ et $\ [EA)$ n'appartiennent pas à cette solution.

Exercice 14 BFEM 2000
$u\ $ et $\ v$ sont deux applications définies dans $\mathbb{R}$ telles que :
$$u(x)=|x+2|\ \text{ et }\ v(x)=|1-2x|$$
1) Montrons que $u\ $ et $\ v$ sont deux applications affines par intervalle.
On a : $x+2=0$ si, et seulement si, $x=-2$
Donc, $(x+2)$ est positif pour tout $x>-2$ et négatif pour $x<-2.$
En regroupant ces informations dans un tableau de signes, on obtient :
$$\begin{array}{|c|lcccr|}\hline x&-\infty& &-2& &+\infty \\ \hline\text{signe de }(x+2)& &-&|&+& \\ \hline u(x)& &-(x+2)&0&(x+2)& \\ \hline\end{array}$$
Donc,
$-\ $ si $x\in\;\left]-\infty\;;\ -2\right]$ alors, $u(x)=-x-2$
$-\ $ si $x\in\;\left[-2\;;\ +\infty\right[$ alors, $u(x)=x+2$
Ce qui montre que $u$ est une application affine par intervalle.
De la même manière, on a : $1-2x=0$ si, et seulement si, $-2x=-1$
C'est-à-dire ; $x=\dfrac{-1}{-2}=\dfrac{1}{2}$
Dans l'expression $(1-2x)$, on remarque que le coefficient associé à $x$ est négatif.
Donc, $(1-2x)$ est positif pour tout $x<\dfrac{1}{2}$ et négatif pour $x>\dfrac{1}{2}.$
Regroupons ensuite ces informations dans un tableau de signes.
On obtient :
$$\begin{array}{|c|lcccr|}\hline x&-\infty& &1/2& &+\infty \\ \hline\text{signe de }(1-2x)& &+&|&-& \\ \hline v(x)& &(1-2x)&0&-(1-2x)& \\ \hline\end{array}$$
Donc,
$-\ $ si $x\in\;\left]-\infty\;;\ \dfrac{1}{2}\right]$ alors, $v(x)=1-2x$
$-\ $ si $x\in\;\left[\dfrac{1}{2}\;;\ +\infty\right[$ alors, $v(x)=-1+2x$
Par conséquent, $v$ est une application affine par intervalle.
2) Déterminons les valeurs de $x$ pour lesquelles on a : $u(x)=v(x)$
On a : $u(x)=v(x)$ si, et seulement si, $|x+2|=|1-2x|$
Alors,
$\begin{array}{rcl}|x+2|=|1-2x|&\Leftrightarrow&x+2=1-2x\ \text{ ou }\ x+2=-(1-2x)\\\\&\Leftrightarrow&x+2=1-2x\ \text{ ou }\ x+2=-1+2x\\\\&\Leftrightarrow&x+2x=1-2\ \text{ ou }\ x-2x=-1-2\\\\&\Leftrightarrow&3x=-1\ \text{ ou }\ -x=-3\\\\&\Leftrightarrow&x=\dfrac{-1}{3}\ \text{ ou }\ x=3\end{array}$
Ainsi, $|x+2|=|1-2x|$ si, et seulement si, $x=\dfrac{-1}{3}\ $ ou $\ x=3.$
D'où, les valeurs de $x$ pour lesquelles $u(x)=v(x)$ sont :
$$-\dfrac{1}{3}\quad;\quad 3$$
3) Construisons les représentations graphiques de $u\ $ et $\ v$ dans l'intervalle $\left[-2\;;\ \dfrac{1}{2}\right]$
On remarque que :
$$\left[-2\;;\ \dfrac{1}{2}\right]\subset\left[-2\;;\ +\infty\right[$$
Donc, dans l'intervalle $\left[-2\;;\ \dfrac{1}{2}\right]\;,\ u(x)=x+2$
De la même manière, on constate que :
$$\left[-2\;;\ \dfrac{1}{2}\right]\subset\left]-\infty\;;\ \dfrac{1}{2}\right]$$
Donc, dans l'intervalle $\left[-2\;;\ \dfrac{1}{2}\right]\;,\ v(x)=1-2x$
Nous allons alors représenter les droites :
$(\mathcal{D})\ :\ y=x+2\ $ et $\ (\mathcal{D}')\ :\ y=1-2x$ dans l'intervalle $\left[-2\;;\ \dfrac{1}{2}\right].$
Choisissons d'abord deux points $A\;,\ B$ appartenant à $(\mathcal{D})$ et deux points $C\;,\ D$ appartenant à $(\mathcal{D}').$
Soit :
$$\begin{array}{|c|c|c|}\hline&A&B \\ \hline x&-2&0 \\ \hline y&0&2 \\ \hline \end{array}\qquad\qquad \begin{array}{|c|c|c|}\hline&C&D \\ \hline x&\dfrac{1}{2}&0 \\ \hline y&0&1 \\ \hline\end{array}$$
Traçons ensuite la droite $(\mathcal{D})$ passant par $A\;,\ B\ $ et la droite $(\mathcal{D}')$ passant par $C\;,\ D$ tout en restant dans l'intervalle $\left[-2\;;\ \dfrac{1}{2}\right].$

Exercice 15 BFEM 1992
On considère l'expression littérale
$$h(x)=(2x-\sqrt{3})^{2}+2(2x-\sqrt{3})(1+\sqrt{3})+(1+\sqrt{3})^{2}$$
1) Montrons que $h(x)$ est le carré d'une expression littérale
On constate que $h(x)$ est de la forme :
$$a^{2}+2ab+b^{2}=(a+b)^{2}$$
avec $a=(2x-\sqrt{3})\ $ et $\ b=(1+\sqrt{3})$
Donc, en utilisant la forme factorisée des identités remarquables, on obtient :
$\begin{array}{rcl} h(x)&=&(2x-\sqrt{3})^{2}+2(2x-\sqrt{3})(1+\sqrt{3})+(1+\sqrt{3})^{2}\\\\&=&[(2x-\sqrt{3})+(1+\sqrt{3})]^{2}\\\\&=&(2x-\sqrt{3}+1+\sqrt{3})^{2}\\\\&=&(2x+1)^{2}\end{array}$
D'où, $\boxed{h(x)=(2x+1)^{2}}$
2) Résolvons dans $\mathbb{R}$ l'équation $\sqrt{h(x)}-7=0$
On a : $\sqrt{h(x)}-7=0$ si, et seulement si, $\sqrt{(2x+1)^{2}}-7=0$
Or, on sait que : $\sqrt{(2x+1)^{2}}=|2x+1|$
Donc, $\sqrt{(2x+1)^{2}}-7=0$ si, et seulement si, $|2x+1|-7=0$
Alors, en résolvant cette équation, on obtient :
$\begin{array}{rcl} |2x+1|-7=0&\Leftrightarrow&|2x+1|=7\\\\&\Leftrightarrow&2x+1=7\ \text{ ou }\ 2x+1=-7\\\\&\Leftrightarrow&2x=7-1\ \text{ ou }\ 2x=-7-1\\\\&\Leftrightarrow&2x=6\ \text{ ou }\ 2x=-8\\\\&\Leftrightarrow&x=\dfrac{6}{2}\ \text{ ou }\ x=\dfrac{-8}{2}\\\\&\Leftrightarrow&x=3\ \text{ ou }\ x=-4\end{array}$
Ainsi, $|2x+1|-7=0$ si, et seulement si, $x=3\ $ ou $\ x=-4$
Par conséquent, l'équation $\sqrt{h(x)}-7=0$ a pour solution dans $\mathbb{R}\ :$
$$S=\left\lbrace -4\;;\ 3\right\rbrace$$
3) Soit l'expression définie par $k(x)=\sqrt{h(x)}-1$
On a :
$\begin{array}{rcl} k(x)&=&\sqrt{h(x)}-1\\\\&=&\sqrt{(2x+1)^{2}}-1\\\\&=&|2x+1|-1\end{array}$
Donc, $\boxed{k(x)=|2x+1|-1}$
Écrivons alors $k(x)$ sans le symbole de la valeur absolue.
On a : $2x+1=0$ si, et seulement si, $2x=-1$
Ce qui donne : $x=\dfrac{-1}{2}$
Donc, $(2x+1)$ est positif pour tout $x>\dfrac{-1}{2}$ et négatif pour $x<\dfrac{-1}{2}.$
En regroupant ces informations dans un tableau de signes, on obtient :
$$\begin{array}{|c|lcccr|}\hline x&-\infty& &-1/2& &+\infty \\ \hline\text{signe de }(2x+1)& &-&|&+& \\ \hline |2x+1|& &-(2x+1)&0&(2x+1)& \\ \hline\end{array}$$
Donc,
$-\ $ si $x\in\;\left]-\infty\;;\ -\dfrac{1}{2}\right]$ alors, $k(x)=-2x-1-1=-2x-2$
$-\ $ si $x\in\;\left[-\dfrac{1}{2}\;;\ +\infty\right[$ alors, $k(x)=2x+1-1=2x$
a) Déterminons la partie de $\mathbb{R}$ sur laquelle $k$ est une application linéaire.
On a : $k(x)=2x$ est une application linéaire sur $\left[-\dfrac{1}{2}\;;\ +\infty\right[.$
Donc, la partie de $\mathbb{R}$ sur laquelle $k$ est une application linéaire est l'intervalle :
$$\left[-\dfrac{1}{2}\;;\ +\infty\right[$$
b) Déterminons la partie de $\mathbb{R}$ sur laquelle $k$ est une application affine.
On constate que $k(x)=-2x-2$ est une application affine sur $\left]-\infty\;;\ -\dfrac{1}{2}\right].$
Donc, la partie de $\mathbb{R}$ sur laquelle $k$ est une application affine est l'intervalle :
$$\left]-\infty\;;\ -\dfrac{1}{2}\right]$$
c) Représentons graphiquement $k$ dans un repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j})$
Pour cela, nous allons représenter les droites :
$(D)\ :\ y=-2x-2$ dans l'intervalle $\left]-\infty\;;\ -\dfrac{1}{2}\right]$
$(D')\ :\ y=2x$ dans l'intervalle $\left[-\dfrac{1}{2}\;;\ +\infty\right[$
Choisissons deux points $A\;,\ B$ appartenant à $(D)$ et un point $C\in(D').$
Soit :
$$\begin{array}{|c|c|c|}\hline&A&B \\ \hline x&-1&-2 \\ \hline y&0&2 \\ \hline\end{array}\qquad\qquad\begin{array}{|c|c|}\hline&C \\ \hline x&1 \\ \hline y&2 \\ \hline \end{array}$$
Traçons la droite $(D)$ passant par $A\;,\ B$ et la droite $(D')$ passant par $C$ et par l'origine $O$ du repère.

Exercice 16
Soit l'application affine $f$ définie par $f(x)=-5x+3$
1) Calculons l'image par $f$ de chacun des nombres suivants :
$$-3\;;\ \dfrac{1}{2}\;;\ 9\;;\ 0$$
En effet, pour calculer l'image d'un nombre par l'application affine $f$, on remplace $x$ par ce nombre, dans l'expression de $f(x).$
On a alors :
$\begin{array}{rcl} f(-3)&=&-5\times(-3)+3\\\\&=&15+3\\\\&=&18\end{array}$
Ainsi, l'image de $-3$ par $f$ est égale à $18.$
$\begin{array}{rcl} f\left(\dfrac{1}{2}\right)&=&-5\times\left(\dfrac{1}{2}\right)+3\\\\&=&-\dfrac{5}{2}+3\\\\&=&-\dfrac{5}{2}+\dfrac{6}{2}\\\\&=&\dfrac{1}{2}\end{array}$
Donc, $\dfrac{1}{2}$ est l'image de $\dfrac{1}{2}$ par l'application affine $f.$
$\begin{array}{rcl} f(9)&=&-5\times 9+3\\\\&=&-45+3\\\\&=&-42\end{array}$
Ainsi, $-42$ est l'image de $9$ par l'application affine $f.$
$\begin{array}{rcl} f(0)&=&-5\times 0+3\\\\&=&0+3\\\\&=&3\end{array}$
D'où, l'image de $0$ par l'application affine $f$ est égale à $3.$
2) Calculons l'antécédent par $f$ de chacun des nombres suivants :
$$-2\;;\ \dfrac{-4}{3}\;;\ 0\;;\ \sqrt{3}$$
En effet, calculer l'antécédent d'un nombre $b$ revient à trouver un nombre $a$ vérifiant $f(a)=b.$
Pour cela, on doit résoudre l'équation :
$$f(x)=b$$
On a alors :
$\begin{array}{rcl} f(x)=-2&\Leftrightarrow&-5x+3=-2\\\\&\Leftrightarrow&-5x=-2-3\\\\&\Leftrightarrow&-5x=-5\\\\&\Leftrightarrow&x=\dfrac{-5}{-5}\\\\&\Leftrightarrow&x=1\end{array}$
Donc, l'antécédent par $f$ de $-2$ est égal à $1.$
$\begin{array}{rcl} f(x)=\dfrac{-4}{3}&\Leftrightarrow&-5x+3=\dfrac{-4}{3}\\\\&\Leftrightarrow&3\times(-5x+3)=-4\\\\&\Leftrightarrow&-15x+9=-4\\\\&\Leftrightarrow&-15x=-4-9\\\\&\Leftrightarrow&-15x=-13\\\\&\Leftrightarrow&x=\dfrac{-13}{-15}\\\\&\Leftrightarrow&x=\dfrac{13}{15}\end{array}$
Ainsi, $\dfrac{13}{15}$ est l'antécédent de $\dfrac{-4}{3}$ par l'application affine $f.$
$\begin{array}{rcl} f(x)=0&\Leftrightarrow&-5x+3=0\\\\&\Leftrightarrow&-5x=-3\\\\&\Leftrightarrow&x=\dfrac{-3}{-5}\\\\&\Leftrightarrow&x=\dfrac{3}{5}\end{array}$
Donc, l'antécédent par $f$ de $0$ est égal à $\dfrac{3}{5}.$
$\begin{array}{rcl} f(x)=\sqrt{3}&\Leftrightarrow&-5x+3=\sqrt{3}\\\\&\Leftrightarrow&-5x=\sqrt{3}-3\\\\&\Leftrightarrow&x=\dfrac{\sqrt{3}-3}{-5}\\\\&\Leftrightarrow&x=\dfrac{3-\sqrt{3}}{5}\end{array}$
D'où, $\dfrac{3-\sqrt{3}}{5}$ est l'antécédent de $\sqrt{3}$ par l'application affine $f.$
Exercice 17
1) Déterminons l'application affine $f$ de coefficient $-2$ telle que $f(3)=-4$
Comme $f$ est une application affine alors, elle est de la forme :
$$f(x)=ax+b$$
Or, son coefficient est égal à $-2.$
Ce qui signifie que : $a=-2.$
Donc, $f(x)=-2x+b$
Pour déterminer $b$, on calcule $f(3)$ à partir de cette expression de $f(x).$
On a alors : $f(3)=-2\times 3+b=-6+b$
Or, on sait que : $f(3)=-4$
Donc, $-6+b=-4.$
Ce qui donne : $b=-4+6=2$
Par conséquent, $\boxed{f(x)=-2x+2}$
2) Déterminons l'application affine $g$, telle que $g(2)=-1\ $ et $\ g(1)=5.$
Comme $g$ est une application affine alors, $g$ est de la forme :
$$g(x)=ax+b$$
avec, $a$ son coefficient et $b$ son ordonnée à l'origine.
On a : $g(2)=-1\ $ et $\ g(1)=5.$
Donc, le coefficient $a$ est donné par :
$\begin{array}{rcl} a&=&\dfrac{g(2)-g(1)}{2-1}\\\\&=&\dfrac{-1-5}{1}\\\\&=&-6\end{array}$
Alors, $a=-6$
Par suite, $g(x)=-6x+b$
Pour déterminer $b$, on peut calculer $g(1)\ $ ou $\ g(2)$ à partir de l'expression de $g(x).$
On a : $g(2)=-6\times 2+b=-12+b$
Or, $g(2)=-1$ donc, $-12+b=-1$
Ce qui donne : $b=-1+12=11$
D'où, $\boxed{g(x)=-6x+11}$
Exercice 18
On donne les applications affines $f\ $ et $\ g$ définies par :
$$f(x)=2x-5\ \text{ et }\ g(x)=4x$$
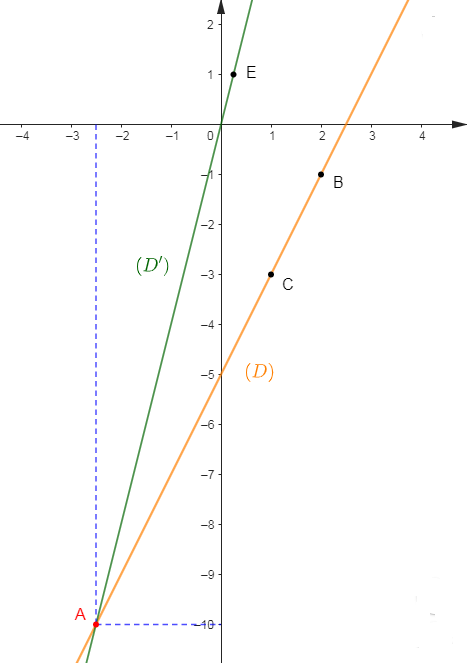
1) Représentons graphiquement ces deux applications dans un même repère orthonormal.
On remarque que $g$ est une application linéaire donc, sa représentation graphique est une droite passant par l'origine du repère.
Pour représenter $f\ $ et $\ g$, on représente donc les droites :
$(D)\ :\ y=2x-5$
$(D')\ :\ y=4x$
Choisissons alors deux points $B\;,\ C$ appartenant à $(D)$ et un point $E\in(D').$
Soit :
$$\begin{array}{|c|c|c|}\hline&B&C \\ \hline x&2&1 \\ \hline y&-1&-3 \\ \hline\end{array}\qquad\qquad\begin{array}{|c|c|}\hline&E \\ \hline x&\dfrac{1}{4} \\ \hline y&1 \\ \hline \end{array}$$
Traçons la droite $(D)$ passant par $B\;,\ C$ et la droite $(D')$ passant par $E$ et par l'origine $O$ du repère.

2) Déterminons graphiquement puis par calcul, les coordonnées de leur point d'intersection $A.$
En effet, à partir du point $A$, en projetant orthogonalement sur les axes du repère, on trouve les coordonnées de $A$ ; point d'intersection des droites $(D)\ $ et $\ (D').$
Ainsi,
l'abscisse de $A$ est égale à : $-\dfrac{5}{2}$
l'ordonnée de $A$ est égale à : $-10$
D'où, $\boxed{A\left(-\dfrac{5}{2}\;;\ -10\right)}$
Pour trouver, par le calcul, les coordonnées de $A$ ; point d'intersection des droites $(D)\ $ et $\ (D')$, nous résolvons le système d'équations formées des équations de $(D)\ $ et $\ (D').$
Soit : $\left\lbrace\begin{array}{rclr} y&=&2x-5&\quad(1)\\\\y&=&4x&\quad(2)\end{array}\right.$
En utilisant la méthode de comparaison, on a :
L'équation $(1)$ est égale à l'équation $(2)$ si, et seulement si, $2x-5=4x$
Alors, en résolvant cette équation, on obtient :
$\begin{array}{rcl} 2x-5=4x&\Leftrightarrow&2x-4x=5\\\\&\Leftrightarrow&-2x=5\\\\&\Leftrightarrow&x=\dfrac{5}{-2}\end{array}$
Donc, $\boxed{x=-\dfrac{5}{2}}$
En remplaçant cette valeur de $x$ dans l'équation $(2)$, on trouve :
$y=4\times\left(-\dfrac{5}{2}\right)=-\dfrac{20}{2}=-10$
Ainsi, $\boxed{y=-10}$
D'où, $\boxed{A\left(-\dfrac{5}{2}\;;\ -10\right)}$
Exercice 19
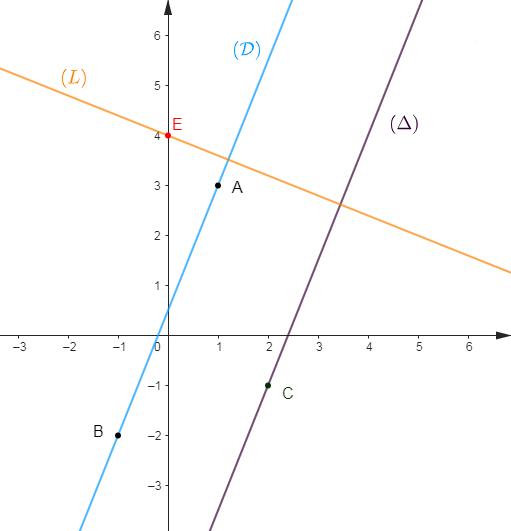
1) Déterminons l'application affine $f$, telle que sa représentation graphique $(\mathcal{D})$ passe par les points $A(1\;;\ 3)\ $ et $\ B(-1\;;\ -2).$
Comme $f$ est une application affine alors, elle est de la forme :
$$f(x)=ax+b$$
avec $a$ son coefficient et $b$ son ordonnée à l'origine.
Comme la représentation graphique de $f$ passe par le point $A(1\;;\ 3)$ alors, cela signifie que l'image de $1$ par $f$ est égale à $3.$
Ce qui s'écrit : $f(1)=3$
Aussi, comme la représentation graphique de $f$ passe par le point $B(-1\;;\ -2)$ alors, cela signifie que l'image de $-1$ par $f$ est égale à $-2.$
Ce qui s'écrit : $f(-1)=-2$
Par suite, le coefficient $a$ est donné par :
$\begin{array}{rcl} a&=&\dfrac{f(1)-f(-1)}{1-(-1)}\\\\&=&\dfrac{3-(-2)}{1+1}\\\\&=&\dfrac{3+2}{2}\\\\&=&\dfrac{5}{2}\end{array}$
Donc, $\boxed{a=\dfrac{5}{2}}$
Ainsi, $f(x)=\dfrac{5}{2}x+b$
Déterminons $b$ en calculant $f(1)$ avec l'expression de $f(x).$
On a : $f(1)=\dfrac{5}{2}\times 1+b=\dfrac{5}{2}+b$
Or, $f(1)=3$
Donc, $\dfrac{5}{2}+b=3$
C'est-à-dire : $b=3-\dfrac{5}{2}=\dfrac{6}{2}-\dfrac{5}{2}$
Ce qui donne : $\boxed{b=\dfrac{1}{2}}$
Par conséquent, l'application affine $f$ est donnée par :
$$f(x)=\dfrac{5}{2}x+\dfrac{1}{2}$$
2) Déterminons l'équation de la droite $(\Delta)$ passant par le point $C(2\;;\ -1)$ et parallèle à $(\mathcal{D}).$
En effet, l'équation de $(\Delta)$ est application affine et est donc de la forme :
$$y=ax+b$$
Comme $(\Delta)$ est parallèle à $(\mathcal{D})$ alors, les deux droites ont même coefficient directeur.
Donc, $a=\dfrac{5}{2}$
Ainsi, $y=\dfrac{5}{2}+b$
Par ailleurs, $(\Delta)$ passe par le point $C(2\;;\ -1).$
Ce qui signifie que les coordonnées de $C$ vérifient l'équation de la droite $(\Delta).$
Donc, en remplaçant les coordonnées de $C$ dans l'équation de $(\Delta)$, on trouve $b.$
On a : $-1=\dfrac{5}{2}\times 2+b$
C'est-à-dire ; $-1=5+b$
Ce qui entraine : $b=-1-5=-6$
D'où, l'équation de la droite $(\Delta)$ est donnée par :
$$y=\dfrac{5}{2}x-6$$
3) Déterminons l'équation de la droite $(L)$ passant par le point $E(0\;;\ 4)$ et perpendiculaire à $(\mathcal{D}).$
En effet, l'équation de la droite $(L)$ est application affine.
Donc, elle est de la forme :
$$y=ax+b$$
Comme les droites $(L)\ $ et $\ (\mathcal{D})$ sont perpendiculaires alors, le produit de leur coefficient directeur est égal à $-1.$
Ce qui signifie : $a\times\dfrac{5}{2}=-1$
Donc, $5a=-2$
Par suite, $a=\dfrac{-2}{5}$
Ainsi, $y=\dfrac{-2}{5}x+b$
Par ailleurs, $(L)$ passe par le point $E(0\;;\ 4).$
Ce qui signifie que les coordonnées de $E$ vérifient l'équation de la droite $(L).$
Donc, en remplaçant les coordonnées de $E$ dans l'équation de $(L)$, on trouve $b.$
On a : $4=\dfrac{-2}{5}\times 0+b$
Ce qui donne : $b=4$
Ainsi, l'équation de la droite $(L)$ est donnée par :
$$y=-\dfrac{2}{5}x+4$$

Exercice 20
On donne l'expression suivante :
$$f(x)=x+1+\sqrt{(2x-3)^{2}}$$
1) Calculons $f(0)\ $ et $\ f(-1).$
En remplaçant $x$ par $0$, dans l'expression de $f(x)$, on a :
$\begin{array}{rcl} f(0)&=&0+1+\sqrt{(2\times 0-3)^{2}}\\\\&=&1+\sqrt{(0-3)^{2}}\\\\&=&1+\sqrt{(-3)^{2}}\\\\&=&1+|-3|\\\\&=&1+3\\\\&=&4\end{array}$
Donc, $\boxed{f(0)=4}$
En remplaçant $x$ par $-1$, dans l'expression de $f(x)$, on obtient :
$\begin{array}{rcl} f(-1)&=&-1+1+\sqrt{(2\times(-1)-3)^{2}}\\\\&=&0+\sqrt{(-2-3)^{2}}\\\\&=&\sqrt{(-5)^{2}}\\\\&=&|-5|\\\\&=&5\end{array}$
Ainsi, $\boxed{f(-1)=5}$
2) Montrons que $f$ est une application affine par intervalles.
En effet, on a : $f(x)=x+1+\sqrt{(2x-3)^{2}}$
Or, on sait que : $\sqrt{(2x-3)^{2}}=\left|2x-3\right|$
Donc, $f(x)=x+1+\left|2x-3\right|$
Écrivons alors $f(x)$ sans le symbole de la valeur absolue.
On a : $2x-3=0$ si, et seulement si, $2x=3$
Ce qui donne : $x=\dfrac{3}{2}$
Donc, $(2x-3)$ est positif pour tout $x>\dfrac{3}{2}$ et négatif pour $x<\dfrac{3}{2}.$
En regroupant ces informations dans un tableau de signes, on obtient :
$$\begin{array}{|c|lcccr|}\hline x&-\infty& &3/2& &+\infty \\ \hline\text{signe de }(2x-3)& &-&|&+& \\ \hline |2x-3|& &-(2x-3)&0&(2x-3)& \\ \hline\end{array}$$
Donc,
$-\ $ si $x\in\;\left]-\infty\;;\ \dfrac{3}{2}\right]$ alors, $|2x-3|=-2x+3$
$-\ $ si $x\in\;\left[\dfrac{3}{2}\;;\ +\infty\right[$ alors, $|2x-3|=2x-3$
Par conséquent :
$f(x)=x+1-2x+3=-x+4$ dans l'intervalle $\left]-\infty\;;\ \dfrac{3}{2}\right]$
$f(x)=x+1+2x-3=3x-2$ dans l'intervalle $\left[\dfrac{3}{2}\;;\ +\infty\right[$
Ce qui montre que $f$ est une application affine par intervalle.
3) Représentons graphiquement l'application $f$ dans un repère orthonormal.
Pour cela, nous allons représenter les droites :
$(D)\ :\ y=-x+4$ dans l'intervalle $\left]-\infty\;;\ \dfrac{3}{2}\right]$
$(D')\ :\ y=3x-2$ dans l'intervalle $\left[\dfrac{3}{2}\;;\ +\infty\right[$
Choisissons deux points $A\;,\ B$ appartenant à $(D)$ et deux points $C\;,\ D$ appartenant à $(D').$
Soit :
$$\begin{array}{|c|c|c|}\hline&A&B \\ \hline x&0&1 \\ \hline y&4&3 \\ \hline\end{array}\qquad\qquad\begin{array}{|c|c|c|}\hline&C&D \\ \hline x&2&3 \\ \hline y&4&7 \\ \hline \end{array}$$
Traçons la droite $(D)$ passant par $A\;,\ B$ et la droite $(D')$ passant par $C\;,\ D.$

4) Résolvons dans $\mathbb{R}$ chacune des équations suivantes : $f(x)=x\;;\ f(x)=x+2.$
Soit : $f(x)=x+1+\left|2x-3\right|$
Alors, on a : $f(x)=x$ si, et seulement si, $x+1+\left|2x-3\right|=x$
C'est-à-dire ; $-x+x+\left|2x-3\right|=-1$
Ce qui donne : $\left|2x-3\right|=-1$
Ce qui est impossible car, la valeur absolue d'un nombre n'est jamais négative.
Donc, il n'existe pas de nombre réel $x$ vérifiant $\left|2x-3\right|=-1.$
Par conséquent, l'équation $f(x)=x$ n'admet pas de solution dans $\mathbb{R}.$
D'où,
$$S=\emptyset$$
On a : $f(x)=x+2$ si, et seulement si, $x+1+\left|2x-3\right|=x+2$
Donc, $-x+x+\left|2x-3\right|=2-1$
Ce qui donne : $f(x)=x+2$ si, et seulement si, $\left|2x-3\right|=1$
Ainsi, en résolvant l'équation $\left|2x-3\right|=1$, on obtient :
$\begin{array}{rcl} \left|2x-3\right|=1&\Leftrightarrow&2x-3=1\ \text{ ou }\ 2x-3=-1\\\\&\Leftrightarrow&2x=1+3\ \text{ ou }\ 2x=-1+3\\\\&\Leftrightarrow&2x=4\ \text{ ou }\ 2x=2\\\\&\Leftrightarrow&x=\dfrac{4}{2}\ \text{ ou }\ x=\dfrac{2}{2}\\\\&\Leftrightarrow&x=2\ \text{ ou }\ x=1\end{array}$
Donc, $x+1+\left|2x-3\right|=x+2$ si, et seulement si, $x=2\ $ ou $\ x=1.$
D'où, l'équation $f(x)=x+2$ a pour solution, dans $\mathbb{R}\ :$
$$S\left\lbrace 1\;;\ 2\right\rbrace$$
II. Un commerçant fixe le prix de vente de chacun de ses articles en prévoyant un bénéfice de $25$ pour cent.
Exercice 21 (BFEM Octobre 2012)
Pour financer une sortie pédagogique, une école décide de vendre les tomates de son jardin.
Le client paye en plus de la quantité de tomates achetée une somme forfaitaire fixe pour le transport.
Un commerçant qui a acheté $300\;kg$ a versé au gestionnaire une somme totale de $125\,000\;F.$
Un membre de l'association des parents d'élèves a acheté $100\;kg$ et a payé $45\,000\;F.$
Calculons le prix d'un kilogramme de tomates et la somme forfaitaire allouée au transport.
Appelons $x$ le prix d'un kilogramme de tomates et $y$ la somme forfaitaire allouée au transport.
Comme le commerçant a acheté $300\;kg$ alors, il doit payer : $300\times x+y$
Or, on sait que ce commerçant à versé au gestionnaire une somme totale de $125\,000\;F.$
Ce qui signifie :
$$300x+y=125\,000\qquad(\text{équation }1)$$
Par ailleurs, un membre de l'association des parents d'élèves a acheté $100\;kg.$
Donc, il doit payer : $100\times x+y$
Comme ce membre de l'association a versé $45\,000\;F$ alors, cela signifie :
$$100x+y=45\,000\qquad(\text{équation }2)$$
Considérons alors le système d'équations suivant, formé des équations $(1)\ $ et $\ (2)\ :$
$$\left\lbrace\begin{array}{rclr} 300x+y&=&125\,000&\quad(1)\\\\100x+y&=&45\,000&\quad(2)\end{array}\right.$$
En multipliant l'équation $(2)$ par $-1$, on obtient :
$$-100x-y=-45\,000\quad(\text{équation }3)$$
$$-100x-y=-45\,000\quad(\text{équation }3)$$
En additionnant membre à membre les équations $(1)\ $ et $\ (3)$, on trouve :
$\begin{array}{rcl} 300x+y-100x-y=125\,000-45\,000&\Rightarrow&200x=80\,000\\\\&\Rightarrow&x=\dfrac{80\,000}{200}\\\\&\Rightarrow&x=400\end{array}$
Donc, $\boxed{x=400}$
Ensuite, en remplaçant cette valeur de $x$ dans l'équation $(1)$, on obtient :
$\begin{array}{rcl} 300\times 400+y=125\,000&\Rightarrow&120\,000+y=125\,000\\\\&\Rightarrow&y=125\,000-120\,000\\\\&\Rightarrow&y=5\,000\end{array}$
Alors, $\boxed{y=5\,000}$
Ainsi, le prix d'un kilogramme de tomates est égal à $400\;F$ et la somme forfaitaire allouée au transport est de $5\,000\;F.$
Exercice 22
Un fournisseur d'accès à Internet propose à ses clients $3$ formules d'abonnement :
$-\ $ Une formule $A$ comportant un abonnement fixe de $12\,000\;F$ par mois auquel s'ajoute le prix des communications au tarif préférentiel de $100\;F$ de l'heure.
$-\ $ Une formule $B$ offrant un libre accès à Internet mais pour laquelle le prix des communications est de $250\;F$ pour une heure de connexion.
$-\ $ Une formule $C$ offrant un libre accès à Internet et comportant une carte d'abonnement annuel de $25\,000\;F.$
Dans les deux premiers cas, les communications sont facturées proportionnellement au temps de connexion.
1) Reproduisons et complétons le tableau suivant :
$$\begin{array}{|c|c|c|c|} \hline &\text{Nombre}&&\\ &\text{d'heures de}&60&80\\ &\text{connexion}& &\\ \hline \text{Prix à payer}&\text{Formule }A&18\,000&20\,000\\ \hline \text{Prix à payer}& \text{Formule }B&15\,000&20\,000\\\hline\text{Prix à payer}&\text{Formule }C&25\,000&25\,000\\ \hline \end{array}$$
2) Pierre se connecte $60$ heures par mois et Fatou $80$ heures par mois.
Déterminons la formule la plus avantageuse pour chacune de ces personnes.
En observant le tableau ci-dessus, nous constatons que, pour $60$ heures de connexion, le prix à payer pour la formule $B$ est moins élevé par rapport au prix des formules $A\ $ et $\ C.$
Par conséquent, la formule $B$ est la plus avantageuse pour Pierre.
D'après le tableau ci-dessus, nous remarquons que, pour $60$ heures de connexion, les prix à payer pour les formules $A\ $ et $\ B$ sont les mêmes et sont moins élevés que le prix associé à la formule $C.$
Donc, la formule $A$ ou la formule $B$ est la plus avantageuse pour Fatou.
3) On note $x$ le temps de connexion d'un client, exprimé en heures.
On appelle $P_{A}$ le prix à payer en $F\;CFA$ avec la formule $A\;,\ P_{B}$ le prix à payer en $F\;CFA$ avec la formule $B\ $ et $\ P_{C}$ le prix à payer en $F\;CFA$ avec la formule $C.$
Exprimons $P_{A}\;,\ P_{B}\ $ et $\ P_{C}$ en fonction de $x.$
On sait que :
pour la formule $A$, on doit payer un abonnement fixe de $12\,000\;F$ par mois et en plus $100\;F$ pour chaque heure de communication.
Donc, pour $x$ heures de communication, le prix $P_{A}$ à payer est donné par :
$$P_{A}=12\,000+100\times x=12\,000+100x$$
la formule $B$ consiste à payer $250\;F$ pour chaque heure de communication.
Ainsi, pour $x$ heures de communication, le prix $P_{B}$ à payer est donné par :
$$P_{B}=250\times x=250x$$
pour la formule $C$, on doit payer uniquement une carte d'abonnement annuel de $25\,000\;F.$
Donc, pour $x$ heures de communication, le prix $P_{C}$ à payer est donné par :
$$P_{C}=25\,000$$
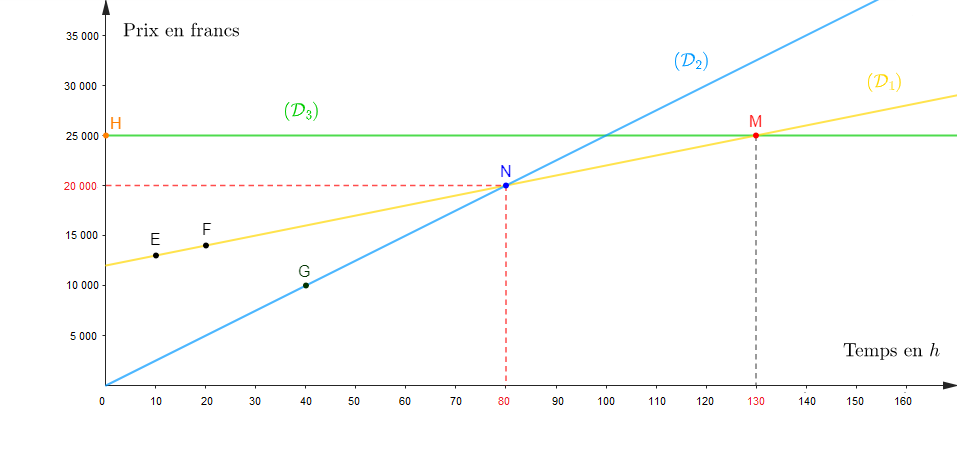
4) Dans un repère orthogonal traçons :
a) la droite $(\mathcal{D}_{1})$, représentation graphique de la fonction
$$f\ :\ x\mapsto 100x+12\,000$$
Soit alors $(\mathcal{D}_{1})$ d'équation : $y=100x+12\,000$
Choisissons deux points $E\ $ et $\ F$ appartenant à $(\mathcal{D}_{1}).$
Soit :
$$\begin{array}{|c|c|c|}\hline&E&F \\ \hline x&10&20 \\ \hline y&13\,000&14\,000 \\ \hline \end{array}$$
$(\mathcal{D}_{1})$ est donc la droite passant par $E\ $ et $\ F$
b) la droite $(\mathcal{D}_{2})$, représentation graphique de la fonction
$$g\ :\ x\mapsto 250x$$
On remarque que $g$ est une application linéaire.
Donc, $(\mathcal{D}_{2})$ d'équation : $y=250x$ est une droite passant par l'origine $O$ du repère.
Choisissons alors un point $G$ et appartenant à $(\mathcal{D}_{2}).$
Soit :
$$\begin{array}{|c|c|}\hline&G \\ \hline x&40 \\ \hline y&10\,000 \\ \hline \end{array}$$
$(\mathcal{D}_{2})$ est donc la droite passant par $G$ et par l'origine du repère.
c) la droite $(\mathcal{D}_{3})$, représentation graphique de la fonction
$$h\ :\ x\mapsto 25\,000$$
Choisissons un point $H$ et appartenant à $(\mathcal{D}_{3}).$
Soit :
$$\begin{array}{|c|c|}\hline&H \\ \hline x&0 \\ \hline y&25\,000 \\ \hline \end{array}$$
$(\mathcal{D}_{3})$ est donc la droite passant par $H$ et parallèle à l'axe des abscisses.

$$\begin{array}{rcl} \text{Echelle }:\ 1\;cm&\longrightarrow&10\;h \\ 1\;cm&\longrightarrow&5\,000\;\text{F}\end{array}$$
Remarque :
$(\mathcal{D}_{1})$ est la représentation graphique du prix à payer pour la formule $A.$
$(\mathcal{D}_{2})$ est la représentation graphique du prix à payer pour la formule $B.$
$(\mathcal{D}_{3})$ est la représentation graphique du prix à payer pour la formule $C.$
5) Moïse, qui a choisi la formule $A$ a payé $20\,000\;F.$
a) Déterminons graphiquement le temps pendant lequel il s'est connecté.
Pour cela, on marque la valeur $20\,000$ sur l'axe des ordonnées puis, à partir de cette valeur on projette sur la droite $(\mathcal{D}_{1})$, parallèlement à l'axe des abscisses.
On obtient alors le point $N$ d'abscisse $80.$
Ce qui signifie que $20\,000\;F$ correspond à $80\;h$ de connexion avec la formule $A.$
Par conséquent, Moïse s'est connecté pendant $80$ heures.
b) Vérifions le résultat par le calcul.
Dans l'expression de $P_{A}$, en remplaçant $P_{A}$ par $20\,000$, on trouve :
$$20\,000=12\,000+100x$$
En résolvant cette équation, on obtient :
$\begin{array}{rcl} 20\,000=12\,000+100x&\Rightarrow&-100x=12\,000-20\,000\\\\&\Rightarrow&-100x=-8\,000\\\\&\Rightarrow&x=\dfrac{-8\,000}{-100}\\\\&\Rightarrow&x=80\end{array}$
Donc, $\boxed{x=80\;h}$
D'où, le temps pendant lequel Moïse s'est connecté est égal à $80$ heures.
6) a) Résolvons dans $\mathbb{R}$ l'inéquation :
$$250x\leq 100x+12\,000$$
On a :
$\begin{array}{rcl} 250x\leq 100x+12\,000&\Leftrightarrow&250x-100x\leq 12\,000\\\\&\Leftrightarrow&150x\leq 12\,000\\\\&\Leftrightarrow&x\leq\dfrac{12\,000}{150}\\\\&\Leftrightarrow&x\leq 80\\\\&\Leftrightarrow&x\in\;]-\infty\;;\ 80]\end{array}$
Comme $x$ représente le temps de connexion alors, $x$ est positif.
Par conséquent, l'inéquation $250x\leq 100x+12\,000$ a pour solution :
$$S=[0\;;\ 80]$$
b) Interprétons le résultat obtenu.
En effet, en observant l'inéquation $250x\leq 100x+12\,000$, on constate que le membre de gauche représente le prix $P_{B}$ et le membre de droite le prix $P_{A}.$
Ainsi, le résultat de la question $2)\,a)$ signifie que le prix $P_{B}$ est inférieur ou égal au prix $P_{A}$ lorsque le temps de connexion est inférieur ou égal à $80$ heures.
Ce qui veut dire que :
pour un temps de connexion inférieur à $80\;h$, la formule $B$ est plus avantageuse que la formule $A$ ;
pour un temps de connexion égal à $80\;h$ les prix à payer sont les même pour les formules $A\ $ et $\ B.$
7) Déterminons graphiquement à partir de quelle durée de connexion par mois la formule $C$ est plus avantageuse que les deux autres.
Sur le graphique, nous constatons que les représentations graphiques des prix $P_{A}\ $ et $\ P_{C}$ se coupent au point $M$ d'abscisse $130.$
Ainsi, lorsque $x\geq 130$, la représentation graphique du prix $P_{C}$ est en dessous de celles des deux autres.
Ce qui signifie qu'à partir de $130$ heures de connexion par mois, la formule $C$ est plus avantageuse que les deux autres.
Exercice de Synthèse
I. On pose $q(x)=|3x-2|.$
1) Montrons que $q$ est une application affine par intervalles.
Étudions alors le signe de $(3x-2).$
On a : $3x-2=0$ si, et seulement si, $3x=2$
Ce qui donne : $x=\dfrac{2}{3}$
Donc, $(3x-2)$ est positif pour tout $x>\dfrac{2}{3}$ et négatif pour $x<\dfrac{2}{3}.$
En regroupant ces informations dans un tableau de signes, on obtient :
$$\begin{array}{|c|lcccr|}\hline x&-\infty& &2/3& &+\infty \\ \hline\text{signe de }(3x-2)& &-&|&+& \\ \hline q(x)& &-(3x-2)&0&(3x-2)& \\ \hline\end{array}$$
Donc,
$-\ $ si $x\in\;\left]-\infty\;;\ \dfrac{2}{3}\right]$ alors, $q(x)=-3x+2$
$-\ $ si $x\in\;\left[\dfrac{2}{3}\;;\ +\infty\right[$ alors, $q(x)=3x-2$
Ce qui montre que $q$ est une application affine par intervalle.
2) Représentons graphiquement $q$ dans un repère orthonormal.
Cela revient donc à représenter les droites :
$(D)\ :\ y=-3x+2$ dans l'intervalle $\left]-\infty\;;\ \dfrac{2}{3}\right]$
$(D')\ :\ y=3x-2$ dans l'intervalle $\left[\dfrac{2}{3}\;;\ +\infty\right[$
Choisissons deux points $A\;,\ B$ appartenant à $(D)$ et deux points $C\;,\ D$ appartenant à $(D').$
Soit :
$$\begin{array}{|c|c|c|}\hline&A&B \\ \hline x&0&-1 \\ \hline y&2&5 \\ \hline\end{array}\qquad\qquad\begin{array}{|c|c|c|}\hline&C&D \\ \hline x&1&2 \\ \hline y&1&4 \\ \hline \end{array}$$
Traçons la droite $(D)$ passant par $A\;,\ B$ et la droite $(D')$ passant par $C\;,\ D.$

II. Un commerçant fixe le prix de vente de chacun de ses articles en prévoyant un bénéfice de $25$ pour cent.
Soit $x$ le prix d'achat d'un article et $p$ son prix de vente.
1) Justifions que :
$$p=\dfrac{5}{4}x$$
En effet, le commerçant prévoit un bénéfice de $25$ pour cent pour chaque article. Cela signifie que ce bénéfice représente $\dfrac{25}{100}$ du prix d'achat de l'article considéré.
Soit $x$ le prix d'achat d'un article et $B$ le bénéfice réalisé sur cet article.
Alors, on a : $B=\dfrac{25}{100}x$
Par suite,
$\begin{array}{rcl} p&=&x+B\\ \\&=&x+\dfrac{25}{100}x\\ \\&=&x+\dfrac{1\times 25}{4\times 25}x\\ \\&=&x+\dfrac{1}{4}x\\ \\&=&\dfrac{4}{4}x+\dfrac{1}{4}x\\ \\&=&\dfrac{5}{4}x\end{array}$
D'où, $\boxed{p=\dfrac{5}{4}x}$
2) Calculons le prix de vente d'un article acheté à $400\text{ F}.$
On a : $p=\dfrac{5}{4}x$ avec, $x=400\text{ F}.$
Donc,
$\begin{array}{rcl} p&=&\dfrac{5}{4}\times 400\\ \\&=&\dfrac{5\times 400}{4}\\ \\&=&500\end{array}$
Ainsi, $\boxed{p=500\text{ F}}$
3) Calculons le prix d'achat d'un article vendu à $1\,250\text{ F}.$
Comme $p=\dfrac{5}{4}x$ alors, $4p=5x$
Ce qui donne : $x=\dfrac{4}{5}p$
Donc, si $p=1250\text{ F}$ alors,
$\begin{array}{rcl} x&=&\dfrac{4}{5}\times 1200\\ \\&=&\dfrac{4\times 1\,200}{5}\\ \\&=&960\end{array}$
D'où, $\boxed{x=960\text{ F}}$
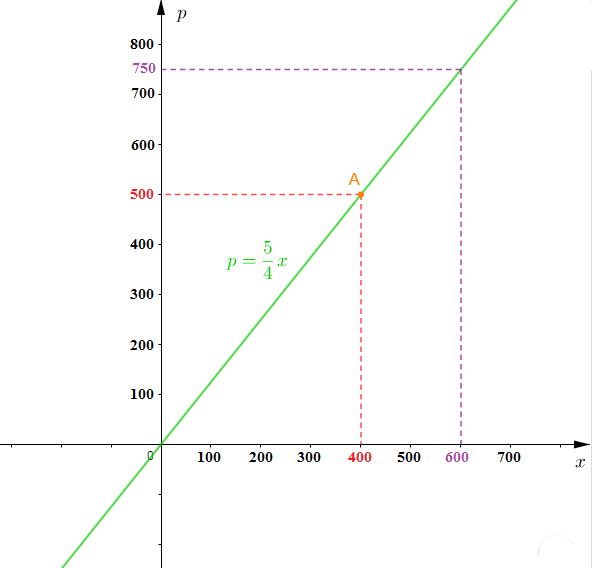
4) Représentons graphiquement dans un repère orthonormal $(O\;,\ \vec{i}\;,\ \vec{j})$, l'application qui à $x$ associe $p.$
Soit $p=\dfrac{5}{4}x$
$p$ est une application linéaire de coefficient linéaire $\dfrac{5}{4}.$
Donc, représenter $p$ revient à tracer droite passant par $O$ origine du repère et par le point $A(400\;;\ 500)$

$$\text{Échelle :}\ 1\;cm\ \longrightarrow\ 100\text{ F}$$
5) Déterminons graphiquement le prix d'achat d'un article vendu à $750\text{ F}.$
Pour se faire, on projette cette valeur de $p$ sur la courbe parallèlement à l'axe des abscisses et à partir de la courbe on procède à une deuxième projection sur l'axe des abscisses parallèlement à l'axe des ordonnées.
Cela correspond alors à $600.$
Par conséquent, le prix d'achat d'un article vendu à $750\text{ F}$ est de $600\text{ F}.$
III. Une fonction affine $f$ définie, pour tout nombre $x$, par
$$f(x)=ax+b$$
On donne : $f(-1)=4\ $ et $\ f(3)=6.$
1) Déterminons $a\ $ et $\ b$
On a : $f(-1)=4\ $ et $\ f(3)=6.$
Donc, le coefficient $a$ de $f$ est donné par :
$\begin{array}{rcl} a&=&\dfrac{f(3)-f(-1)}{3-(-1)}\\\\&=&\dfrac{6-4}{3+1}\\\\&=&\dfrac{2}{4}\\\\&=&\dfrac{1}{2}\end{array}$
Ainsi, $f(x)=\dfrac{1}{2}x+b$
Comme $f(-1)=4$ alors, on a : $\dfrac{1}{2}\times(-1)+b=4$
C'est-à-dire ; $b=4+\dfrac{1}{2}=\dfrac{9}{2}$
D'où, $\boxed{f(x)=\dfrac{1}{2}x+\dfrac{9}{2}}$
2) Soit $g(x)=-2x+9.$
Les représentations graphiques de $f(x)\ $ et $\ g(x)$ sont perpendiculaires.
Justifions.
En effet, les applications $f\ $ et $\ g$ ont pour coefficients respectifs : $\dfrac{1}{2}\ $ et $\ -2.$
Alors, le produit de ces deux coefficient donne :
$$\dfrac{1}{2}\times(-2)=\dfrac{-2}{2}=-1$$
Par conséquent, les représentations graphiques de $f\ $ et $\ g$ sont perpendiculaires.

Auteur:
Diny Faye

Commentaires
Ndeye ba (non vérifié)
mer, 07/15/2020 - 21:01
Permalien
Bonsoir pourais-je avoir les
Rokhaya (non vérifié)
mer, 02/24/2021 - 18:47
Permalien
J'en né besoin pour faire
Anonyme (non vérifié)
dim, 03/06/2022 - 20:35
Permalien
La suite des corrections vous
Anonyme (non vérifié)
jeu, 11/26/2020 - 21:30
Permalien
ttes mes félicitations,
Thierno (non vérifié)
mar, 02/23/2021 - 23:35
Permalien
Correction
Rokhaya (non vérifié)
mer, 02/24/2021 - 18:49
Permalien
Je pourrai avoir le
Rokhaya (non vérifié)
mer, 02/24/2021 - 19:42
Permalien
Je pourrai avoir le
Rokhaya (non vérifié)
jeu, 02/25/2021 - 19:33
Permalien
Oui
Rokhaya (non vérifié)
jeu, 02/25/2021 - 19:33
Permalien
Oui
Rokhaya (non vérifié)
mer, 02/24/2021 - 18:49
Permalien
Je pourrai avoir le
Rokhaya (non vérifié)
mer, 02/24/2021 - 18:49
Permalien
Je pourrai avoir le
Rokhaya (non vérifié)
mer, 02/24/2021 - 18:49
Permalien
Je pourrai avoir le
Sall (non vérifié)
mar, 03/30/2021 - 22:16
Permalien
Pourrai je avoir la
Momar kasse (non vérifié)
lun, 06/21/2021 - 22:46
Permalien
Correction des exo svp
Anonyme (non vérifié)
jeu, 06/24/2021 - 22:11
Permalien
Ce n'est pas svp c'est svt
Anonyme (non vérifié)
jeu, 06/24/2021 - 22:09
Permalien
Correction des autres
Anonyme (non vérifié)
jeu, 06/24/2021 - 22:12
Permalien
Pourrai je avoir la
Anonyme (non vérifié)
dim, 04/24/2022 - 14:28
Permalien
Correction exercice 12
Anonyme (non vérifié)
lun, 04/25/2022 - 00:24
Permalien
Slt je pourrais avoir le
Anonyme (non vérifié)
mer, 05/18/2022 - 23:29
Permalien
Pourrais avoir le corrigé de
Anonyme (non vérifié)
mer, 05/18/2022 - 23:29
Permalien
Svp
Anonyme (non vérifié)
dim, 05/22/2022 - 18:56
Permalien
Bonjour pourrais avoir la
Ajouter un commentaire