Les nombres décimaux arithmétiques 6e
Classe:
Sixième
I. Nombres entiers naturels
I.1 Vocabulaire
Activité 1 :
Parmi les nombres suivants, quels sont les nombres entiers naturels :
$25\;;\ 6\;;\ 4\;;\ \dfrac{4}{7}\;;\ 87\;;\ 468\;;\ 98\;;\ 45\;;\ 5\,964$
Solution
Les nombres : $25\;;\ 6\;;\ 4\;;\ 87\;;\ 468\;;\ 98\;;\ 45\ $ et $\ 5964$ sont des nombres entiers naturels.
Activité 2 :
Parmi les personnes suivantes quelles sont celles qui utilisent les nombres entiers naturels uniquement:
1) Le berger qui compte ses vaches
2) La couturière qui prend les mesures d'un habit en mètre
3) Le menuisier qui mesure les dimensions d'une table en mètre
4) La vendeuse de fruits qui compte ses mangues
Solution
Le berger et la vendeuse de fruits utilisent les nombres entiers naturels uniquement.
Pour compter des objets ou des êtres ; on utilise des nombres entiers naturels.
Exemple :
$73$ livres, $54$ élèves, $3$ écoles, $7$ classes, $4$ salles, $20$ table-bancs, $8$ cahiers
Lorsqu'on compte, on utilise des nombres entier naturels successifs;on dit qu'ils sont consécutifs.
Exemple :
$\{1\;;\ 2\;;\ 3\;;\ 4\;;\ 5\;;\ 6\;;\ 6\;;\ 7\;;\ 8\;;\ 9\;;\ 10\}$
$\{40\;;\ 41\;;\ 42\;;\ 43\;;\ 44\;;\ 45\;; 46\;;\ 47\;;\ 48\;;\ 49\;;\ 50\;;\ 51\;;\ 52\;;\ 53\}$
Activité 3 :
Soit le nombre $1\,253\,445\,930.$
Quels sont les chiffres qui forment ce nombre ?
Représentez l'ensemble $A$ des chiffres de ce nombre.
Solution
Les chiffres qui forment ce nombre sont : $0\;;\ 1\;;\ 2\;;\ 3\;;\ 4\;;\ 5\ $ et $\ 9$
L'ensemble $A$ des chiffres de ce nombre est donné par :
$$A=\{0\;;\ 1\;;\ 2\;;\ 3\;;\ 4\;;\ 5\;;\ 9\}$$
Donc, les chiffres qui forment ce nombre sont les éléments de l'ensemble $A.$
N.B : Dans un ensemble ; un élément est représenté une et une seule fois.
I.2 Notation
L'ensemble des nombres entiers naturels est noté $\mathbb{N}$.
$7$ est un nombre entier naturel donc un élément de $\mathbb{N}.$
On dit que $5$ appartient à $\mathbb{N}$ et on note $$5\in\mathbb{N}$$
Exemples :
$49\in\mathbb{N}\;;\ 45\in\mathbb{N}$
$7$ n'est pas un élément de $A$ ; on dit que $7$ n'appartient pas à $A$ et on note :$$7\notin A$$
$A$ est formé par des nombres entiers naturels appartenant tous à $\mathbb{N}$ ; on dit que $A$ est un sous-ensemble de $\mathbb{N}$ ou $A$ est inclus dans $\mathbb{N}$ et on note $$A\subset\mathbb{N}$$
Donc on a : $A$ est un sous ensemble de $\mathbb{N}$
Soit : $B=\{2\;;\ 8.7\;;\ 13\;;\ 7\;;\ 68.4\;;\ 4778\}$
$B$ renferme des éléments n'appartenant pas à $\mathbb{N}$ donc $B$ n'est pas un sous ensemble de $\mathbb{N}.$
On dit que $B$ n'est pas inclus dans $\mathbb{N}$ et note : $$B\not\subset\mathbb{N}$$
I.3 Écriture en lettres
Exemples :
$7=$ sept
$13=$ treize
$17=$ dix-sept
$47=$ quarante-sept
$87=$ quatre-vingt-sept
$98=$ quatre-vingt-dix-huit
$100=$ cent
$200=$ deux cents
$230=$ deux cent trente
$8\,000=$ huit mille
$3\,785=$ trois mille sept cent quatre-vingt-cinq
$2\,946\,97=$ deux cent quatre-vingt-quatorze mille sept cent quatre-vingt-dix-sept
Remarque :
Mille est invariable ; il ne prend jamais de $"s"$
Vingt et cent prennent $"s"$ lorsqu'ils sont multipliés et placés à la fin de l'écriture d'un nombre.
I.4 Numération de position
$537=500+30+7 $
$5=$ centaines
$3=$ dizaines
$7=$ unités
$28\,695=20\,000+8\,000+600+90+5$
$2=$ dizaines de milliers
$8=$ unités de milliers=milliers
$6=$ centaines
$9=$ dizaines
$5=$ unités
Exemples :
$$45\,078\,893\,536=\underbrace{45}_{MILLIARDS}\quad\underbrace{078}_{MILLIONS}\quad\underbrace{893}_{MILLIERS}\quad\underbrace{536}_{UNITES}$$
II. Nombres décimaux arithmétiques
II.1 Vocabulaire
Activité :
Écrire le nombre suivant sous la forme d'une addition de deux nombres ou deux parties différentes : $147.12$
Solution
On a : $147.12=147+0.12$
Un nombre décimal arithmétique est un nombre qui comprend une partie entière et une partie décimale séparée par une virgule.
Exemples :
$$1.4\left\lbrace\begin{array}{lll} 1 &=& \text{partie entière} \\ 0.4 &=& \text{partie décimale} \end{array}\right.$$
$$147.12\left\lbrace\begin{array}{lll} 147 &=& \text{partie entière} \\ 0.12 &=& \text{partie décimale} \end{array}\right.$$
$$194\left\lbrace\begin{array}{lll} 194 &=& \text{partie entière}\\ 0 &=& \text{partie décimale} \end{array}\right.$$
$$0.901\left\lbrace\begin{array}{lll} 0 &=& \text{partie entière} \\ 0.901 &=& \text{partie décimale} \end{array}\right.$$
$$300.120\left\lbrace\begin{array}{lll} 300 &=& \text{partie entière}\\ 0.120 = 0.12 &=& \text{partie décimale}\end{array}\right.$$
II.2 Notation
L'ensemble des nombres décimaux arithmétiques est noté $\mathcal{D}$ ou $\mathfrak{D}.$
Lorsque la partie décimale d'un nombre arithmétique est nulle ; on obtient un nombre entier naturel. On dit que $\mathbb{N}$ est inclus dans $\mathfrak{D}$ et on note $$\mathbb{N}\subset\mathfrak{D}$$
II.3 Numération de position
$$\,652.17=\underbrace{600}_{CENTAINES}+\underbrace{50}_{DIZAINES}+\underbrace{2}_{UNITES}+\underbrace{0.1}_{DIXIEMES}+\underbrace{0.07}_{CENTIEMES}$$
II.4 Écriture en lettres
$$0.901\left\lbrace\begin{array}{ll}\text{+zéro virgule neuf cent-un}\\ \text{+neuf cent-un millième} \end{array}\right.$$
$$55.75\left\lbrace\begin{array}{ll}\text{+cinquante-cinq virgule soixante-quinze}\\ \text{+cinquante-cinq unités et soixante-quinze centièmes} \end{array}\right.$$
$$1\,648.7\left\lbrace\begin{array}{ll}\text{+mille six cent quarante-huit virgule sept}\\ \text{+mille six cent qurante-huit unité et sept dixièmes} \end{array}\right.$$
II.5 Comparaison
Le signe $"="$ est utilisé pour comparer deux nombres décimaux arithmétiques qui ont la même valeur.
Exemples :
$4.5=4.50\;;\quad 17=17\;;\quad 83.746=83.74600$
Si deux nombres décimaux arithmétiques n'ont pas la même valeur;on utilise le signe $\neq$ pour les comparer.
Exemples :
$739\neq 76\;;\quad 17.17\neq 17.171\;;\quad 21.89\neq 89.21$
Deux nombres différents présentent deux cas d'inégalités:
Une supériorité lorsque le premier est plus grand que le deuxième; on utilise le signe $">"$
Exemples :
$53.23>23.23\;;\quad 728>546\;;\quad 267>134.2638\;;\quad 987.53>456$
Une infériorité lorsque le deuxième est plus petit que le premier;on utilise le signe $"<"$
Exemples :
$7.637<7.639\;;\quad 889<2978.889\;;\quad 10.0009<10.009$
Pour comparer deux nombres décimaux arithmétiques ; on compare leur partie entière en allant de la gauche vers la droite et en comparant les chiffres de même rang.
Si les parties entières sont égales ; on compare les parties décimales en allant de la gauche vers la droites
Exercice d'application :
Comparer les nombres suivants pris deux à deux : $267.01\ $ et $\ 247.01$ ; $241.09\ $ et $\ 241.1$ ; $673.89\ $ et $\ 673.9$ ; $37\ $ et $\ 16$ ; $16\ $ et $\ 37$
Solution
On a :
$267.01>247.01$
$241.09<241.1$
$673.89<673.9$
$37>16$
$16<37$
III. Utilisation des symboles $\cup\ $ et $\ \cap$
Activité :
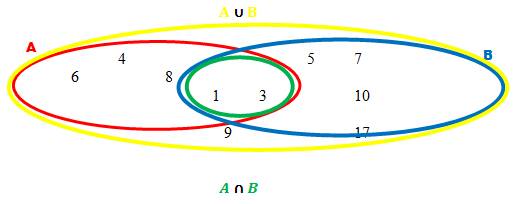
Soient les ensembles: $A=\{ 1\;;\ 3\;;\ 4\;;\ 6\;;\ 8\;;\ 9\}\quad B=\{ 1\;;\ 3\;;\ 5\;;\ 7\;;\ 9\;;\ 10\;;\ 17\}$
Représenter l'ensemble $C$ des éléments appartenant à la fois à $A$ et à $B.$
Représenter l'ensemble $D$ des éléments appartenant à $A$ ou à $B.$
Solution :
$C=\{1\;;\ 3\;;\ 9\}\quad D=\{ 1\;;\ 3\;;\ 4\;;\ 5\;;\ 6\;;\ 7\;;\ 8\;;\ 9\;;\ 10\;;\ 17\}$
L'ensemble $C$ est l'intersection de $A$ et $B$ ; on note : $$A\cap B=C$$
L'ensemble $D$ est l'union de $A$ et $B$ ; on note : $$A\cup B=D$$
IV. Ensembles particuliers
Un ensemble qui est constitué d'un seul élément est un singleton
Exemples
$A=\{1\}\;;\ B=\{0.42\}\;;\ C=\{689\}$
Un ensemble qui n'a pas d'éléments est un ensemble vide ; on le note : $$\emptyset\; \text{ ou }\;\{\emptyset\}$$

Commentaires
Thiam (non vérifié)
ven, 10/19/2018 - 05:51
Permalien
Merci
Anonyme (non vérifié)
jeu, 11/15/2018 - 12:30
Permalien
Cours vraiment clair
LASSANA DIAKHATE (non vérifié)
ven, 01/25/2019 - 01:56
Permalien
bon je trouve les cours tres
Abdou (non vérifié)
ven, 10/18/2019 - 02:40
Permalien
Bon cours
Abdou (non vérifié)
ven, 10/18/2019 - 02:42
Permalien
Bon cours
Alphousseyni SEYDI (non vérifié)
sam, 04/04/2020 - 16:55
Permalien
FELICITATION
Anonyme (non vérifié)
mer, 09/16/2020 - 14:43
Permalien
Merci pour les cours
Sylvestre Fereira (non vérifié)
sam, 11/14/2020 - 13:39
Permalien
Cours très intéressant et
Mame less Ndiaye (non vérifié)
lun, 12/21/2020 - 09:01
Permalien
Contribution
Anonyme (non vérifié)
ven, 08/12/2022 - 12:40
Permalien
pour cours de vacances
Anonyme (non vérifié)
ven, 08/12/2022 - 12:44
Permalien
pour cours de vacances
Marianne (non vérifié)
mar, 09/20/2022 - 12:05
Permalien
Cours trés clair et facile de
Anonyme (non vérifié)
sam, 10/07/2023 - 15:04
Permalien
MERCI
Anonyme (non vérifié)
mer, 10/30/2024 - 21:54
Permalien
j'ai bien compri vos activité
Ajouter un commentaire