Vous êtes ici

Le cosinus d'un angle aigu-4e

Classe:

Quatrième

I. Définition

Étant donné un angle aigu , de mesure

α .

$\alpha.$

Par un point

A

$A$ de

[O x)

$[Ox)$ , on mène la perpendiculaire au côté

[O y)

$[Oy)$ de l'angle.

Cette perpendiculaire coupe

[O y) en H .

$[Oy)\text{ en }H.$

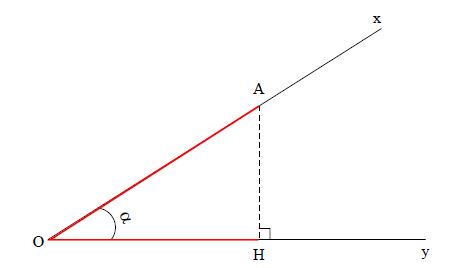
On appelle cosinus de l'angle

\hat{x O y}

$\widehat{xOy}$ , noté

\cos \hat{x O y}

$\cos\widehat{xOy}$ ou

\cos α

$\cos\alpha$ , le quotient

\frac{O H}{O A}

$\dfrac{OH}{OA}$

\cos \hat{x O y} = \frac{O H}{O A}

$\boxed{\cos\widehat{xOy}=\dfrac{OH}{OA}}$

Ce quotient ne dépend pas de la position du point

A

$A$

(même si A est sur le côté [O y) et H sur [O x) .)

$\left(\text{même si }A\text{ est sur le côté }[Oy)\text{ et }H\text{ sur }[Ox).\right)$

Remarque :

\cos α < 1

$\boxed{\cos\alpha<1}$

car

O H < O A

$OH<OA$

(O H)

$\left(OH\right)$ est la plus courte distance de

O

$O$ à

(A H)

$\left(AH\right)$

II. Utilisation de la calculatrice

Lecture d'un cosinus :

La valeur d'un cosinus est indiquée par la fonction

\cos

$\boxed{\cos}$

Exemple :

La calculatrice étant en mode « degré »,

50

$\boxed{50}$

\cos

$\boxed{\cos}$ ou

\cos

$\boxed{\cos}$

50

$\boxed{50}$ indique :

0.64278761 qui est une valeur approchée de ce cosinus.

En général, la valeur utilisée est donnée avec trois chiffres après la virgule, soit, pour cet exemple :

\cos 50^{\circ} \approx 0.643

$\cos 50^{\circ}\approx 0.643$

Recherche d'un angle dont on connaît le cosinus :

La valeur de l'angle est indiquée par la fonction

\cos^{- 1}

$\boxed{\cos^{-1}}$ ou

I N V

$\boxed{INV}$

\cos

$\boxed{\cos}$ ou

2 n d

$\boxed{2\,nd}$

\cos

$\boxed{\cos}$

Exemple :

La calculatrice étant en mode « degré »,

On donne

\cos α = \frac{3}{7}

$\cos\alpha=\dfrac{3}{7}$ les manipulations indiquées ci-dessus (différentes selon le modèle de calculatrice) donnent l'indication : 64.62306647

On obtient donc :

α \approx {64.6}^{\circ}

$\alpha\approx 64.6^{\circ}$

Remarques :

\cos 0^{\circ} = 1

$\cos 0^{\circ}=1$ C'est le cas où :

O H = O A

$OH=OA$

(A et H étant confondus)

$\left(A\text{ et }H\text{ étant confondus}\right)$

\cos 90^{\circ} = 0

$\cos 90^{\circ}=0$ C'est le cas où :

O H = 0

$OH=0$

(H et O étant confondus)

$\left(H\text{ et }O\text{ étant confondus}\right)$

III. Cosinus d'un angle du triangle rectangle

En considérant le triangle rectangle

O A H

$OAH$ vu plus haut, on remarque que

O H

$OH$ est un côté de l'angle droit (celui qui est un coté de l'angle

α

$\alpha$ ) et que

O A

$OA$ est l'hypoténuse.

Le cosinus d'un angle d'un triangle rectangle est le quotient du côté adjacent à cet angle et de l'hypoténuse.

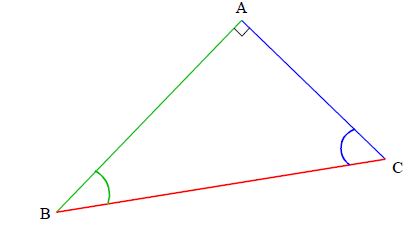
\cos \hat{B} = \frac{A B}{B C}

$\boxed{\cos\widehat{B}=\dfrac{AB}{BC}}$

\cos \hat{C} = \frac{A C}{B C}

$\boxed{\cos\widehat{C}=\dfrac{AC}{BC}}$

IV. Utilité du cosinus

Il complète la propriété de Pythagore en permettant le calcul d'un côté ou d'un angle d'un triangle rectangle.

Recherche d'un côté de l'angle droit

E F G

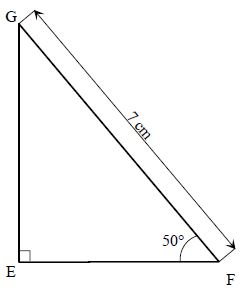
$EFG$ est un triangle rectangle en

E

$E$ ; on sait que :

\hat{F} = 50^{\circ} et F G = 7 c m .

$\widehat{F}=50^{\circ}\text{ et }FG=7\;cm.$

\cos \hat{F} = \frac{E F}{F G}

$\cos\widehat{F}=\dfrac{EF}{FG}$

\cos 50^{\circ} = \frac{E F}{7}

$\cos 50^{\circ}=\dfrac{EF}{7}$

E F = 7 \times \cos 50^{\circ}

$EF=7\times\cos 50^{\circ}$

E F \approx 4.5 c m

$\boxed{EF\approx 4.5\;cm}$

Recherche de l'hypoténuse

M N P

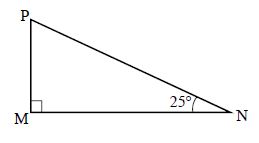
$MNP$ est un triangle rectangle en

M

$M$ ; on sait que :

\hat{N} = 25^{\circ} et M N = 4.5 c m .

$\widehat{N}=25^{\circ}\text{ et }MN=4.5\;cm.$

\cos \hat{N} = \frac{M N}{N P}

$\cos\widehat{N}=\dfrac{MN}{NP}$

\cos 25^{\circ} = \frac{4.5}{N P}

$\cos 25^{\circ}=\dfrac{4.5}{NP}$

N P = \frac{4.5}{\cos 25^{\circ}}

$NP=\dfrac{4.5}{\cos 25^{\circ}}$

N P \approx 5 c m

$\boxed{NP\approx 5\;cm}$

Recherche d'un angle

A B C

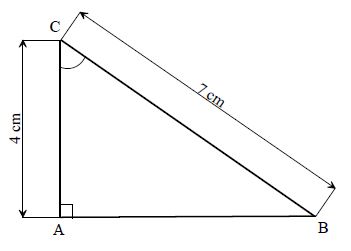
$ABC$ est un triangle rectangle en

A

$A$ ; on sait que :

A C = 3 c m et 7 c m

$AC=3\;cm\text{ et }7\;cm$

\cos \hat{C} = \frac{A C}{B C}

$\cos\widehat{C}=\dfrac{AC}{BC}$

\cos \hat{C} = \frac{4}{7}

$\cos\widehat{C}=\dfrac{4}{7}$

\hat{C} \approx 55^{\circ}

$\widehat{C}\approx 55^{\circ}$

Par conséquent :

\hat{B} = 90^{\circ} - \hat{C} \approx 90^{\circ} - 55^{\circ} = 35^{\circ}

$\widehat{B}=90^{\circ}-\widehat{C}\approx 90^{\circ}-55^{\circ}=35^{\circ}$

$\cos 60^{\circ}$

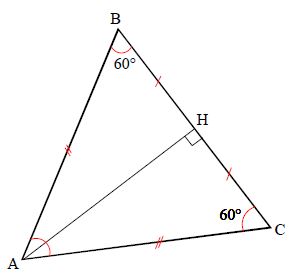
On considère un triangle

A B C

$ABC$ équilatéral dont le côté mesure

a .

$a.$

[A H]

$[AH]$ est une hauteur de ce triangle.

Les angles du triangle

A B C

$ABC$ sont égaux à

60^{\circ}

$60^{\circ}$

On trouve le cosinus de

60^{\circ}

$60^{\circ}$ en calculant, par exemple, le cosinus de l'angle

\hat{B}

$\hat{B}$ du triangle rectangle

A B H .

$ABH.$

\cos \hat{B} = \frac{B H}{A B}

$\cos\widehat{B}=\dfrac{BH}{AB}$

\cos 60^{\circ} = \frac{\frac{a}{2}}{a} = \frac{a}{2} \times \frac{1}{a}

$\cos 60^{\circ}=\dfrac{\dfrac{a}{2}}{a}=\dfrac{a}{2}\times\dfrac{1}{a}$ on simplifie par

a

$a$

\cos 60^{\circ} = \frac{1}{2}

$\boxed{\cos 60^{\circ}=\dfrac{1}{2}}$

Rappel :

égalités équivalentes (utiles pour les calculs de ce chapitre)

a x = b ⟺ x = \frac{b}{a} ⟺ a = \frac{b}{x}

$\boxed{a x=b\Longleftrightarrow x=\dfrac{b}{a}\Longleftrightarrow a=\dfrac{b}{x}}$

comme : 2 \times 3 = 6 ⟺ 3 = \frac{6}{2} ⟺ 2 = \frac{6}{3}

$\text{comme : }\boxed{2\times 3=6\Longleftrightarrow 3=\dfrac{6}{2}\Longleftrightarrow 2=\dfrac{6}{3}}$

Commentaires

Anonyme (non vérifié)

mer, 04/21/2021 - 23:13

Permalien

Hdsc bien merci

répondre

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.

Vous êtes ici

Le cosinus d'un angle aigu-4e

Formulaire de recherche

I. Définition

Remarque :

II. Utilisation de la calculatrice

Lecture d'un cosinus :

Exemple :

Recherche d'un angle dont on connaît le cosinus :

Exemple :

Remarques :

III. Cosinus d'un angle du triangle rectangle

IV. Utilité du cosinus

Recherche d'un côté de l'angle droit

Recherche de l'hypoténuse

Recherche d'un angle

Par conséquent :

Rappel :

Commentaires

Hdsc bien merci

Ajouter un commentaire

Plain text