Série d'exercices : Travail et puissance mécanique - 1er s
Classe:
Première
Exercice 1
Un système constitué de deux blocs reliés par un fil $AB$ de masse négligeable est tiré avec une force constante $F$, d'intensité $300\,N$, sur un plan horizontal rugueux.
On donne $\alpha=60^{\circ}$
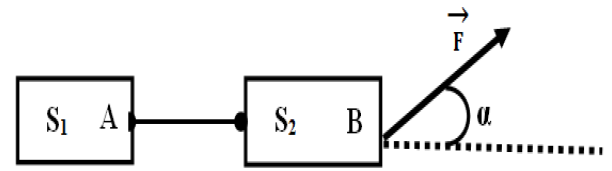
1) Calculer le travail de la force $F$ lorsque le système s'est déplacé de $CD=\,20m.$
2) La vitesse étant constante, la tension du fil horizontal $AB$ qui relie les deux blocs est alors constante et égale à $120\,N.$
Calculer le travail au cours du trajet de la tension du fil appliqué au bloc $S_{2}$ et le travail de la tension du fil appliqué au bloc $S_{1}.$
Calculer le travail total des forces de frottement exercées par le plan sur $S_{1}$ et $S_{2}.$
3) On envisage maintenant le cas où la vitesse n'est plus constante ; la tension du fil varie au cours du mouvement.
Que peut-on dire des travaux de la tension $\overrightarrow{T_{B}}$ appliquée en $B$ et de la tension $\overrightarrow{T_{A}}$ appliquée en $A$ ?
Exercice 2
Alpha tire, à vitesse constante, une luge de masse $m=6.00\,kg$ sur un sol horizontal ; la distance parcourue est $d=AB=100\,m.$
La force $\overrightarrow{F}$ exercée sur la luge par l'intermédiaire de la corde est constante sur la distance $d$ ; la corde fait un angle $\alpha=30.0^{\circ}$ avec le sol.
On suppose que la valeur $f$ des forces de frottements vaut le cinquième du poids $P$ de la luge.
1) Faire l'inventaire des forces qui s'exercent sur le système {luge}.
2) A l'aide d'un schéma, en choisissant un repère judicieux et en projetant sur les axes de ce repère, calculer la valeur de la force de traction qu'exerce Alpha sur sa luge.
3) Calculer le travail de chacune des forces le long du trajet.
Alpha aborde maintenant la piste de luge (de longueur $l=100\,m$) qui forme un plan incliné d'un angle $\beta=15.0^{\circ}$ avec l'horizontale.
Elle tire toujours rectilignement et à vitesse constante ; l'angle entre la corde et la pente est toujours de $30.0^{\circ}.$
On suppose que la force de frottements garde la même valeur $f$ que précédemment.
4) Que peut-on dire du travail de la somme des forces ?
Justifier.
5) Donner l'expression du travail de chacune des forces s'exerçant sur la luge.
6) Comparer les valeurs de la force de traction sur la partie plane et sur la pente.
7) Le déplacement est effectué en $2.0\,min.$
Calculer la puissance moyenne du travail du poids.
Donnée : $g=9.81\,N\cdot kg^{-1}.$
Exercice 3
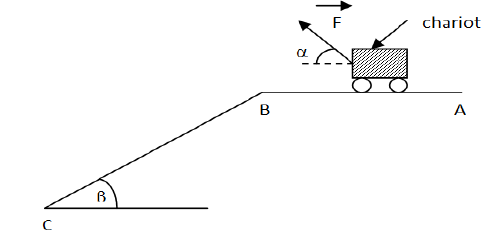
Un chariot de masse $M=20\,Kg$ tiré le long d'une piste horizontale $AB$ de longueur $L=4\,m$ par une force $\overrightarrow{F}$ incliné d'un angle $\alpha=60^{\circ}$ par rapport au déplacement et de valeurs $F=120\,N$ (voir fig).
On néglige tous les frottements.
Le long du trajet $AB$, le chariot est tiré avec une vitesse constante $=1\,m\cdot s^{-1}.$
Exprimer puis calculer :
1) Le travail effectué par $\overrightarrow{F}$ le long du trajet $AB.$
2) La puissance moyenne développée par cette force.
3) En arrivant au point $B$, on supprime la force motrice $\overrightarrow{F}$ et le chariot aborde une piste $BC$ de longueur $L'$ incliné par rapport à l'horizontale passant par $C$ d'un angle $\beta=30^{\circ}.$
Le long du trajet $BC$, le chariot est soumis à des forces de frottement équivalente à une force $\overrightarrow{f}$ constamment opposé au déplacement et de valeur $f=30\,N.$
La différence d'altitude entre les points $B$ et $C$ est $h=2\,m.$
Exprimer puis calculer :
a) le travail du poids $\overrightarrow{P}$ du chariot.
b) Le travail de la force de frottement.
c) Le travail de la réaction $\overrightarrow{R}$ du plan.
Exercice 4
Une barre est maintenue horizontale par l'intermédiaire d'un fil métallique et un fil de coton fixés en son milieu.
Les deux fils sont verticaux, le fil métallique est au-dessus de la barre, le fil de coton en dessous.
Le fil métallique a une constante de torsion $C=4.0\cdot10^{-2}N\cdot m\cdot rad^{-1}.$
Le fil de coton exerce un couple négligeable.
1. Faire un schéma du dispositif.
2. Calculer le travail du couple de torsion dans les situations suivantes :
2.1 On écarte la barre de $90^{\circ}$ par rapport à sa position d'équilibre.
2.2 La barre passe de la position précédente à la position où elle fait un angle de $45^{\circ}$ par rapport à sa position d'équilibre.
2.3 La barre passe de cette dernière position à la position où elle est écartée d'un angle de $30^{\circ}$ de l'autre côté de sa position d'équilibre.
Exercice 5
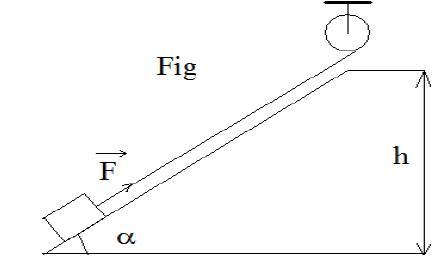
Pour hisser, à vitesse constante, un corps sur une plateforme on utilise un treuil entraîné par un moteur (fig 1).
La masse du corps $M=1000\,kg$, la hauteur $h=2\,m$ et les frottements créent une force $f$ de direction opposée au déplacement.
La force motrice $F=10000\,N$ pour un angle $\alpha=30^{\circ}.$
1) Calculer la force résistante $\left(\overrightarrow{F}\right)$ présentée par le poids : $F'=P\cdot\sin\alpha$ (sens opposé au déplacement) et la force de frottement.
2) Calculer le travail de la force $\overrightarrow{F}$ et la puissance correspondante si la masse se déplace à $0.2\,m/s.$
3) Le treuil ayant un diamètre de $20\,cm$ et un rendement de $0.85.$
Calculer la puissance mécanique du moteur nécessaire, sa vitesse angulaire de rotation, sa fréquence de rotation $(tr/min)$ et le moment du couple moteur.
Exercice 6
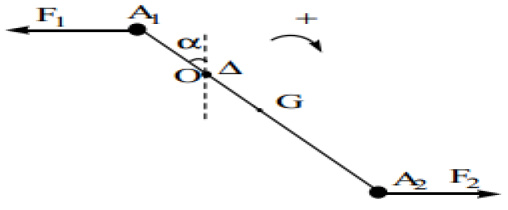
Une tige de cuivre supporte deux boules de fer $($masses identiques $m_{1}=m_{2}=m).$
L'ensemble est mobile sans frottement autour d'un axe horizontal $\Delta$, qui est perpendiculaire en $O$, au plan de la figure.
Le centre d'inertie de la barre $($de masse $M)$ est à la distance $OG=a$ de l'axe.
Un aimant attire la boule de fer en $A_{1}$, avec une force horizontale $F_{1}$ ; un deuxième aimant attire la boule de fer $A_{2}$ avec une force $F_{2}.$
On pose $OA_{1}=\ell_{1}\text{ et }OA_{2}=\ell_{2}$
1) La tige fait un angle α avec la verticale.
a) Représenter les forces extérieures appliquées sur le système (tige$+$boules)
b) Exprimer littéralement les moments de ces forces par rapport à l'axe $\Delta$ en fonction des données.
2) On donne $M=300\,g$, $m=100\,g$ ; $a=6.0\,cm$ ; $\ell_{1}=12\,ccm$ ; $\ell_{2}=24\,cm$ ; $g=9.8\,N/kg.$
Pour la valeur de $=\alpha=20^{\circ}$, l'ensemble est en équilibre.
Déterminer l'intensité commune $F$ des forces $\overrightarrow{F_{1}}$ et $\overrightarrow{F_{2}}$
3) Déterminer le travail effectué par chaque force pendant deux tours
Exercice 7
Un solide ponctuel $S$, de masse $m$, se déplace dans un plan vertical le long d'un trajet $ABCD$ qui comporte deux phases.
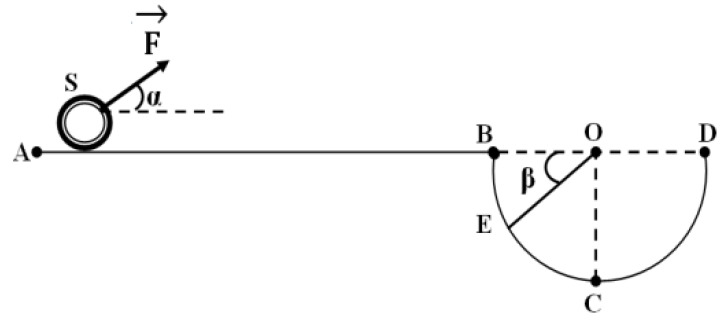
$-\ $ Une partie horizontale $AB$ rectiligne de longueur $8\,m.$
Le long de cette partie, le solide est soumis à une force constante $\overrightarrow{F}$, faisant un angle $\alpha=60^{\circ}$ avec l'horizontale et développant une puissance $P=6\,W$ en plus d'une force de frottement $\overrightarrow{f}$, opposée au déplacement de valeur constante $f=3\,N.$
$-\ $ Une demi sphère $BCD$, de centre $O$ et de rayon $R=0.5\,m$ où le solide est soumis uniquement à son poids $\overrightarrow{P}.$
On donne : $g=10\,N\cdot Kg^{-1}.$
1) Sachant que pendant la partie $AB$ le mouvement est rectiligne uniforme de vitesse $V=2\,m\cdot s^{-1}$,
a) Exprimer la puissance moyenne $P$ développée par $\overrightarrow{F}$ en fonction de $F$, $V$ et $\alpha.$
b) En déduire la valeur de la force $F.$
c) Calculer le travail de la force $\overrightarrow{F}$ pendant le déplacement $AB.$
2) Déterminer le travail de la force de frottement $\overrightarrow{f}$ au cours du déplacement de $AB.$
3) Arrivant au point $B$, on annule les forces $\overrightarrow{F}$ et $\overrightarrow{f}.$
Sachant que le travail du poids de $S$ lorsqu'il glisse de $B$ vers $C$ est $W_{B\rightarrow C}\left(\overrightarrow{P}\right)=0.5\,j$
a) Déterminer la masse du solide $S.$
b) Donner l'expression du travail du poids de $S$ lorsqu'il passe de $B$ vers $E$ en fonction de $m$, $g$, $R$ et $\beta.$
Calculer sa valeur $\left(\beta=30^{\circ}\right)$
c) En déduire le travail du poids de $S$ lors du déplacement de $E$ vers $C.$
4) Déterminer le travail du poids de $S$ lors du déplacement de $C$ vers $D.$
Exercice 8
Un traîneau de masse $m=110\,kg$, tiré par un attelage de chiens, monte une piste enneigée rectiligne de pente $6.0\%$ et de longueur $L=500\,m$ à la vitesse constante $v=25\,km\cdot h^{-1}.$
$($Le centre d'inertie du traîneau s'élève de $6.0\,m$ lorsqu'il parcourt $100\,m.)$
Dans cet exercice le traîneau sera considéré comme un solide en translation.
Les forces de frottement s'opposant au mouvement du traîneau sont équivalentes à une force unique et constante $f$ de valeur $f=70\,N.$
a) Faire le bilan des forces extérieures s'appliquant au traîneau.
Représenter ces forces sur un schéma.
b) Quelle est la résultante de ces forces ?
c) Calculer le travail du poids $\overrightarrow{P}$ et le travail de la force de frottement $\overrightarrow{f}$ pour un déplacement de longueur $L.$
d) En déduire le travail de la force de traction $\overrightarrow{T}$ exercée par les chiens sur le traîneau pour un déplacement de longueur $L.$
Quelle est la puissance moyenne de cette force ?
Exercice 9
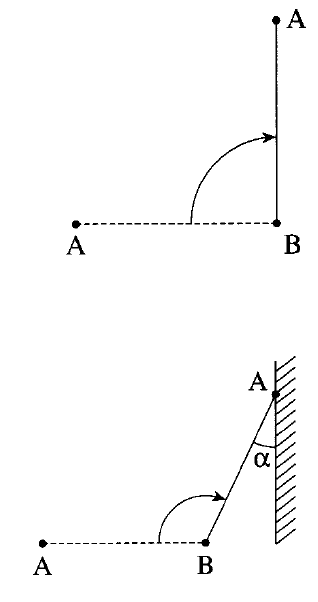
Une échelle $AB$ de longueur $L=3.0\,m$ et de masse $m=10\,kg$ est posée horizontalement sur le sol.
a) L'échelle est soulevée par son extrémité $A$ pour être placée en position verticale, l'extrémité $B$ restant fixe.
Calculer le travail du poids de l'échelle lors de cette opération.
b) L'échelle est soulevée par son extrémité $A$ pour être placée contre un mur, elle fait alors un angle $\alpha=30^{\circ}$ avec le mur.
Calculer le travail du poids de l'échelle lors de cette opération.
Exercice 10
Une voiture descend une côte rectiligne de pente $6.0\%$ et de longueur $L=200\,m$ à la vitesse constante $v=70\,km\cdot h^{-1}.$
Cette voiture tracte une caravane de masse $m=500\,kg.$
$($Le centre d'inertie de la caravane descend de $6.0\,m$ lorsqu'il parcourt $100\,m.)$
Dans cet exercice la caravane sera considérée comme un solide en translation.
Les forces de frottement s'opposant au mouvement de la caravane, dues essentiellement à la résistance de l'air, sont équivalentes à une force unique et constante $\overrightarrow{f}$ de valeur $f=l.0\cdot10^{3}\cdot N.$
a) Faire le bilan des forces extérieures s'appliquant à la caravane.
Représenter ces forces sur un schéma.
b) Quelle est la résultante de ces forces ?
c) Calculer le travail du poids $\overrightarrow{P}$ et le travail de la force de frottement $\overrightarrow{f}$ pour un déplacement de longueur $L.$
d) En déduire le travail de la force de traction $\overrightarrow{T}$ exercée par la voiture sur la caravane pour un déplacement de longueur $L.$
Quelle est la puissance moyenne de cette force ?
e) Quelle devrait être la pente de la côte pour que le travail de $\overrightarrow{T}$ change de signe ?
Quelle serait la signification physique de ce changement de signe ?
Exercice 11 : Le pendule simple
Un pendule est constitué d'une bille de centre $C$ et de masse $m=100\,g$ reliée à un point fixe $O$ par un fil inextensible de longueur $l=50\,cm$ et de masse négligeable.
On écarte le pendule de sa position d'équilibre d'un angle $\theta_{0}=30^{\circ}$ et on le lâche sans vitesse initiale.
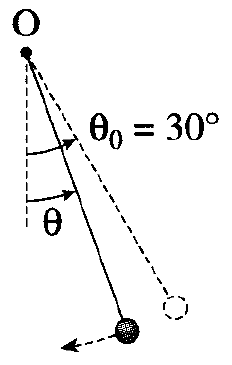
On note $\theta$ l'angle entre le fil et la verticale à un instant quelconque.
a) Calculer le travail du poids de la bille lorsque $\theta$ passe de $\theta_{0}$ à $0.$
b) Calculer le travail du poids de la bille lorsque $\theta_{0}$ passe de $-\theta_{0}.$
c) Peut-on écrire que le travail de la tension du fil entre deux points $A$ et $B$ est $W_{AB}\left(\overrightarrow{T}\right)=\overrightarrow{T}\cdot\overrightarrow{AB}$ ?
Justifier.
d) Quel est le travail de la tension du fil dans les deux cas étudiés précédemment ?
Exercice 12
$S$ est un corps de masse $m=500\,g$ se déplace, à vitesse constante, sur un chemin $ABCDE$ comme l'indique la figure ci-dissous.
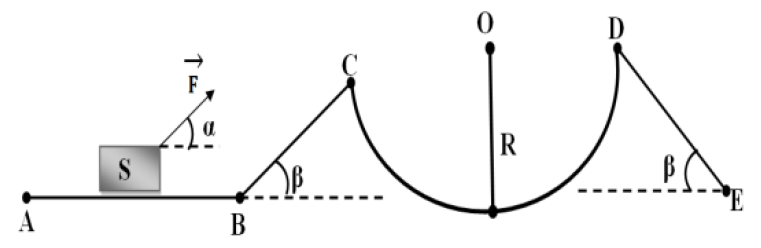
On donne $g=10\,N\cdot Kg^{-1}$ ; $AB=4\,m$ ; $BC=DE=5\,m$, $CD$ est un arc de cercle de rayon $R=2.5\,m$, $\alpha=30^{\circ}$ et $\beta=35^{\circ}$ $F=8\,N$
1) Mouvement $A\ \rightarrow\ B$ :
a) Représenter les forces qui s'exercent sur $S$ sachant que le plan $(AB)$ contient des frottements.
b) Calculer le travail de $\overrightarrow{F}$ et de $\overrightarrow{f}$
c) Quelle est le travail de $\overrightarrow{P}$ ?
Justifier.
2) Mouvement $B\ \rightarrow\ C$ :
a) Calculer $W_{B\rightarrow\,C}\left(\overrightarrow{F}\right)$
b) Calculer $W_{B\rightarrow\,C}\left(\overrightarrow{P}\right)$
3) Calculer $W_{A\rightarrow\,D}\left(\overrightarrow{F}\right)$
4) Dire pourquoi $W_{B\rightarrow\,C}\left(\overrightarrow{F}\right)=W_{D\rightarrow\,E}\left(\overrightarrow{F}\right)$

Commentaires
Pathé (non vérifié)
dim, 01/03/2021 - 22:30
Permalien
Bonjour puisse avoir la
Henri Joël (non vérifié)
sam, 01/09/2021 - 13:05
Permalien
Correction de l'exercice 7
Lamiae (non vérifié)
lun, 11/27/2023 - 13:18
Permalien
Education
Marouane (non vérifié)
dim, 01/21/2024 - 13:22
Permalien
Exercice 7
Anonyme (non vérifié)
ven, 01/15/2021 - 22:33
Permalien
Bien
Albert larry (non vérifié)
dim, 02/28/2021 - 07:50
Permalien
Exercice 2
Mila. Diallo (non vérifié)
sam, 04/10/2021 - 23:18
Permalien
Pc. Svt. Math
Mila. Diallo (non vérifié)
sam, 04/10/2021 - 23:19
Permalien
Pc. Svt. Math
Mila. Diallo (non vérifié)
sam, 04/10/2021 - 23:19
Permalien
Pc. Svt. Math
Mila. Diallo (non vérifié)
sam, 04/10/2021 - 23:19
Permalien
Pc. Svt. Math
emmaboy (non vérifié)
mer, 12/07/2022 - 18:11
Permalien
exercice math pc svt 1 ere D
Mila. Diallo (non vérifié)
sam, 04/10/2021 - 23:19
Permalien
Pc. Svt. Math
Mila. Diallo (non vérifié)
sam, 04/10/2021 - 23:19
Permalien
Pc. Svt. Math
Mila. Diallo (non vérifié)
sam, 04/10/2021 - 23:19
Permalien
Pc. Svt. Math
Mila. Diallo (non vérifié)
sam, 04/10/2021 - 23:19
Permalien
Pc. Svt. Math
Anonyme (non vérifié)
mar, 11/02/2021 - 19:43
Permalien
Merci
Anonyme (non vérifié)
mar, 11/02/2021 - 19:43
Permalien
Merci
Divine (non vérifié)
mar, 11/02/2021 - 19:44
Permalien
Exercices
Divine (non vérifié)
mar, 11/02/2021 - 19:44
Permalien
Exercices
Mamadou Ndiaye (non vérifié)
lun, 11/29/2021 - 18:07
Permalien
Faire des exercices
Mamadou Ndiaye (non vérifié)
lun, 11/29/2021 - 18:08
Permalien
Faire des exercices
Anonyme (non vérifié)
mer, 09/21/2022 - 18:25
Permalien
Etude
Ouattara (non vérifié)
sam, 09/02/2023 - 16:31
Permalien
Ninho
Konaté awa (non vérifié)
dim, 10/08/2023 - 16:32
Permalien
Exercice physique chimie svt et mathématiques
Bachir Abdoulaye (non vérifié)
mar, 03/26/2024 - 00:30
Permalien
Savoir
NUBLAT (non vérifié)
mer, 04/23/2025 - 12:16
Permalien
Physique
Pages
Ajouter un commentaire