Corrigé devoir n° 4 maths - 3e

Classe: 
Troisième
 

Exercice 1

Sur la figure  codée ci-dessous, $ABCD$ est un rectangle tel que : $AB=12\ $ et $\ BC=7.$
 
$E$ est un point du segment $[AD]$ tel que $AE=5.$ La droite $(BE)$ coupe $(DC)$ en $F.$
 
 
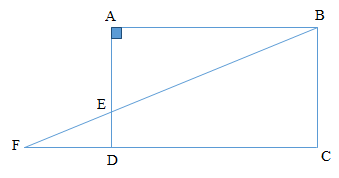
1) Calculons $ED\ $ et $\ EB.$
 
Comme $E\in[AD]$ alors, on a : $AE+ED=AD$
 
Par suite, $ED=AD-AE$
 
Or, $ABCD$ rectangle donc, $AD=BC=7$
 
Ainsi, $ED=7-5=2$
 
D'où, $\boxed{ED=2}$
 
Par ailleurs, le triangle $ABE$ étant rectangle en $A$ alors, d'après le théorème de Pythagore, on a :
EB2=AE2+AB2
Ainsi, 
 
$EB=AE2+AB2=52+122=25+144=169=13$
 
D'où, $\boxed{EB=13}$
 
2) Calculons $EF$  en utilisant la conséquence de THALÈS
 
Les triangles $EFD\ $ et $\ AEB$ étant en position de Thalès alors, en appliquant le théorème de Thalès, on obtient :
EFEB=EDAE
Par suite,
 
$EF=ED×EBAE=2×135=265$
 
D'où, $\boxed{EF=\dfrac{26}{5}=5.2}$
 
3) On prend $EB=13$
 
4) a) Calculons $\sin\widehat{ABE}$
 
On a :
 
$sin⁡ABE^=AEEB=513$
 
Alors, $\boxed{\sin\widehat{ABE}=\dfrac{5}{13}}$
 
b) Calculons  $\cos\widehat{AEB}$
 
On a :
 
$cos⁡AEB^=AEEB=513$
 
Donc, $\boxed{\cos\widehat{AEB}=\dfrac{5}{13}}$

Exercice 2

1) $F=\dfrac{(3-2x)(x-1)}{x-1}$, pour $x=1$ alors, on ne peut pas conclure
 
2) La distance de $3\ $ et $\ \sqrt{2}$ est $|3-\sqrt{2}|$
 
3) $A(-12\;;\ 3)\ $ et $\ B(-5\;;\ 4).$ Les coordonnées du vecteur $\overrightarrow{AB}$ sont $(7\;;\ 1)$
 
4) $\cos 0^{\circ}$ est égal à $1$
 
5) La réunion des intervalles $]-\infty\;;\ 0]\ $ et $\ [2\;;\ 12]$ est $]-\infty\;;\ 0]\cup[2\;;\ 12]$

Exercice 3

On donne :
 
$A=\dfrac{4}{3}-\dfrac{1}{8}\times\left(\dfrac{2}{5}+3\right)\;;\ B=(3-\sqrt{5})^{2}+2(25+\sqrt{45})\ $ et $\ C=\dfrac{-2.4\times 10^{2}\times 5\times 10^{-9}}{3\times 10^{-3}}$
 
1) Calculons $A$ et donnons le résultat sous forme de fraction irréductible
 
$A=43−18×(25+3)=43−18×(25+155)=43−18×175=43−1740=160120−51120=109120$
 
Donc, $\boxed{A=\dfrac{109}{120}}$
 
2) Calculons $B$ et donnons le résultat sous la forme la plus simple possible
 
On a :
 
$B=(3−5)2+2(25+45)=32−2×3×5+(5)2+2×25+2×9×5=9−65+5+50+2×9×5=64−65+2×3×5=64−65+65=64$
 
Ainsi, $\boxed{B=64}$
 
3) Calculons $C$ et donnons son écriture scientifique
 
On a :
 
$C=−2.4×102×5×10−93×10−3=−2.4×5×102×10−9×1033=−12×102−9+33=−4×10−4=−0.0004$
 
Donc, $\boxed{C=-0.0004}$ et sont écriture scientifique est : $\boxed{-4\cdot 10^{-4}}$

Exercice 4

1) On donne l'expression $E=(2x+3)^{2}+(2x+3)(x-6)$
 
a) Développons, ordonnons puis réduisons $E.$
 
On a :
 
$E=(2x+3)2+(2x+3)(x−6)=(2x)2+2×3×(2x)+32+2x2−12x+3x−18=4x2+12x+9+2x2−12x+3x−18=6x2+3x−9$
 
Ainsi, $\boxed{E=6x^{2}+3x-9}$
 
b) Factorisons $E.$
 
Soit : $E=(2x+3)^{2}+(2x+3)(x-6)$ alors, en considérant $(2x+3)$ comme facteur commun, on a :
 
$E=(2x+3)2+(2x+3)(x−6)=(2x+3)[(2x+3)+(x−6)]=(2x+3)(2x+3+x−6)=(2x+3)(3x−3)=3(2x+3)(x−1)$
 
D'où, $\boxed{E=3(x-1)(2x+3)}$
 
2) Calculons $E$ pour $x=0$ puis pour $x=\sqrt{3}.$
 
Soit : $E=6x^{2}+3x-9$ alors
 
$-\ $ en remplaçant $x=0$, on obtient :
 
$E=6×02+3×0−9=0+0−9=−9$
 
Donc, $E=-9$ lorsque $x=0$
 
$-\ $ en remplaçant $x=\sqrt{3}$, on obtient :
 
$E=6×(3)2+3×3−9=6×3+33−9=18+33−9=9+33$
 
Donc, si $x=\sqrt{3}$ alors, $E=9+3\sqrt{3}$
 
3) Trouvons le réel $x$ pour que : $(5x+7)(x-1)=0$
 
On a :
 
$(5x+7)(x−1)=0⇔(5x+7)=0  ou  (x−1)=0⇔5x=−7  ou  x=1⇔x=−75  ou  x=1⇔x∈{−75; 1}$
 
Ainsi, $(5x+7)(x-1)=0$ lorsque $x=-\dfrac{7}{5}$ ou $x=1$
 
4) Soit $F=\dfrac{2x+7}{x+1}$
 
a) Donnons la valeur de $F$ pour $x=\sqrt{2}$
 
En remplaçant $x$ par $\sqrt{2}$, on obtient : $F=\dfrac{2\sqrt{2}+7}{\sqrt{2}+1}$
 
b) Écrivons $F$ sans radical au dénominateur
 
On a :
 
$F=22+72+1=(22+7)(2−1)(2+1)(2−1)=2(2)2−22+72−7(2)2−1=4+52−72−1=−3+521=−3+52$
 
D'où, $\boxed{F=-3+5\sqrt{2}}$
 

Auteur: 
Diny Faye

Commentaires

adama ndiaye (non vérifié)

jeu, 08/11/2022 - 23:44

Veuillez revoir le calcul de EF .

NDEYE Arame (non vérifié)

sam, 02/25/2023 - 20:43

Revoié la calcule de EF car les deux triangles ne sont pas en position de Thalles

fdini

sam, 02/25/2023 - 21:19

pourtant c bien ça

Ajouter un commentaire