Vous êtes ici

Solutions des exercices : Niveaux d'énergie de l'atome - Ts

Classe:

Terminale

Exercice 1

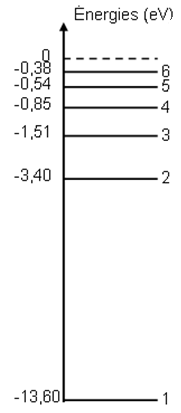
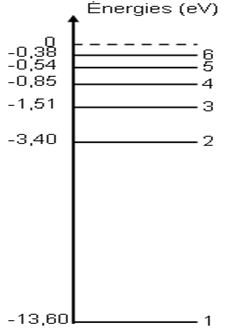
1) Calcul des énergies correspondant à

$n=1\;,\ 2\;,\ 3$ et

$\infty$

$E_{n}=\dfrac{-13.6}{n^{2}}$

$E_{1}=\dfrac{-13.6}{1^{2}}=-13.6\,eV$

$E_{2}=\dfrac{-13.6}{2^{2}}=-3.40\,eV$

$E_{3}=\dfrac{-13.6}{3^{2}}=-1.51\,eV$

$E_{\infty}=\dfrac{-13.6}{\infty}=0\,eV$

Représentation du diagramme des niveaux d'énergie de l'atome d'hydrogène.

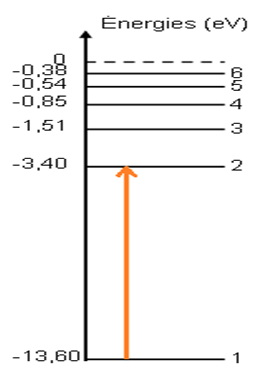
2) L'énergie minimale que l'on doit fournir à un atome d'hydrogène pour qu'il passe de l'état fondamental à un état excité correspond à une transition électronique de l'état fondamental au premier état excité

$($ niveau

$n=2)$

$E=E_{2}-E_{1}=-3.40-(-13.6)$

$\Rightarrow E=10.2eV$

3) Calcul de la longueur d'onde correspondant à cette transition.

$\begin{eqnarray} E &=&\dfrac{hC}{\gamma}\nonumber \\\\\Rightarrow\gamma&=&\dfrac{hC}{E}\nonumber\\\\ &=&\dfrac{6.62\cdot 10^{-34}\times 3.0\cdot 10^{8}}{10.2\times 1.6\cdot 10^{-19}}\nonumber\\\\\Rightarrow\gamma &=&1.22\cdot 10^{-7}m \end{eqnarray}$

4) Calcul de la longueur d'onde de la radiation susceptible d'ioniser l'atome d'hydrogène

$\begin{eqnarray} E_{\infty-E_{1}} &=&\dfrac{hC}{\gamma}\nonumber\\\\\Rightarrow\gamma&=& \dfrac{hC}{E_{\infty}-E_{1}}\nonumber\\\\ &=&\dfrac{6.62\cdot 10^{-34}\times 3.0\cdot 10^{8}}{(0-(-13.6))\times 1.6\cdot 10^{-19}}\nonumber\\\\\Rightarrow\gamma&=&9.13\cdot 10^{-8}m \end{eqnarray}$

Exercice 2

1) a) Montrons que le mouvement de l'électron est uniforme

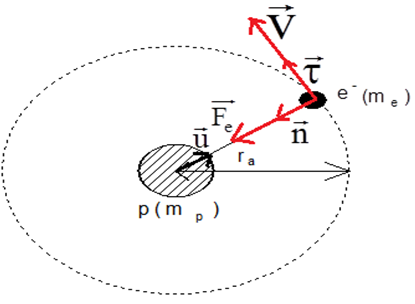
Système étudié : l'électron

Référentiel d'étude : de laboratoire

Bilan des forces appliquées : la force électrostatique

$\overrightarrow{F}$ et le poids négligeable

$\overrightarrow{P}$ devant la force électrostatique

Le théorème du centre d'inertie s'écrit :

$\begin{eqnarray} \overrightarrow{F} &=&m\vec{a}\nonumber\\\\\Rightarrow -\dfrac{ke^{2}}{r^{2}}\overrightarrow{u_{OP}} &=&m\vec{a} \end{eqnarray}$

Projetons cette relation dans le repère de Frenet

$\left(O\;,\ \overrightarrow{u_{t}}\;,\ \overrightarrow{u_{n}}\right)$

$-\$ suivant :

$\overrightarrow{u_{t}}$ :

$\begin{eqnarray} 0 &=&ma_{t}\nonumber\\\\\Rightarrow m\dfrac{\mathrm{d}v}{\mathrm{d}t} &=&0\nonumber\\\\\Rightarrow v &=&\text{constante} \end{eqnarray}$

; le mouvement est donc uniforme

b) Expression de la vitesse

$v$ en fonction de

$k$ ,

$e$ ,

$r$ et

$m$

$-\$ suivant :

$\overrightarrow{u_{n}}$

$\begin{eqnarray} \dfrac{ke^{2}}{r^{2}} &=&ma_{n}\nonumber\\\\\Rightarrow m\dfrac{v^{2}}{r} &=&\dfrac{ke^{2}}{r^{2}} \nonumber\\\\\Rightarrow v &=&\sqrt{\dfrac{ke^{2}}{mr}} \end{eqnarray}$

c) Expression de l'énergie cinétique en fonction de

$k$ ,

$e$ ,

$r$ et

$m$

$\begin{eqnarray} E_{C} &=&\dfrac{1}{2}mv^{2}\nonumber\\\\ &=&\dfrac{1}{2}m\left(\sqrt{\dfrac{ke^{2}}{mr}}\right)^{2} \nonumber\\\\\Rightarrow E_{C} &=&\dfrac{1}{2}\dfrac{ke^{2}}{r} \end{eqnarray}$

d) Exprimer en énergie mécanique

$E$ en fonction de

$k$ ,

$e$ et

$r$

$\begin{eqnarray} E &=& E_{C}+E_{P}\nonumber\\\\ &=&\dfrac{1}{2}\dfrac{ke^{2}}{r}-\dfrac{ke^{2}}{r}\nonumber\\\\ &=&\dfrac{1}{2}\dfrac{ke^{2}}{r}-\dfrac{2ke^{2}}{2r} \nonumber\\\\\Rightarrow E &=&-\dfrac{1}{2}\dfrac{ke^{2}}{r}\nonumber\\\\ E_{r\;\rightarrow\;+\infty} &=&-\dfrac{1}{2}\dfrac{ke^{2}}{r}=0 \end{eqnarray}$

2) a) Détermination de l'expression de

$r_{n}$ en fonction des constantes

$k$ ,

$K$ ,

$m$ ,

$e$ et

$n.$

$\begin{eqnarray} m\dfrac{v^{2}}{r} &=&\dfrac{ke^{2}}{r^{2}}\nonumber\\\\\Rightarrow v^{2}&=&\dfrac{ke^{2}}{mr} \end{eqnarray}$

$\begin{eqnarray} v_{n}r_{n}&=&\dfrac{nK}{m}\nonumber\\\\\Rightarrow\left(v_{n}r_{n}\right)^{2}&=&\left(\dfrac{nK}{m}\right)^{2}\nonumber\\\\\Rightarrow v_{n}^{2}r_{n}^{2}&=&\dfrac{n^{2}K^{2}}{m^{2}}\nonumber\\\\\Rightarrow \dfrac{ke^{2}}{mr_{n}}r_{n}^{2}&=&\dfrac{n^{2}K^{2}}{m^{2}}\nonumber\\\\\Rightarrow r_{n}&=&\dfrac{n^{2}K^{2}m}{ke^{2}m^{2}}\nonumber\\\\\Rightarrow r_{n}&=&\dfrac{K^{2}}{ke^{2}m}n^{2} \end{eqnarray}$

Expression de

$r_{n}$ en fonction de

$r_{1}.$

$\begin{eqnarray} r_{n}&=&\dfrac{K^{2}}{ke^{2}m}n^{2}\nonumber\\\\\Rightarrow r_{1}&=&\dfrac{K^{2}}{ke^{2}m}\nonumber\\\\\Rightarrow r_{n}&=&r_{1}n^{2} \end{eqnarray}$

Calculer

$r_{1}$

$\begin{eqnarray} r_{1}&=&\dfrac{K^{2}}{ke^{2}m}\nonumber\\\\&=&\dfrac{\left(1.054\cdot 10^{-34}\right)^{2}}{9.000\cdot 10^{9}\times\left(1.602\cdot 10^{-19}\right)^{2}\times9.109\cdot 10^{-31}}\nonumber\\\\\Rightarrow r_{1}&=&5.200\cdot 10^{-11}m \end{eqnarray}$

b) Détermination de l'expression de

$E_{n}$ , énergie mécanique de l'électron sur le cercle de rayon

$r_{n}$ , en fonction de

$k$ ,

$K$ ,

$m$ ,

$e$ et

$n$

$\begin{eqnarray} E&=&-\dfrac{1}{2}\dfrac{ke^{2}}{r}\nonumber\\\\\Rightarrow E_{n}&=&-\dfrac{1}{2}\dfrac{ke^{2}}{\dfrac{K^{2}}{ke^{2}m}}n^{2}\nonumber\\\\\Rightarrow E_{n}&=&-\dfrac{k^{2}e^{4}m}{2K^{2}n^{2}} \end{eqnarray}$

Expression de

$E_{n}$ en fonction de

$E_{1}$

$\begin{eqnarray} E_{n}&=&-\dfrac{k^{2}e^{4}m}{2K^{2}n^{2}}\nonumber\\\\\Rightarrow E_{1}&=&-\dfrac{k^{2}e^{4}m}{2K^{2}}\nonumber\\\\\Rightarrow E_{n}&=&-\dfrac{E_{1}}{n^{2}} \end{eqnarray}$

c) Calculer

$E_{1}$ et

$E_{2}$ en électronvolts.

$\begin{eqnarray} E_{1}&=&-\dfrac{k^{2}e^{4}m}{2K^{2}}\nonumber\\\\ E_{1}&=&-\dfrac{\left(9.000\cdot 10^{9}\right)^{2}\left(1.602\cdot 10^{-19}\right)^{4}\times 9.109\cdot 10^{-31}}{2\times\left(1.054\cdot 10^{-34}\right)^{2}}\times\dfrac{1}{1.602\cdot 10^{-19}}\left(1eV=1.602\cdot 10^{-19}J\right)\nonumber\\\\\Rightarrow E_{1}&=&-13.6eV \end{eqnarray}$

$\begin{eqnarray} E_{2}&=&-\dfrac{E_{1}}{2^{2}}\nonumber\\\\ &=&-\dfrac{13.6}{2^{2}}\nonumber\\\\\Rightarrow E_{2}&=&-3.4eV \end{eqnarray}$

L'absorption de l'énergie par l'atome d'hydrogène est la cause du passage de l'énergie de l'électron de

$E_{1}$ à

$E_{2}.$

Exercice 3 L'atome d'hydrogène

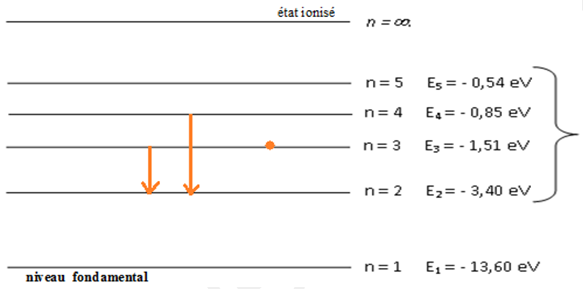
1) Le nom du nombre noté

$"n"$ qui apparaît dans le diagramme est le nombre quantique principal.

2) On dit qu'un atome est dans son état fondamental lorsqu'il se trouve dans le plus bas niveau d'énergie (niveau stable).

L'état fondamental de l'atome d'hydrogène correspond à

$n=1.$

3) Lorsqu'une population d'atomes d'hydrogène est au repos, sans apport d'énergie de la part de l'extérieur, alors ces atomes se trouvent dans l'état fondamental.

4) Le niveau noté :

$n=\infty$ représente l'atome à l'état ionisé.

5) Énergie minimale nécessaire pour ioniser un atome d'hydrogène à partir de son état fondamental

$\Delta E=E_{\infty}-E_{1}=0-(-13.6)\Rightarrow\Delta E=13.6eV$

6) Un atome d'hydrogène qui a la configuration électronique

$n=3$ n'est pas dans son état fondamental, mais dans un état appelé état excité.

7) L'atome d'hydrogène ne peut pas se trouver dans un état situé entre les niveaux

$n=1$ et

$n=2$ , puisque le premier état excité correspond à

$n=2.$

$\bullet\$ On peut exciter cet atome par un photon de lumière dont l'énergie correspond à une transition électronique du niveau

$n=3$ à un niveau supérieur.

$\bullet\$ Montrons qu'en se dés excitant vers le niveau

$2$ , il émet un photon de longueur d'onde :

$\lambda=656.1\,nm.$

$\begin{eqnarray} E_{2}-E_{3}&=&-\dfrac{hC}{\gamma}\nonumber\\\\\Rightarrow\gamma&=&\dfrac{hC}{E_{3}-E_{2}}\nonumber\\\\ &=&\dfrac{6.62\cdot 10^{-34}\times 3.0\cdot 10^{8}}{(-1.51-(-3.40))\times1.6\cdot 10^{-19}}\nonumber\\\\\Rightarrow\gamma&=&6.567\cdot 10^{-7}m\nonumber\\\\\Rightarrow\gamma&=&656.7nm \end{eqnarray}$

Cette radiation est visible, car sa longueur d'onde dans le vide est comprise entre

$400\,nm$ et

$800\,nm.$

9) Détermination de la transition électronique correspondant à l’émission de cette radiation.

$\begin{eqnarray} E_{2}-E_{n}&=&-E\nonumber\\\\\Rightarrow E_{n}&=& E_{2}+E \nonumber\\\\\Rightarrow n^{2} &=&\dfrac{E_{1}}{-E-E_{2}}\nonumber\\\\\Rightarrow n &=& \sqrt{\dfrac{-E_{1}}{E+E_{2}}}\nonumber\\\\\Rightarrow n &=&\sqrt{\dfrac{-13.6}{2.54+(-3.40)}}\nonumber\\\\\Rightarrow n&=&4 \end{eqnarray}$

Calcul de la longueur d'onde correspondante

$\begin{eqnarray} \dfrac{hC}{\gamma} &=&E\nonumber\\\\\Rightarrow\gamma&=&\dfrac{hC}{E}\nonumber\\\\ &=&\dfrac{6.62\cdot 10^{-34}\times 3.0\cdot 10^{8}}{2.54\times 1.6\cdot 10^{-19}}\nonumber\\\\\Rightarrow\gamma&=&4.89\cdot 10^{-7}m\nonumber\\\\\Rightarrow\gamma&=&489 nm \end{eqnarray}$

10) Une lampe à décharge à hydrogène émet un spectre discontinu.

Exercice 4 Niveaux d'énergie de l'atome d'hydrogène

1.1.1 Détermination de l'énergie minimale pour ioniser l'atome d'hydrogène à partir de son état fondamental

$(n=1).$

$\begin{array}{rcl} E&=&E_{\infty}-E_{1}\\\\&=&0-\left(-\dfrac{13.6}{1^{2}}\right)\\\\&=&13.6eV \end{array}$

1.1.2 Détermination de l'énergie minimale pour ioniser l'atome d'hydrogène à partir de son état excité

$n=2$

$\begin{array}{rcl} E&=&E_{\infty}-E_{2}\\\\&=&0-\left(-\dfrac{13.6}{2^{2}}\right)\\\\&=&3.40eV \end{array}$

1.2 Diagramme des niveaux d'énergie de l'atome d'hydrogène :

2.1. Calcul de la différence d'énergie

$\left(E_{3}-E_{1}\right)$ en

$eV$

$\begin{array}{rcl} E_{3}-E_{1}&=&\left(E_{3}-E_{2}\right)+\left(E_{2}-E_{1}\right)\\\\&=&\dfrac{h_{C}}{\lambda_{2}}+\dfrac{h_{C}}{\lambda_{1}}\\\\&=&h_{C}\left(\dfrac{1}{\lambda_{2}}+\dfrac{1}{\lambda_{1}}\right)\\\\\Rightarrow\,E_{3}-E_{1}&=&\dfrac{6.62\cdot 10^{-34}\times 3.0\cdot 10^{8}}{1.6\cdot 10^{-19}}\left(\dfrac{1}{568.8\cdot 10^{-9}}+\dfrac{1}{589\cdot 10^{-9}}\right)\\\\\,E_{3}-E_{1}&=&4.29eV \end{array}$

2.2 Expression de la longueur d'onde

$\lambda$ de ce faisceau en fonction des longueurs d'onde

$\lambda_{1}$ et

$\lambda_{2}$

$\begin{eqnarray} \dfrac{h_{C}}{\lambda} &=&\dfrac{h_{C}}{\lambda_{2}}+\dfrac{h_{C}}{\lambda_{1}}\nonumber\\\\\Rightarrow\dfrac{1}{\lambda} &=&\dfrac{1}{\lambda_{2}}+\dfrac{1}{\lambda_{1}}\nonumber\\\\ &=&\dfrac{\lambda_{2}+\lambda_{1}}{\lambda_{1}\lambda_{2}}\nonumber\\\\\Rightarrow\lambda &=&\dfrac{\lambda_{1}\lambda_{2}}{\lambda_{2}+\lambda_{1}}\nonumber\\\\ &=&\dfrac{589\times 558.8}{568.8+589}\nonumber\\\\\Rightarrow\lambda &=&289.4nm. \end{eqnarray}$

Exercice 5

1) L'énergie

$E_{0}$ correspond à l'énergie d'ionisation de l'atome dans son état fondamental

2) Relation simple existe entre l'énergie de transition

$\Delta E$ d'un niveau

$n$ à un niveau

$p$ du photon émis ou absorbé

$-\$ Lors de l'absorption d'un photon

$n<p$ :

$\begin{array}{rcl} \Delta E &=&\dfrac{h_{C}}{\lambda}\\\\ &=&E_{0}\left(\dfrac{1}{n^{2}}-\dfrac{1}{p^{2}}\right)\\\\\Rightarrow\lambda &=&\dfrac{h_{C}}{E_{0}}\left(\dfrac{1}{n^{2}}-\dfrac{1}{p^{2}}\right) \end{array}$

$-\$ Lors de l'absorption d'un photon

$n<p$ :

$\begin{eqnarray} \Delta E &=& E_{n}-E_{p}\nonumber\\\\ &=&-\dfrac{E_{0}}{n^{2}}-\left(-\dfrac{E_{0}}{p^{2}}\right)\nonumber\\\\ &=& E_{0}\left(\dfrac{1}{p^{2}}-\dfrac{1}{n^{2}}\right) \end{eqnarray}$

et la longueur d'onde du photon émis

$\begin{array}{rcl} E&=&E_{n}-E_{p}\\\\&=&-\dfrac{h_{C}}{\lambda}\\\\&=&\left(-\dfrac{E_{0}}{n^{2}}-\left(-\dfrac{E_{0}}{p^{2}}\right)\right)\\\\&=&E_{0}\left(-\dfrac{1}{n^{2}}+\dfrac{1}{p^{2}}\right)\\\\\Rightarrow\lambda&=&\dfrac{h_{C}}{E_{0}\left(\dfrac{1}{n^{2}}-\dfrac{1}{p^{2}}\right)} \end{array}$

3) a) Montrons que pour une transition d'un niveau

$p$ à un niveau

$n$ tel que

$p>n$ , on peut écrire la relation

$\dfrac{1}{\lambda}=R_{H}\left(\dfrac{1}{n^{2}}-\dfrac{1}{p^{2}}\right).$

Lors d'une transition d'un niveau

$p$ à un niveau

$n$ tel que

$p>n$

$\begin{eqnarray} \Delta E &=&E_{n}-E_{p}\nonumber\\\\ &=&-\dfrac{h_{C}}{\lambda}\nonumber\\\\ &=&\left(-\dfrac{E_{0}}{n^{2}}-\left(-\dfrac{E_{0}}{p^{2}}\right)\right)\nonumber\\\\ &=&E_{0}\left(-\dfrac{1}{n^{2}}+\dfrac{1}{p^{2}}\right)\nonumber\\\\\Rightarrow\dfrac{1}{\lambda} &=&\dfrac{E_{0}}{\lambda}\left(\dfrac{1}{n^{2}}-\dfrac{1}{p^{2}}\right)\nonumber\\\\\Rightarrow\dfrac{1}{\lambda} &=& R_{H}\left(\dfrac{1}{n^{2}}-\dfrac{1}{p^{2}}\right)\nonumber\\\\\text{avec}\quad R_{H} &=&\dfrac{E_{0}}{h_{C}} \end{eqnarray}$

b) Vérifions que

$R_{H}$ (appelée constante de Rydberg) vaut

$R_{H}=1.1\cdot 10^{7}\cdot m^{-1}$

$\begin{array}{rcl} R_{H}&=&\dfrac{E_{0}}{h_{C}}\\\\&=&\dfrac{13.6\times 1.6\cdot 10^{-19}}{6.62\cdot 10^{-34}\times 3.0\cdot 10^{8}}\\\\\Rightarrow\,R_{H}&=&1.1\cdot 10^{7}\cdot m^{-1} \end{array}$

c) Comparons

$\lambda_{3\;,\ 2}$ et

$\lambda_{4\;,\ 2}$

$\lambda_{3\;,\ 2}=\dfrac{h_{C}}{\Delta E_{3\;,\ 2}}$

$\lambda_{4\;,\ 2}=\dfrac{h_{C}}{\Delta E_{4\;,\ 2}}$

$\Delta E_{4\;,\ 2}>\Delta E_{3\;,\ 2}\Rightarrow\lambda_{3\;,\ 2}>\lambda_{4\;,\ 2}$

Calcul des valeurs

$\lambda_{3\;,\ 2}$ et

$\lambda_{4\;,\ 2}$

$\begin{array}{rcl} \dfrac{1}{\lambda}&=&R_{H}\left(\dfrac{1}{n^{2}}-\dfrac{1}{p^{2}}\right)\\\\\Rightarrow\lambda&=&\dfrac{1}{R_{H}\left(\dfrac{1}{n^{2}}-\dfrac{1}{p^{2}}\right)} \end{array}$

$\begin{array}{rcl} \lambda_{3\;,\ 2}&=&\dfrac{1}{R_{H}\left(\dfrac{1}{2^{2}}-\dfrac{1}{3^{2}}\right)}\\\\&=&\dfrac{1}{1.1\cdot 10^{7}\left(\dfrac{1}{2^{2}}-\dfrac{1}{3^{2}}\right)}\\\\\Rightarrow\lambda_{3\;,\ 2}&=&6.55\cdot 10^{-7}m \end{array}$

$\begin{array}{rcl} \lambda_{4\;,\ 2}&=&\dfrac{1}{R_{H}\left(\dfrac{1}{2^{2}}-\dfrac{1}{4^{2}}\right)}\\\\&=&\dfrac{1}{1.1\cdot 10^{7}\left(\dfrac{1}{2^{2}}-\dfrac{1}{4^{2}}\right)}\\\\\Rightarrow\lambda_{4\;,\ 2}&=&4.85\cdot 10^{-7}m \end{array}$

4) Lorsqu'on excite L'atome

$H$ dans son état fondamental à l'aide d'un photon incident d'énergie

$W=13.8eV$ supérieure à l'énergie d'ionisation

$E_{0}=13.6eV$ , l'atome est ionisé et l'électron est éjecté de l'atome avec une énergie cinétique.

Calcul de l'énergie cinétique

$E_{c}$ de l'électron de

$H$ éjecté

$\begin{array}{rcl} E_{c}&=&W-E_{0}\\\\&=&13.8-13.6\\\\\Rightarrow\,E_{c}&=&0.2eV \end{array}$

5) Étudions le comportement l'atome d'hydrogène pris à l'état fondamental

$\left(E_{1}=-13.6eV\right)$ lorsque l'atome entre en choc inélastique avec un électron ayant une énergie cinétique égale

$11eV$

Un gain d'énergie de

$11.0eV$ mènerait l'atome d'hydrogène à une énergie de :

$-13.6+11=-2.6eV$

Cette valeur

$-2.6eV$ ne correspond à aucun niveau d'énergie de l'atome d'hydrogène. Cette absorption d'énergie est impossible.

L'atome

$H$ reste donc au niveau fondamental, l'électron en question n'est pas absorbé.

Exercice 6

1) Couleurs correspondant aux différentes radiations.

Couleur des radiations :

$H_{\alpha}$ : raie rouge

$H_{\beta}$ : radiation bleue

$H_{\lambda}$ : raie indigo

$H_{\delta}$ : raie violette

2.1. La plus petite valeur possible de

$n.$

La longueur d'onde est une grandeur positive ;

$n$ ne peut donc prendre que des valeurs entières positives définies par

$n^{2}-4>0$ donc

$n>2.$

La longueur d'onde minimale de la raie correspondante

Elle correspond à

$n=3$

$\begin{array}{rcl} \lambda &=&\lambda_{0}\dfrac{n^{2}}{n^{2}-4}\\\\&=&367.7\times\dfrac{3^{2}}{3^{2}-4}\\\\\Rightarrow\lambda &=&661.9nm\qquad\text{raie}\ H_{\alpha} \end{array}$

2.2. Valeurs prises

$n$ pour les autres raies visibles du spectre

$\begin{array}{rcl} n=4\Rightarrow\lambda &=&\lambda_{0}\dfrac{n^{2}}{n^{2}-4}\\\\&=&367.7\times\dfrac{4^{2}}{4^{2}-4}\\\\\Rightarrow\lambda &=&490.3nm\qquad\text{raie}\ H_{\beta} \end{array}$

$\begin{array}{rcl} n=5\Rightarrow\lambda &=&\lambda_{0}\dfrac{n^{2}}{n^{2}-4}\\\\&=&367.7\times\dfrac{5^{2}}{5^{2}-4}\\\\\Rightarrow\lambda &=&437.7nm\qquad\text{raie}\ H_{\gamma} \end{array}$

$\begin{array}{rcl} n=6\Rightarrow\lambda &=&\lambda_{0}\dfrac{n^{2}}{n^{2}-4}\\\\&=&367.7\times\dfrac{6^{2}}{6^{2}-4}\\\\\Rightarrow\lambda &=&413.7nm\qquad\text{raie}\ H_{\delta} \end{array}$

3.1. L'énergie de l'atome ne peut prendre que certaines valeurs bien déterminées (discrètes).

Ces valeurs forment une suite discontinue. On dit que l'énergie de l'atome est quantifiée.

$E_{0}$ représente, pour l'atome d'hydrogène, son énergie à l'état fondamental.

3.2. Établissement, en fonction de

$n$ , de la fréquence

$v_{n\;,\ 2}$ des radiations émises lorsque l'atome passe d'un état excité

$n>2$ à l'état excité

$n=2$

$\begin{eqnarray} E_{2}-E_{n} &=&-hv_{n\;,\ 2}\nonumber\\\\\Rightarrow\,v_{n\;,\ 2} &=&\dfrac{E_{n}-E_{2}}{h}\nonumber\\\\&=&\dfrac{E_{0}}{h}\left(-\dfrac{1}{n^{2}}-\left(\dfrac{1}{2^{2}}\right)\right)\nonumber\\\\&=&\dfrac{E_{0}}{h}\left(\dfrac{1}{2^{2}}-\dfrac{1}{n^{2}}\right)\nonumber\\\\&=&\dfrac{E_{0}}{h}\left(\dfrac{1}{4}-\dfrac{1}{n^{2}}\right)\nonumber\\\\\Rightarrow\,v_{n\;,\ 2}&=&\dfrac{E_{0}}{h}\left(\dfrac{n^{2}-4}{4n^{2}}\right)\nonumber\\\\&=&\dfrac{E_{0}}{4h}\left(\dfrac{n^{2}-4}{n^{2}}\right)\nonumber\\\\&=&\dfrac{13.6\times 1.60\cdot 10^{-19}}{4\times 6.62\cdot 10^{-34}}\left(\dfrac{n^{2}-4}{n^{2}}\right)\nonumber\\\\\Rightarrow\,v_{n\;,\ 2}&=&8.22\cdot 10^{14}\left(\dfrac{n^{2}-4}{n^{2}}\right) \end{eqnarray}$

3.3. Retrouvons l'expression empirique de Balmer :

$\lambda=\lambda_{0}\dfrac{n^{2}}{n^{2}-4}.$

$\begin{array}{rcl} v_{n\;,\ 2}&=&\dfrac{c}{\lambda}\\\\\Rightarrow\lambda&=&\dfrac{c}{v_{n\;,\ 2}}\\\\&=&\dfrac{c}{\dfrac{E_{0}}{4h}\left(\dfrac{n^{2}-4}{n^{2}}\right)}\\\\&=&\dfrac{4h_{C}}{E_{0}}\left(\dfrac{n^{2}}{n^{2}-4}\right)\\\\&=&\lambda_{0}\left(\dfrac{n^{2}}{n^{2}-4}\right) \end{array}$

$\begin{array}{rcl} \lambda_{0}&=&\dfrac{4h_{C}}{E_{0}}\\\\&=&\dfrac{4\times 6.62\cdot 10^{-34}\times 3.0\cdot 10^{8}}{13.6\times 1.60\cdot 10^{-19}}\\\\\Rightarrow\lambda_{0}&=&3.65\cdot 10^{-7}m\\\\\Rightarrow\lambda_{0}&=&365nm \end{array}$

$\begin{array}{rcl} \lambda&=&\lambda_{0}\left(\dfrac{n^{2}}{n^{2}-4}\right)\\\\&=&\lambda_{0}\dfrac{1}{1-\dfrac{4}{n^{2}}}\,n\rightarrow\;+\infty\\\\\lambda&=&\lambda_{0}\\\\&=&365nm \end{array}$

Cette radiation de longueur d'onde

$\lambda_{0}$ est émise lorsque l'atome passe de l'état excité

$(n=\infty)$ à l'état excité

$n=2.$

$\lambda_{0}$ est la longueur d'onde limite de la série de Balmer.

Cette radiation est située dans le proche

$UV.$

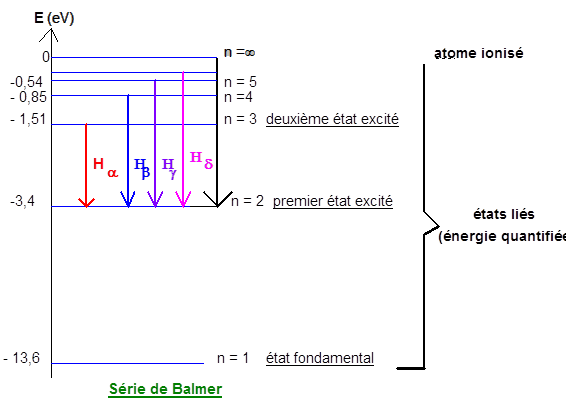
3.4. Tracé du diagramme représentant les transitions entre les différents niveaux d'énergie de l'atome d'hydrogène pour les quatre raies

$H\alpha$ ,

$H\beta$ ,

$H\lambda$ ,

$H\delta$ de la série de Balmer.

4.1. Énergie cinétique minimale d'un électron projectile susceptible de provoquer par choc l'excitation d'un atome d'hydrogène de son état fondamental à son deuxième état excité

$\begin{array}{rcl} E_{c}&=&E_{3}-E_{1}\\\\&=&-1.51-(-13.6)\\\\\Rightarrow\,E_{c}&=&12.1eV \end{array}$

4.2. Il faudra donc accélérer cet électron, initialement immobile, sous une tension de

$12.1V.$

4.3. Détermination des longueurs d'onde des deux photons

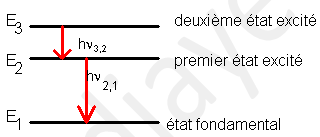
La dés-excitation de l'atome se fait avec l'émission successive de deux photons.

$\ast\$ Un photon, d'énergie

$hv_{3\;,\ 2}$ , est émis lors de la transition du niveau

$E_{3}$ vers le niveau

$E_{2}$ de l'atome.

$E_{3}-E_{2}=hv_{3\;,\ 2}$

La radiation émise correspond à la raie

$H\alpha$ de la série de Balmer

$\lambda=656.5nm.$

$\ast\$ L'autre photon est émis lors de la transition du niveau

$E_{2}$ vers l'état fondamental

$E_{1}$

$\begin{array}{rcl} E_{2}-E_{1}&=&hv_{2\;,\ 1}\\\\&=&h\dfrac{c}{\lambda_{2\;,\ 1}}\\\\\Rightarrow\lambda_{2\;,\ 1}&=&\dfrac{hc}{E_{2}-E_{1}}\\\\\lambda_{2\;,\ 1}&=&\dfrac{6.62\cdot 10^{-34}\times 3\cdot 10^{8}}{10.2\times 1.6\cdot 10^{-19}}\\\\&=&1.22\cdot 10^{-7}m\\\\&=&122nm \end{array}$

Ce rayonnement est situé dans l'ultraviolet

Exercice 7 : Étoile Vega et son spectre

1) Le spectre est un spectre discontinu car ce spectre est constitué de raies.

2) L'étoile possède une atmosphère puisque son spectre est inclus à celui du visible.

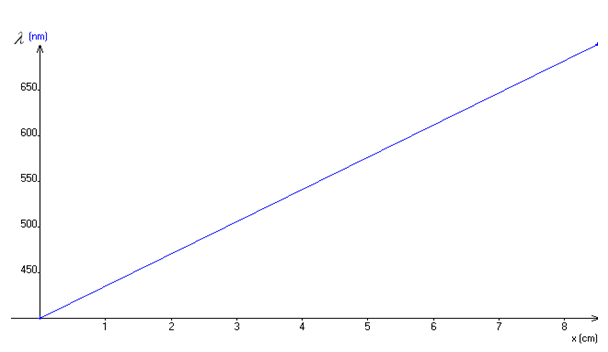
3) Tracé de

$\lambda$ en fonction de

$x.$

4) Coefficient directeur et ordonnée à l'origine de la droite.

$\begin{array}{rcl} a&=&\dfrac{\Delta\lambda}{\Delta x}\\\\&=&\dfrac{700-400}{8.5-0}\\\\\Rightarrow\,a&=&35.3nm\cdot cm^{-1} \end{array}$

$\begin{array}{rcl} \lambda&=&ax+b\\\\\Rightarrow\,x&=&0\\\\\Rightarrow\lambda&=&b\\\\&=&400nm \end{array}$

Équation numérique de

$\lambda=ax+b$

$\lambda=35.3x+400$

5) Valeurs des longueurs d'onde émises par l'étoile

$\begin{array}{rcl} \lambda&=&35.3x+400\\\\\Rightarrow\,x&=&0\\\\\Rightarrow\lambda&=&400nm \end{array}$

$\begin{array}{rcl} x&=&8.5\\\\\Rightarrow\lambda&=&35.3\times 8.5+400\\\\\Rightarrow\lambda&=&700nm \end{array}$

6) La majeur partie des longueurs d'onde émise par l'hydrogène ou par l'hélium appartiennent au spectre de l'étoile Véga. L'étoile Véga contient de l'hydrogène et de l'hélium, donc de l'atmosphère.

Exercice 8

1) Justification de la discontinuité du spectre d'émission.

Les spectres d'émission de l'atome d'hydrogène observés sont des raies.

a) L'état fondamental de l'atome correspond à l'état stable de l'atome

b) L'énergie d'ionisation de l'atome d'hydrogène est l'énergie minimale qu'il fournir à l'atome d'hydrogène, situé dans son état fondamental, pour lui arracher son électron

$\begin{array}{rcl} E&=&E_{\infty}-E_{1}\\\\&=&0-(-13.6) \end{array}$

2) a) Calcul de la longueur d'onde maximale

$\lambda_{\text{max}}$ correspondant à la transition de l'électron d'un niveau

$n>2$ au niveau

$2.$

Cette longueur d'onde correspond à une transition électronique du niveau

$n=3$ au niveau

$n=2$

$\begin{array}{rcl} -\dfrac{h_{C}}{\lambda_{\text{max}}}&=&E_{2}-E_{3}\\\\\Rightarrow\lambda&=&\dfrac{h_{C}}{E_{3}-E_{2}}\\\\&=&\dfrac{6.62\cdot 10^{-34}\times 3\cdot 10^{8}}{1.602\cdot 10^{-19}\times(-1.51-(-3.40))}\\\\\Rightarrow\lambda_{\text{max}}&=&657nm \end{array}$

$\lambda_{\text{max}}\approx\lambda_{4}$

b) Transitions correspondant aux radiations de longueur d'onde

$\lambda_{1}$ ,

$\lambda_{2}$ et

$\lambda_{3}.$

Les longueurs d'onde appartiennent au spectre visible correspondant à la transition de l'électron d'un niveau

$n>2$ au

$n.$

$\begin{array}{rcl} \bullet\text{ pour }\lambda&=&\lambda_{1}\\\\\Rightarrow\,E_{n}&=&E_{2}+\dfrac{h_{C}}{\lambda_{1}}\\\\&=&-3.40+\dfrac{6.62\cdot 10^{-34}\times 3\cdot 10^{8}}{410\cdot 10^{-9}\times 1.6\cdot 10^{-19}}\\\\\Rightarrow\,E_{n}&=&-0.37eV \end{array}$

La transition correspond au niveau

$n=6$ au niveau

$n=2$

$\begin{array}{rcl} \bullet\text{ pour }\lambda&=&\lambda_{2}\\\\\Rightarrow\,E_{n}&=&E_{2}+\dfrac{h_{C}}{\lambda_{2}}\\\\&=&-3.40+\dfrac{6.62\cdot 10^{-34}\times 3\cdot 10^{8}}{434.1\cdot 10^{-9}\times 1.6\cdot 10^{-19}}\\\\\Rightarrow\,E_{n}&=&-0.5eV \end{array}$

La transition correspond au niveau

$n=5$ au niveau

$n=2$

$\begin{array}{rcl} \bullet\text{ pour }\lambda&=&\lambda_{3}\\\\\Rightarrow\,E_{n}&=&E_{2}+\dfrac{h_{C}}{\lambda_{3}}\\\\&=&-3.40+\dfrac{6.62\cdot 10^{-34}\times 3\cdot 10^{8}}{486.1\cdot 10^{-9}\times 1.6\cdot 10^{-19}}\\\\\Rightarrow\,E_{n}&=&-0.85eV \end{array}$

La transition correspond au niveau

$n=4$ au niveau

$n=2.$

3) a) Ce photon est absorbé car l'énergie correspondant à la longueur d'onde est égale à la différence d'énergie entre le niveau

$n=2$ et le niveau

$n=4$

b) L'atome est ionisé si l'énergie absorbée

$E$ est supérieure ou égale à l'énergie d'ionisation

$E_{0}.$

$E=11eV<E_{0}=13.6eV$ ; l'énergie du photon est inférieure à l'énergie d'ionisation, l'atome ne sera pas ionisé

$E=11eV<E_{0}=13.6eV$ ; l'énergie cinétique de l'électron est inférieure à l'énergie d'ionisation, l'atome ne sera pas ionisé

$E=14.3eV>E_{0}=13.6eV$ ; l'énergie du photon est supérieure à l'énergie d'ionisation, l'atome sera ionisé et l'électron qui l'atome avec l'énergie restante sous d'énergie cinétique.

$\begin{array}{rcl} E_{C}&=&E-E_{0}\\\\&=&14.3-13.6\\\\\Rightarrow\,E_{C}&=&0.7eV \end{array}$

Auteur:

Amary Thiam & Sidy Mouhamed Ndiaye

Commentaires

Ama dickel Ba (non vérifié)

dim, 03/02/2025 - 22:55

Permalien

Vous avez sautée la

Vous avez sautée la correction de l'exercice 4 concernant la figure représente un diagramme très simplifié des niveaux d'énergie de l'atome de lithium

répondre

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.

Vous êtes ici

Solutions des exercices : Niveaux d'énergie de l'atome - Ts

Formulaire de recherche

Exercice 1

Exercice 2

Exercice 3 L'atome d'hydrogène

Exercice 4 Niveaux d'énergie de l'atome d'hydrogène

Exercice 5

Exercice 6

Exercice 7 : Étoile Vega et son spectre

Exercice 8

Commentaires

Vous avez sautée la

Ajouter un commentaire

Plain text