Solution des exercices : Poids d'un corps - relation poids masse - 4e
Classe:
Quatrième
Exercice 1
Complétons ces phrases à trous par les mots ou groupes de mots suivants :
intensité ; $g$ ; vertical ; point d'application ; dynamomètre ; altitude; poids ; rectiligne ; proportionnelles ; latitude ; des caractéristiques ; newton ; vectorielle ; $P=mg$ ; le sens ; direction ; vecteur.
Dans son voisinage, la terre attire chaque objet ; cette attraction est appelée poids de l'objet.
Dans un même lieu, deux objets distincts peuvent être attirés différemment par la terre.
On dit que le poids d'un objet possède une intensité.
L'intensité du poids s'exprime en newton et se mesure à l'aide d'un dynamomètre.
Les objets sont toujours attirés vers le bas par la terre : ceci correspond au sens du poids.
Pendant une chute, une mangue attirée par la terre suit un trajet rectiligne et vertical ; le poids possède alors une direction.
L'intensité, le sens et la direction sont des caractéristiques ; l'autre caractéristique est le point d'application.
A cause de ces quatre caractéristiques, le poids est une grandeur vectorielle ; il est représenté par un vecteur.
L'intensité du poids et la masse sont proportionnelles et sont reliées par la relation $P=mg.$
L'intensité de la pesanteur notée $g$ ; elle varie en latitude et en altitude.
Exercice 2
Mettons une croix dans la case qui correspond à la bonne réponse :
Le poids d'un objet est :
$\boxed{\times}\ $ l'attraction terrestre
$\boxed{\ }\ $ l'attraction lunaire
$\boxed{\ }\ $ l'attraction d'un aimant
Le déplacement d'un objet du haut vers le bas correspond :
$\boxed{\ }\ $ à la direction du poids
$\boxed{\ }\ $ à l'intensité du poids
$\boxed{\times}\ $ au sens du poids
L'intensité du poids s'exprime en :
$\boxed{\ }\ $ kilogramme
$\boxed{\times}\ $ newton
$\boxed{\ }\ $ mètre
L'intensité du poids se mesure avec :
$\boxed{\ }\ $ une balance
$\boxed{\ }\ $ un rapporteur
$\boxed{\times}\ $ un dynamomètre
L'intensité du poids et la masse d'un objet sont :
$\boxed{\ }\ $ égales
$\boxed{\ }\ $ opposées
$\boxed{\times}\ $ proportionnelles
La relation entre l'intensité du poids $P$ et la masse $m$ d'un objet est :
$\boxed{\ }\ \ P=\dfrac{m}{g}$
$\boxed{\times}\ \ P=m.g$
$\boxed{\ }\ \ P=\dfrac{g}{m}$
L'intensité de la pesanteur a pour unité :
$\boxed{\times}\ \ N.kg^{-1}$
$\boxed{\ }\ \ N.kg$
$\boxed{\ }\ \ N^{-1}.kg$
Exercice 3
L'intensité du poids d'un objet est $P=750\;N.$
1) Donnons les caractéristiques de ce poids.
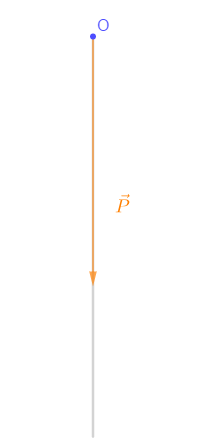
$-\ \ $ Point d'application : le point considéré (point $O$)
$-\ \ $ Sens : du haut vers le bas
$-\ \ $ Direction : verticale
$-\ \ $ Intensité : $||\vec{P}||=P=750\;N$
2) Faisons la représentation vectorielle du poids de cet objet à l'échelle de $1\;cm$ pour $150\;N.$
Exercice 4
Complétons le tableau suivant en calculant la grandeur qui manque dans chaque colonne :
On rappelle que : $P=m.g$
Et on tire : $m=\dfrac{P}{g}\quad\text{et}\quad g=\dfrac{P}{m}$
$$\begin{array}{|c|c|c|c|c|c|}\hline P&15\;N&19.6\;daN&3.924\;N&2.4\;kN&46.944\;kN\\ \hline m&1.5\;kg&20\;kg&400\;g&240\;kg&4.8\;t\\ \hline g(N.kg^{-1})&10&9.8&9.81&10&9.78\\ \hline\end{array}$$
Exercice 5
Le poids d'un objet $A$ est représenté par un vecteur de longueur $5\;cm$ à l'échelle de $1\;cm$ pour $30\;N.$
1) Calculons l'intensité $\|\vec{P}_{_{A}}\|$, du poids de $A.$
Comme $1\;cm$ représente $30\;N$ alors, $5\;cm$ vont représenter $5\times 30\;N$
Soit : $\boxed{\|\vec{P}_{_{A}}\|=150\;N}$
En effet,
$$\begin{array}{rcl} 1\;cm&\longrightarrow&30\;N\\ 5\;cm&\longrightarrow&\|\vec{P}_{_{A}}\|\end{array}$$
Donc, en utilisant la règle de proportionnalité, on obtient :
$$\dfrac{\|\vec{P}_{_{A}}\|}{30\;N}=\dfrac{5\;cm}{1\;cm}\ \Rightarrow\ \|\vec{P}_{_{A}}\|=5\times 30\;N$$
2) Calculons la masse $m_{_{A}}$, de $A$
On sait que : $\|\vec{P}_{_{A}}\|=m_{_{A}}.g$
Ce qui entraîne : $m_{_{A}}=\dfrac{\|\vec{P}_{_{A}}\|}{g}$
Or, $g=10\;N.kg^{-1}$ donc, $m_{_{A}}=\dfrac{150}{10}=15$
Ainsi, $\boxed{m_{_{A}}=15\;kg}$
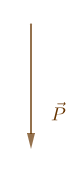
Exercice 6
1) Le poids d'un objet $B$ a pour intensité $840\;N.$
Déterminons l'échelle utilisée. soit : $1\;cm$ pour $x\;N$
Le poids de l'objet $B$ étant représenté par un vecteur de longueur $4.2\;cm$ alors, on peut écrire :
$$\begin{array}{rcl} 4.2\;cm&\longrightarrow&840\;N\\ 1\;cm&\longrightarrow&x\;N\end{array}$$
Ce qui donne : $\dfrac{x}{840}=\dfrac{1}{4.2}$
Donc, $x=\dfrac{1\times 840}{4.2}=200$
D'où, l'échelle utilisée est :
$$1\;cm\longrightarrow 200\;N$$
2) Un poids d'intensité $2500\;mN$ est représenté par le vecteur ci-dessous.
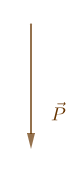
Déterminons l'échelle utilisée pour représenter ce poids.
En mesurant la longueur de ce vecteur, on trouve : $2.5\;cm$
Donc, $2.5\;cm$ vont représenter $2500\;mN$ ; ce qui veut dire que $1\;cm$ représente $\dfrac{2500}{2.5}\;mN.$ Soit : $1000\;mN$
Ainsi, l'échelle utilisée pour représenter ce poids est donnée par :
$$1\;cm\longrightarrow 1000\;mN=1\;N$$
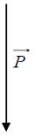
Exercice 7
1) Calculons l'intensité du poids d'un objet de masse $m=350\;kg$
On a : $P=m\times g$ avec $g=10\;N.kg^{-1}$
A.N : $P=350\times 10=3500$
D'où, $\boxed{P=3500\;N}$
2) Représentons le poids de cet objet.
En prenant comme échelle $1\;cm$ pour $1000\;N$, le poids sera alors représenté par un vecteur de longueur $x=\dfrac{3500}{1000}=3.5\;cm$

Exercice 8
$-\ $ En un lieu, l'intensité du poids d'un objet $A$ de masse $6\;kg$ est de $58.74\;N$
$-\ $ En ce lieu, un objet $B$ a un poids d'intensité $19.58\;N$
Calculons la masse de l'objet $B$
On a : $P_{_{B}}=m_{_{B}}\times g$
Donc, $m_{_{B}}=\dfrac{P_{_{B}}}{g}\quad(*)$
Or, $g$ est une constante qu'on peut déterminer en utilisant les données de l'objet $A.$
Ainsi, on a : $P_{_{A}}=m_{_{A}}\times g$
Ce qui donne : $g=\dfrac{P_{_{A}}}{m_{_{A}}}\quad(**)$
Pour l'objet $B$, on a : $P_{_{B}}=m_{_{B}}\times g$
Ce qui entraîne : $m_{_{B}}=\dfrac{P_{_{B}}}{g}$
Par suite, en remplaçant dans la relation (*), l'expression de $g$ donnée par la relation (**), on obtient :
$$m_{_{B}}=\dfrac{P_{_{B}}}{\dfrac{P_{_{A}}}{m_{_{A}}}}=\dfrac{P_{_{B}}\times m_{_{A}}}{P_{_{A}}}$$
A.N : $m_{_{B}}=\dfrac{19.58\times 6}{58.74}=2$
Ainsi, $\boxed{m_{_{B}}=2\;kg}$
Exercice 9
Un astronaute a une masse de $70\;kg$ sur terre.
1) Déterminons sa masse $(m_{_{\text{(sur lune)}}})$ sur la lune
Comme la masse d'un corps est constante quelque soit l'endroit ou l'espace qu'il se trouve alors,
$$m_{_{(\text{sur lune})}}=m_{_{(\text{sur terre})}}=70\;kg$$
2) Calculons l'intensité de son poids sur la lune.
On a : $P_{_{(\text{sur lune})}}=m_{_{(\text{sur lune})}}\times g_{_{(\text{sur lune})}}$
avec $g_{_{(\text{sur lune})}}=1.6\;N\cdot kg^{-1}$
A.N : $P_{_{(\text{sur lune})}}=70\times 1.6=112$
D'où, $\boxed{P_{_{(\text{sur lune})}}=112\;N}$
Exercice 10
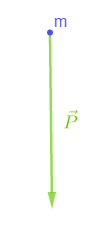
Le poids d'un objet est représenté par le vecteur ci-dessous :
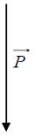
Calculons son intensité si l'échelle utilisée est de $1\;cm$ pour $150\;N$
En mesurant le vecteur, on trouve : $2.5\;cm$
Or, d'après l'échelle utilisée, $1\;cm$ représente $150\;N.$
Par suite, $2.5\;cm$ vont représenter $150\;N\times 2.5=375\;N$
D'où, $\boxed{P=375\;N}$
Exercice 11 Maitrise de connaissances
Recopions et complétons les phrases suivantes par les mots :
$N.Kg^{-1}$, un vecteur, varie, l'origine, $P=m.g$, newton, la Terre, centre de gravité, de haut en bas, verticale, l'attraction.
Le poids d'un corps est l'attraction exercée par la Terre sur ce corps.
Le poids d'un corps peut être modélisé par un vecteur de direction verticale dont le sens est de haut en bas. Par convention, on place l'origine de ce vecteur au centre de gravité du corps.
La relation entre la valeur du poids $P$ d'un corps et sa masse $m$ s'écrit : $P=m.g$
L'intensité de la pesanteur $g$ se mesure en $N.Kg^{-1}$ dans le système International et varie avec le lieu.
Exercice 12 Vrai ou Faux
Mettons vrai (V) ou faux (F) devant chaque proposition.
1) La direction du poids est oblique.$\quad(F)$
2) le point d'application du poids d'un corps est le centre de gravité de ce dernier.$\quad(V)$
3) la valeur du poids d'un objet se mesure avec une balance.$\quad(F)$
4) la relation entre le poids et la masse est $m=\dfrac{P}{m}\quad(F)$
5) le sens du poids est du bas vers le haut.$\quad(F)$
6) L'ordre de $g$ est de $10\;N.kg^{-1}\quad(V)$
Exercice 13 Utilisation de la bonne unité
Corrigeons les erreurs observées :
$-\ $ sur une boite de sucre : "masse nette : $1\;kg$"
En effet, l'unité de masse est le kilogramme $(kg)$ et l'unité de poids, le Newton $(N).$
Comme une boite de sucre pèse $1\;kg$ alors, au lieu de "poids net" on doit mettre "masse nette".
$-\ $ sur une plaque de chocolat : "Masse $125\;g$"
$-\ $ sur un véhicule utilitaire : "Poids à vide $1520\;N$"
En effet l'unité du poids étant le Newton $(N)$ donc, à la place de $kg$ on mettra $N.$
Exercice 14 Relation poids et masse
Un élévateur peut soulever des objets dont le poids ne dépasse pas $5000\;N.$
Déterminons la masse $(m)$ qui correspond à cette charge maximale
On sait que le poids maximal que l'élévateur peut soulever est : $P=5000\;N$
Ce poids va donc correspondre à une charge maximale de masse $m$ telle que :
$$P=m.g$$
Par suite, $m=\dfrac{P}{g}$ avec $g=9.8\;N.kg^{-1}$
A.N : $m=\dfrac{5000}{9.8}=510.2$
Ainsi, $\boxed{m=510.2\;kg}$
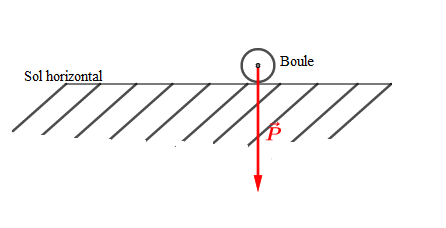
Exercice 15 Schématisation
Une boule repose sur un sol horizontal. La valeur de son poids est de $5\;N.$
Représentons le poids $\vec{P}$ de la boule en choisissant comme échelle : $1\;cm$ pour $2\;N.$
Pour cela, on doit trouver la longueur $x$ du vecteur représentant ce poids.
Comme $1\;cm$ représente $2\;N$ alors, on a :
$$\begin{array}{rcl} 1\;cm&\longrightarrow&2\;N\\x\;cm&\longrightarrow&5\;N\end{array}$$
Ce qui donne : $\dfrac{x}{1}=\dfrac{5}{2}=2.5$
Par suite, $x=2.5\;cm$
D'où, le poids de la boule sera représenté par un vecteur dirigé vers le bas et de longueur $2.5\;cm.$

Exercice 16 Distinction poids et masse
Fatou a une masse $m=60\;kg.$
1) Calculons son poids $(P_{_{T}})$ sur Terre.
On a : $P_{_{T}}=m.g_{_{T}}$ avec $g_{_{T}}=9.8\;N.kg^{-1}$
A.N : $P_{_{T}}=60\times 9.8=588$
Ainsi, $\boxed{P_{_{T}}=588\;N}$
2) Déterminons sa masse $(m_{_{L}})$ sur la Lune
La masse étant une grandeur physique constante alors :
$$m_{_{L}}=m$$
D'où, $\boxed{m_{_{L}}=60\;kg}$
3) Son poids $(P_{_{L}})$ sur la Lune est donné par :
$$P_{_{L}}=m_{_{L}}.g_{_{L}}$$
avec $g_{_{L}}=1.6\;N.kg^{-1}$
A.N : $P_{_{L}}=60\times 1.6=96$
Donc, $\boxed{P_{_{L}}=96\;N}$
4) Comparons le poids terrestre et le poids lunaire de Fatou.
On a : $P_{_{T}}=588\;N\ $ et $\ P_{_{L}}=96\;N$
Comme $588>96$ alors, $P_{_{T}}>P_{_{L}}$
Ce qui veut dire que le poids terrestre de Fatou est supérieur à son poids lunaire.
On peut aussi dire que le poids d'une masse quelconque est plus important sur Terre que sur la Lune.
Exercice 18
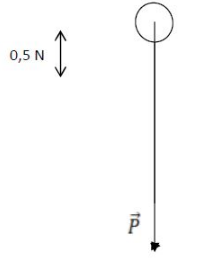
Déterminons les caractéristiques du poids $\vec{P}$ de l'objet $A$ représenté ci-dessous

$-\ $ Point d'application : centre de gravité de l'objet $A$
$-\ $ Sens : du haut vers le bas
$-\ $ Direction : verticale
$-\ $ Intensité : $||\vec{P}||=2.25\;N$
En effet, par mesure, on obtient comme échelle : $1\;cm$ pour $0.5\;N$
De plus, la mesure du vecteur $\vec{P}$ donne : $4.5\;cm$
Donc, on a :
$$\begin{array}{rcl} 1\;cm&\longrightarrow&0.5\;N\\4.5\;cm&\longrightarrow&\|\vec{P}\|\end{array}$$
Par suite, $\dfrac{4.5}{1}=\dfrac{\|\vec{P}\|}{0.5}$
Ce qui donne : $\|\vec{P}\|=4.5\times 0.5=2.25$
D'où, $\|\vec{P}\|=2.25\;N$

Commentaires
Malick Ndiaye (non vérifié)
lun, 02/17/2020 - 14:45
Permalien
Très intéressant
Malick Ndiaye (non vérifié)
lun, 02/17/2020 - 14:46
Permalien
Exercices physiques chimie
Anonyme (non vérifié)
mar, 03/22/2022 - 21:44
Permalien
Très intéressant
Faye Abdoulaye (non vérifié)
lun, 03/02/2020 - 11:24
Permalien
Remerciement
Nacanabo (non vérifié)
mer, 03/24/2021 - 10:22
Permalien
Enseigné
Anonyme (non vérifié)
jeu, 04/08/2021 - 14:06
Permalien
Vraiment depuis que j'ai
Anonyme (non vérifié)
mer, 06/23/2021 - 21:26
Permalien
moi aussi c est vraiment
Anonyme (non vérifié)
mer, 06/23/2021 - 21:28
Permalien
depuis que j ai decouverte
Fatou Mbaye (non vérifié)
sam, 04/17/2021 - 02:22
Permalien
Facilite le travail
Mens (non vérifié)
jeu, 04/22/2021 - 11:46
Permalien
Salut
Dieynaba souane (non vérifié)
ven, 03/15/2024 - 21:54
Permalien
Justifier
Awa (non vérifié)
ven, 05/09/2025 - 22:56
Permalien
De me rendre des services
anonyme (non vérifié)
mar, 05/25/2021 - 00:35
Permalien
ok
Anonyme (non vérifié)
jeu, 07/15/2021 - 22:36
Permalien
Excellent
Anonyme (non vérifié)
jeu, 01/20/2022 - 20:19
Permalien
Pourquoi les devoirs de PC et
Maty (non vérifié)
dim, 05/08/2022 - 20:31
Permalien
Réussir
Yacine Diallo (non vérifié)
dim, 05/15/2022 - 22:13
Permalien
Pc
Alassane ba (non vérifié)
jeu, 06/09/2022 - 20:02
Permalien
Domade d aide
sunshine (non vérifié)
dim, 06/19/2022 - 15:50
Permalien
Perfect
Skywalker (non vérifié)
ven, 03/15/2024 - 22:33
Permalien
Ces exercices m'ont permis de
Diary sow (non vérifié)
ven, 05/10/2024 - 20:10
Permalien
Faire exo56
Fatou Seye (non vérifié)
lun, 03/10/2025 - 22:04
Permalien
Pc
Ajouter un commentaire