Solution des exercices : La loi d'Ohm 3e
Classe:
Troisième
Exercice 1
1) Trouvons la résistance du fil chauffant.
On a : $P=R\times I^{2}\ \Rightarrow\ R=\dfrac{P}{I^{2}}$
A.N : $R=\dfrac{500}{4^{2}}=31.25$
Donc, $$\boxed{R=31.25\;\Omega}$$
2) Calculons la tension à ses bornes.
On a : $U=R\times I$
A.N : $U=31.25\times 4=125$
Donc, $$\boxed{U=125\;V}$$
Exercice 2
1) Calcul de la tension
On a : $U=R\times I$
A.N : $U=47\times 0.12=5.64$
Donc, $$\boxed{U=5.64\;V}$$
2) Calculons l'intensité du courant qui traverse le conducteur, sachant que la tension à ses bornes a été doublée.
Soit : $U'=R.I'$
Or, $\ U'=2U$ donc en remplaçant $U'$ par $2U$, on obtient : $2U=R.I'$
Par suite, $\dfrac{2U}{R}=I'$
Comme $\dfrac{U}{R}=I$ alors,
$$I'=2I$$
A.N : $I'=2\times 0.12=0.24$
Donc, $$\boxed{I'=0.24\;A}$$
Exercice 3
1) Trouvons la valeur de la résistance.
On a : $U=R\times I\ \Rightarrow\ R=\dfrac{U}{I}$
A.N : $R=\dfrac{6}{160\;10^{-3}}=37.5$
Donc, $$\boxed{R=37.5\;\Omega}$$
2) La puissance électrique consommée est de :
$P=R\times I^{2}$
A.N : $P=37.5\times(160\;10^{-3})^{2}=0.96$
Donc, $$\boxed{P=0.96\;W}$$
Exercice 4
1) Signification de ces indications :
$6\;V$ : la tension électrique
$1\;W$ : la puissance électrique
2) Calculons l'intensité du courant qui traverse la lampe quand elle fonctionne normalement.
On a : $P=R.I^{2}=R\times I\times I$
Or, $\ R.I=U$ donc, $P=U.I$
Ce qui donne : $I=\dfrac{P}{U}$
A.N : $I=\dfrac{1}{6}=0.166$
Donc, $$\boxed{I=0.166\;A}$$
3) Calculons la valeur de la résistance.
On a : $R=\dfrac{U}{I}$
A.N : $R=\dfrac{6}{0.166}=36.14$
Donc, $$\boxed{R=36.14\;\Omega}$$
4) $R\text{ (à chaud) }=36.14\;\Omega\;,\ R\text{ (à froid) }=8\;\Omega.$
La résistance augmente avec la température.
Exercice 5 Caractéristique d'un conducteur ohmique
1) Caractéristique intensité - tension de ce conducteur.
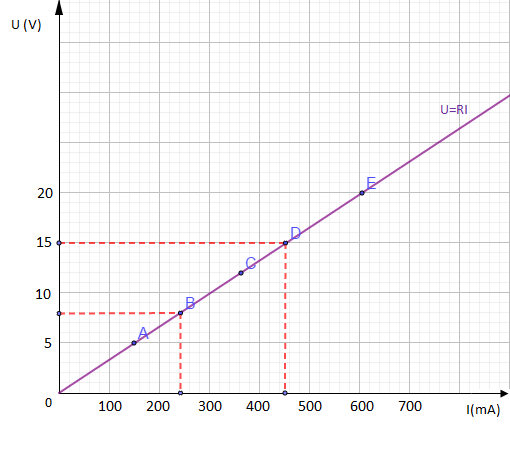
$\begin{array}{rcl}\text{Echelle }\ :\ 1\;cm&\longrightarrow&100\;mA \\ 1\;cm&\longrightarrow&5\;V\end{array}$
2) Déduisons de cette courbe la valeur de la résistance du conducteur.
La courbe représentative est une application linéaire $(U=RI)$ de coefficient linéaire $R.$
Soit $B$ et $D$ deux points de cette droite.
Alors, on a :
$R=\dfrac{y_{D}-y_{B}}{x_{D}-x_{B}}=\dfrac{3-1.6}{4.53-2.43}=\dfrac{1.4}{2.1}=066$
Donc, $$\boxed{R=0.66\;\Omega}$$
Exercice 6
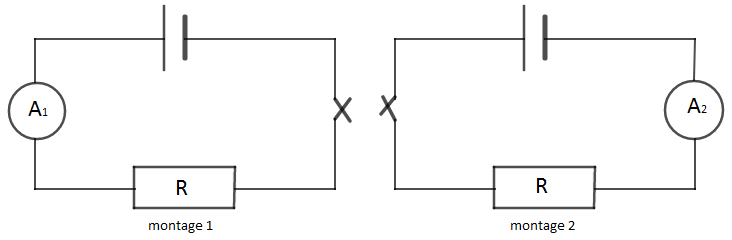
1) D'après les montages ci-dessus, l'ampèremètre $A_{1}$ donne le même indicateur $(320\;mA)$ que l'ampèremètre $A_{2}$ car le circuit est en série.
2) Donnons la valeur de la résistance $R$ si la tension de la pile vaut $6\;V$.
On a : $U=R\times I\ \Rightarrow\ R=\dfrac{U}{I}$
A.N : $R=\dfrac{6}{320\;10^{-3}}=18.75$
Donc, $$\boxed{R=18.75\;\Omega}$$
Exercice 7
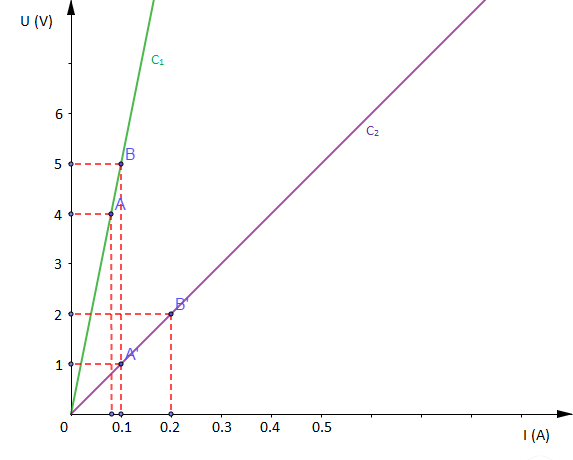
$\begin{array}{rcl}\text{Echelle }\ :\ 1\;cm&\longrightarrow&0.1\;A \\ 1\;cm&\longrightarrow&1\;V\end{array}$
1) D'après le graphique ci-dessus, nous constatons que les représentations $C_{1}$ et $C_{2}$ sont des droites et donc des applications linéaires de coefficient linéaire respectif $R_{1}$ et $R_{2}.$
Or, nous remarquons que $C_{1}$ est au dessus de $C_{2}$, donc cela signifie que coefficient linéaire de $C_{1}$ est supérieur au coefficient linéaire $C_{2}.$
Ainsi, on a : $R_{1}>R_{2}$
2) Donnons la valeur de la résistance $R_{1}$
La représentation de $C_{1}$ étant une droite de coefficient linéaire respectif $R_{1}$, alors en prenant deux points $A$ et $B$ de cette droite on obtient :
$R_{1}=\dfrac{y_{B}-y_{A}}{x_{B}-x_{A}}=\dfrac{5-4}{0.1-0.08}=\dfrac{1}{0.02}=50$
D'où $$\boxed{R_{1}=50\;\Omega}$$
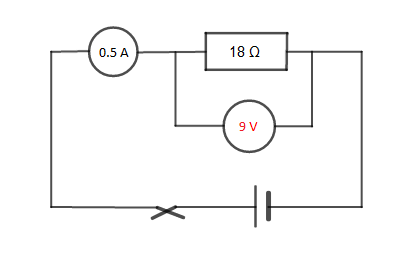
Exercice 8
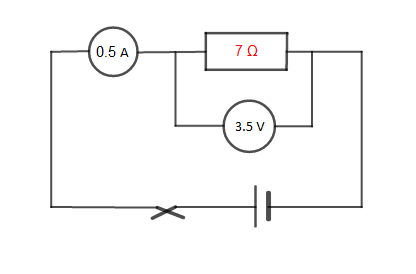
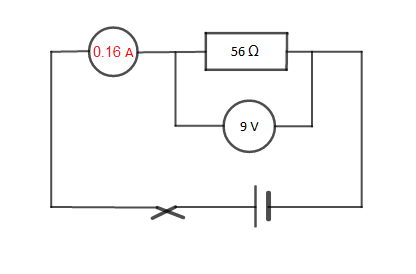
Indiquons la valeur manquante dans chacun des cas suivants
$R_{1}=\dfrac{3.5}{0.5}=7\;\Omega$

$I_{2}=\dfrac{9}{56}=0.16\;A$

$U_{3}=18\times 0.5=9\;V$

Exercice 9 Loi d'Ohm
1) Énonçons la loi d'Ohm : La tension $U$ aux bornes d'un conducteur Ohmique est égale au produit de sa résistance $R$ par l'intensité $I$ du courant qui le traverse.
2) La relation entre $U\;,\ I\ $ et $\ R$ est donnée par : en précisant les unités :
$$U=R\times I$$
avec $U$ en volt $(V)\;,\ R$ en Ohm $(\Omega)$ et $I$ en ampère $(A)$
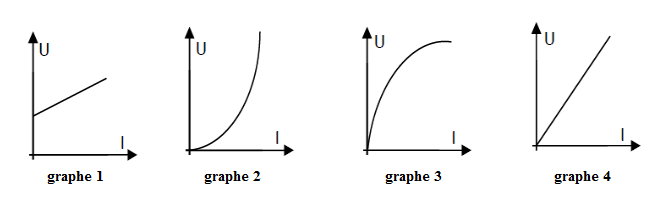
3) Considérons les graphes ci-dessous :

On sait que la relation entre $U\;,\ I\ $ et $\ R$, donnée par $U=R\times I$, traduit une relation linéaire qui peut être représentée par une droite passant par l'origine du repère.
Donc, c'est le graphe $n^{\circ}4$ qui correspond à la relation entre $U\;,\ I\ $ et $\ R$ dans le cas d'un conducteur ohmique.
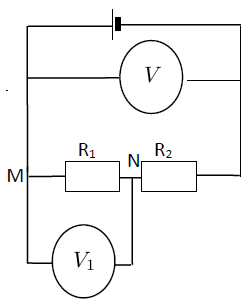
Exercice 10
On considère le schéma du montage suivant appelé pont diviseur de tension.

$U_{e}$ mesurée par le voltmètre $V$ est appelée tension d'entrée et $U_{s}$ mesurée par $V_{1}$ tension de sortie.
1) Montrons que $\dfrac{U_{s}}{U_{e}}=\dfrac{R_{1}}{(R_{1}+R_{2})}$
Soit : $U_{1}$ la tension aux bornes de $R_{1}$ et $U_{2}$ celle aux bornes de $R_{2}.$
$R_{1}\ $ et $\ R_{2}$ sont montées en série or, la tension aux bornes d'un groupement en série est égale à la somme des tensions.
Donc, $U_{e}=U_{1}+U_{2}\ $ avec : $U_{1}=R_{1}.I\ $ et $\ U_{2}=R_{2}I$ d'après la loi d'Ohm.
Par suite, $U_{e}=R_{1}.I+R_{2}.I=(R_{1}+R_{2})I$
De plus, $V_{1}$ mesure en même temps la tension de sortie $(U_{s})$ et la tension aux bornes de $R_{1}.$
Donc, $U_{s}=U_{1}=R_{1}.I$
Ainsi, $\dfrac{U_{s}}{U_{e}}=\dfrac{R_{1}.I}{(R_{1}+R_{2})I}$
D'où, $\boxed{\dfrac{U_{s}}{U_{e}}=\dfrac{R_{1}}{(R_{1}+R_{2})}}$
2) Calculons la tension $(U_{s})$ à la sortie entre les points $M\ $ et $\ N$
On sait que : $\dfrac{U_{s}}{U_{e}}=\dfrac{R_{1}}{(R_{1}+R_{2})}$
Ce qui donne alors : $U_{s}=\dfrac{R_{1}\times U_{e}}{(R_{1}+R_{2})}$
avec $R_{1}=60\;\Omega\;;\ R_{2}=180\;\Omega\ $ et $\ U_{e}=12\;V$
A.N : $U_{s}=\dfrac{60\times 12}{(60+180)}=3$
D'où, $$\boxed{U_{s}=3\;V}$$
3) Rôle d'un pont diviseur de tension :
Le pont diviseur de tension est un montage électronique simple permettant de diviser une tension d'entrée afin de créer une tension qui soit proportionnelle à cette tension d'entrée.
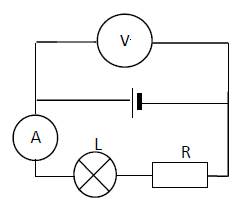
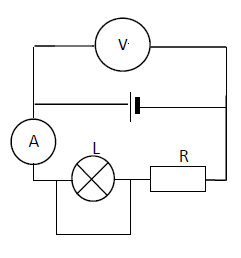
Exercice 11
On monte en série un générateur fournissant une tension constante $U=6.4\;V$, un résistor de résistance $R=10\;\Omega$ et une lampe $L.$
L'intensité du courant $I=0.25\;A$

1) Calculons la tension $U_{1}$ entre les bornes du résistor $R.$
D'après la loi d'Ohm, on a : $U_{1}=R.I$
A.N : $U_{1}=10\times 0.25=2.5$
D'où, $$\boxed{U_{1}=2.5\;V}$$
2) Calculons la tension $U_{2}$ entre les bornes de la lampe.
Le résistor et la lampe étant montés en série alors, la tension aux bornes de l'ensemble est égale à la somme des tensions.
Donc, $U=U_{1}+U_{2}$
Par suite, $U_{2}=U-U_{1}$
A.N : $U_{2}=6.4-2.5=3.9$
Ainsi, $$\boxed{U_{2}=3.9\;V}$$
3) On place un fil de connexion en dérivation aux bornes de la lampe.

Lorsqu'on place un fil de connexion de résistance nulle en dérivation aux bornes de la lampe alors, le courant passe par le chemin le plus facile à franchir ; le fil.
Par conséquent, aucun courant ne passe par la lampe.
D'où : $U_{2}=0\;V$
4) Comme aucun courant ne traverse la lampe alors, $I_{_{L}}=0\;A$ et donc, la lampe ne brille pas.
5) Calculons l'intensité du courant qui traverse la résistance.
Le fil de connexion étant placé en dérivation aux bornes de la lampe alors, d'après la loi des nœuds, on a :
$$I_{_{L}}+I_{_{\text{fil}}}=I_{_{R}}$$
Or, $I_{_{L}}=0\ $ et $\ I_{_{\text{fil}}}=I$
Donc, $I_{_{R}}=I_{_{\text{fil}}}=I$
D'où, $$\boxed{I_{R}=0.25\;A}$$

Commentaires
racine (non vérifié)
sam, 06/29/2019 - 16:35
Permalien
telecharge
Coura Dieng (non vérifié)
mar, 06/11/2024 - 00:01
Permalien
Apprendre et réussir
Aziz rayan (non vérifié)
mar, 05/26/2020 - 22:10
Permalien
Formation
Dieye (non vérifié)
dim, 06/19/2022 - 11:27
Permalien
Apprendre
Dieye (non vérifié)
dim, 06/19/2022 - 11:27
Permalien
Apprendre
Anonyme (non vérifié)
lun, 06/01/2020 - 14:30
Permalien
Syper
ANONYME (non vérifié)
mer, 09/02/2020 - 22:16
Permalien
Super c'est très intéressant.
Anonyme (non vérifié)
ven, 09/04/2020 - 20:40
Permalien
Vous nous aidez vraiment
Peter (non vérifié)
mer, 10/07/2020 - 20:39
Permalien
Aide
Peter (non vérifié)
mer, 10/07/2020 - 20:40
Permalien
Aide
Queen (non vérifié)
dim, 03/14/2021 - 15:37
Permalien
C est super pour réviser
Wijdan (non vérifié)
sam, 05/15/2021 - 13:44
Permalien
Des exercices déficile un peu
8906877646765876767 (non vérifié)
sam, 05/21/2022 - 17:16
Permalien
bg
Lonatoubap (non vérifié)
ven, 04/28/2023 - 22:32
Permalien
Super site et appli
Lonatoubap (non vérifié)
ven, 04/28/2023 - 22:32
Permalien
Super site et appli
Ibnoul khatib Ilhame (non vérifié)
mar, 05/30/2023 - 18:51
Permalien
Objection sur l'exercice N°11
Marietou (non vérifié)
mar, 05/30/2023 - 21:16
Permalien
Exercice 11
Anonyme (non vérifié)
ven, 06/07/2024 - 19:59
Permalien
merci pour votre information
Bradley (non vérifié)
dim, 03/16/2025 - 19:23
Permalien
Apprendre
Camara Youssouf... (non vérifié)
lun, 06/09/2025 - 13:56
Permalien
Recherche
Lilya (non vérifié)
dim, 01/25/2026 - 11:01
Permalien
tres bons exercices pour
Ajouter un commentaire