Solution des exercices : Force et champ électrostatiques - 1er s
Classe:
Première
Exercice 1 : pendule et force électrostatique
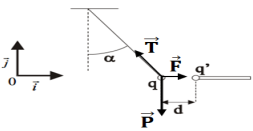
1. Bilan des forces qui s'exercent sur la bille et représentation de ses forces
Les forces qui s'exercent sur la bille sont : Le poids $\overrightarrow{P}$, la force électronique $\overrightarrow{F}$ et la tension $\overrightarrow{T}$
2. La solution d'équilibre s'écrit :
$\overrightarrow{P}+\overrightarrow{F}+\overrightarrow{T}=\overrightarrow{0}$
3. Détermination de l'intensité de la force électronique.
Suivant $\vec{i}$ et $\vec{j}$, la relation vectorielle devient :
$\begin{array}{rcl}0+F-T\sin\alpha&=&0\\\Rightarrow\;T\sin\alpha&=&F\quad(1) \end{array}$
$\begin{array}{rcl} -mg+0+T\cos\alpha&=&0\\\Rightarrow\;T\cos\alpha&=&mg\quad (2) \end{array}$
$\begin{array}{rcl} (1)\text{et}(2)\tan\alpha&=&\dfrac{F}{mg}\\\Rightarrow\;F&=&mg\tan\alpha\\&=&20\cdot10^{-3}\times10\times20^{\circ}\\\Rightarrow\;F&=&7.3\cdot10^{-2}N \end{array}$
4. Détermination de la charge $q$ portée par la bille.
$\begin{array}{rcl} F&=&\dfrac{k|q|q'}{d}\\\Rightarrow\;|q|&=&\dfrac{Fd}{Kq'}\\\Rightarrow\;q&=&\dfrac{Fd}{Kq'}\\&=&\dfrac{7.3\cdot10^{-2}\times2\cdot10^{-2}}{9\cdot10^{9}\times10^{-6}}\\\Rightarrow\;q&=&-1.6\cdot10^{-7}C \end{array}$
Exercice 2
1.1 Définition de la ligne de champ.
Une ligne de champ est une courbe tangente en tout point au vecteur champ électrostatique.
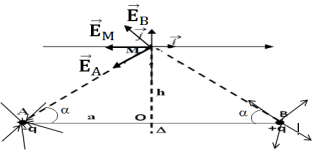
Représentation su spectre électronique des deux deux charges placées en $A$ et $B$. (Voir figure)
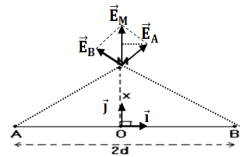
1.2 Représentation des vecteurs champs électriques $\overrightarrow{E}_{A}$ et $\overrightarrow{E}_{B}$ crées par $B_{1}$ et $B_{2}$ au point $M.$ (Voir figure)
1.3 Expression de la vecteur de $E_{A}$ et de $E_{B}$ en fonction de $K$, $q$, $a$ et $h.$
Montrons que $E_{A}=E_{B}$
$\begin{array}{rcl} E_{A}&=&K\dfrac{|-q|}{AM^{2}}\\&=&K\dfrac{|q|}{AM^{2}}\text{ or }AM^{2}=AO^{2}+OM^{2}\text{ et }|-q|=q\\\Rightarrow\;AM^{2}&=&a^{2}+h^{2}\\\Rightarrow\;E_{A}&=&K\dfrac{q}{a^{2}+h^{2}}\quad(1) \end{array}$
$\begin{array}{rcl} E_{B}&=&K\dfrac{q}{BM^{2}}\\&=&K\dfrac{|q|}{BM^{2}}\text{ or }BM^{2}=BO^{2}+OM^{2}\\\Rightarrow\;BM^{2}&=&a^{2}+h^{2}\\\Rightarrow\;E_{B}&=&K\dfrac{q}{a^{2}+h^{2}}\quad(2) \end{array}$
$(1)$ et $(2)\Rightarrow\;E_{A}=E_{B}$
$K=9\cdot10^{9}u\cdot\;s\cdot\;i$
2.1 Détermination des coordonnées $E_{Mx}$ et $E_{My}$ du vecteur $\overrightarrow{E_{M}}$ en fonction de $K$, $q$ $a$ et $h$
$\begin{array}{rcl} \overrightarrow{E_{M}}=\overrightarrow{E_{A}}+\overrightarrow{E_{B}}&\Rightarrow&\left\lbrace\begin{array}{lcl} E_{Mx}&=&E_{Ax}+E_{Bx}\\ E_{My}&=&E_{Ay}+E_{By} \end{array}\right.\\&\Rightarrow&\left \lbrace\begin{array}{lcl} E_{Mx}&=&-E_{A}\cos\alpha-E_{B}\cos\alpha\\ E_{My}&=&E_{A}\sin\alpha-E_{B}\sin\alpha \end{array}\right.\\\text{ comme }E_{A}=E_{B}&\Rightarrow&\left\lbrace\begin{array}{lcl} E_{Mx}&=&-2E_{A}\cos\alpha\\ E_{My}&=&0 \end{array}\right. \end{array}$
2.2 Montrons que $\overrightarrow{E_{M}}=-\dfrac{2K|q|\cos\alpha}{\left(a^{2}+h^{2}\right)}\vec{i}$, avec $\cos\alpha=\dfrac{\alpha}{\sqrt{a^{2}+h^{2}}}$
$\begin{array}{rcl} E_{M}&=&E_{Mx}\vec{i}+E_{My}\vec{j}\\\Rightarrow\overrightarrow{E_{M}}&=&-2E_{A}\cos\alpha\vec{i}+0\vec{j}\\\Rightarrow\overrightarrow{E_{M}}&=&-2E_{A}\cos\vec{i}\text{ or }E_{A}=K\dfrac{|q|}{\left(a^{2}+h^{2}\right)}\\\Rightarrow\overrightarrow{E_{M}}&=&-\dfrac{2K|q|}{\left(a^{2}-h^{2}\right)}\cos\alpha\vec{i} \end{array}$
2.3 Déduction de la valeur de $\overrightarrow{E}_{M}$ au point $O$
$\begin{array}{rcl} E_{M}&=&\dfrac{2K|q|}{\left(a^{2}+h^{2}\right)}|\cos\alpha|\text{ or }\cos\alpha=\dfrac{a}{\sqrt{a^{2}+h^{2}}}\\\Rightarrow\;E_{M}&=&\dfrac{2K|q|}{\left(a^{2}+h^{2}\right)}\dfrac{a}{\sqrt{a^{2}+h^{2}}} \end{array}$
$\begin{array}{rcl}\text{En }O\;,\ h=0\Rightarrow\;E_{M}&=&\dfrac{2K|q|}{\left(a^{2}+0^{2}\right)}\dfrac{a}{\sqrt{a^{2}+0^{2}}}\\\Rightarrow\;E_{M}&=&\dfrac{2K|q|}{a^{2}}\\&=&\dfrac{2\times9\cdot10^{9}\times0.3\cdot10^{-6}}{\left(10\cdot10^{-2}\right)^{2}}\\\Rightarrow\;E_{M}&=&5.4\cdot10^{5}N\cdot C^{-1} \end{array}$
Exercice 3
1. Énoncé la loi de Coulomb
Deux corps ponctuels $A$ et $B$, de charges respectives $q_{A}$ et $q_{B}$, exercent l'un sur l'autre des forces d'attraction ou de répulsion directement opposées, dirigées suivant la droite $(AB)$, de valeur proportionnelles aux deux charges et inversement proportionnelles au carré de la distance qui les sépare
2.1 Détermination des caractéristiques de la force exercée par $A$ sur $B$ et la force exercée par $B$ sur $A.$
$-\ $Point d'application : les charges
$-\ $Direction : la droite $AB$ qui joint les deux charges
$-\ $Sens : les charges $q_{A}$ et $q_{B}$ sont de signe contraires, le produit $q_{A}\times q_{B}$ est négatif et $\overrightarrow{F_{A/B}}$ est dirigée suivant $\overrightarrow{u_{AB}}(\text{ de }B\text{ vers }A)$
De même $\overrightarrow{u}_{B/A}$ est dirigée suivant $\overrightarrow{u}_{AB} (\text{ de }A \text{ vers }B).$
Les deux charges $s'$
$-\ $Intensité :
$\begin{array}{rcl} F_{B/A}&=&F_{A/B}\\&=&k\dfrac{|q_{A}||q_{B}|}{AB^{2}}\\&=&9.0\cdot10^{9}\dfrac{|-3\cdot10^{-9}||4\cdot10^{-9}|}{\left(10\cdot10^{-2}\right)^{2}}\\\Rightarrow \;F_{B/A}&=&F_{A/B}\\&=&1.1\cdot10^{-7}N \end{array}$
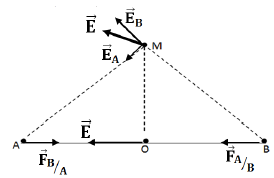
2.2 Représentation de $\overrightarrow{F}_{B/A}$ et $\overrightarrow{F}_{A/B}$
3. Détermination des caractéristiques du vecteur champ électrostatique $\overrightarrow{E}$ crée par ces deux charges électroniques et représentation du vecteur champ électronique
3.1. Au milieu $O$ de segment $AB.$
$-\ $Point, direction et sens : voir figure
$-\ $Intensité :
$\begin{array}{rcl} \overrightarrow{E_{o}}&=&\overrightarrow{E_{A}}+\overrightarrow{E_{B}}\\\Rightarrow\;E_{0}&=&E_{A}+E_{B}\\&=&\;k\dfrac{\left|q_{A}\right|}{AO^{2}}+k\dfrac{q_{B}}{BO^{2}}\text{ or }AO=BO\\\Rightarrow\;E_{o}&=&\dfrac{k}{OA^{2}}\left(\left|q_{A}\right|+q_{B}\right)\\\Rightarrow\;E_{o}&=&\dfrac{9.0\cdot10^{9}}{\left(5\cdot10^{-2}\right)^{2}}\left(\left|-3\cdot10^{-9}\right|+4\cdot10^{-9}\right)\\\Rightarrow\;E_{o}&=&12.6\cdot10^{4}N\cdot C^{-1} \end{array}$
3.2 En un point $M$ de la médiatrice de $AB$, situé à $5\,cm$ de $O$
$-\ $Point, direction et sens : voir figure
$-\ $Intensité :
$\begin{array}{rcl} \overrightarrow{E}_{M}&=&\overrightarrow{E}_{A}+\overrightarrow{E}_{B}\\\Rightarrow\;E_{M}&=&\sqrt{E_{A}^{2}+E_{B}^{2}}\\&=&\sqrt{\left(k\dfrac{|q_{A}|}{AM}_{2}\right)^{2}+\left(k\dfrac{q_{B}}{BM}^{2}\right)^{2}}\text{ or }AM^{2}=AO^{2}+OM^{2}\\&=&5^{2}+5^{2}\\&=&50\,cm^{2}\\\Rightarrow\;AM&=&5\sqrt{5\;cm}\ ;\ (BM=5\sqrt{5\,cm} \end{array}$
$\begin{array}{rcl} E_{M}&=&\sqrt{\left(k\dfrac{\left|q_{A}\right|}{AM^{2}}\right)^{2}+\left(k\dfrac{q_{B}}{BM^{2}}\right)^{2}}\\&=&\dfrac{k}{AM^{2}}\sqrt{\left|q_{A}\right|^{2}+q_{B}^{2}}\\\Rightarrow\;E_{M}&=&\dfrac{9.0\cdot 10^{9}}{\left(5\sqrt{5}\cdot10^{-2}\right)^{2}}\sqrt{\left|3\cdot10^{-9}\right|^{2}+\left(4\cdot10^{-9}\right)^{2}}\\\Rightarrow\;E_{M}&=&4.02\cdot10^{4}N\cdot C^{-1} \end{array}$
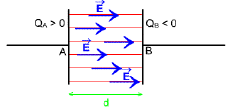
4. Les caractéristiques d'un champ électrique uniforme
Un champ électrique uniforme est un champ dont le vecteur champ électrique a même direction, même sens et même intensité en tout point de l'espace champ
Schéma de spectre de champ
Les lignes de champ sont des droites parallèles.
L'ensemble des lignes constitue le spectre électrique
Exercice 4
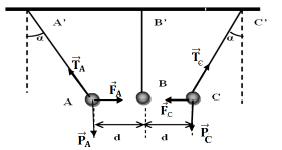
1. Le signe de $q'$ est positif car elle attirée par la charge $q$ qui de signe positif
2.1 Bilan des forces qui s'exercent sur $A$
Les forces qui s'exercent sur $A$ sont :
Le poids $\overrightarrow{P_{A}}$ ; la tension $\overrightarrow{T}_{A}$ et la force électrostatique $\overrightarrow{F_{A}}$
2.2 Représentation de ces forces (voir figure) sur un schéma,
2.3 Énoncé la condition d'équilibre de $A$
La sphère $A$ est en équilibre sous de ces trois forces ; la somme vectorielle de ces trois forces est nulle
$\overrightarrow{P_{A}}+\overrightarrow{T}_{A}+\overrightarrow{F_{_{A}}}=\overrightarrow{0}$
2.4 Déduction de la valeur de l'angle $\alpha$
$\begin{array}{rcl} \overrightarrow{P_{A}}+\overrightarrow{T}_{A}+\overrightarrow{F_{A}}=0&\Rightarrow&\left\lbrace\begin{array}{lcl} 0-T_{A}\sin\alpha+F_{A}&=&0\\ mg-T_{A}\cos\alpha+0&=&0 \end{array}\right.\\&\Rightarrow&\left\lbrace\begin{array}{lcl} T_{A}\sin\alpha&=&F_{A}\quad(1)\\ T_{A}\cos\alpha&=&mg\quad(2) \end{array}\right.\\(1)\text{ et }(2)\Rightarrow\tan\alpha&=&\dfrac{F_{A}}{mg}\\&=&\dfrac{kq\left|q'\right|}{mgd^{2}}\\&=&\dfrac{kq|-2q|}{mgd^{2}}\\\Rightarrow\tan\alpha&=&\dfrac{2Kq^{2}}{mgd^{2}}\\\Rightarrow\alpha&=&\tan^{-1}\alpha\\&=&\tan^{-1}\left(\dfrac{2Kq^{2}}{mgd^{2}}\right)\\&=&\tan^{-1}\left(\dfrac{2\times9.00\cdot10^{9}\times\left(200\cdot10^{-9}\right)^{2}}{10.0\cdot10^{-3}\times9.81\times\left(10.0\cdot10^{-2}\right)^{2}}\right)\\\Rightarrow\alpha&=&36.3^{\circ} \end{array}$
2.5 Détermination des valeurs des forces qui s'exercent sur $A.$
$\begin{array}{rcl} P_{A}&=&mg\\&=&10.0\cdot10^{-3}\times9.81\\\Rightarrow\;P_{A}&=&9.81\cdot10^{-3}N \end{array}$
$\begin{array}{rcl} mg-T_{A}\cos\alpha+0&=&0\\\Rightarrow\;T_{A}&=&\dfrac{P_{A}}{\cos\alpha}\\&=&\dfrac{9.81\cdot10^{-3}}{\cos36.3^{\circ}}\\\Rightarrow\;T_{A}&=&12.2\cdot10^{-3}N \end{array}$
$\begin{array}{rcl} F_{A}&=&\dfrac{2kq^{2}}{d^{2}}\\&=&\dfrac{2\times9.00\cdot10^{9}\times\left(200\cdot 10^{-9}\right)^{2}}{\left(10.0\cdot 10^{-2}\right)^{2}}\\ \Rightarrow\;F_{A}&=&72\cdot 10^{-3}N \end{array}$
3.1 Bilan des forces qui s'exercent sur $B.$
Les forces sur $B$ sont :
Le Poids $\overrightarrow{P_{B}}$, la tension du fil $\overrightarrow{T}_{B}$ et les forces électrostatiques $\overrightarrow{F}_{A/B}$ et $\overrightarrow{F}_{C/B}$ exercées respectivement par les sphères $A$ et $C$ sur la sphère $B$
3.2 Représentation de ces forces (voir figure) sur un schéma, sans souci d'échelle mais en respectant leurs
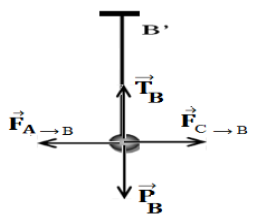
3.3 Détermination des valeurs des forces qui s'exercent sur $B.$
$\begin{array}{rcl} P_{B}&=&mg\\&=&10.0\cdot10^{-3}\times9.81\\\Rightarrow\;P_{B}&=&9.81\cdot10_{-3}N \end{array}$
$T_{B}=P_{B}=9.81\cdot10^{-3}N$
$\begin{array}{rcl} F_{A\longrightarrow\;B}&=&F_{C\longrightarrow\;A}\\&=&F_{A}\\\Rightarrow\;F_{A\longrightarrow\;B}&=&F_{C\longrightarrow\;A}\\&=&72.10\cdot^{-3}N \end{array}$
Exercice 5
1. Détermination des caractéristique du vecteur champ électrostatique
du vecteur champ électrostatique au point $C$
$-\ $Point, direction et sens : voir figure
$- $Intensité :
$\begin{array}{rcl} E_{A}&=&k\dfrac{\left|q_{1}\right|}{AO^{2}}\text{ or }AO=BO\\\Rightarrow\;E_{A}&=&\dfrac{k}{AC^{2}}\left(\left|q_{A}\right|+q_{B}\right)\\\Rightarrow\;E_{A}&=&\dfrac{9.0\cdot10^{9}\left|-10\cdot10^{-9}\right|}{\left(5\cdot10^{-2}\right)^{2}}\\\Rightarrow\;E&=&3.6\cdot10^{4}N\cdot C^{-1} \end{array}$
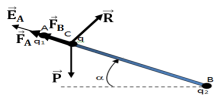
2.a. Bilan des forces qui s'exercent sur la sphère $(S)$ et représentation de ces forces (voir figure).
Les forces qui s'exercent sur la sphère sont :
Le poids,$\overrightarrow{P}$ ; la réaction $\overrightarrow{R}$ et les forces électrostatiques $\overrightarrow{F_{A}}$ et $\overrightarrow{B_{B}}$
b. Calcul de la masse $m$ et la valeur de la réaction de la tige.
La condition d'équilibre de la sphère s'écrire :
$\overrightarrow{P}+\overrightarrow{R}+\overrightarrow{F_{A}}+\overrightarrow{F_{B}}=\overrightarrow{0}$
Suivant le sens de $\overrightarrow{F_{A}}$ :
$\begin{array}{rcl}-P\sin\alpha+0+F_{A}+F_{B}&=&0\\\Rightarrow\;P\sin\alpha&=&F_{A}+F_{B}\\\Rightarrow\;mg\sin\alpha&=&k\dfrac{\left|q_{1}\right|q}{AC^{2}}+k\dfrac{q_{2}q}{BC^{2}}\\\Rightarrow\;m&=&k\dfrac{q_{2}q}{g\sin\alpha}\left(\dfrac{1}{AC^{2}}+\dfrac{1}{BC^{2}}\right)\\\Rightarrow\;m&=&9.0\cdot 10^{9}\times\dfrac{10\cdot 10^{-9}\times30\cdot 10^{-9}}{10\times\sin 30^{\circ}}\left(\dfrac{1}{\left(5\cdot 10^{-2}\right)^{2}}+\dfrac{1}{\left(15\cdot 10^{-2}\right)^{2}}\right)\\\Rightarrow\;m&=&2.4\cdot 10^{-4}kg \end{array}$
Suivant le sens de $\overrightarrow{R}$ :
$\begin{array}{rcl} -P\cos\alpha+R+0+0&=&0\\\Rightarrow\;R&=&P\cos\alpha\\\Rightarrow\;R&=&mg\cos\alpha\\&=&2.4\cdot10^{-4}\times10\cos30^{\circ}\\\Rightarrow\;R&=&2.1\cdot10^{-3}N \end{array}$
3. Lorsque la tige $AB$ est horizontale, la sphère ne reste plus immobile.
Elle se déplace vers la sphère $A$ à cause de l'action des deux forces électrostatiques
Exercice 6
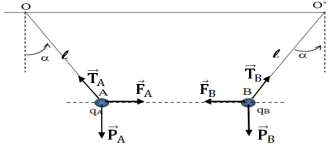
1. Calcul de la distance $AB$ à m'équilibre.
$\begin{array}{rcl} AB&=&OO'-2l\sin\alpha\\&=&14-\times0\cdot1\\\Rightarrow\;AB&=&10\;cm \end{array}$
2.1 Représentation de toutes les forces exercées sur les boules $A$ et $B$ (voir figure)
2.2 Détermination de la valeur de la force de l'interaction électrique existant entre es boules $A$ et $B.$
$\begin{array}{rcl} F_{AB}&=&\dfrac{Kq_{A}|q_{B}|}{AB^{2}}\\&=&\dfrac{9\cdot10^{9}\times2\cdot10^{-6}\times2\cdot10^{-6}}{\left(10\cdot10^{-2}\right)^{2}}\\\Rightarrow\;F_{AB}&=&3.6N \end{array}$
Exercice 7
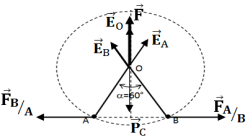
1. Représentation, des forces électrique $\overrightarrow{F}_{A/B}$ et $\overrightarrow{F}_{B/A}$ (Voir figure)
Caractéristique de $\overrightarrow{F}_{A/B}$
$\begin{array}{rcl} F_{A/B}&=&k\dfrac{q_{A}\times q_{B}}{AB^{2}}\\&=&k\dfrac{q_{A}\times q_{B}}{\left(2R\sin\alpha\right)^{2}}\\&=&9\cdot10^{9}\dfrac{2\cdot10^{-7}\times 2\cdot10^{-7}} {\left(2\times6\cdot10^{-2}\sin 30^{\circ}\right)^{2}}\\\Rightarrow\;F_{A/B}&=&0.10N \end{array}$
2.1 Représentation, au point $O$, des vecteurs champ électrostatiques de
de $\overrightarrow{E}_{A}$ et $\overrightarrow{E}_{B}$ ( Voir figure) Calcul de la valeur de $\overrightarrow{E}_{A}$
$\begin{array}{rcl} E_{A}&=&k\dfrac{q_{A}}{AO^{2}}\\&=&k\dfrac{q_{A}}{R^{2}}\\&=&9\cdot10^{9}\dfrac{2\cdot^{-7}}{\left(6\cdot10^{-2}\right)^{2}}\\\Rightarrow\;E_{A}&=&5.0\cdot10^{5}N\cdot C^{-1} \end{array}$
2.2 Détermination des caractéristiques du vecteur champ électrostatique $\overrightarrow{E}_{0}=\overrightarrow{E}_{A}+\overrightarrow{E}_{B}$
$-\ $Point, direction et sens : voir figure
$-\ $Intensité :
$\begin{array}{rcl} \dfrac{E_{0 }}{2}&=&E_{A}\\\Rightarrow\;E_{o}&=&2E_{A}\\&=&2\times5.0\cdot10^{5}\\\Rightarrow\;E_{o}&=&10\cdot10^{5}N\cdot C^{-1} \end{array}$
3.1 Représentation de la force $\overrightarrow{F}$ exercée par $q_{A}$ et $q_{B}$ sur la charge $Q_{o}$ (Voir figure)
$Q_{o}$ est signe positif, car la force électrostatique $\overrightarrow{F}=Q_{0}\overrightarrow{E}_{o}$ doit être de même sens que le champ $\overrightarrow{E}_{o}$ pour que le corps ponctuel $(C)$ soit en équilibre
3.2 Écrivons la condition d'équilibre du corps ponctuel $(C)$
Calcul de la masse $m$ du corps
$\begin{array}{rcl} \overrightarrow{P}+\overrightarrow{F}&=&\overrightarrow{0}\\\Rightarrow\;P-F&=&0\\\Rightarrow\;mg-Q_{0}E_{o}&=&0\\\Rightarrow\;m&=&\dfrac{Q_{0}E_{o}}{g}\\\Rightarrow\dfrac{2\cdot10^{-8}\times10\cdot10^{5}}{10}\\\Rightarrow\;m&=&2\cdot^{-3}kg \end{array}$
Exercice 8
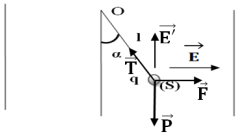
1. Déduction de la valeur de la charge $q.$
La condition d'équilibre, appliquée à la sphère, s'écrit :
$\begin{array}{rcl} \overrightarrow{P}+\overrightarrow{F}+\overrightarrow{T}&=&\overrightarrow{0} \\&\Rightarrow&\left\lbrace\begin{array}{lcl} 0+F-T\sin\alpha&=&0\\ mg+0-T\cos\alpha&=&0 \end{array}\right.\\&\Rightarrow&\left\lbrace\begin{array}{lcl} T\sin\alpha&=&F\quad(1)\\ T\cos\alpha&=&mg\quad(2) \end{array}\right.\\\Rightarrow\tan\alpha&=&\dfrac{qE}{mg}\\\Rightarrow\;q&=&\dfrac{m\times g\times\tan\alpha}{E}\\&=&\dfrac{2\cdot10^{-2}\times10\times\tan 10^{\circ}}{10^{3}}\\\Rightarrow\;q&=&3.5\cdot10^{-5}C \end{array}$
2. Sens et intensité du champ $E'$ pour que le fil s'incline sur la verticale d'un angle
Pour que l'angle soit plus grand, il faut que le champ $\overrightarrow{E'}$ soit dirigé vers le haut (voir figure)
$\begin{array}{rcl} \overrightarrow{P}+\overrightarrow{F}+\overrightarrow{T}&=&\overrightarrow{0}\\&\Rightarrow&\left\lbrace\begin{array}{lcl} 0+qE-T\sin\alpha&=&0\\ mg-qE'+T\cos\alpha&=&0 \end{array}\right.\\&\Rightarrow&\left\lbrace\begin{array}{lcl} T\sin\alpha&=&qE\quad(1)\\ T\cos\alpha&=&qE'-mg\quad(2) \end{array}\right.\\\Rightarrow\tan\alpha&=&\dfrac{qE}{qE'-mg}\\\Rightarrow\;qE'-mg&=&\dfrac{qE}{\tan\alpha}\\\Rightarrow\;E'&=&\dfrac{E}{\tan\alpha}+\dfrac{mg}{q}\\&=&\dfrac{10^{3}}{\tan 20^{\circ}}+\dfrac{2\cdot10^{-2}\times 10}{3.5\cdot10^{-5}}\\\Rightarrow\;E'&=&8.5\cdot10^{3}N\cdot C^{-1} \end{array}$
3. Inclinaison $\alpha'$ si l'on changeait le sens de $E'$ sans modifier,son intensité
$\begin{array}{rcl} M_{\Delta}\left(\overrightarrow{F}\right)+M_{\Delta}\left(\overrightarrow{P}\right)+M_{\Delta}&=&0\\\Rightarrow\;2qEl\cos\alpha+0-C\alpha\\&=&0\\\Rightarrow\;2qEl\cos\alpha\\\Rightarrow\;C\alpha\\\Rightarrow\;q&=&\dfrac{C\alpha}{2El\cos\alpha}\\\Rightarrow\;q&=&\dfrac{13.5\cdot10^{-7}\times\dfrac{pi}{6}}{2\times272\times15\cdot10^{-2}\cos30^{\circ}}\\\Rightarrow\;q&=&4.7\cdot10^{-9}C \end{array}$$\begin{array}{rcl} M_{\Delta}\left(\overrightarrow{F}\right)+M_{\Delta}\left(\overrightarrow{P}\right)+M_{\Delta}&=&0\\\Rightarrow\;2qEl\cos\alpha+0-C\alpha\\&=&0\\\Rightarrow\;2qEl\cos\alpha\\\Rightarrow\;C\alpha\\\Rightarrow\;q&=&\dfrac{C\alpha}{2El\cos\alpha}\\\Rightarrow\;q&=&\dfrac{13.5\cdot10^{-7}\times\dfrac{pi}{6}}{2\times272\times15\cdot10^{-2}\cos30^{\circ}}\\\Rightarrow\;q&=&4.7\cdot10^{-9}C \end{array}$
Exercice 9
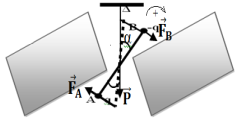
1. Calcul, en fonction de $1$, $\alpha$, $q$ et $E$ le moment des forces électrostatiques par rapport à l'axe de rotation du dispositif.
$\begin{array}{rcl} M_{\Delta}\left(\overrightarrow{F}\right)&=&M_{\Delta}\left(\overrightarrow{F}_{A}\right)+M_{\Delta}\left(\overrightarrow{F}_{B}\right)\\\text{ or }M_{\Delta}\left(\overrightarrow{F}_{A}\right)&=&F_{A}l\cos\alpha\\&=&qEl\cos\alpha\\\text{ et}M_{\Delta}\left(\overrightarrow{F}_{B}\right)&=&F_{B}l\cos\alpha\\&=&qEl\cos\alpha\\\Rightarrow\;M_{\Delta}\left(\overrightarrow{F}\right)&=&3qEl\cos\alpha \end{array}$
2. Calcul du moment du poids du système par rapport à l'axe de rotation.
$\Rightarrow\;M_{\Delta}\left(\overrightarrow{P}\right)=2qE1\cos\alpha$
3. Calcul de $q$
$\begin{array}{rcl} M_{\Delta}\left(\overrightarrow{F}\right)+M_{\Delta}\left(\overrightarrow{P}\right)+M_{\Delta}&=&0\\\Rightarrow\;2qEl\cos\alpha+0-C\alpha&=&0\\\Rightarrow\;2qEl\cos\alpha&=&C\alpha\\\Rightarrow\;q&=&\dfrac{C\alpha}{2El\cos\alpha}\\\Rightarrow\;q&=&\dfrac{13.5\cdot10^{-7} \times\dfrac{\pi}{6}}{2\times272\times15\cdot10^{-2}\cos30^{\circ}}\\\Rightarrow\;q&=&4.7\cdot10^{-9}C \end{array}$
Exercice 10
1. Cas où le point $M$ se trouve sur le segment $[AB]$ entre les points $O$ et $B$ :
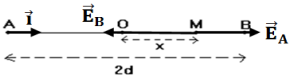
$\begin{array}{rcl} \overrightarrow{E}_{A}&=&-k\dfrac{q}{AM^{2}}\vec{i}\\&=&-k\dfrac{q}{(d+x)^{2}}\vec{i} \end{array}$ ;
$\begin{array}{rcl}\overrightarrow{E}_{B}&=&k\dfrac{q}{BM^{2}}\vec{i}\\&=&k\dfrac{q}{(d-x)^{2}}\vec{i} \end{array}$
$\begin{array}{rcl} \overrightarrow{E}_{M}&=&\overrightarrow{E}_{A}+\overrightarrow{E}_{B}\\&=&-k\dfrac{q}{(d+x)^{2}}\vec{i}+k\dfrac{q}{(d-x)^{2}}\vec{i}\\\Rightarrow\overrightarrow{E}_{M}&=&kq\left(\dfrac{1}{(d-x)^{2}}-\dfrac{1}{(d+x)^{2}}\right)\vec{i}\\\text{En module : }E_{M}&=&kq\left(\dfrac{1}{(d-x)^{2}}-\dfrac{1}{(d+x)^{2}}\right) \end{array}$
2. Cas où le point $M$ se trouve dans l'alignement de $AB$ à l'extérieur du segment $[AB]$ du côté du point $B$

$\begin{array}{rcl} \overrightarrow{E}_{A}&=&\dfrac{q}{AM^{2}}\vec{i}\\&=&k\dfrac{q}{(d+x)^{2}}\vec{i} \end{array}$
$\begin{array}{rcl} \overrightarrow{E}_{B}&=&k\dfrac{q}{BM^{2}}\vec{i}\\&=&k\dfrac{q}{(x-d)^{2}}\vec{i} \end{array}$
$\begin{array}{rcl} \overrightarrow{E}_{M}&=&\overrightarrow{E}_{A}+\overrightarrow{E}_{B}\\&=&k\dfrac{q}{(d+x)^{2}}\vec{i}+k\dfrac{q}{(x-d)^{2}}\vec{i}\\\Rightarrow\overrightarrow{E}_{M}&=&kq\left(\dfrac{1}{(d+x)^{2}+\dfrac{1}{(x-d)^{2}}}\right)\vec{i}\\\text{En module : }E_{M}&=&kq\left(\dfrac{1}{(d+x)^{2}}+\dfrac{1}{(x-d)^{2}}\right) \end{array}$
3. Cas où le point $M$ est situé sur la médiatrice du segment $[AB]$
$\begin{array}{rcl} E_{M}&=&2E_{A}\cos\alpha\\&=&2k\dfrac{q}{AM^{2}}\cos\alpha\text{ avec }AM^{2}\\&=&d^{2}+x^{2}\cos\alpha\\&=&\dfrac{d}{AM}\\&=&\dfrac{d}{\sqrt{d^{2}+x^{2}}}\vec{j} \end{array}$
Exercice 11
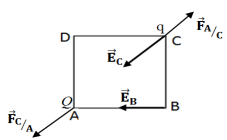
1. Détermination des caractéristiques (valeur,) des champs électriques $\overrightarrow{E}_{B}$ et $\overrightarrow{E}_{C}$ crées par cette charge aux point $B$ et $C.$
$-\ $Point d'application, direction et sens (voir figure)
$-\ $Intensité :
$\begin{array}{rcl} E_{C}&=&E_{B}\\&=&k\dfrac{|Q|}{AC^{2}}\\&=&9.0\cdot10^{9}\dfrac{\left|40\cdot10^{-9}\right|}{\left(\left(2.0\cdot10^{-2}\right)^{2} \left(2.0\cdot10^{-2}\right)^{2}\right)^{2}}\\\Rightarrow\;E_{C}&=&E_{B}\\&=&12.7\cdot10^{3}N\cdot C^{-1} \end{array}$
2. Représentation de ces champs (voir figure)
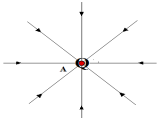
3. Représentation quelques lignes de champs autour du point $A$
4.1 Détermination des caractéristique de la force électrique s'exerçant sur la charge.
$-\ $Point d'application, direction et sens (voir figure)
$-\ $Intensité :
$\begin{array}{rcl} F_{A/C}&=&k\dfrac{|Q||q|}{AC^{2}}\\&=&9.0\cdot10^{9}\dfrac{\left|-40\cdot10^{-9}\right|\left|-10\cdot10^{-9}\right|}{\left(\left(2.0\cdot10^{-2}\right)^{2}+\left(2.0\cdot10^{-2}\right)^{2}\right)^{2}}\\\Rightarrow\;F_{A/C}&=&12.7\cdot10^{-5}N \end{array}$
4.2 Représentation de cette force (voir figure)
4.3 Représentation de la force électrique qui s'exerce sur la charge $Q.$
(Voir figure)

Commentaires
Anonyme (non vérifié)
ven, 12/15/2023 - 20:06
Permalien
Bon document
Mouhamed (non vérifié)
sam, 05/04/2024 - 11:20
Permalien
Nnn
Pendje laure bernice (non vérifié)
lun, 01/06/2025 - 17:02
Permalien
Exercice 8
vandenbulcke maryse (non vérifié)
dim, 05/18/2025 - 15:20
Permalien
erreur
Ajouter un commentaire