Solution des exercices : Énergie et rendement 3e
Classe:
Troisième
Exercice 1
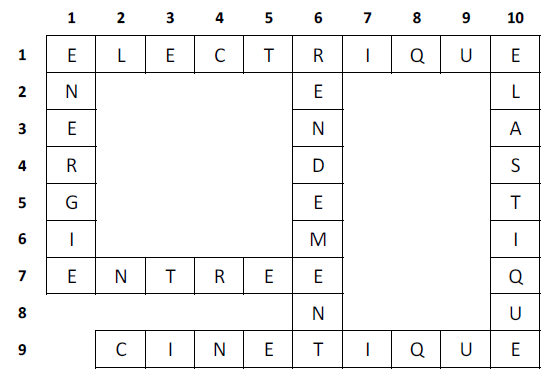
Exercice 2
1) Deux exemples de transformations de l'énergie électrique en énergie calorifique
$-\ $ Cuisinière électrique
$-\ $ Four électrique
2) L'énergie contenue dans un arc tendu est l'énergie élastique. A la lâchée de la flèche, elle se transforme en énergie mécanique.
Exercice 4
Un objet de masse $1\;kg$ est soulevé d'une hauteur de $10\;m$ au bout d'une corde.
1) Calculons le travail mécanique fourni
On a : $W=m\times g\times h$
A.N : $W=1\times 10\times 10=100$
Donc, $$\boxed{W=100\;j}$$
2) Il possède alors de l'énergie mécanique
Exercice 5
Un courant constant d'intensité $I=3\;A$ passe pendant $45\;min$ dans un conducteur de résistance $R=40\;\Omega.$
Calculons la chaleur dégagée par effet joule :
$-\ $ en joules
On a : $E=RI^{2}t$
A.N : $E=40\times 3^{2}\times 45\times 60=972000$
Donc, $$\boxed{E=972000\;j}$$
$-\ $ en calories
On a :
$\begin{array}{rcl} 1\;cal&\longrightarrow&4.18\;j \\ E_{(cal)}&\longrightarrow&972000\;j\end{array}$
Donc, en appliquant la règle de proportionnalité, on obtient :
$\dfrac{E_{(cal)}}{1}=\dfrac{972000}{4.18}\ \Rightarrow\ E_{(cal)}=\dfrac{972000}{4.18}=232535.885$
D'où $$\boxed{E_{(cal)}=232535.885\;cal}$$
Exercice 6
Une centrale électrique nucléaire fournit à un réseau une puissance électrique de $1000\;MW.$
Trouvons le rendement de cette centrale, sachant que la puissance totale du combustible nucléaire fournie à la centrale est de $2800\;MW.$
On a : $r=\dfrac{P_{s}}{P_{e}}$
avec $P_{s}$ la puissance sortante et $P_{e}$ celle entrante
A.N : $r=\dfrac{1000}{2800}=0.357$
Donc, $$\boxed{r=0.357}$$
Exercice 7
Pendant un orage, la foudre qui jaillit entre un nuage et le sol, résulte d'un courant moyen de $10\;kA$ circulant sous une tension de $20\;MV$ pendant $0.1\;s.$
Calculons a puissance et l'énergie électrique mises en jeu
$-\ $ Calcul de la puissance :
On a : $P=UI$
A.N : $P=20\;10^{6}\times 10\;10^{3}=2\;10^{11}$
Donc, $$\boxed{P=2\;10^{11}\;w}$$
$-\ $ Calcul de l'énergie
On a : $E=P\times t$
A.N : $E=2\;10^{11}\times 0.1=2\;10^{10}$
Donc, $$\boxed{E=2\;10^{10}\;j}$$
Exercice 9
Une grue soulève une charge de $600\;N$, d'une hauteur de $30\;cm$ en une minute.
Déterminons le travail effectué
On a : $W=F\times d$
A.N : $W=600\times 30\;10^{-2}=180$
Donc, $$\boxed{W=180\;j}$$
Déterminons la puissance développée
On a : $P=\dfrac{W}{t}$ or $t=1\;mn=60\;s$
A.N : $P=\dfrac{180}{60}=3$
Donc, $$\boxed{P=3\;W}$$
Exercice 10
Un train met $1\;h\;30\;mn\;50\;s$ pour relier 2 villes distantes de $209\;km.$ L'intensité de la force de travail de traction de la locomotive sur les wagons est $F=4.41\;10^{4}\;N.$
1) Calculons la vitesse moyenne de ce train
$-\ $ en $m/s$
On a : $V=\dfrac{d}{t}$
Convertissons la distance $d$ en mètre et le temps $t$ en seconde.
Convertissons la distance $d$ en mètre et le temps $t$ en seconde.
On a : $d=209\;km=209\;10^{3}\;m\ $ et
$\begin{array}{rcl} t&=&1\;h\;30\;mn\;50\;s\\&=&1\times 60\times 60+30\times 60+50\\&=&5450\;s\end{array}$
A.N : $V=\dfrac{209\;10^{3}}{5450}=38.348$
Donc, $$\boxed{V=38.348\;m/s}$$
$-\ $ en $km/h.$
On a : $V=\dfrac{d}{t}$
avec, $d=209\;km\ $ et
$\begin{array}{rcl} t&=&1\;h\;30\;mn\;50\;s\\ \\&=&1+\dfrac{30}{60}+\dfrac{50}{3600}\\ \\&=&1.513889\;h\end{array}$
A.N : $V=\dfrac{209}{1.513889}=138.055$
Donc, $$\boxed{V=138.055\;km/h}$$
2) Calculons le travail mécanique effectué par cette force.
On a : $W=F\times d$
A.N : $W=4.41\;10^{4}\times 209\;10^{3}=92.169\;10^{8}$
Donc, $$\boxed{W=92.169\;10^{8}\;j}$$
3) Calculons la puissance mécanique développée en Chevaux.
On a : $P=\dfrac{W}{t}$
A.N : $P=\dfrac{92.169\;10^{8}}{5450}=1691174.312\;W\ $ or, $\ 1\;kW=1.341\;Ch$
Donc, $P=1691174.312\;10^{-3}\times 1.341=2267.8$
D'où, $$\boxed{P=2267.8\;Ch}$$
Autre méthode
On a : $P=F\times V$
A.N : $P=4.41\;10^{4}\times 38.348=1691146.8\;W$ or $1\;kW=1.341\;Ch$
Donc, $P=1691146.8\;10^{-3}\times 1.341=2267.8$
D'où, $$\boxed{P=2267.8\;Ch}$$
Activités
Sur une ampoule, Momar lit l'information $15W.$
Il souhaite déterminer la tension nominale de la lampe.
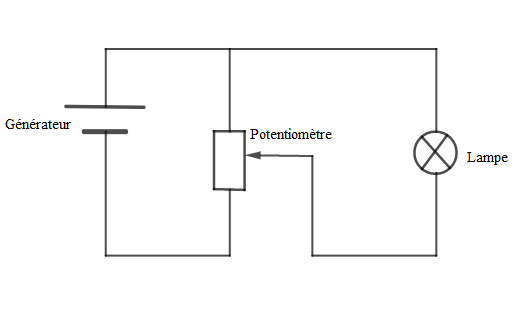
Pour cela, il réalise un montage potentiométrique permettant de mesurer la tension électrique aux bornes de la lampe et l'intensité du courant qui la traverse.
Il obtient les résultats suivants :
$$\begin{array}{|l|c|c|c|} \hline &\text{Mesure }1&\text{Mesure }2&\text{Mesure }3\\ \hline \text{Tension}&6\;V&12\;V&15\;V\\ \hline \text{Intensité}&0.86\;A&1.25A&1.41\;A\\ \hline\text{Puissance électrique reçue}& & &\\ \hline \end{array}$$
1) Réalisons le schéma du montage.

2) a) Pour chaque série de mesures, calculons la puissance reçue par la lampe. Les résultats sont récapitulés dans le tableau ci-dessous :
$$\begin{array}{|l|c|c|c|} \hline &\text{Mesure }1&\text{Mesure }2&\text{Mesure }3\\ \hline \text{Tension}&6\;V&12\;V&15\;V\\ \hline \text{Intensité}&0.86\;A&1.25A&1.41\;A\\ \hline\text{Puissance électrique reçue}&5.16\;W&15\;W&21.15\;W\\ \hline \end{array}$$
D'après le tableau, la tension nominale de la lampe est égale à $12\;V.$
En effet, sur l' ampoule, il est inscrit $15\;W.$ Or, parmi toutes les mesures, seule la mesure 2 donne une puissance électrique égale à cette valeur inscrite. Par conséquent, la mesure 2 donne les valeurs (tension et intensité) nominale de la lampe.
b) La tension appliquée à la lampe lors de la mesure 1 est égale à $6\;V$, elle est donc inférieure à la tension nominale qui est de $12\;V.$
La tension appliquée à la lampe étant à la tension nominale alors, la lampe brillera, mais faiblement.
Exercice 11
Recopions et complétons les phrases suivantes :
L'énergie que possède un corps suspendu à une certaine hauteur du sol est appelée énergie potentielle.
L'énergie cinétique est la forme d'énergie que possède un système en mouvement.
L'énergie mécanique d'un corps est la somme de son énergie potentielle et de son énergie cinétique.
Au cour du mouvement de chute d'un objet, son énergie potentielle est convertie en énergie cinétique.
Un chargeur de portable convertit l'énergie électrique en énergie chimique.
Les photopiles transforment l'énergie lumineux en énergie électrique.
Une pile transforme l'énergie chimique en énergie électrique ; un fer à repasser électrique transforme l'énergie électrique en énergie thermique.
Le rendement d'un moteur est le rapport de l'énergie utile à l'énergie absorbée.
Exercice 12
Un champion de tennis a réalisé un service en communiquant à une balle de masse $m=55\;g$ une vitesse de $217\;km.h^{-1}$
1) Convertissons cette vitesse en $m\cdot s^{-1}$
On sait que : $1\;km=10^{3}\;m\ $ et $\ 1\;h=3600\;s$
Donc,
$\begin{array}{rcl} 217\;km/h&=&\dfrac{217\;km}{1\;h}\\ \\&=&\dfrac{217\cdot10^{3}\;m}{3600\;s} \\ \\&=&\dfrac{217\;m}{3.6\;s}\\ \\&=&\dfrac{60.277\;m}{1\;s}\\ \\&=&60.277\;m.s^{-1}\end{array}$
D'où, $$\boxed{v=60.277\;m.s^{-1}}$$
2) En déduisons l'énergie cinétique fournie à la balle.
L'énergie cinétique fournie à la balle est donnée par la relation :
$$E_{c}=\dfrac{1}{2}\times m\times v^{2}$$
avec, $m=55\;g=55\cdot 10^{-3}\;kg\ $ et $\ v=60.277\;m.s^{-1}$
Ainsi : $E_{c}=\dfrac{1}{2}\times 55\cdot 10^{-3}\times(60.277)^{2}=99.916$
D'où, $$\boxed{E_{c}=99.916\;J}$$
Exercice 13
Une mangue de masse $m=120\;g$ est située sur un arbre à la hauteur $h=3.2\;m$
Déterminons l'énergie potentielle de pesanteur de cette mangue
Soit : $E_{p}=m\times g\times h\ $ avec, $\ m=120\;g=120\cdot 10^{-3}\;kg$
A.N : $E_{p}=120\cdot 10^{-3}\times 9.8\times 3.2=3.76$
Donc, $$\boxed{E_{p}=3.76\;J}$$
Exercice 14
1) Calculons l'énergie cinétique d'un camion, de masse $30$ tonnes, roulant en ville à $30\;km.h^{-1}$ Soit :
$$E_{c}=\dfrac{1}{2}m\times v^{2}$$
Convertissons la masse $m$ en kilogramme et la vitesse en $m.s^{-1}$
On a : $1\text{ tonne}=10^{3}\;kg\ $ donc, $\ m=30\text{ tonne}=30\cdot 10^{3}\;kg$
aussi, $1\;km.h^{-1}=\dfrac{1000\;m}{3600\;s}=0.277\;m.s^{-1}\ $ donc, $\ 30\;km.h^{-1}=30\times 0.277\;m.s^{-1}=8.31\;m.s^{-1}$
avec, $m=30\text{ tonne}=30\cdot 10^{3}\;kg$
Ainsi : $E_{c}=\dfrac{30\cdot 10^{3}\times(8.31)^{2}}{2}=1035841.5$
D'où, $$\boxed{E_{c}=1035841.5\;J}$$
2) Déterminons la vitesse avec laquelle une voiture de masse $1300\;kg$ devrait rouler pour avoir la même énergie cinétique
Comme $E_{c}=\dfrac{1}{2}m\times v^{2}\ $ alors, $m\times v^{2}=2\times E_{c}$
Ce qui donne : $v^{2}=\dfrac{2\times E_{c}}{m}$
Par suite, $v=\sqrt{\dfrac{2\times E_{c}}{m}}$
A.N : $v=\sqrt{\dfrac{2\times 1035841.5}{1300}}=39.92$
D'où, $$\boxed{v=39.92\;m.s^{-1}}$$
Exercice 15
Un conducteur ohmique de résistance $R=100\;\Omega$ est traversé par un courant d'intensité
$I=25\;mA$ pendant une durée $t=5\text{ minutes.}$
1) L'effet Joule est la caractéristique d'un conducteur à dégagé de la chaleur par passage du courant électrique.
2) Calculons la puissance Joule pour ce conducteur ohmique.
Soit : $P=U\times I\ $ or, d'après la loi d'Ohm, $U=R\times I$
Donc, en remplaçant $U$ par $R\times I$, on obtient :
$$P=R\times I^{2}$$
A.N : $P=100\times (25\cdot10^{-3})^{2}=0.0625$
D'où, $$\boxed{P=0.0625\;W}$$
3) Calculons l'énergie dissipée par effet Joule pour ce conducteur ohmique en joules et en $kWh.$
$-\ $ énergie en joule
On a : $E=U\times I\times t\ $ or, $\ U\times I=P$
Donc, $E=P\times t\ $ avec, $\ t=5\;mn=5\times 60\;s=300\;s$
A.N : $E=0.0625\times 300=18.75$
Ainsi, $$\boxed{E=18.75\;J}$$
$-\ $ énergie en $kWh$ :
On a : $1\;kWh=10^{3}\;Wh\ $ et $\ 1\;Wh=3600\;J$
alors,
$\begin{array}{rcl} 1\;kWh&=&10^{3}\;Wh\\ \\&=&3600\;10^{3}\;J\\ \\&=&3.6\;10^{6}\;J\end{array}$
A.N : $E=\dfrac{18.75}{3.6\;10^{6}}=5.208\;10^{-6}$
D'où, $$\boxed{E=5.208\;10^{-6}\;kWh}$$
Exercice 16
Un appartement possède les équipements suivants :
7 lampes de $9\;W$, 4 ventilateurs de $75\;W$, un réfrigérateur de $120\;W$, un téléviseur de $200\;W$ et un fer à repasser de $1.2\;kW$
1) Déterminons la puissance électrique totale de cet appartement si tous les appareils fonctionnent. Soit :
$$P_{\text{Totale}}=P_{\text{lampes}}+P_{\text{ventil}}+P_{\text{réfrig}}+P_{\text{télé}}+P_{\text{fer}}$$
Ainsi,
$\begin{array}{rcl} P_{\text{Totale}}&=&7\times 9+4\times 75+120+200+1.2\;10^{3}\\&=&63+300+120+200+1200\\&=&1883\end{array}$
D'où, $$\boxed{P_{\text{Totale}}=1883\;W}$$
2) Le tableau suivant donne le temps moyen de fonctionnement de chaque appareil.
$$\begin{array}{|l|c|c|c|c|c|}\hline\text{Appareils}&\text{Lampe}&\text{réfrigérateur}&\text{Téléviseur}&\text{Fer à repasser}&\text{Ventilateur}\\ \hline\text{temps}&4\,h&18\,h&8\,h\ 30\,min&15\,min&6\,h\\ \hline\end{array}$$
Calculons, en kilowattheure, l'énergie électrique consommée en $60$ jours.
On sait que l'énergie consommée est donnée par : $E=P\times t$
Calculons l'énergie consommée par chaque appareil en 60 jours :
$-\ $ Lampes
Une lampe fonctionne en moyenne $4\,h$ par jour pour une puissance de $9\;W=9.10^{-3}\;kW$
Donc, l'énergie consommée par les 7 lampes pour une durée de 60 jours est donnée par :
$E_{\text{lampes}}=7\times 9.10^{-3}\times 4\times 60=15.2$
Ainsi, $E_{\text{lampes}}=15.2\;kWh$
$-\ $ Réfrigérateur
Le réfrigérateur, avec une puissance de $120\;W=120.10^{-3}\;kW$, fonctionne en moyenne $18\,h$ par jour.
Donc, pour 60 jours, on a :
$E_{\text{réfrig}}=120.10^{-3}\times 18\times 60=129.6\;kWh$
D'où, $E_{\text{réfrig}}=129.6\;kWh$
$-\ $ Téléviseur
Le téléviseur, avec une puissance de $200\;W=200.10^{-3}\;kW$, fonctionne en moyenne $8\,h\ 30\,mn$ par jour ; soit : $8\,h+\dfrac{1}{2}\,h=8\,h+0.5\,h=8.5\,h$
Par suite, la consommation en 60 jours est donnée par :
$E_{\text{télé}}=200.10^{-3}\times 8.5\times 60=102$
Ainsi, $E_{\text{télé}}=102\;kWh$
$-\ $ Fer à repasser
Le fer à repasser fonctionne en moyenne $15\,mn$ par jour, soit : $\dfrac{1}{4}\,h=0.25\,h$
Donc, $E_{\text{fer}}=1.2\times 0.25\times 60=18$
Ainsi, $E_{\text{fer}}=18\;kWh$
$-\ $ ventilateurs
Un ventilateur, avec une puissance de $75\;W=75.10^{-3}\;kW$, fonctionne en moyenne $6\,h$ par jour.
Donc, l'énergie consommée par les 4 ventilateurs pour une durée de 60 jours est donnée par :
$E_{\text{ventil}}=4\times 75.10^{-3}\times 6\times 60=108$
Ce qui donne, $E_{\text{ventil}}=108\;kWh$
Ainsi, l'énergie électrique totale consommée en $60$ jours est donnée par :
$$E_{\text{Totale}}=E_{\text{lampes}}+E_{\text{réfrig}}+E_{\text{télé}}+E_{\text{fer}}+E_{\text{ventil}}$$
A.N : $E_{\text{Totale}}=15.2+129.6+102+18+108=372.8$
D'où, $$\boxed{E_{\text{Totale}}=372.8\;kWh}$$
3) Calculons le prix à payer pour une consommation bimensuelle.
La consommation bimensuelle est une consommation de deux mois ; soit 60 jours.
Comme la $\text{SENELEC}$ vend en moyenne le $kWh\ $ à $\ 113\text{ F}$ alors, le prix à payer pour une consommation de 60 jours sera donné par :
$$\text{Prix}=113\times E_{\text{Totale}}$$
A.N : $\text{Prix}=113\times 372.8=42126.4$
D'où, $$\boxed{\text{Prix}=42126.4\text{ F}}$$
4) Chaque appareil transforme de l'énergie électrique en d'autres formes d'énergies.
Donnons ces autres formes d'énergies pour la lampe, le fer à repasser et le ventilateur.
$-\ $ Pour la lampe ; l'énergie électrique est transformée en énergie lumineux.
$-\ $ Pour le fer à repasser ; l'énergie électrique est transformée en énergie thermique.
$-\ $ Pour le ventilateur ; l'énergie électrique est transformée en énergie cinétique.

Commentaires
Aziz rayan (non vérifié)
ven, 06/19/2020 - 18:34
Permalien
Formation
Mouhamed pam (non vérifié)
ven, 06/16/2023 - 22:12
Permalien
Exercice 4 est faux l'énergie
Zahra (non vérifié)
dim, 06/23/2024 - 14:25
Permalien
Démentir
Ajouter un commentaire