Série d'exercices : Travail de la force électrostatique-Énergie potentielle électrostatique - 1er s
Classe:
Première
Exercice 1
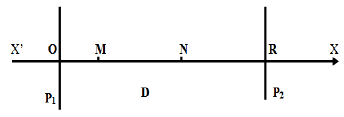
Deux plaques $P_{1}$ et $P_{2}$, planes et parallèles, entre lesquelles règne un vide poussé, sont distantes de $d=10cm$
Elles sont respectivement reliées aux pôles $+$ et $–$ d'un générateur tension qui délivre une tension continue $U=500V$
1. Quels sont, la direction, le sens et l'intensité du champ électrique $\overrightarrow{E}$, supposé uniforme, qui règne dans le domaine situé $D$ entre les deux plaques ?
2. Sur l'axe $XOX'$ perpendiculaire aux plaques, dont l'origine $O$ est sur $P_{1}$ et est orienté de $P_{1}$ vers $P_{2}$, on place les points $M$ et $N$ d'abscisses $X_{M}=2cm$ et $X_{N}=7cm$
Calculer les d.d.p $V_{O}-V_{M}$ ; $V_{O}-V_{N}$ et $V_{M}-V_{N}$
3. Un électron pénètre dans le domaine $D$, au point $R$, avec une vitesse nulle
3.1 Donner les caractéristiques de la force électrostatique $\overrightarrow{F}$ qui s'exerce sur lui
3.2 Quelle est la vitesse de l'électron à son passage en $N$, $M$, puis en $O$
4. Calculer le travail $W(\overrightarrow{F})$ de la force lorsque l'électron déplace de $N$ à $M$
On donne :
$m_{e}=9.1\cdot10^{-31}kg$ ;
charge élémentaire : $e=1.6\cdot10^{-1}$
Exercice 2
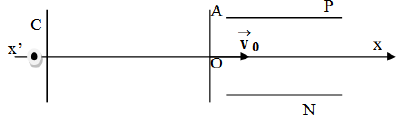
On maintient une $U_{AC}=640V$ entre la cathode $C$ et l'anode $A$ d'un canon à électrons.
La vitesse de sortie des électrons de la cathode est supposée nulle.
La distance $CA=l=5cm$ ; la masse de l'électron $m=9.1\cdot10^{-31}Kg$, la charge élémentaire $e=1.6\cdot10^{-19}C$ ; on néglige le poids de l'électron.
1.1 Déterminer les caractéristiques du vecteur champ électrostatique entre $C$ et $A.$
1.2 Calculer le travail de la force électrostatique appliquée à un électron pour aller de $C$ à $A$
2. Les électrons arrivent au point $O$, avec une vitesse $V=V_{A}$, entre deux plaques conductrices $P$ et $N$ identiques, horizontales, distantes de $d=5cm$ et symétriques par rapport à la direction $xx'.$
Lorsqu'on établit une tension $U_{PN}=1000\,v$, les électrons sortent du champ électrostatique entre $P$ et $N$ en un point $M$ tel que $OM=d'=2\,cm.$
Calculer la tension $U_{OM}.$
3. Calculer l'énergie potentielle électrostatique d'un électron en $O$ puis en $M$, en prenant comme référence la plaque négative $N.$
4. Déterminer le travail de la force électrostatique s'exerçant sur un électron pour aller de $O$ à $M$ en fonction de la variation de l'énergie potentielle électrostatique.
5. Calculer :
5.1 L'énergie cinétique de sortie $E_{CM}$ de l'électron en $M.$
5.2 La vitesse de l'électron $V_{M}$ au point $M.$
Exercice 3
On considère une particule de charge $q$ négative $(q=-2e)$ et de masse $m=3\cdot210^{-27}kg.$
Cette particule, initialement au point $A$ de potentiel $V_{A}=-2.0V$ se dirige vers le point $B$ de potentiel $V_{B}=3.0V.$
Ce déplacement se fait à l'air libre dans un champ électrique uniforme $E$ et à la surface de la Terre, dans le champ de pesanteur uniforme $g.$
1. Faire l'inventaire des forces que subit cette particule au cours de son déplacement de $A$ vers $B.$ (On n'en négligera aucune à cette question).
2. Parmi ces forces, quelles sont celles que l'on qualifie de « conservatives » ?
3. En supposant que la trajectoire de la particule est rectiligne, donner l'expression du travail de la force de frottement de l'air $f$, supposée constante entre $A$ et $B$, en fonction de $AB$ et $f.$
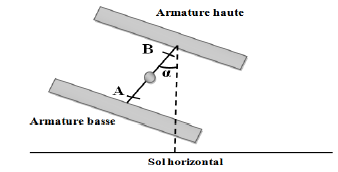
On suppose à présent qu'il règne un vide parfait entre ces deux armatures.
4. Quel est le signe de la charge électrique de l'armature haute ?
Justifier.
5. Représenter, sans tenir compte de leur norme, le champ électrique $E$ et le champ de pesanteur $g$ sur la figure ci-contre.
6. Donner l'expression du travail de la force électrique $F_{e}$, puis du poids $P$, en fonction de $m$, $q$, $V_{A}$, $V_{B}$, $g$, $\alpha$ et $AB.$
7. Préciser pour chacune de ces forces si leur travail est moteur ou résistant.
8. Calculer le travail de ces forces sur le trajet $AB=1.8m$ et conclure que l'on peut négliger l'énergie potentielle de pesanteur de la particule.
Alors, on ne prend en compte que l'énergie potentielle électrique.
On rappelle l'expression de l'énergie potentielle électrique : $E_{Pe}=q\cdot U_{AB}$
9. Déduire de la conclusion précédente l'expression de l'énergie mécanique de la particule au point $A$ en fonction de sa vitesse $v_{A}$ et des grandeurs $V_{A}$, $q$, et $m.$
10. Même question au point $B$ en fonction de la vitesse $v_{B}$ et des grandeurs $V_{B}$, $q$, et $m.$
11. Justifier pourquoi l'énergie mécanique se conserve.
12. En déduire la vitesse $v_{B}$ de la particule sachant que $v_{A}=0.53 m\cdot s^{-1}$
Données :
charge élémentaire $e=1.6\cdot10^{-19}C$ ;
Champ de pesanteur $g=9.8N/kg$ ;
$\alpha=30^{\circ}$ ;
$E=\dfrac{U}{d}$ ;
$U_{AB}=V_{A}-V_{B}$
Exercice 4 : Travail d'une force électrostatique
Deux armatures métalliques $P_{A}$ et $P_{B}$, parallèles entre elles et distantes de $d$, sont reliées aux bornes d'un générateur de tension continue.
Entre ces deux armatures règne un champ électrostatique $\overrightarrow{E}$ uniforme.
1. Donner l'expression du travail de la force électrostatique $\overrightarrow{E}$ qui s'exerce sur une particule de charge $q$ se déplaçant d'un point $A$ de l'armature $P_{A}$ à un point $B$ de l'armature $P_{B}.$
L'exprimer en fonction de $E$, $AB$ et $q.$
2. Montrer que le travail de cette force s'écrit : $W_{AB}(\overrightarrow{F})=q\cdot U_{AB}.$
3. Calculer sa valeur dans le cas d'un noyau d'hélium $He^{2+}$ se déplaçant de $A$ à $B.$
Données :
$e=1.60\times 10^{-19}C$ ; $U_{AB}=400\,V$
Exercice 5
Une particule $\alpha$ (noyau d'hélium), produite par une source radioactive, est émise au voisinage d'un point $A.$
La valeur de sa vitesse en $A$ est négligeable devant celle qu'elle peut atteindre en $B.$
Entre les points $A$ et $B$ règne un champ électrostatique uniforme qui permet l'accélération de la particule.
Le poids et les frottements sont négligeables lors de ce mouvement.
1. Quelle est la charge $q_{\alpha}$ de la particule $\alpha$ ?
2. Établir l'expression du travail de la force électrostatique s'appliquant sur la particule $\alpha$ se déplaçant entre $A$ et $B.$
Exprimer ce travail en fonction $q\alpha$, $V_{A}$ et $V_{B}.$
$(V_{A}$ et $V_{B}$ sont les potentiels respectifs aux points $A$ et $B.)$
3. En déduire l'expression de la variation d'énergie potentielle électrique entre $A$ et $B.$
4. L'énergie mécanique se conserve-elle ?
Justifier.
5.1 À partir des réponses précédentes, exprimer la différence de potentiel $V_{A}-V_{B}$ en fonction de $v_{B}$, $m_{\alpha}$ et $q_{\alpha}$
5.2 Calculer cette valeur sachant que la vitesse en $B$ a pour valeur $v_{B}=1.00\cdot10^{3}km\cdot s^{-1}.$
Données :
$e=1.60\cdot10^{-19}C$ ; $m_{\alpha}=6.70\times 10^{-27}kg.$
Exercice 6
Au voisinage de la Terre, près du sol, il existe un champ électrostatique uniforme, vertical et dirigé vers le sol.
Sa norme varie linéairement avec l'altitude selon la loi $E=a+bz$ entre les altitudes $z=0$ et $z=1\ 400m.$
1) Sachant que pour $z=0$, $E=100V\cdot m^{-1}$ et que pour $z=1\ 400m$, $E=20V\cdot m^{-1}$, déterminer les constantes $a$ et $b.$
Quelles sont leurs unités ?
Représenter graphiquement $E$ en fonction de $z.$
2) Par une méthode graphique, déterminer le travail des forces électriques s'exerçant sur une charge de $10^{-10}C$ se déplaçant de l'altitude $O$ à l'altitude $z.$
En déduire le potentiel électrostatique d'un point situé à l'altitude $h$ si l'on prend comme référence la surface terrestre.
3) Un ion $H^{+}$ est formé à l'altitude $z=1\ 400m.$
Le champ de pesanteur est supposé uniforme, d'intensité $g=10m\cdot s^{-2}.$
Calculer l'énergie potentielle de pesanteur et l'énergie potentielle électrostatique de cet ion.
Les comparer.
Si l'ion part de l'altitude $z=1400m$ avec une vitesse nulle, quelle sera sa vitesse à l'arrivée sur le sol (on négligera toutes les autres interactions) ?
Exercice 7
La sphère, supposée petite et chargée positivement, d'un pendule électrostatique est en équilibre en un point $O$ situé entre deux plaques $P$ et $N$ conductrices, parallèles et distantes de $d=15cm.$
Les plaques sont initialement neutres.
On applique une tension $U_{PN}=1\ 500V$ entre les deux plaques.
La sphère chargée adopte, après quelques oscillations, une nouvelle position d'équilibre $A.$
1) Calculer la charge $q$ du pendule si, à l'équilibre, l'angle $\alpha$ que fait le fil de suspension avec la verticale vaut $30^{\circ}$ ; la sphère est attirée du côté de la plaque négative $N.$
2) Le point $O$ est pris comme point de référence $\alpha$ est l'angle que fait le fil du pendule avec la verticale lorsque la sphère est attirée par la plaque $N.$
Pour $\alpha\in\left[0\;,\ \dfrac{\pi}{2}\right[$, exprimer en fonction de $\alpha$ l'énergie potentielle de pesanteur $\mathcal{E}_{pg}$ et l'énergie potentielle électrostatique $\mathcal{E}_{pe}.$
Représenter graphiquement $\mathcal{E}_{pg}$ et $\mathcal{E}_{pe}$ en fonction de $\alpha.$
En déduire la représentation graphique de la somme $\mathcal{E}_{p}$ de ces énergies potentielles.
Pour quelle valeur de $\alpha$ cette somme est-elle minimale ?
Conclure.
Données :
masse de la sphère : $m=0.5g$ ;
longueur du fil : $l=20m$ ; $g=10m\cdot s^{-2}$
Exercice 8
Un générateur maintient une tension $U=200V$ entre deux plaques conductrices parallèles situées dans le vide.
1) Un électron quitte la plaque négative pour être capté par la plaque positive.
Calculer le travail de la force électrostatique qui s'exerce sur cet électron (en joules et en électronvolts).
2) La distance séparant les plaques est $d=2cm.$
Caractériser le champ électrostatique en tout point de l'espace compris entre les plaques.
3) On écarte les plaques, toujours parallèles, à $d'=4cm$ ; la tension de $200V$ est maintenue.
Reprendre les questions précédentes.
Conclure.
4) Les plaques sont déplacées de façon quelconque et ne sont plus parallèles.
Peut-on toujours calculer simplement le travail de la force électrostatique qui s'exerce sur l'électron allant de la plaque positive à la plaque négative ?
Exercice 9
Une d.d.p $V_{1}-V_{2}=100V$ est appliquée entre deux grilles métalliques planes, parallèles, $G_{1}$ et $G_{2}.$
Entre ces deux grilles règne un champ électrostatique uniforme ; il est nul en dehors de cette zone.
Des électrons, émis par un canon à électrons suivant les lignes de champ, traversent la grille $G_{1}$ avec la vitesse $V_{1}.$
1) Quelle est la vitesse $V_{1}$ minimale des électrons qui parviennent à traverser la grille $G_{2}$ ?
2) Quelle est la vitesse $V_{2}$ d'un électron traversant $G_{2}$ après avoir traversé $G_{1}$ avec la vitesse $V_{1}=9\cdot10^{6}m\cdot s^{-1}$ ?
3) Dans les conditions de la deuxième question, un électron rencontre un neutron immobile se trouvant au voisinage de $G_{2}.$
Le choc est élastique, et l'électron repart avec une vitesse de sens opposé .
Avec quelle vitesse retraverse-t-il $G_{1}$ ?
On fera les approximations légitimes.
Données :
$m_{e}=9.1\cdot10^{-31}kg$ ; $m_{n}=1\ 840m_{e}.$
On indique qu'au cours d'un choc élastique il y a conservation de l'énergie cinétique et conservation de la quantité de mouvement du système (électrons, neutron).
Exercice 10
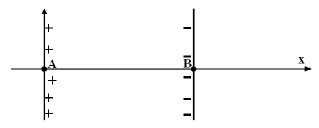
Deux plaques métalliques verticales parallèles $A$ et $B$ séparées d'une distance $d=3.45cm$ sont portées aux potentiels $V_{A}=-500V$ et $V_{B}=+500V.$
Ces deux plaques forment un condensateur plan.
On rappelle que la tension $U_{AB}=V_{A}-V_{B}$, et on donnera un nombre correct de chiffres significatifs
1. Donner les caractéristiques (sens, direction et valeur) du champ électrique entre les armatures du condensateur et dessiner quelques lignes de champs
2. On insère entre les $2$ plaques un fil de masse négligeable auquel est accrochée une petite boule de masse $m=2.5g.$
Initialement la boule ne porte pas de charges électriques et le pendule ainsi formé est vertical.
On apporte ensuite à la boule une charge $q=-0.50\mu C.$
Le pendule s'incline alors d'un angle $\alpha30^{\circ}$ vers la droite par rapport à la position précédente.
2.1 Sur une autre figure, dessiner le pendule incliné en équilibre ainsi que les forces exercées sur la boule.
2.2 Calculer l'intensité du champ électrique pour que le fil s'incline d'un angle $\alpha=30^{\circ}$ vers la droite par rapport à la verticale.
On prendra $g=10m\cdot s^{-2}$
2.3 De quel angle le fil s'incline-t-il par rapport à la verticale Si le champ a une valeur de $1.0\cdot10^{4}V\cdot m^{-1}$ ?
On prendra $g=10 m\cdot s^{-2}.$

Commentaires
Khady Sall (non vérifié)
dim, 09/27/2020 - 12:39
Permalien
Je suis satisfait par les
Omar Barry (non vérifié)
ven, 12/18/2020 - 22:08
Permalien
Devenir un grand scientifique
Kadia (non vérifié)
mer, 06/09/2021 - 23:30
Permalien
Être un bon scientifique
Papa Oumar Niang (non vérifié)
jeu, 04/08/2021 - 14:41
Permalien
Bonjour je suis heureux de
Slm je veux le ... (non vérifié)
dim, 05/02/2021 - 02:09
Permalien
Exo 1
Khoudia (non vérifié)
dim, 06/06/2021 - 23:19
Permalien
La correction exo1
Hajar (non vérifié)
lun, 03/24/2025 - 00:59
Permalien
Travail
koffi konan yacinthe (non vérifié)
mar, 03/08/2022 - 12:52
Permalien
demande de correction
Slm je veux le ... (non vérifié)
dim, 05/02/2021 - 02:09
Permalien
Exo 1
Abdoulaye camara (non vérifié)
lun, 06/14/2021 - 17:21
Permalien
Ces sont des meilleurs
Ingrid (non vérifié)
mer, 02/19/2025 - 22:23
Permalien
Demande de la correction de l’exercice 1
Nissrine Elmniai (non vérifié)
dim, 05/23/2021 - 10:56
Permalien
Je veux ces exercices
Diakaria camara (non vérifié)
mar, 06/15/2021 - 03:46
Permalien
Merci
Siby (non vérifié)
dim, 07/04/2021 - 19:05
Permalien
Exo8
Royal (non vérifié)
lun, 07/05/2021 - 23:50
Permalien
Quelle objet
Martine Agathe (non vérifié)
mar, 07/06/2021 - 02:16
Permalien
Être bien en PC
Dija (non vérifié)
sam, 07/10/2021 - 13:33
Permalien
Correction
Anonyme (non vérifié)
ven, 06/10/2022 - 02:43
Permalien
Correction exo 10
Anonyme (non vérifié)
ven, 06/10/2022 - 02:43
Permalien
Correction exo 10
Birame ngom (non vérifié)
jeu, 06/16/2022 - 20:12
Permalien
Participation
Ajouter un commentaire