Série d'exercices : Réactions nucléaires - Ts
Classe:
Terminale
Exercice 1
Données :
Unité de masse atomique : $u=1.660 54\times 10^{-27}kg$
Énergie de masse de l'unité de masse atomique : $E=931.5MeV$, $c=3.0\cdot10^{8}m\cdot s^{-1}.$
$$\begin{array}{|c|c|c|c|c|c|c|} \hline \text{Nom du noyau}&\text{Radon}&\text{Radium}&\text{Hélium}&\text{Neutron}&\text{Proton}&\text{Électron}\\ \text{ou de la particule}& & & & & &\\ \hline \text{Symbole}&_{86}^{222}Rn&_{88}^{226}Ra&_{2}^{4}He&_{0}^{1}n&_{1}^{1}p&_{-1}^{0}e\\ \hline \text{Masse (en u)}&221.970&225.977&4.001&1.009&1.007&5.49\times10^{-4}\\ \hline \end{array}$$
1. Désintégration du radium
L'air contient du radon $222$ en quantité plus ou moins importante.
Ce gaz radioactif naturel est issu des roches contenant de l'uranium et du radium.
Le radon se forme par désintégration du radium $($lui-même issu de la famille radioactive de l'uranium $238)$, selon l'équation de réaction nucléaire suivante :
$_{88}^{226}Ra\ \rightarrow\ _{86}^{222}Rn\ +\ _{2}^{4}He$
1.1 Quel est le type de radioactivité correspondant à cette réaction de désintégration ?
Justifier votre réponse.
1.2 Défaut de masse
Donner l'expression littérale du défaut de masse $\Delta\,m$ du noyau de symbole $_{Z}^{A}X$ et de masse $m_{X}$
Calculer le défaut de masse du noyau de radium $Ra.$
L'exprimer en unité de masse atomique $u.$
1.3 Écrire la relation d'équivalence masse-énergie.
1.4 Le défaut de masse $\Delta\,m$ $(Rn)$ du noyau de radon $Rn$ vaut $3.04\times 10^{-27}\,kg$
Définir l'énergie de liaison $E_{1}$ d'un noyau.
Calculer, en joule, l'énergie de liaison $E_{1}(Rn)$ du noyau de radon.
Vérifier que cette énergie de liaison vaut $1.71\times10^{3}MeV.$
En déduire l'énergie de liaison par nucléon $\dfrac{E_{1}}{A}$ du noyau de radon.
Exprimer ce résultat en $MeV\cdot nucléon^{-1}.$
1.5 Bilan énergétique
Établir littéralement la variation d'énergie $\Delta\,E$ de la réaction $(1)$ en fonction de $m_{Ra}$, $m_{Rn}$ et $m_{He}$ masses respectives des noyaux de radium, de radon et d'hélium.
Exprimer $\Delta\,E$ en joule $m_{X}.$
Exercice 2 Radioactivité et médecine
La médecine désigne l'ensemble des applications ou des substances radioactivités sont associées au diagnostic et à la thérapie.
Depuis des années $1930$, la médecine nucléaire progresse grâces à la découverte et à la maîtrise de nouveaux isotopes.
La radiothérapie vise à administrer un radio pharmaceutique dont les rayonnements ionisants sont destinés à traiter un organe cible dans un but curatif ou palliatif.
Ainsi on utilise du rhénium $186$ dans le but de soulager la maladie rhumatoïde et du phosphore $32$ pour réduire la production excessive de globules rouges dans la moelle osseuse.
La première partie de cet exercice traite de l'utilisation du rhénium $186$ et la seconde partie de l'utilisation du phosphate $32.$
On s'intéresse à l'aspect physique des phénomènes, les aspects biologique ne sont pas pris en compte.
Données :
$-\ $ temps de demi-vie du rhénium $186$ : $t_{1/2}\left(_{Z}^{186}Re\right)=3.7\,j$ (jours) ;
$-\ $ masse molaire du rhénium $186$ : $M\left(_{Z}^{186}Re\right)=186\,g\cdot mol^{-1}$ ;
$-\ $ constantes radioactives : $\lambda\left(_{Z}^{186}Re\right)=2.2\cdot10^{-6}\,s^{-1}$ ;
$\lambda\left(_{15}^{32}P\right)=5.6\cdot10^{-7}\,s^{-1}$ ;
$-\ $ masse de quelque noyaux et particules : $m\left(_{15}^{32}P\right)=5.30803\cdot10^{-26}\,kg$ ;
$m\left(_{16}^{32}S\right)=5.30763\cdot10^{-26}\,kg$ ;
$m\left(_{-1}^{0}e\right)=9.1\cdot10^{-31}\,kg$ ;
$-\ $ célérité de la lumière dans le vide : $c=3.0\cdot10^{8}\,m\cdot s^{-1}$ ;
$-\ $ constante d'Avogadro : $N_{A}=6.0\cdot10^{23}\,mol^{-1}$
$-\ $ électron-volt : $1eV=1.6\cdot10^{-19}\,j.$
1) Injectionnintra-articulaire d'une solution
contenant du rhénium $186$
1.1 Le rhénium $186$ $(\ )$ est un noyau radio actif $\beta^{-}.$
Sur le diagramme $(N\;,\ Z)$ de la figure 3 ci-dessous ou $N$ représente le nombre de neutrons et $Z$ le nombre de protons, la courbe tracée permet de situer la vallée de stabilité des isotopes.
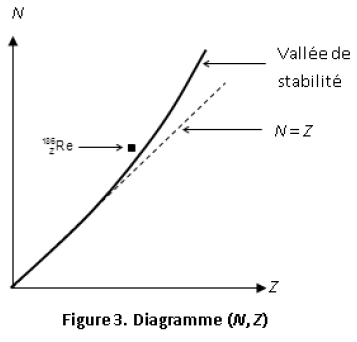
Le point représentatif du noyau de rhénium $186$ est placé au-dessus de cette courbe.
1.1.1 Déduire de ce diagramme si cet isotope radio actif possède un excès de neutron(s) ou un excès de proton(s) par rapport à un isotope stable du même élément.
1.1.2 Quel nom porte la particule émise au cours d'une désintégration
1.2.3 Écrire l'équation de la désintégration du noyau de rhénium $186$ noté $\left(_{Z}^{186}Re\right)$ sachant que le noyau fils obtenu correspond à un isotope de l'osmium noté $\left(_{76}^{A}Os\right).$
En énonçant les lois utilisées, déterminer les valeurs de $A$ et de $Z.$
On admet que le noyau fils obtenu lors de cette transformation n'est pas dans un étant excité.
2. Injection intraveineuse d'une solution contenant du phosphore $32$
Carte d'identité du phosphore $32$ (tableau)
$$\begin{array}{|c|c|} \hline \text{nom de l'isotope}&\text{Phosphore }32\\ \hline \text{symbole}&_{15}^{32}P\\ \hline \text{type de radioactivité}&\beta^{-}\\ \hline \text{énergie du rayonnement}&1.7\,MeV\\ \text{émis}&\\ \hline \text{équation de la}&_{15}^{32}P\ \rightarrow\ _{16}^{32}S\ +\ _{-1}^{0}e\\ \text{désintégration}&\\ \hline \text{demi-vie}&14\text{ jours}\\ \hline \end{array}$$
l'injection en voie veineuse d'une solution contenant du phosphore $32$ radio actif permet dans certains cas de traiter une production excessive de globules rouges au niveau des cellules de la moelle osseuses.
2.1 Donner la composition du noyau de phosphore $32.$
2.2 A l'aide des masse données en début d'exercice et de la carte d'identité du phosphore $32$, vérifier par un calcule la valeur $E$ de l'énergie du rayonnement émis par la désintégration du phosphore $32.$ $Non\ faisable\ pour\ l'instant\;!$
2.3 Pour la très grande majorité d'entre eux, les noyaux fils obtenus de cette transformation ne sont pas dans un état excité.
A quel type de rayonnement particulièrement pénétrant le patient n'est-il pas exposé ?
2.4 Rappeler la loi de décroissance du nombre $N(t)$ de noyaux radioactifs d'un échantillon en fonction de $\lambda$ et $N_{0}$ $($nombre de noyaux radio actifs à la date $t=0.)$
2.5 Définir le temps le temps de demi-vie radioactive $t_{1/2}$ et établir la relation qui existe entre la demi-vie et la constante de désintégration radio active $\lambda.$
2.6 Vérifier, par un calcul, la valeur approchée du temps de demi-vie proposée dans la carte d'identité ci-dessus.
Exercice 3
1. Temps de demi-vie
Le thorium $^{230}Th$ est utilisé dans la datation des coraux et concrétions carbonatées ainsi que dans la datation des sédiments marins et lacustres.
Dans un échantillon de $«$ thorium $230\ »$, on appelle $N(t)$ le nombre de noyaux de thorium présents à chaque date $t$ et $N_{0}$ celui des noyaux présents à la date $t_{0}=0\;an.$
On a représenté ci-dessous la courbe donnant le rapport $\dfrac{N(t)}{N_{0}}$
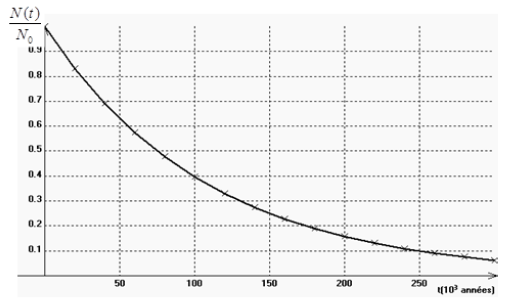
1.1 Le noyau $^{230}Th$ est un émetteur $\alpha$ et se désintègre pour donner du $_{88}Ra.$
Indiquer ce que représente $\alpha$ et écrire l'équation de la réaction nucléaire correspondante, en précisant les lois utilisées (le noyau de radium est obtenu dans un état non excité)
1.2 Donner la définition du temps de demi-vie $$t_{1/2}.$
Vérifier que sa valeur est de $7.5\times10^{4}$ années en expliquant succinctement la méthode utilisée.
1.3 Donner l'expression mathématique de la loi de décroissance radioactive et calculer la constante radioactive en année$^{-}.$
1.4 Parmi ces grandeurs :
l'âge de l'échantillon de noyaux la quantité initiale de noyaux.
La température la nature des noyaux
Quelle est la seule grandeur qui fait varier le temps de demi-vie ?
1.5 Le thorium $^{230}Th$ fait partie de la famille radioactive de l'uranium $^{238}U.$
Une famille radioactive est composée d'un ensemble de noyaux radioactifs, tous issus d'un noyau initial instable qui, de père en fils, par désintégrations successives conduisent à un noyau stable, ici le $«$ plomb $206\ ».$
L' $«$ uranium $238\ »$, dissous à l'état de traces dans l'eau de mer, produit des atomes de $«$ thorium $230»$ suivant les réactions nucléaires suivantes :
$$_{92}^{238}U\ \rightarrow\ _{90}^{234}Th\ \rightarrow\ _{91}^{234}Pa\ \rightarrow\ _{Z_{4}}^{234}U\ \rightarrow\ _{Z_{5}}^{230}Th$$
Donner les valeurs de $Z_{4}$ et $Z_{5}$, en les justifiant, et indiquer le type de radioactivité pour les deux premières transformations.
1.6 Au début de leur formation, les concrétions carbonatées des coraux contiennent de l' $«$ uranium $238\ »$ et pas de $«$ thorium $230\ ».$
La méthode de datation de ces carbonates repose sur le rapport des nombres de noyaux : $N^{230}Th/N^{238}U.$
Ce rapport augmente au cours du temps jusqu'à $«$ l'équilibre séculaire $».$
Celui-ci correspond à l'état où les deux populations des noyaux d' $«$ uranium $238\ »$ et de $«$ thorium $230\ »$ ont même activité.
1.6.1 L'activité $A(t)$ d'une population de noyaux identiques est définie ici par :
$$A(t)=-\dfrac{\mathrm{d}N(t)}{\mathrm{d}t}$$
En vous aidant de la question 1.3
Démontrer que $A(t)=\lambda\cdot N(t)$ pour une population de noyaux donnée.
1.6.2 En déduire, qu'à l'équilibre séculaire, le rapport $N^{230}Th/N^{238}U$ est constant
Exercice 4
A. Le plutonium $_{94}^{241}Pu$ est radioactif $\beta^{-}$, il donne l'américium $_{Z}^{A}Am.$
1) Écrire l'équation de la réaction nucléaire correspondante.
Préciser les lois utilisées.
2) Déterminer la composition de chacun des deux noyaux $(Pu$ et $Am).$
Déduire l'origine de la particule émise $(\beta^{-}).$
B. le noyau $_{Z}^{A}Am$ d'américium est radioactif $\alpha.$
Il se désintègre en donnant un noyau de neptunium $(Np)$ dans son état fondamental.
1) Écrire l'équation de cette désintégration.
2) Montrer que cette réaction libère une énergie $W.$
Calculer $($en $Mev)$ l'énergie $W$ libérée par la désintégration d'un noyau d'américium.
On donne :
$m_{\alpha}=4.0015\,u$,
$m_{Am}=241.0567\,u$,
$m_{Np}=237.0480\,u$,
$1\,u=931.5,Mev\cdot c^{-2}$
3) Le noyau $_{94}^{241}Am$ est supposé au repos.
D'après les lois de conservation on montre que :
$m_{\alpha}\cdot E_{C\alpha}=m_{Np}\cdot E_{C_{Np}}$
On admet que l'énergie $W$ libérée par cette désintégration est communiquée totalement aux particules formées sous forme d'énergie cinétique.
$W=E_{C\alpha}+E_{C_{Np}}$
Calculer $($en $Mev)$ $E_{C\alpha}$ et $E_{C_{Np}}.$
4) A une date $t_{0}=0s$, on dispose d'un échantillon contenant $N_{0}$ noyaux d'américium $_{95}^{241}Am.$
A différents dates $t$, on mesure, à l'aide d'un compteur de Geiger, son activité A.
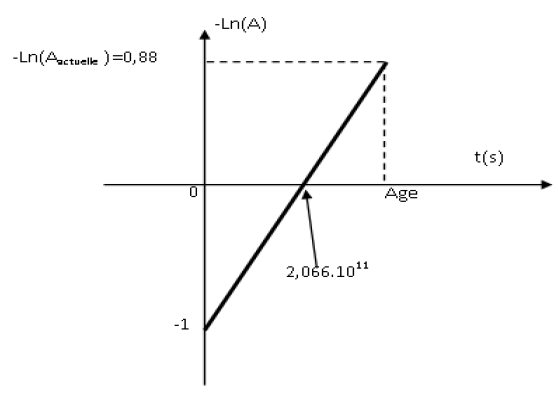
On obtient la courbe représentée ci-dessous : $-Ln(A)=f(t)$
a) Définir l'activité d'une substance radioactive, donner son unité.
En utilisant la loi de décroissance radioactive : $N=N_{0}\cdot e^{-\lambda\,t}$,
Montrer que $-Ln(A)=\lambda\,t=–Ln(A_{0}).$
b) Déterminer graphiquement :
$-\ $ La valeur de la constante radioactive $\lambda$ de $_{95}^{241}Am.$
Déduire sa période $T.$
$-\ $ L'activité $A_{0}$ de l'échantillon d'américium $_{95}^{241}Am.$
Déduire $N_{0}.$
$-\ $ L'activité actuelle.
Calculer l'âge de l'échantillon d'américium.
Exercice 5 : L'age de la terre
La détermination de l'âge de la Terre a commencé vers le $XVI^{ième}$ siècle, on
l'estimait alors autour de $5\ 000$ ans.
Au $XIX^{ième}$ siècle, des scientifiques admettaient un âge d'environ $100$ millions d'années.
La découverte de la radioactivité, par $H.$
Becquerel en $1896$, bouleversa toutes les données connues.
La datation à l'uranium-plomb permit de déterminer assez précisément l'âge de la Terre.
Nous proposons de comprendre cette technique de datation.
I. Étude de la famille uranium $238$ $–$ plomb $206$
Le noyau d'uranium $238$, naturellement radioactif, se transforme en un noyau de plomb $206$, stable, par une série de désintégrations successives.
Nous allons étudier ce processus.
$($On ne tiendra pas compte de l'émission $\gamma).$
1) Dans la première étape, un noyau d'uranium $_{92}^{238}U$ subit une radioactivité $\alpha.$
Le noyau fils est du thorium $($symbole $Th).$
a) Qu'est-ce qu'un noyau radioactif ?
b) Écrire l'équation de la réaction nucléaire en précisant les règles utilisées.
c) Calculer l'énergie libérée au cours de cette désintégration en joule puis en $Mev.$
On donne :
$$\begin{array}{|c|c|c|c|} \hline \text{Symbole du noyau}&_{92}^{238}U&_{2}^{4}He&_{Z}^{A}Th\\ \hline \text{Masse du noyau (en u)}&238.0508&4.0015&234.0436\\ \hline \end{array}$$
$1\,u=1.66\cdot10^{-27}Kg$ et $1\,ev=1.6\cdot10^{-19}J.$
2) Dans la deuxième étape, le noyau de thorium $234$ se transforme en un noyau de protactinium $_{91}^{234}Pa.$
L'équation de la réaction nucléaire est : $_{90}^{234}Th\ \rightarrow\ _{91}^{234}Pa\ +\ _{-1}^{0}e$
a) Donner le type de radioactivité correspondant à cette transformation et préciser son origine.
b) L'équation globale du processus de transformation d'un noyau d'uranium $238$ en un noyau de plomb $206$ est : $_{92}^{238}U\ \rightarrow\ _{82}^{206}Pb\ +\ x\;_{-1}^{0}e\ +\ y\;_{2}^{4}He$
Déterminer, en justifiant, le nombre de désintégrations $\alpha$ et $\beta^{-}$ de ce processus.
II. Géochronologie :
On a constaté d'une part, que les minéraux d'une même couche géologique, donc du même âge, contiennent de l'uranium $238$ et du plomb $206$ en proportions remarquablement constantes, et d'autre part que la quantité de plomb dans un minéral augmente proportionnellement à son âge relatif.
Si on mesure la quantité de plomb $206$ dans un échantillon de roche ancienne, en considérant qu'il n'y en avait pas initialement, on peut déterminer l'âge du minéral à partir de la courbe de décroissance radioactive du nombre de noyaux d'uranium $238.$
Étudions un échantillon de roche ancienne dont l'âge, noté terre, correspond à celui de la Terre.
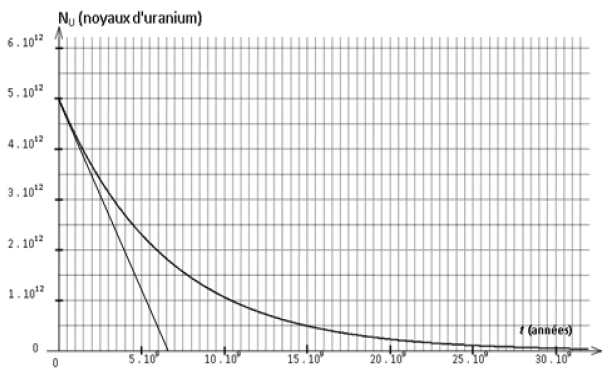
1) On considère la courbe de décroissance radioactive du nombre $N_{U}(t)$ de noyaux d'uranium $238$ dans un échantillon de roche ancienne. (figure 1).
Sachant que $\mathrm{d}N_{U}$ est le nombre de noyaux qui se désintègrent pendant l'intervalle de temps $\mathrm{d}t.$
a) Prélever à partir du graphe, la quantité initiale $N_{U}(0)$ de noyaux d'uranium.
b) Montrer que $N_{U}(t)$ vérifie l'équation différentielle $\dfrac{\mathrm{d}N_{U}}{\mathrm{d}t}+\lambda\,N_{U}=0$ avec $\lambda$ est la constante radioactive de l'uranium $238.$
c) Sachant que la solution de l'équation différentielle précédente s'écrit sous la forme $N_{U}(t)=B\cdot e^{-t/\tau}$, montrer que $B=N_{U}(0)$ et que $\lambda=\dfrac{1}{\tau}$
d) Déterminer à partir du graphe la constante de temps $\tau$ de l'uranium $238.$
e) Définir la demie-vie $T$ et établir une relation entre $T$ et $\tau.$
Calculer $T.$
Retrouver la valeur de $T$ graphiquement.
2) La détermination du nombre de noyaux d'uranium $238$ est effectuée à l'aide d'un compteur de Geiger Müller qui mesure l'activité d'un échantillon d'une substance radioactive.
a) Définir l'activité radioactive.
Calculer, en becquerel, l'activité initiale de l'uranium $238.$
$($une année$=365.25\cdot24.3600\,s=3.15\cdot10^{7}s.)$
b) Déterminer graphiquement et par calcul l'activité de l'uranium à $t=15\cdot10^{9}$ années.
3) La quantité de plomb mesurée dans la roche à la date $t_{Terre}$, notée $N_{Pb}(t_{Terre})$, est égale à $2.5\cdot10^{12}$ atomes.
a) Établir la relation entre $N_{U}(t_{Terre})$, $N_{U}(0)$ et $N_{Pb}(t_{Terre}).$
Calculer la quantité $N_{U}(t_{Terre})$ de noyaux d'uranium.
b) Déterminer l'âge $t_{Terre}$ de la Terre.
Exercice 6 Fusion Deutérium Tritium
La fusion nucléaire, c'est le Diable et le Bon Dieu !
Le Bon Dieu dans les étoiles où elle fait naître tous les atomes, jusqu'à ceux de la vie.
Mais le Diable sur Terre où elle fut utilisée à fabriquer des bombes qui pourraient tout anéantir, à commencer par la vie.
Mais alors que le diable de la destruction thermonucléaire semble rentrer dans sa boîte, la fusion nucléaire contrôlée dans les réacteurs civils ouvre des perspectives de développement économique durable à très long terme.
Paul-Henri Rebut,
L'énergie des étoiles-la fusion nucléaire contrôlée Éditions Odile Jacob $1999$ (dos de couverture).
Notations utilisées :
$-\ $ Particules ou noyaux $_{Z}^{A}X$ : $_{1}^{1}H$, $_{2}^{4}He$, $_{-1}^{0}e$, $_{0}^{1}n$, $_{1}^{1}p.$
$-\ $ Masse de la particule ou du noyau $_{Z}^{A}X$ : $m\left(_{Z}^{A}X\right).$
$-\ $ Énergie de liaison du noyau $$_{Z}^{A}X$ : $E_{\ell}\left(_{Z}^{A}X\right).$
1) Isotopie
1) a) Qu'appelle-t-on isotopes ?
1) b) Dans la littérature scientifique, on mentionne souvent :
$-\ $ le deutérium $D$ dont le noyau contient $1$ proton et $1$ neutron ;
$-\ $ le tritium $T$ dont le noyau contient $1$ proton et $2$ neutrons.
Comment doit-on noter $($dans la notation $_{Z}^{A}X)$ les noyaux $D$ et $T$ ?
A quel élément chimique appartiennent-ils ?
2) Radioactivité
2) a) Qu'est-ce qu'un noyau radioactif ?
2) b) Le tritium $T$ est radioactif $\beta^{-}.$
Écrire l'équation de la désintégration de $T$ $($en utilisant la notation $_{Z}^{A}X).$
2) c) Le tritium $T$ a une demie-vie $_{1/2}=12$ ans.
Que signifie cette affirmation ?
3) Fusion de noyaux
3) a) Qu'appelle-t-on réaction nucléaire de fusion ?
3) b) En utilisant la notation $_{Z}^{A}X.$, écrire l'équation nucléaire de la fusion $DT$, c'est-à-dire de la fusion entre un noyau de deutérium et un noyau de tritium, au cours de laquelle se forme un noyau d'hélium $_{2}^{4}He.$
Exprimer l'énergie $\Delta\,E$ qui peut être libérée par cette réaction en fonction des énergies de masse $E_{m}\left(_{Z}^{A}X\right)$ des particules (ou des noyaux) qui interviennent.
3) c) Exprimer la masse $m\left(_{Z}^{A}X\right)$ du noyau $_{Z}^{A}X$ en fonction de $m_{p}$, $m_{n}$, $Z$, $A$ et de l'énergie de liaison $E_{\ell}\left(_{Z}^{A}X\right).$
Pour la réaction de fusion envisagée, en déduire l'expression de $\Delta\,E$ en fonction des énergies de liaison.
3) d) On donne les valeurs des énergies de liaison des noyaux suivants :
$-\ \ E_{\ell}(D)=2.224\,Me\,V$ ;
$-\ \ E_{\ell}(T)=8.481\,Me\,V$ ;
$-\ \ E_{\ell}(42He)=28.29\,Me\,V.$
Calculer numériquement la valeur de $\Delta\,E.$
4) Conditions de la fusion $DT$
La fusion n'a lieu que si les deux noyaux sont en contact.
4) a) Les noyaux $D$ et $T$ se repoussent.
Pourquoi ?
4) b) Pour que la fusion ait lieu, il faut que les noyaux $D$ et $T$ entrent en contact.
Celui-ci n'est possible que si l'agitation thermique, c'est-à-dire l'énergie cinétique $E_{C}$ des noyaux, est suffisamment.
Exercice 7 Temps caractéristiques en physique
Les parties $1$, $2$ et $3$ de cet exercice sont indépendantes, toutefois l'objectif de cette étude expérimentale consiste, pour trois systèmes différents :
$\bullet\ $ d'une part à étudier un « temps » défini comme « temps caractéristique »
$\bullet\ $ d'autre part, à observer l'influence éventuelle sur ce temps caractéristique :
des grandeurs caractéristiques ; de conditions initiales ; et de paramètres extérieurs.
Pour chacun des phénomènes, les grandeurs caractéristiques, les conditions initiales et les paramètres extérieurs envisagés sont précisés dans le tableau de données.
Un échantillon de matière radioactive est placé dans la chambre d'un photomultiplicateur.
Un détecteur, associé au photomultiplicateur, mesure un nombre d'événements, pendant une durée $\Delta\,t$ déterminée.
On trace la courbe d'évolution du nombre d'événements mesuré par seconde $($noté $x)$, au cours du temps.
Soit $x_{0}$ la valeur de $x$ à l'instant choisi pour origine des dates.
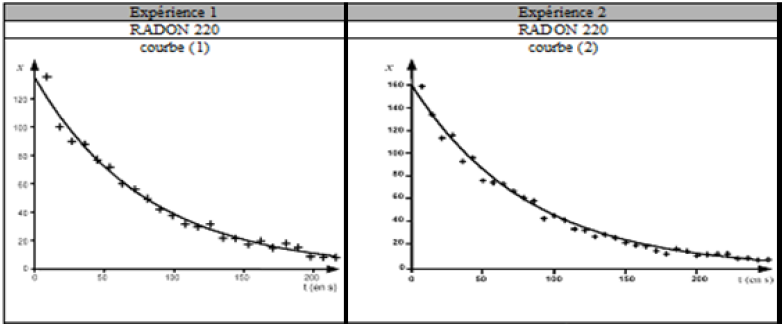
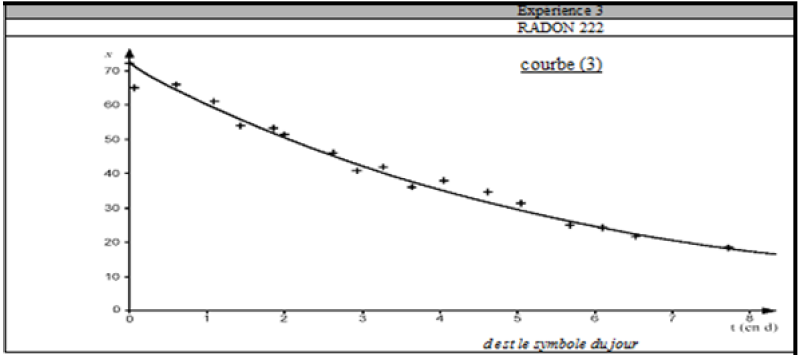
On réalise des mesures avec des échantillons de radon $_{86}^{220}Rn$ et de radon $_{86}^{222}Rn$ qui sont des émetteurs $\alpha.$
Le tableau ci-dessous résume les conditions expérimentales de cette étude :
$$\begin{array}{|c|c|c|c|} \hline &\text{Expérience 1}&\text{Expérience 2}&\text{Expérience 3}\\ \hline \text{Grandeurs caractéristiques du système :}&\text{radon }220&\text{radon }220&\text{radon }222\\ \text{nature du noyau}& & &\\ \hline \text{Conditions initiales :}&N_{0}&N'_{0}&N''_{0}\\ \text{population initialede noyaux radioactifs}& & &\\ N_{0}\neq N'_{0}\neq N''_{0}& & &\\ \text{Paramètres extérieurs}&\text{Aucune modification}&\text{Aucune modification}&\text{Aucune modification}\\\text{des paramètres extérieurs}&\text{des paramètres extérieurs}&\text{des paramètres extérieurs}&\text{des paramètres extérieurs}\\\hline \text{Temps caractéristique}&t_{1/2}=55.5\,s&t_{1/2}=55.5\,s&t_{1/2}= ?\text{(déterminé à la question 1.3.)}\\ \hline\end{array}$$
Les courbes correspondant à cette étude et donnant l'évolution de $x$ au cours du temps sont représentées en annexe
1) Définir le temps de demi-vie (ou demi-vie).
2) La loi de décroissance radioactive s'écrit sous la forme $N=N_{0}\cdot e^{-\lambda\,t}$ où : $N$ est le nombre de noyaux radioactifs présents à l'instant de date $t$, $N_{0}$ est le nombre de noyaux radioactifs présents à l'instant choisi pour origine des dates $t_{0}=0\,s$, $\lambda$ est la constante radioactive.
En utilisant la définition du temps de demi-vie, établir l'expression de $\lambda$ en fonction de $t_{1/2}.$
3) Dans le cas de l'expérience 3, déterminer graphiquement la valeur du temps de demi-vie.
La détermination devra apparaître clairement sur la courbe (3) de l'annexe
Pour cette détermination, on admettra que le nombre d'événements détectés par seconde, à l'instant de date $t$, est proportionnel au nombre de noyaux radioactifs présents dans l'échantillon, à cette même date.
Pour déterminer le temps de demi-vie, on peut alors utiliser la courbe $x=f(t)$ de la même façon que celle représentant le nombre de noyaux radioactifs présents dans l'échantillon en fonction du temps.
4) En justifiant les réponses à partir des données du tableau et du résultat obtenu à la question
5) Préciser :
$-\ $ Si les grandeurs caractéristiques ont une influence sur la valeur du temps de demi-vie ;
$-\ $ Si les conditions initiales ont une influence sur la valeur du temps de demi-vie.
Exercice 8
Tableaux de données :
$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|} \hline \text{Particule}&\text{Neutron}&\text{Hydrogène}&\text{Hydrogène}&\text{Hydrogène}&\text{Hélium}&\text{Hélium}&\text{Uranium}&\text{Xénon}&\text{Strontium}\\ \text{ou Noyau}& &1\text{ ou proton}&2\text{ ou Deutérium}&3\text{ ou Tritium}&3&4&235& &\\ \hline \text{Symbole}&_{0}^{1}n&_{1}^{1}H&_{1}^{2}H&_{1}^{3}H&_{2}^{3}H&_{2}^{4}H&_{92}^{235}U&_{54}^{A}Xe&_{Z}^{94}Sr\\ \hline \text{Masse en }u&1.00866&1.00728&2.01355&3.01550&3.01493&4.00150&234.9942&138.8892&93.8945\\ \hline \end{array}$$
$$\begin{array}{|c|c|} \hline \text{Unité de masse atomique}&u=1.66\times 10^{-27}kg\\ \hline \text{Énergie de masse de l'unité de masse atomique}&E=931.5\,MeV\\ \hline \text{Électronvolt}&1\,eV=1.60\times 10^{-19}J\\ \hline \text{Vitesse de la lumière dans le vide}&c=3.00\times 10^{8}m\cdot s^{-1}\\ \hline \text{Nombre d'Avogadro}&N=6.02\cdot 10^{23} \\ \hline \end{array}$$
I. La combustion du butane $C_{4}H_{8}$ (gaz de ville) :
L'énergie dégagée au cours de la combustion complète d'une mole de butane est $Q=2878\cdot10^{3}J$ ça veut dire que la combustion complète de $56\,g$ de butane dégage une énergie de $2878\cdot10^{3}J.$
II. Fission nucléaire
Une centrale nucléaire est une usine de production d'électricité.
Actuellement ces centrales utilisent la chaleur libérée par des réactions de fission de l'uranium $235$ qui constitue le "combustible nucléaire".
Cette chaleur transforme de l'eau en vapeur.
La pression de la vapeur permet de faire tourner à grande vitesse une turbine qui entraîne un alternateur produisant l'électricité.
Certains produits de fission sont des noyaux radioactifs à forte activité et dont la demi-vie peut être très longue.
1) Définir le terme demi-vie.
2) Le bombardement d'un noyau d'uranium $235$ par un neutron peut produire un noyau de strontium et un noyau de xénon selon l'équation suivante :
$$_{92}^{235}U\ +\ _{0}^{1}n\ \rightarrow\ _{Z}^{94}Sr\ +\ _{54}^{A}Xe\ +\ 3_{0}^{1}n$$
a) Déterminer les valeurs des nombres $A$ et $Z.$
b) Calculer en $MeV$ puis en joule l'énergie libérée par la fission d'un noyau d'uranium $235.$
Déduire L'énergie libérée en joule par la fission d'une mole d'uranium $235.$
c) Quelle est la masse de butane qu'on doit utiliser au cours d'une combustion complète pour produire la même quantité d'énergie libérée lors de la fission de $235\,g$ d'uranium $^{235}U.$
III. Fusion nucléaire
La fusion est la source d'énergie du soleil et des autres étoiles.
Pour obtenir une réaction de fusion, il faut rapprocher suffisamment deux noyaux qui se repoussent, puisqu'ils sont tous deux chargés positivement.
Une certaine énergie est donc indispensable pour franchir cette barrière et arriver dans la zone, très proche du noyau, où se manifestent les forces nucléaires capables de l'emporter sur la répulsion électrostatique.
La réaction de fusion la plus accessible est la réaction impliquant le deutérium et le tritium.
C'est sur cette réaction que se concentrent les recherches concernant la fusion contrôlée.
La demi-vie du tritium consommé au cours de cette réaction n'est que de quelques années.
De plus il y a très peu de déchets radioactifs générés par la fusion et l'essentiel est retenu dans les structures de l'installation.
1. Le deutérium de symbole $_{1}^{2}H$ et le tritium de symbole $_{1}^{3}H$ sont deux isotopes de l'hydrogène.
1.1 Définir le terme de noyaux isotopes.
1.2 Donner la composition de ces deux noyaux.
2. Qu'appelle-t-on réaction de fusion ?
3. Écrire l'équation de la réaction nucléaire entre un noyau de Deutérium et un noyau de Tritium sachant que cette réaction libère un neutron et un noyau noté $_{Z}^{A}X.$
Préciser la nature du noyau $_{Z}^{A}X.$
4. Montrer que l'énergie libérée au cours de cette réaction de fusion est de $17.6\,MeV.$
Quelle est l'énergie libérée par la fusion d'une mole de tritium.
5. Quelle est la masse de butane qu'on doit utiliser au cours d'une combustion complète pour produire la même quantité d'énergie libérée lors de la fusion d'une mole de tritium.
6. A-t-on intérêt d'implanter en Tunisie un réacteur nucléaire.
Citer les avantages et les inconvénients.
Exercice 9
On donne pour tout l'exercice :
$m(Bi)=210.0535\,U$
$M(Po)=210.0362\,u$ ;
$M(Pb)=206.0295\,u$ ;
$m_{\alpha}=4.0015\,u$ ;
$m_{n}=1.0086\,u$ ;
$m_{p}=1.0072\,u$
$1\,Mev=1.6\cdot10^{-13}J$ ;
$1\,u=1.66\cdot10^{-27}kg=931.5\,Mev$ ;
$1$ jour$=86400\,s.$
Les parties $A$ et $B$ sont indépendantes.
A. un isotope du bismuth $_{Z}^{A}Bi$ est radioactif émetteur $\beta^{-}$ sa désintégration donne un noyau de polonium $_{84}^{210}Po.$
1) a) Écrire l'équation de la réaction nucléaire de désintégration du bismuth en précisant les lois utilisées.
b) Cette désintégration est-elle provoquée ou spontanée ?
Justifier la réponse.
c) Quelle est l'origine de la particule $\beta^{-}$ émise.
2) a) Calculer, en $Mev.$ nucléon$^{-1}$, l'énergie de liaison par nucléon $E_{1}$ du noyau de bismuth utilisé.
b) Sachant que l'énergie de liaison du noyau de polonium est $E_{l_{2}}=1539.02\,Mev$, comparer la stabilité des noyaux de $_{Z}^{A}Bi$ et de $_{84}^{210}Po.$
3) A l'instant initial $t=0$, on considère un échantillon de bismuth de masse $m_{0}=1\,g$, soit $m(t)$ la masse du bismuth restant à la date $t$ $(t$ exprimée en jours$).$
a) donner l'expression du nombre de noyaux $N$ existant dans un échantillon de masse $m$ de bismuth en fonction de $m$, $M$ (masse molaire du bismuth) et $N$ (nombre d'Avogadro).
b) En appliquant la loi de décroissance radioactive, exprimer $m(t)$ en fonction de $m_{0}$, de la constante de désintégration radioactive $\lambda$ et de $t.$
c) Donner la définition de la période radioactive $T$ du bismuth puis calculer sa valeur (en jours) sachant que $m(t+10)=\dfrac{m(t)}{4}$ $(t$ : en jours$).$
d) Quelle est la masse restante de bismuth à la date $t=18$ jours.
e) Définir l'activité d'une substance radioactive.
Déterminer l'activité radioactive $A_{0}$ de l'échantillon à la date $t=0$, puis déduire l'activité $A$ à la date $t=18$ jours $($il faut donner $A$ et $A_{0}$ en $B_{q})$
B. Le polonium $_{84}^{210}Po$ est radioactif émetteur $\alpha.$
1) Écrire l'équation de la réaction de désintégration $\alpha$ du $_{84}^{210}Po$ sachant qu'il conduit à un isotope du plomb $P_{b}.$
2) Calculer, en $Mev$, l'énergie $E$ libérée par cette réaction nucléaire.
3) En admettant que l'énergie $E$ libérée est répartie entre la particule $\alpha$ et le noyau de plomb sous forme d'énergie cinétique et que le rapport des énergies cinétiques de $\alpha$ et de $P_{b}$ est égal à l'inverse du rapport de leurs masses $\left(\dfrac{E_{C_{\alpha}}}{E_{C_{Pb}}}=\dfrac{m_{Pb}}{m\alpha}\right).$
Calculer en $Mev$ l'énergie cinétique de la particule $\alpha$ émise et celle $E_{C_{Pb}}$ du noyau de plomb, puis déduire la vitesse $v_{\alpha}$ de la particule $\alpha.$
4) En réalité, la particule $\alpha$ émise possède une énergie cinétique $E'_{C_{\alpha}}$ tel que $E'_{C_{\alpha}}<E_{C_{\alpha}}.$
a) Expliquer brièvement cette différence.
b) Sachant que l'énergie du photon $\lambda$ émis est $W_{\lambda}=0.918\,Mev$, déduire la valeur de $E'_{C_{\alpha}}$ et la longueur d'onde du photon $\lambda.$

Commentaires
el hadji (non vérifié)
ven, 08/14/2020 - 15:35
Permalien
demande de correction
MOUNOUA Herzog ... (non vérifié)
mer, 03/02/2022 - 08:10
Permalien
Demande de correction des deux premiers exercices de la radioact
Moustapha Gueye (non vérifié)
lun, 04/26/2021 - 23:55
Permalien
Demande de correction de la série d'exercices
Mostafa (non vérifié)
mer, 05/19/2021 - 02:32
Permalien
C t juste pour mon fils
musta123aoura@g... (non vérifié)
lun, 12/20/2021 - 10:09
Permalien
corrigé des exercices
Justin AMEGNIZIAN (non vérifié)
lun, 06/09/2025 - 01:22
Permalien
Pour ma révisions
Ajouter un commentaire