Poids d'un corps : relation poids masse - 4e
Classe:
Quatrième
I- Texte introductif
1. Se promenant dans un verger, Moussa voit tomber des fruits mûrs. Il se pose alors les questions suivantes :
Qu'est ce qui fait tomber ces fruits ?
$\centerdot\ $ Pourquoi ces fruits ne s'envolent-ils pas ?
2. Vous disposez d'un aimant et d'un clou. Placez le clou près de l'aimant.
$\centerdot\ $ Qu'observez-vous ?
$\centerdot\ $ Comment l'expliquez-vous ?
$\centerdot\ $ Ces observations peuvent-elles nous permettre de répondre aux questions de Moussa ?
II- Contenus
Les fruits et les feuilles tombent, car ils sont attirés par la terre.
De même le clou placé près de l'aimant est attiré par ce dernier.
1. Le poids d'un objet
1.1. Mise en évidence du poids d'un objet
La photo 1 montre l'allongement du ressort sous l'action du poids de l'objet.
La photo 2 montre la déformation de la tige flexible sous l'action du poids de l'objet
I-2. Définition du poids d'un objet
Le poids d'un objet est l'attraction que la terre exerce sur cet objet.
1.3. Caractéristiques du poids
1.3.1. Droite d'action du poids
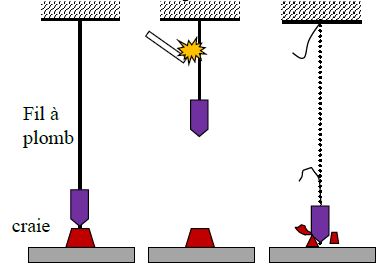
Le poids agit suivant une droite verticale appelée droite d'action du poids.
1.3.2. Sens du poids
Après la rupture du fil, l'objet tombe en chute libre suivant la direction du fil.
L'action du poids a pour direction celle du fil qui définit la verticale. Son sens est vers le bas.
Les objets attirés par la terre partent du haut vers le bas :
On dit que le poids a un sens.
Le sens du poids est du haut vers le bas.
1.3.3. Point d'application du poids
Pour déterminer, par exemple, le point d'application du poids d'une plaque de forme quelconque, on la suspend par un de ses points et on trace la verticale passant par ce point.
On recommence l'expérience pour plusieurs autres points.
On observe alors que toutes les verticales tracées sont concourantes à un point $G.$ Le point $G$, point de rencontre des verticales, est le point d'application du poids.
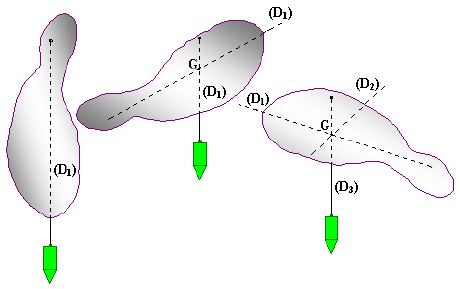
Ce point $G$ est appelé centre de gravité de la plaque.
La plaque tombe toujours du coté où se situe le centre de gravité.
Le poids de l'objet agit au centre de gravité.
Le centre de gravité est appelé point d'application du poids.
1.3.4. Intensité du poids

La photo 1 montre un ressort au bout duquel, on a accroché un plateau vide, on repère la position de l'index à une graduation de 20.9 cm.
La photo 2 montre une masse $A$ posée sur le plateau, on repère l'index à 24.3 cm, ce qui correspond à un allongement de 3.4 cm du ressort.
La photo 3 montre une masse B double de $A$, posée sur le poids, on repère l'index à 27.7 cm, soit un allongement 6.8 cm.
L'objet B provoque un allongement plus important du ressort que celui provoqué par l'objet
$A$ : le poids de $B$ est plus intense que le poids de $A.$
Le poids d'un objet se caractérise par son intensité qui donne sa valeur numérique.
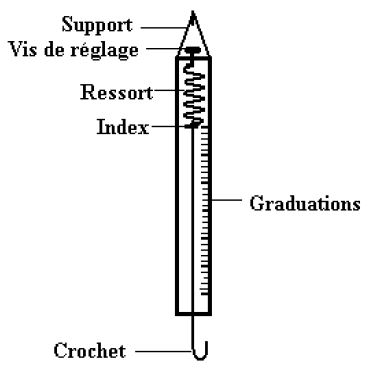
L'intensité du poids d'un objet se mesure à l'aide d'un appareil appelé dynamomètre.
L'intensité du poids est exprimée en newton dans le système international. Son symbole est $N.$
Photo d'un dynamomètre indiquant le poids d'un objet
Représentation vectorielle
Le poids d'un objet possède quatre caractéristiques :
$\rhd$ Sa droite d'action qui est verticale
$\rhd$ Son sens qui est du haut vers le bas
$\rhd$ Un point d'application : le centre de gravité de l'objet
$\rhd$ Son intensité, c'est à dire sa valeur numérique en newtons.
On peut représenter sur un schéma ces quatre caractéristiques du poids.
N.B.
L'intensité est représentée alors par un segment dont la longueur est déterminée selon une échelle.
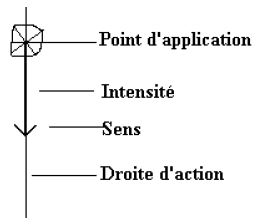
Le schéma obtenu est appelé vecteur poids noté $\vec{P}$ :
le poids est une grandeur vectorielle.
Schéma d'un dynamomètre vertical
II- Relation entre l'intensité du poids et la masse d'un objet
II-1. Tableau de mesures
On dispose de masses marquées $A\;,\ B\;,\ C\text{ et }D$ de masses respectives $m_{A}\;,\ m_{B}\;,\ m_{C}\text{ et }m_{D}.$
On mesure les intensités respectives des poids de ces objets à l'aide d'un dynamomètre, puis on complète le tableau suivant :
$$\begin{array}{|c|c|c|c|c|} \hline \text{Corps}&A&B&C&D\\ \hline \text{Masses}& m_{A}=\ldots & m_{B}=\ldots & m_{C}=\ldots & m_{D}=\ldots\\ \hline \text{Intensité du poids}& P_{A}=\ldots & P_{B}=\ldots & P_{C}=\ldots & P_{D}=\ldots\\ \hline \end{array}$$
$$\begin{array}{|c|c|c|c|c|} \hline \text{Corps}&A&B&C&D\\ \hline \text{Rapport}\dfrac{P}{m}&\ldots &\ldots &\ldots &\ldots\\ \hline \end{array}$$
On obtient des résultats sensiblement égaux ; on peut écrire :
$\dfrac{P_{A}}{m_{A}}=\dfrac{P_{B}}{m_{B}}=\dfrac{P_{C}}{m_{C}}=\dfrac{P_{D}}{m_{D}}=\text{constante}$
La masse et l'intensité du poids sont proportionnelles.
Le rapport $\dfrac{P}{m}$ est appelé l'intensité de la pesanteur.
On la note $g.$
II-3. Relation entre le poids et la masse
Le rapport $\dfrac{P}{m}=g$ conduit à la relation suivante : $P=m\,g$
L'intensité de la pesanteur $g$ s'exprime en newton par kilogramme $\left( N\cdot kg^{-1}\right)$ dans le système international.
II-4. L'intensité de la pesanteur varie en fonction du lieu.
La masse d'un objet étant constante, l'intensité de son poids dépend du lieu.
$\centerdot$ La valeur de $g$ dépend de la latitude et de l'altitude.
Exemple :
$\rhd$ sur la surface de la terre : $g=9.78\,N\cdot kg^{-1}$ à Dakar et $g=9.81\,N\cdot kg^{-1}$ à Paris.
Résumé
Le poids d'un objet est l'attraction exercée par la terre sur cet objet.
Le poids possède quatre caractéristiques qui sont :
$\rhd$ Sa droite d'action : droite selon laquelle le poids agit.
C'est la verticale du lieu où se trouve l'objet.
$\rhd$ Son sens : sens du mouvement que peut provoquer cette attraction.
Son sens est du haut vers le bas
$\rhd$ Son point d'application : endroit où le poids s'applique.
C'est le centre de gravité de l'objet attiré.
$\rhd$ Son intensité : renseigne sur la valeur de cette attraction.
Elle se mesure à l'aide d'un dynamomètre et s'exprime en newton de symbole $N.$
Le poids est une grandeur vectorielle.
Il est représenté par un vecteur.
L'intensité du poids est proportionnelle à la masse de l'objet.
L'intensité du poids est reliée à la masse par la relation : $P=m\,g$
Lecture : La pomme de Newton
Tout le monde connaît l'histoire de la pomme de Newton.
Le jeune savant reçoit sur la tête une pomme, et hop, il en déduit la loi de la Gravitation Universelle !
Cette caricature, dont personnellement j'adore la mise en scène sous le crayon de Gotlib, illustre bien le perpétuel éveil de l'esprit scientifique.

En effet, en 1666 et 1667, le jeune bachelier Isaac N. réside à la campagne, loin de Londres où sévit une épidémie de peste entrecoupée d'épisodes de grippe (cette dernière maladie avait déjà tué à Gravesend la jeune Rebecca Rolfe, née Mataoka, plus connue par son surnom amérindien de Pocahontas.
Bon, d'accord, ça n'a rien à voir, et c'était en 1616, mais j'avais envie de le dire, c'est tout).
Il découvre les joies des promenades bucoliques et un soir, dans son verger de Woolsthorpe (Lincolnshire), il observe la chute d'une pomme, alors que la Lune brille dans le ciel.
Connaissant la nature intrinsèquement proche de ces deux corps, Newton se pose la question :
Pourquoi la Lune ne tombe-t-elle pas elle aussi ?
La réponse le frappe avec une évidence soudaine :
Bien sûr, la Lune tombe ! Sinon, elle s'éloignerait de la Terre à tout jamais, emportée par sa vitesse.
Elle est retenue sur son orbite par une force sans support physique, la gravitation.
En quelques instants, la formule est établie, puis peaufinée longuement, pour devenir une phrase bien connue de tous ceux que la physique amuse et de tous ceux que la physique rebute.
Cette phrase définissant l'attraction universelle, vous la connaissez ?
Mais si, rappelez-vous : "Les autres s'attirent de
façon proportionnelle au produit de leur masse et
inversement proportionnelle au carré de la
distance qui les sépare."
On peut traduire par une formule donnant la force
d'attraction mutuelle $F$ qui s'exerce entre les masses
$m_{1}$ et $m_{2}$ séparées de la distance $d.$
Dans cette formule, $G$ est une constante universelle, appelée constante de gravitation $\left(\text{valeur }6.672\cdot 10^{-11}N\,m^{2}kg^{-2}\right).$
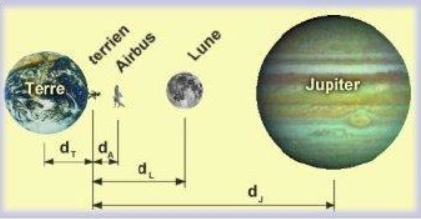
La Terre, masse $5.98\cdot 10^{24}kg$ à une distance (rayon) de 6 378 000 m un terrien moyen, type ascenseur (masse 70 kg) un Airbus, masse 100 000 kg à une distance de 6 000 m
la Lune, masse $7.35\cdot 10^{22}kg$ à une distance de 384 000 000 m Jupiter, masse $1.9\cdot 10^{28}kg$ à une distance de 778 300 000 000 m (demi-grand axe).
la formule donne la force exercée sur le terrien par ces différents corps.
Terre : $686.572\,N(69.987\,kg)$ « Lâche pas ton béret, Maurice ! »
avion : $1.167\cdot 10^{-10}N(0.0000000119\,g)$
Lune : $0.00232\,N(0.237\,g)$
Jupiter : $1.464\cdot 10^{-4}N(0.0149\,g)$
Source:
irempt.ucad.sn

Commentaires
Mohamed diop (non vérifié)
sam, 04/18/2020 - 15:43
Permalien
C'est très intéressant
fatou kiné mara (non vérifié)
mar, 09/08/2020 - 00:19
Permalien
ouais t'as raison
Mamita (non vérifié)
jeu, 04/29/2021 - 20:45
Permalien
Maths
Kimberly (non vérifié)
mer, 01/04/2023 - 20:47
Permalien
vérité
Astou diaw (non vérifié)
jeu, 03/04/2021 - 23:05
Permalien
Machallah ❤️
Antoine (non vérifié)
dim, 04/11/2021 - 16:21
Permalien
demande
ndeye courba Al... (non vérifié)
ven, 02/21/2025 - 22:41
Permalien
demande
Antoine (non vérifié)
dim, 04/11/2021 - 16:21
Permalien
demande
Astou gawane toure (non vérifié)
sam, 04/24/2021 - 00:34
Permalien
Tres intressant
Anonyme (non vérifié)
mer, 07/14/2021 - 23:18
Permalien
Ces tres important pour un
Anonyme (non vérifié)
mer, 07/14/2021 - 23:18
Permalien
Ces tres important pour un
Touba (non vérifié)
jeu, 10/21/2021 - 17:37
Permalien
Pourquoi on ne peut plus
Amy Traore (non vérifié)
lun, 02/13/2023 - 23:32
Permalien
JE TTROUVE SUPER BIEN BREF
Amy Traore (non vérifié)
lun, 02/13/2023 - 23:32
Permalien
JE TTROUVE SUPER BIEN BREF
Anonyme (non vérifié)
mar, 03/14/2023 - 18:36
Permalien
Si la terre exerce une d
Anonyme (non vérifié)
jeu, 03/07/2024 - 22:31
Permalien
tres bonne question mon ami
mouhamed al amine (non vérifié)
jeu, 03/07/2024 - 22:29
Permalien
devenir meilleur
Mame Diarra Ndiaye (non vérifié)
mer, 05/01/2024 - 23:46
Permalien
Devenir meilleur
Meri diop (non vérifié)
lun, 05/05/2025 - 00:03
Permalien
Merci est ce que un prof de
Ajouter un commentaire