Vous êtes ici

Niveaux d'énergie d'un atome - Ts

Classe:

Terminale

Un atome émet ou absorbe des radiations sous forme d'ondes électromagnétiques qui peuvent appartenir au domaine de l'ultraviolet, du visible, de l'infrarouge. L'ensemble de ces radiations constitue un spectre dont l'étude permet d'identifier l'atome considéré.

I. Spectre atomique

Le spectre atomique peut être obtenu à l'aide d'un spectroscope à prisme ou à réseau. On peut observer des spectres d'émission et des spectres d'absorption.

I.1. Spectres d'émission

Pour déterminer le spectre d'émission d'un atome, on l'excite en lui fournissant de l'énergie. L'atome peut alors émettre de la lumière dont l'analyse permet d'observer des raies fines claires, sur un fond noir, correspondant à certaines longueurs d'onde, caractéristiques de l'atome considéré.

Ces raies fines claires correspondent aux radiations émises.

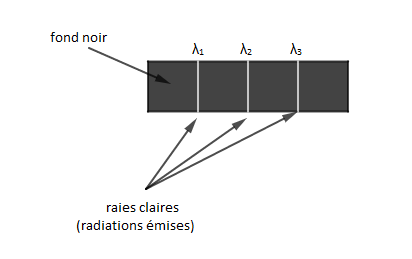
Le spectre d'émission est constitué par des rayonnements fins clairs sur un fond noir.

I.1. Spectres d'absorption

Pour déterminer le spectre d'absorption d'un atome, on fait analyser de la lumière blanche qui a traversé de la substance constituée par cet atome. On constate alors des raies noires, sur un fond clair, correspondant aux longueurs d'onde qu'émettrait cette substance si elle était excitée.

En examinant les radiations manquantes, à la sortie de la substance, on constate qu'elles correspondent à celles absorbées par les atomes de cette substance.

Donc, ces raies noires correspondent aux radiations absorbées.

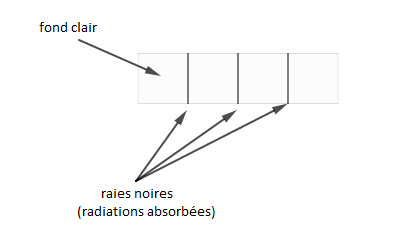
Le spectre d'absorption est caractérisé par des rayonnements sombres, sur un fond clair.

II. Niveaux d'énergie

L'énergie électromagnétique étant émise ou absorbée par un atome, l'énergie d'un atome est quantifiée : un atome possède des niveaux d'énergie

$E_{n}.$

Quand un atome est dans son niveau d'énergie le plus bas

$(n=1)$ , il est dans son état fondamental.

Lorsqu'il est dans un niveau supérieur

$(n=2\;,\ 3\;,\ ...)$ , il est dans un état excité.

Les niveaux d'énergie sont représentés dans un diagramme énergétique.

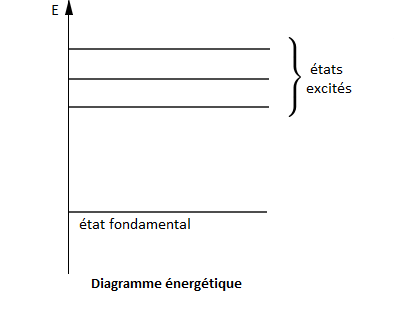
II.1. Excitation d'un atome

Un atome peut passer de son état fondamental à un état excité par apport d'énergie.

L'énergie passe alors du niveau d'énergie

$E_{n}$ au niveau d'énergie

$E_{p}$ par absorption d'un photon d'énergie

$h\nu_{_{n,p}}=E_{p}-E_{n}=\dfrac{hc}{\lambda_{_{n,p}}}\quad\text{si }\ E_{p}>E_{n}$

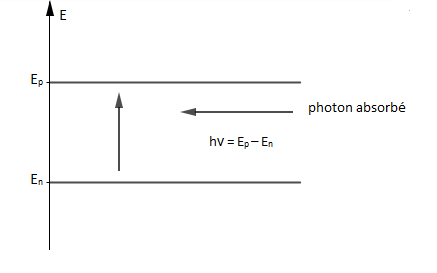
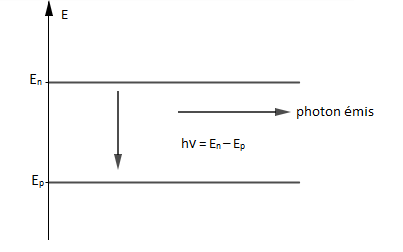
II.2. Désexcitation d'un atome

Tout atome a tendance, après excitation, à revenir spontanément à un état de niveau d'énergie inférieur plus stable en émettant un photon.

L'énergie passe alors du niveau d'énergie

$E_{n}$ au niveau d'énergie

$E_{p}$ par émission d'un photon d'énergie

$h\nu_{_{n,p}}=E_{n}-E_{p}=\dfrac{hc}{\lambda_{_{n,p}}}\quad\text{si }\ E_{n}>E_{p}$

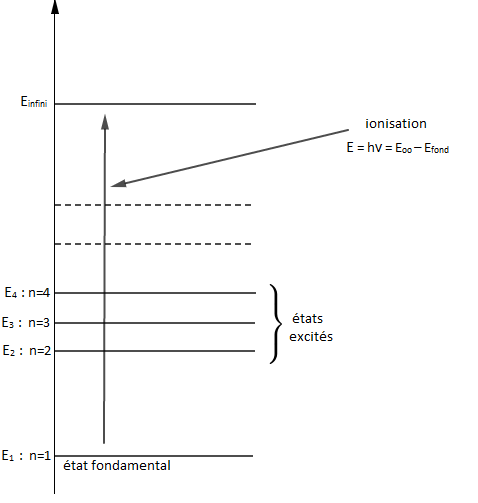
II.3. Ionisation d'un atome

Un atome est dans un état ionisé lorsque l'énergie apportée est assez grande pour lui arracher l'électron (l'électron sera infiniment éloigné du proton).

Ainsi, lorsque

$n$ tend vers l'infini, le niveau d'énergie

$E_{n}$ tend vers

$E_{\infty}=0.$

Remarque

Des atomes ionisés au point qu'il ne leur reste qu'un seul électron deviennent des ions hydrogénoïdes.

III. L'atome d'hydrogène

Les niveaux d'énergie de l'atome d'hydrogène sont donnés par la relation :

$E_{n}=-\dfrac{E_{0}}{n^{2}}$

où

$E_{0}=13.6\;eV\;;\ 1\;eV=1.6\;10^{-19}\;J\$ et

$\ n$ est un nombre entier non nul appelé nombre quantique principal.

$\cdot\ \ n=1$ correspond à l'état fondamental

$E_{1}=-13.6\;eV$

$\cdot\ \ n>1$ correspond aux états excités.

$\cdot\ \$ lorsque

$n\rightarrow +\infty\;;\ E_{n}\rightarrow 0$ l'atome est à l'état ionisé

Exemple

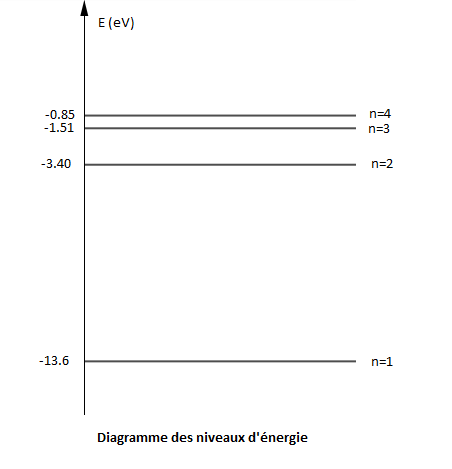
Les quatre premiers niveaux d'énergie ont pour valeur :

$E_{1}=-13.6\;eV\;;\ E_{2}=-3.40\;eV\;;\ E_{3}=-1.51\;eV\;;\ E_{4}=-0.85\;eV$

Remarque

L'énergie d'un hydrogénoïde de numéro atomique

$z$ , au niveau

$n$ , est donnée par :

$E_{n}=z^{2}E_{H}\$ où

$\ E_{H}$ est l'énergie de l'atome d'hydrogène de même niveau

$n.$

III.1. Les raies d'émission

La transition

$n\rightarrow p\;(n>p)$ correspond à l'émission d'un photon d'énergie

$h\nu_{_{n,p}}=E_{n}-E_{p}=\dfrac{hc}{\lambda_{_{n,p}}}$

avec :

$E_{n}=-\dfrac{E_{0}}{n^{2}}\$ et

$\ E_{p}=-\dfrac{E_{0}}{p^{2}}$ , soit :

$\dfrac{hc}{\lambda_{_{n,p}}}=-\dfrac{E_{0}}{n^{2}}+\dfrac{E_{0}}{p^{2}}=-E_{0}\left(\dfrac{1}{p^{2}}-\dfrac{1}{n^{2}}\right)$

Ce qui entraîne :

$\dfrac{1}{\lambda_{_{n,p}}}=\dfrac{E_{0}}{hc}\left(\dfrac{1}{p^{2}}-\dfrac{1}{n^{2}}\right)\;,\quad \nu_{_{n,p}}=\dfrac{E_{0}}{h}\left(\dfrac{1}{p^{2}}-\dfrac{1}{n^{2}}\right)\;,\quad \lambda_{_{n,p}}=\dfrac{c}{\nu_{_{n,p}}}$

$h=6.62\;10^{-34}\;J.s$ est la constante de Planck

$c=3\;10^{8}\;m.s^{-1}$ est la vitesse de la lumière dans le vide

$\dfrac{E_{0}}{hc}=R_{H}$ est la constante de Rydberg.

A.N :

$R_{H}=\dfrac{13.6\times 1.6\;10^{-19}}{6.62\;10^{-34}\times 3\;10^{8}}=1.10\;10^{7}$

Ainsi,

$R_{H}=1.10\;10^{7}\;m^{-1}$

Définition

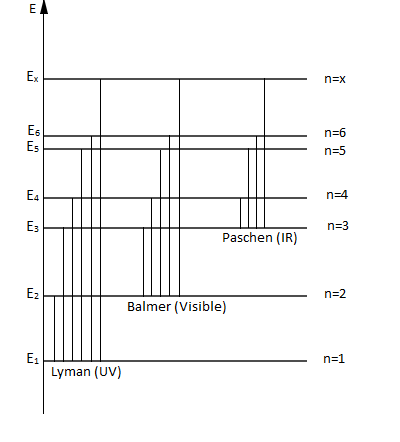
Une série de raies correspond aux transitions aboutissant au même niveau d'énergie.

C'est-à-dire ; à un niveau final

$p$ , correspond une infinité de valeurs de

$n$ , correspondant à une série de raies :

$\centerdot\ \ p=1\$ et

$\ n=2\;,\ 3\;,\ ...$ raies de la série de Lyman (ultraviolet)

$\centerdot\ \ p=2\$ et

$\ n=3\;,\ 4\;,\ ...$ raies de la série de Balmer (contient quatre raies dans le domaine du visible)

$\centerdot\ \ p=3\$ et

$\ n=4\;,\ 5\;,\ ...$ raies de la série de Paschen (infrarouge)

III.2. Énergie d'ionisation

L'énergie d'ionisation

$E_{\text{ion}}$ de l'atome d'hydrogène est l'énergie qu'il faut fournir pour arracher l'électron sans lui communiquer d'énergie cinétique. On a :

$E_{\text{ion}}=E_{\infty}-E_{1}=0-(-E_{0})=E_{0}$

L'énergie d'ionisation de d'hydrogène est donc de

$13.6\;eV$

III.3. Longueurs d'onde limites d'une série

$\centerdot\ \$ Longueur d'onde la plus courte $\lambda_{_{\ell}}$

Elle correspond à la transition de l'atome du niveau ionisé au niveau le plus bas :

$E_{\infty}-E_{bas}$

$-\ \$ Série de Lyman

$\dfrac{hc}{\lambda_{_{\ell}}}=E_{\infty}-E_{1}=13.6\;eV$

$\Rightarrow\ \lambda_{_{\ell}}=\dfrac{hc}{13.6\;eV}$

A.N :

$\lambda_{_{\ell}}=\dfrac{6.62\;10^{-34}\times 3\;10^{8}}{13.6\times 1.6\;10^{-19}}=9.1\;10^{-8}$

D'où,

$\lambda_{_{\ell}}=91\;\;nm$

$-\ \$ Série de Balmer

$\dfrac{hc}{\lambda_{_{\ell}}}=E_{\infty}-E_{2}=\dfrac{13.6\;eV}{2^{2}}=\dfrac{13.6\;eV}{4}$

$\Rightarrow\ \lambda_{_{\ell}}=\dfrac{4hc}{13.6\;eV}$

A.N :

$\lambda_{_{\ell}}=\dfrac{4\times 6.62\;10^{-34}\times 3\;10^{8}}{13.6\times 1.6\;10^{-19}}=36.4\;10^{-8}$

D'où,

$\lambda_{_{\ell}}=364\;\;nm$

$\centerdot\ \$ Longueur d'onde la plus grande $\lambda_{_{L}}$

Elle correspond à la plus petite valeur de

$n.$

$-\ \$ Série de Lyman : $p=1\;,\ n=2$

$\dfrac{1}{\lambda_{_{L}}}=R_{H}\left(\dfrac{1}{p^{2}}-\dfrac{1}{n^{2}}\right)=R_{H}\left(1-\dfrac{1}{4}\right)=\dfrac{3}{4}R_{H}$

$\Rightarrow\ \lambda_{_{L}}=\dfrac{4}{3}\times\dfrac{1}{R_{H}}$

A.N :

$\lambda_{_{L}}=\dfrac{4}{3}\times\dfrac{1}{1.10\;10^{7}}=1.216\;10^{-7}$

D'où,

$\lambda_{_{L}}=121.6\;\;nm$

$-\ \$ Série de Balmer : $p=2\;,\ n=3$

$\dfrac{1}{\lambda_{_{L}}}=R_{H}\left(\dfrac{1}{p^{2}}-\dfrac{1}{n^{2}}\right)=R_{H}\left(\dfrac{1}{4}-\dfrac{1}{9}\right)=\dfrac{5}{36}R_{H}$

$\Rightarrow\ \lambda_{_{L}}=\dfrac{36}{5}\times\dfrac{1}{R_{H}}$

A.N :

$\lambda_{_{L}}=\dfrac{36}{5}\times\dfrac{1}{1.10\;10^{7}}=6.545\;10^{-7}$

D'où,

$\lambda_{_{L}}=654.5\;\;nm$

Exercice d'application

On considère un atome de mercure dont quelques niveaux d'énergie ont pour valeur :

$E_{3}=-2.72\;eV\;;\ E_{2}=-3.75\;eV\;;\ E_{1}=-4.99\;eV\$ et

$\ E_{0}=-10.45\;eV$ (niveau fondamental)

1) Calculer les énergies des photons émis par l'atome de mercure lorsque celui-ci passe du niveau

$E_{3}$ au niveau

$E_{1}$ et du niveau

$E_{2}$ au niveau

$E_{0}.$

2) Quelles sont les longueurs d'onde

$\lambda_{_{3,1}}\$ et

$\ \lambda_{_{2,0}}$ des rayonnements émis ?

Dans quels domaines de radiations se trouvent ces deux longueurs d'onde ?

Résolution

1) Soit

$E_{n,p}$ l'énergie du photon émis lorsque l'atome passe d'un niveau

$n$ d'énergie

$E_{n}$ à un niveau

$p$ d'énergie

$E_{p}$ avec

$E_{p}<E_{n}.$

Alors, pour la transition du niveau 3 au niveau 1 on a :

$E_{3,1}=E_{3}-E_{1}$

A.N :

$E_{3,1}=-2.72\;eV+4.99\;eV=2.27\;eV$

D'où,

$\boxed{E_{3,1}=2.27\;eV}$

De la même manière, pour la transition du niveau 2 au niveau 0 on a :

$E_{2,0}=E_{2}-E_{0}$

A.N :

$E_{2,0}=-3.75\;eV+10.45\;eV=6.70\;eV$

Donc,

$\boxed{E_{2,0}=6.70\;eV}$

2) L'énergie d'un photon est reliée à la longueur d'onde par la relation :

$E_{n,p}=\dfrac{hc}{\lambda_{_{n,p}}}\quad\text{soit }\ \lambda_{_{n,p}}=\dfrac{hc}{E_{n,p}}$

A.N :

$\lambda_{_{3,1}}\dfrac{6.62\;10^{-34}\times 3\;10^{8}}{2.27\times 1.6\;10^{-19}}=5.48\;10^{-7}$

D'où,

$\boxed{\lambda_{_{3,1}}=548\;\;nm}$

On a :

$400\;nm<\lambda_{_{3,1}}<800\;nm$ alors, cette radiation fait partie du domaine du visible, le vert

$(500\;nm<\lambda_{_{3,1}}<570\;nm).$

De même pour

$\lambda_{_{2,0}}$ on a :

A.N :

$\lambda_{_{2,0}}\dfrac{6.62\;10^{-34}\times 3\;10^{8}}{6.70\times 1.6\;10^{-19}}=1.86\;10^{-7}$

Ainsi,

$\boxed{\lambda_{_{2,0}}=186\;\;nm}$

$\lambda_{_{2,0}}<400\;nm$ donc, cette radiation appartient au domaine de l'ultraviolet.

Auteur:

Diny Faye

Commentaires

Bandia (non vérifié)

mar, 10/22/2019 - 09:55

Permalien

Demande d'aide

Je voudrais avoir les leçons en pdf

répondre

alexis soropogui (non vérifié)

mer, 07/27/2022 - 19:58

Permalien

élève

les cours me conviennent

répondre

Ibrahima diallo (non vérifié)

mar, 09/01/2020 - 00:16

Permalien

Envie d avoir d aide

Sur votre page j aimerai que vous m aidiez

répondre

Anonyme (non vérifié)

sam, 04/16/2022 - 03:06

Permalien

Merci beaucoup

répondre

Anonyme (non vérifié)

sam, 06/22/2024 - 11:12

Permalien

Demande d'obtention des leçons de TS2 sous forme de PDF

Serait il possible d'avoir les leçons de TS2 sous forme de fichiers PDF s'il vous plaît ?

répondre

Babacar Ndiaye (non vérifié)

sam, 12/14/2024 - 12:17

Permalien

Je suis candidat libre au bac S2

Une très belle initiative

répondre

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.

Vous êtes ici

Niveaux d'énergie d'un atome - Ts

Formulaire de recherche

I. Spectre atomique

I.1. Spectres d'émission

I.1. Spectres d'absorption

II. Niveaux d'énergie

II.1. Excitation d'un atome

II.2. Désexcitation d'un atome

II.3. Ionisation d'un atome

III. L'atome d'hydrogène

III.1. Les raies d'émission

Définition

III.2. Énergie d'ionisation

III.3. Longueurs d'onde limites d'une série

Exercice d'application

Résolution

Commentaires

Demande d'aide

élève

Envie d avoir d aide

Merci beaucoup

Demande d'obtention des leçons de TS2 sous forme de PDF

Je suis candidat libre au bac S2

Ajouter un commentaire

Plain text