Mouvement d'un pendule conique - Ts

Classe:

Terminale

Illustration

Un pendule est constitué d'une boule de masse

$m$ et d'un fil sans raideur de longueur

$\ell$ et de masse négligeable. Il est en mouvement de rotation uniforme autour d'un axe

$\Delta.$

1) Donner l'expression de l'intensité

$T$ de la tension du fil.

2) Déterminer l'angle d'inclinaison

$\alpha$ du fil par rapport à la verticale.

3) Montrer que le fil ne peut s'écarter de sa position d'équilibre que si la vitesse angulaire

$\omega$ est supérieure à une valeur

$\omega_{_{0}}$ que l'on déterminera.

Étude du mouvement

On se place dans le repère terrestre supposé comme galiléen.

Le système étudié est le pendule assimilable à un point matériel.

Les seules forces extérieurs appliquées au système sont son poids

$\vec{p}=m.\vec{g}$ et la tension

$\vec{T}$ du fil.

En appliquant la deuxième loi de Newton, on a :

$\sum \vec{F}_{\text{ext}}=m\vec{a}$

Soit :

$\vec{T}+\vec{p}=m.\vec{a}$

Choisissons comme repère de projection, le repère d'origine

$O$ et d'axes

$(xx')$ et

$(yy')$ et supposons qu'à l'instant initial

$t_{0}=0$ , le centre d'inertie de la boule se trouve au point

$O.$

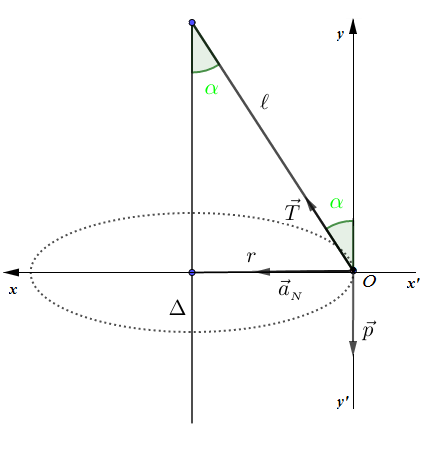
Le pendule étant en mouvement de rotation uniforme alors, sa trajectoire est curviligne de rayon de courbure

$r.$

De plus,

$\vec{a}_{_{T}}=\vec{0}.\$ D'où :

$\vec{a}=\vec{a}_{_{N}}$

Par suite, la relation

$\vec{T}+\vec{p}=m.\vec{a}$ devient :

$\vec{T}+\vec{p}=m.\vec{a}_{_{N}}$

Intensité de la tension du fil

En projetant la relation vectorielle

$\vec{T}+\vec{p}=m.\vec{a}_{_{N}}$ l'axe

$(xx')$ , on obtient :

$T.\sin\alpha=m.a_{_{N}}\qquad(1)$

Soit :

$\begin{array}{rcl} T&=&\dfrac{m.a_{_{N}}}{\sin\alpha}\quad\text{or },\ a_{_{N}}=\dfrac{v^{2}}{r}\ \text{ et }\ \sin\alpha=\dfrac{r}{\ell}\\ \\&=&\dfrac{m.v^{2}}{r}\times\dfrac{\ell}{r}\quad\text{or },\ v=r.\omega\\ \\&=&\dfrac{m.r^{2}.\omega^{2}.\ell}{r^{2}}\\ \\&=&m.\omega^{2}.\ell\end{array}$

D'où,

$\boxed{T=m.\omega^{2}.\ell}$

Angle d'inclinaison $\alpha$ du fil par rapport à la verticale

La projection suivant l'axe

$(yy')$ de la relation vectorielle

$\vec{T}+\vec{p}=m.\vec{a}_{_{N}}$ donne :

$m.g-T.\cos\alpha=0$

Soit :

$T.\cos\alpha=m.g\qquad(2)$

Ainsi,

$\cos\alpha=\dfrac{m.g}{T}\$ or,

$T=m.\omega^{2}.\ell$

Par suite,

$\begin{array}{rcl}\cos\alpha=\dfrac{m.g}{T}&=&\dfrac{m.g}{m.\omega^{2}.\ell}\\ \\&=&\dfrac{g}{\ell.\omega^{2}}\end{array}$

D'où,

$\boxed{\cos\alpha=\dfrac{g}{\ell.\omega^{2}}}$

Vitesse angulaire minimale $\omega_{_{0}}$

C'est la vitesse angulaire minimale avec laquelle il faut lancer le pendule afin qu'il s'écarte de la verticale.

On a :

$\begin{array}{rcl}\cos\alpha\leq 1&\Leftrightarrow&\dfrac{g}{\ell.\omega^{2}}\leq 1\\ \\&\Leftrightarrow&g\leq\ell.\omega^{2}\\ \\&\Leftrightarrow&\omega^{2}\geq\dfrac{g}{\ell}\\ \\&\Leftrightarrow&\omega\geq\sqrt{\dfrac{g}{\ell}}\end{array}$

Soit alors,