Vous êtes ici

Le dipôle (R, C) - Ts

Classe:

Terminale

Un dipôle

$(R\;,\;C)$ est l'association en série d'un condensateur de capacité

$C$ et d'un conducteur ohmique de résistance

$R.$

I. Le condensateur

I.1. Définition

Un condensateur est un ensemble constitué de deux conducteurs (armatures) séparés par un isolant appelé diélectrique qui peut être le vide.

Un condensateur est symboliquement représenté par :

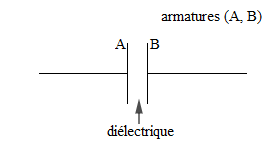
I.2. Capacité d'un condensateur

La charge du condensateur ou quantité d'électricité emmagasinée

$q$ et la tension

$u$ aux bornes du condensateur sont reliées par la relation :

$\boxed{q=C.u}$

$C$ est appelé capacité du condensateur. Elle s'exprime en Farads

$(F).$

Remarque : on utilise assez souvent les sous-multiples comme :

$\mu F=10^{-6}\;F\;;\ nF=10^{-9}\;F$ ou encore

$pF=10^{-12}\;F$

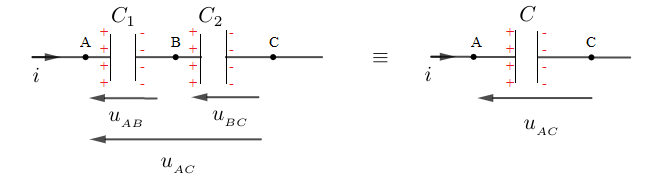
I.3. Association de condensateurs

I.3.1. Association en série

Soient deux condensateurs de capacité respective

$C_{1}$ et

$C_{2}$ montés en série alors, la capacité

$C$ du condensateur équivalent est telle que :

$\boxed{\dfrac{1}{C}=\dfrac{1}{C_{1}}+\dfrac{1}{C_{2}}}$

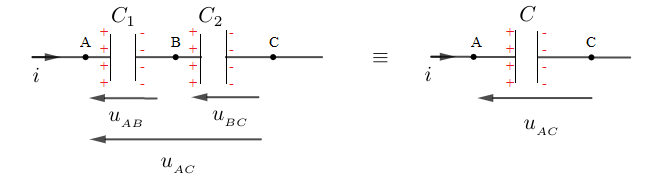
En effet, d'après la loi d'additivité des tentions on a :

$u_{_{AC}}=u_{_{AB}}+u_{_{BC}}$

Or,

$\ u_{_{AC}}=\dfrac{q}{C}\;,\ u_{_{AB}}=\dfrac{q_{_{A}}}{C_{1}}\$ et

$\ u_{_{BC}}=\dfrac{q_{_{B}}}{C_{2}}$

Donc,

$u_{_{AC}}=\dfrac{q}{C}=\dfrac{q_{_{A}}}{C_{1}}+\dfrac{q_{_{B}}}{C_{2}}$

Les condensateurs étant traversés par le même courant d'intensité

$i$ on obtient alors la même quantité d'électricité,

$q=q_{_{A}}=q_{_{B}}$ , pour chaque condensateur.

Par suite,

$\begin{array}{rcl} \dfrac{q}{C}&=&\dfrac{q_{_{A}}}{C_{1}}+\dfrac{q_{_{B}}}{C_{2}}\\ \\&=&\dfrac{q}{C_{1}}+\dfrac{q}{C_{2}}\\ \\&=&\left(\dfrac{1}{C_{1}}+\dfrac{1}{C_{2}}\right)q\end{array}$

D'où,

$\dfrac{1}{C}=\dfrac{1}{C_{1}}+\dfrac{1}{C_{2}}$

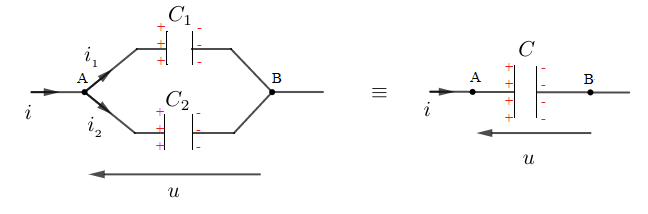
I.3.2. Association en parallèle

Soit maintenant les deux condensateurs de capacité respective

$C_{1}$ et

$C_{2}$ montés en parallèle alors, la capacité

$C$ du condensateur équivalent vérifie :

$\boxed{C=C_{1}+C_{2}}$

En effet, d'après la loi des nœuds on a :

$\begin{array}{rcrcl} i=i_{_{1}}+i_{_{2}}&\Rightarrow&q&=&q_{_{1}}+q_{_{2}}\\&\Rightarrow&Cu&=&C_{1}u+C_{2}u\\&\Rightarrow&Cu&=&(C_{1}+C_{2})u\end{array}$

D'où,

$C=C_{1}+C_{2}$

II. Charge d'un condensateur

Considérons le montage ci-dessous

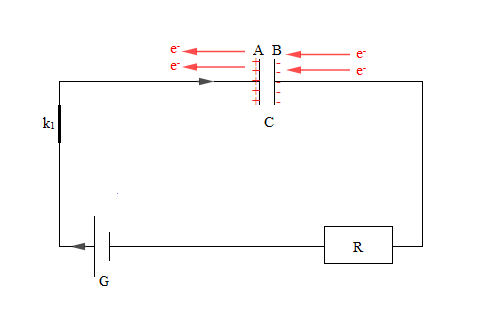
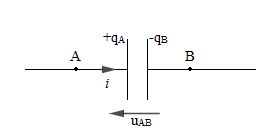
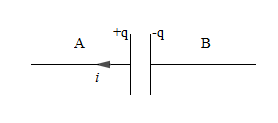
Alors, lorsque l'on branche un condensateur aux bornes d'un générateur celui-ci se charge. Les charges ne pouvant traverser l'isolant s'accumulent ainsi sur les armatures.

En effet, durant cette phase, les électrons se déplaçant dans le sens contraire du courant quittent alors l'armature

$A$ pour arriver à l'armature

$B.$

Ainsi,

$A$ sera chargée positivement et

$B$ négativement.

A chaque instant les charges portées par les armatures sont telles que :

$\boxed{q_{_{A}}=-q_{_{B}}=q}$

N.B : en convention récepteur

$i$ et

$u$ sont de sens opposés.

L'intensité

$i$ et la charge

$q$ du condensateur sont liées par la relation :

$\boxed{i(t)=\dfrac{\mathrm{d}q}{\mathrm{d}t}}$

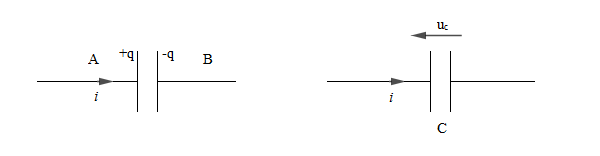
Ainsi,

$i>0\;,\ q$ augmente et

$\dfrac{\mathrm{d}q}{\mathrm{d}t}>0$

De plus, comme

$q=C.u$ alors, en remplaçant

$q$ par son expression puis en dérivant, on obtient :

$\boxed{i(t)=C.\dfrac{\mathrm{d}u}{\mathrm{d}t}}$

Équation différentielle

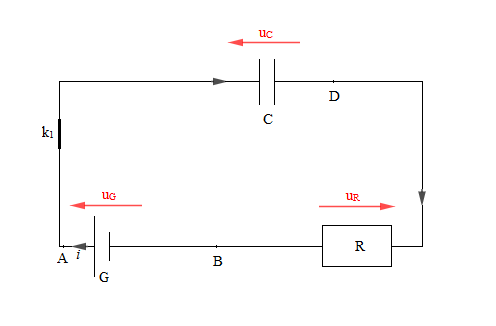
L'interrupteur

$k_{1}$ étant fermé, la charge du condensateur s'effectue alors à travers le résistor

$R.$

La loi d'additivité des tensions permet d'écrire :

$u_{_{AB}}=u_{_{AD}}+u_{_{DB}}$

avec

$u_{_{AB}}=u_{_{G}}=E\;,\ u_{_{AD}}=u_{_{C}}\$ et

$\ u_{_{DB}}=u_{_{R}}$

Or, d'après la loi d'Ohm on a :

$u_{_{R}}=R.i\quad(1)$

On obtient alors :

$u_{_{C}}+u_{_{R}}=E\quad(2)$

En convention récepteur

$i(t)=C.\dfrac{\mathrm{d}u_{_{C}}}{\mathrm{d}t}$ donc, en remplaçant successivement

$i(t)$ dans l'équation (1) puis

$u_{_{R}}$ dans l'équation (2), on obtient :

$\boxed{RC.\dfrac{\mathrm{d}u_{_{C}}}{\mathrm{d}t}+u_{_{C}}=E}$

On reconnait alors l'équation différentielle d'ordre 1 à coefficients constants en

$u_{_{C}}$ , qui peut encore s'écrire :

$\boxed{\dfrac{\mathrm{d}u_{_{C}}}{\mathrm{d}t}+\dfrac{u_{_{C}}}{RC}=\dfrac{E}{RC}}$

D'après le cours de mathématiques, cette équation, de la forme

$ay'+by=c\;,\ (a=1)$ , a pour solution

$y(t)=f_{2}(t)+f_{1}(t)$ avec

$f_{2}(t)$ solution générale de l'équation

$ay'+by=0\$ et

$\ f_{1}(t)$ une solution particulière de l'équation

$ay'+by=c.$

Alors :

$f_{2}(t)=k\mathrm{e}^{-bt}\$ et

$\ f_{1}(t)=\dfrac{c}{b}\$ avec

$b=\dfrac{1}{RC}\$ et

$\ c=\dfrac{E}{RC}$

Ainsi, en posant

$\tau=RC$ (constante de temps du circuit) on obtient :

$y(t)=u_{_{C}}(t)=E+k\mathrm{e}^{-\tfrac{t}{\tau}}\;,\quad k\text{ constante}$

Or, à

$t=0\;,\ u_{_{C}}=0$ donc,

$E+k\mathrm{e}^{0}=0\$ c'est-à-dire ;

$k=-E$

D'où,

$u_{_{C}}(t)=E\left(1-\mathrm{e}^{-\tfrac{t}{\tau}}\right)$ avec

$E=u_{_{C\text{ max}}}$

Par conséquent,

$\boxed{u_{_{C}}(t)=u_{_{C\text{ max}}}\left(1-\mathrm{e}^{-\tfrac{t}{\tau}}\right)}$

Étude graphique

Considérons la courbe représentative de la fonction

$u_{_{C}}(t)$ ci-dessous.

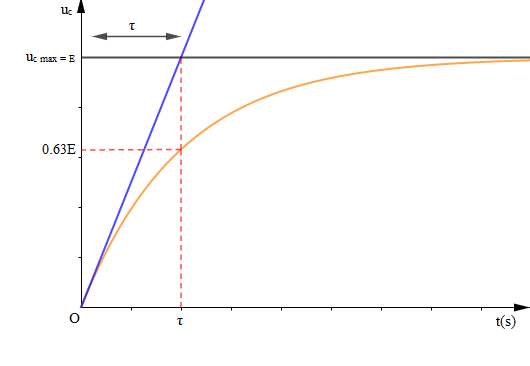
Soit

$\tau=RC$ la constante de temps du circuit. C'est un indicateur qui nous informe, en ordre de grandeur, sur la durée de charge du condensateur.

Détermination graphique de

$\tau$

Pour

$t=\tau$ , on a

$u_{_{C}}(t)=E\left(1-\mathrm{e}^{-1}\right)=0.63E=0.63u_{_{C\text{ max}}}$

Aussi, la tangente à

$t=0$ coupe la droite d'équation

$y=E=u_{_{C\text{ max}}}$ en

$t=\tau.$

Remarque :

Le condensateur est considéré comme chargé au bout d'une durée

$t=5\tau.$

Par ailleurs, on peut aussi déterminer

$\tau$ directement par le calcul en effectuant le produit

$RC$ ou en utilisant la relation

$u_{_{C}}(t)=E\left(1-\mathrm{e}^{-\tfrac{t}{\tau}}\right).$

Expression de $i$

On sait que

$i(t)=C.\dfrac{\mathrm{d}u_{_{C}}}{\mathrm{d}t}$ avec

$u_{_{C}}(t)=E\left(1-\mathrm{e}^{-\tfrac{t}{\tau}}\right)$ donc, après dérivation de

$u_{_{C}}(t)$ par rapport à

$t$ , on obtient :

$\boxed{i(t)=\dfrac{E}{R}\mathrm{e}^{-\tfrac{t}{\tau}}=\dfrac{u_{_{C\text{ max}}}}{R}\mathrm{e}^{-\tfrac{t}{\tau}}}$

On remarque que

$i$ décroit exponentiellement vers 0.

En effet,

$t=0\;,\ i=\dfrac{E}{R}\$ et lorsque

$t$ tend vers l'infini,

$i(t)$ tend vers 0.

Ainsi, lors de la charge d'un condensateur le courant décroit et s'annule à la fin de la charge.

Remarque :

La charge d'un condensateur n'est pas instantanée, c'est un phénomène transitoire.

En effet, le régime transitoire correspond au temps de charge

$t=5\tau$ du condensateur, et une fois celui-ci chargé on passe en régime permanent. Ce qui fait que l'intensité du courant dans le circuit est quasiment nulle.

III. Décharge d'un condensateur dans un conducteur ohmique

Considérons le montage ci-dessous

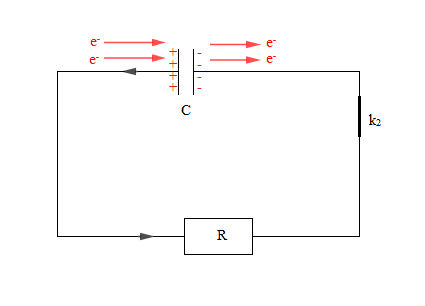
Lors de la décharge les électrons se déplacent dans le sens inverse du sens de leur déplacement pendant la charge. Ils quittent alors l'armature

$B$ pour arriver à l'armature

$A.$ Et le courant circule dans le sens contraire au sens de déplacement des électrons.

Ainsi,

$i<0\;,\ q$ diminue et

$\dfrac{\mathrm{d}q}{\mathrm{d}t}<0$

Équation différentielle

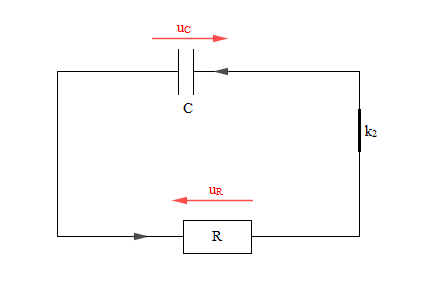
L'interrupteur

$k_{2}$ étant fermé, la décharge du condensateur s'effectue alors à travers le résistor

$R.$

La loi des mailles permet d'écrire :

$u_{_{C}}+u_{_{R}}=0\quad(1)$

Or, d'après la loi d'Ohm :

$u_{_{R}}=R.i\quad(2)$

Comme

$i(t)=C.\dfrac{\mathrm{d}u_{_{C}}}{\mathrm{d}t}$ alors, en remplaçant successivement

$i(t)$ dans l'équation (2) puis

$u_{_{R}}$ dans l'équation (1), on obtient :

$\boxed{RC.\dfrac{\mathrm{d}u_{_{C}}}{\mathrm{d}t}+u_{_{C}}=0}$

Cette équation différentielle d'ordre 1 à coefficients constants en

$u_{_{C}}$ peut encore s'écrire :

$\boxed{\dfrac{\mathrm{d}u_{_{C}}}{\mathrm{d}t}+\dfrac{u_{_{C}}}{RC}=0}$

D'après le cours de mathématiques, la solution est donnée par :

$\boxed{u_{_{C}}(t)=u_{_{C\text{ max}}}\mathrm{e}^{-\tfrac{t}{\tau}}}$

En supposant qu'à l'instant

$t=0\;,\ u_{_{C_{0}}}=u_{_{C\text{ max}}}=E$

Expression de $i$

Comme

$i(t)=C.\dfrac{\mathrm{d}u_{_{C}}}{\mathrm{d}t}$ avec

$u_{_{C}}(t)=E\mathrm{e}^{-\tfrac{t}{\tau}}$ alors,

$\boxed{i(t)=-\dfrac{E}{R}\mathrm{e}^{-\tfrac{t}{\tau}}=-\dfrac{u_{_{C\text{ max}}}}{R}\mathrm{e}^{-\tfrac{t}{\tau}}}$

On constate que

$i$ croit exponentiellement vers 0.

$t=0\;,\ i=-\dfrac{E}{R}=-\dfrac{u_{_{C\text{ max}}}}{R}$ et lorsque

$t$ tend vers l'infini

$i(t)$ tend vers 0.

Remarque :

Le courant de la décharge d'un condensateur est négatif. Cela est du au fait qu'il circule dans le sens contraire du sens de la charge.

Étude graphique

Dans cette phase de décharge on peut aussi déterminer graphiquement

$\tau.$

Considérons la courbe représentative de la fonction

$u_{_{C}}(t)$ ci-dessous.

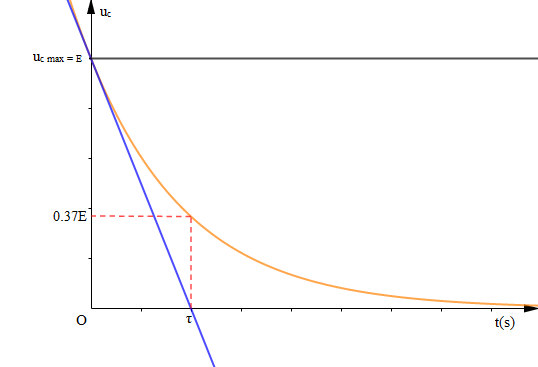
Pour

$t=\tau$ , on a

$u_{_{C}}(t)=E\mathrm{e}^{-1}=0.37E=0.37u_{_{C\text{ max}}}$

Par ailleurs, la tangente à

$t=0$ coupe l'axe des abscisses en

$t=\tau.$

IV. Énergie d'un condensateur

Lors de la charge, un condensateur emmagasine de l'énergie qu'il va, par la suite, restituer lors de la décharge.

Cette énergie est donnée par la relation :

$\boxed{E_{_{\text{élec}}}=\dfrac{1}{2}Cu_{_{C}}^{2}=\dfrac{1}{2}qu_{_{C}}=\dfrac{q^{2}}{2C}}$

Auteur:

Diny Faye

Commentaires

Mbaye (non vérifié)

ven, 08/30/2024 - 11:31

Permalien

Fame

Ta bien expliqué épi les leçons sont faciles à comprendre

répondre

Anonyme (non vérifié)

lun, 02/17/2025 - 22:05

Permalien

bon leçon

répondre

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.

Vous êtes ici

Le dipôle (R, C) - Ts

Formulaire de recherche

I. Le condensateur

I.1. Définition

I.2. Capacité d'un condensateur

I.3. Association de condensateurs

I.3.1. Association en série

I.3.2. Association en parallèle

II. Charge d'un condensateur

Équation différentielle

Étude graphique

Expression de ii

III. Décharge d'un condensateur dans un conducteur ohmique

Équation différentielle

Expression de ii

Étude graphique

IV. Énergie d'un condensateur

Commentaires

Fame

bon leçon

Ajouter un commentaire

Plain text

Expression de $i$

Expression de $i$