La résistance $R_{e}$ est la résistance équivalente à l'association des résistances $R_{1}$ et $R_{2}$.

Compléter le tableau ci-contre en indiquant les valeurs manquantes et/ou le type d'association.

$$\begin{array}{|c|c|c|c|}\hline R_{1}&R_{2}&R_{e}&\text{Types} \\ (\text{en }\Omega)&(\text{en }\Omega)&(\text{en }\Omega)&\text{d'associations} \\ \hline 680& &1500& \\ \hline &68&25& \\ \hline 470&33& &\text{Série} \\ \hline 51&46& &\text{parallèle} \\ \hline&56&28& \\ \hline \end{array}$$

Vous disposez de deux lots de résistances respectivement de $33\;\Omega$ et de $47\;\Omega$. Indiquez, en précisant le type d'association, le nombre de résistances de chaque que vous utilisez :

 

1) Une résistance de $100\;\Omega$

 

2) Une résistance de $113\;\Omega$

 

3) Une résistance de $130\;\Omega$

Trouver la résistance du conducteur équivalent à l'association :

 

1) en série de deux conducteurs de résistances respectives $22\;\Omega$ et $33\;\Omega$.

 

2) en parallèle des deux conducteurs de résistances respectives $22\;\Omega$ et $33\;\Omega$.

Vous disposez d'un ensemble de conducteurs identiques de résistance $33\;\Omega$ chacune. Comment les associer pour que la résistance du groupement obtenu soit de $11\;\Omega$.

Une lampe marquée $4.5\;v$ ; $\ 0.2\;A$ est montée en parallèle avec un conducteur de résistance $R_{1}=27\;\Omega$.

 

1) Calculer la résistance $R_{2}$ du fil chauffant de cette lampe.

 

2) Trouver la résistance équivalente à cette association.

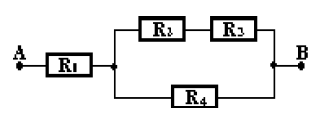
Soit le dipôle $AB$ constitué de conducteurs groupés comme indiqué dans le schéma suivant.

Trouver la résistance équivalente du dipôle $AB$ ainsi obtenu sachant que
$$R_{1}=10\;\Omega\;;\  R_{2}=20\;\Omega\;;\ R_{3}=6\;\Omega\text{ et }R_{4}=9\;\Omega$$

 

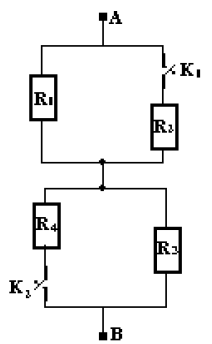
Des résistors de résistances respectives $R_{1}=12\;\Omega\;;\ R_{2}=R_{4}=6\;\Omega\text{ et }R_{3}=3\;\Omega$ sont groupés entre $A$ et $B$ comme indiqué par le schéma.

 

1) Trouver la résistance du dipôle $AB$ ainsi constitué.

 

2) A ce dipôle, on applique une tension de $6\;V$, déterminer l'intensité du courant débité par le générateur dans chacun des cas suivants.

 

a) Les interrupteurs $K_{1}$ et $K_{2}$ fermés

 

b) L'interrupteur $K_{1}$ fermé et l'interrupteur $K_{2}$ ouvert.

 

c) l'interrupteur $K_{1}$ ouvert et L'interrupteur $K_{2}$ fermé

 

d) Les interrupteurs $K_{1}$ et $K_{2}$ ouverts.

 

3) Calculer les intensités $I_{1}\;;\ I_{2}\;;\ I_{3}\text{ et }I_{4}$ pour $K_{1}$ et $K_{2}$ fermés.

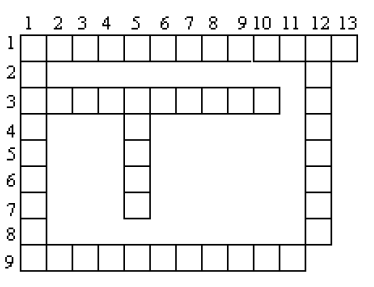
Donner les mots permettant de remplir la grille de mo ci-contre

 

Horizontalement

 

1) Placé aux bornes d'un générateur, il donne une tension variable.

 

3) Elle caractérise tout conducteur électrique.

 

9) Qualifie une résistance pouvant remplacer d'autres résistances

 

Verticalement

 

1) Se dit aussi d'un appareil placé en dérivation

 

5) Ainsi montés, les appareils sont traversés par le même courant.

 

12) Il est une résistance variable ; il fait varier l'intensité du courant