Vous êtes ici

Bases de la dynamique - Ts

Classe:

Terminale

La dynamique est l'étude des rapports entre les mouvements et les forces qui les engendrent.

I. Rappels

I.1. Vecteur quantité de mouvement

Considérons un solide de masse $m$, de centre d'inertie $G$, animé d'un mouvement de vecteur vitesse $\vec{v}_{_{G}}$, dans un référentiel $\mathcal{R}.$

On appelle vecteur quantité de mouvement par rapport au référentiel $\mathcal{R}$, le vecteur $\vec{p}$ défini par : $$\boxed{\vec{p}=m\vec{v}_{_{G}}\quad\text{en }\ (kg.m.s^{-1})}$$

I.2. Point matériel isolé ou pseudo-isolé

$-\ \ $ Un point matériel qui n'est soumis à aucune force extérieure est dit isolé.

$-\ \ $ Un point matériel est dit pseudo-isolé lorsque la somme des forces extérieures agissant sur lui s'annule. $$\sum \vec{F}_{\text{ext}}=\vec{0}$$

I.3. Référentiel galiléen

Un référentiel galiléen est un référentiel dans lequel un point matériel isolé ou pseudo-isolé est en mouvement rectiligne uniforme, s'il n'est pas au repos.

II. Relation fondamentale de la dynamique

Il faudra tout d'abord noter que les principes de la dynamique ne s'appliquent que dans un référentiel galiléen.

II.1. Énoncé

Dans un référentiel galiléen, la somme des forces extérieures appliquées à un solide est égale à la dérivée par rapport au temps du vecteur quantité de mouvement de ce solide. $$\boxed{\sum \vec{F}_{\text{ext}}=\dfrac{\mathrm{d}\vec{p}}{\mathrm{d}t}}$$

II.2. Les lois de Newton ou principes de la dynamique

II.2.1. Théorème du centre d'inertie (T.C.I) ou principe fondamental de la dynamique (P.F.D) (2e loi de Newton)

Dans un référentiel galiléen, si la somme des forces extérieures appliquées à un solide de masse $m$ ne s'annule pas $(\sum \vec{F}_{\text{ext}}\neq\vec{0})$ alors, centre d'inertie $G$ sera animé d'un mouvement varié d'accélération $\vec{a}_{_{G}}$ vérifiant : $$\boxed{\sum \vec{F}_{\text{ext}}=m\vec{a}_{_{G}}}$$

En effet,

$\begin{array}{rcl}\sum \vec{F}_{\text{ext}}&=&\dfrac{\mathrm{d}\vec{p}}{\mathrm{d}t}\quad\text{or }\ \vec{p}=m\vec{v}_{_{G}}\\ \\&=&\dfrac{\mathrm{d}(m\vec{v}_{_{G}})}{\mathrm{d}t}\quad m\ \text{ étant constante}\\ \\&=&m\dfrac{\mathrm{d}\vec{v}_{_{G}}}{\mathrm{d}t}\quad\text{or }\ \dfrac{\mathrm{d}\vec{v}_{_{G}}}{\mathrm{d}t}=\vec{a}_{_{G}}\\ \\&=&m\vec{a}_{_{G}}\end{array}$

D'où, $\sum \vec{F}_{\text{ext}}=m\vec{a}_{_{G}}$

II.2.2. Principe d'inertie (1e loi de Newton)

Dans un référentiel galiléen, le centre d'inertie $G$ d'un solide isolé ou pseudo-isolé est soit animé d'un mouvement rectiligne uniforme de vecteur vitesse $\vec{v}_{_{G}}$, soit au repos. On a alors : $$\boxed{\sum \vec{F}_{\text{ext}}=\vec{0}}$$

En effet, d'après la seconde loi de Newton, on a : $\sum \vec{F}_{\text{ext}}=m\vec{a}_{_{G}}$

Or, $\sum \vec{F}_{\text{ext}}=\vec{0}$ donc, $\vec{a}_{_{G}}=\vec{0}$

D'où, $\vec{v}_{_{G}}=\text{cst}\neq 0$ ; ce qui est caractéristique d'un mouvement rectiligne uniforme.

Et dans le cas où $\vec{v}_{_{G}}=\vec{0}$, le solide est alors au repos.

II.2.3. Principe des actions réciproques ou principe de l'action et de la réaction (3e loi de Newton)

Considérons deux points matériels $A$ et $B.$

Si $A$ exerce sur $B$ une force $\vec{F}_{_{A\rightarrow B}}$ appelée force d'action alors, $B$ exerce aussi sur $A$ une force $\vec{F}_{_{B\rightarrow A}}$ appelée force de réaction telles que : $$\boxed{\vec{F}_{_{A\rightarrow B}}=-\vec{F}_{_{B\rightarrow A}}}$$

III. Théorème de l'accélération angulaire

Considérons un anneau de rayon $R$ et de masse $m$ en mouvement de rotation autour d'un axe $\Delta$ sous l'action d'une force $\vec{F}.$

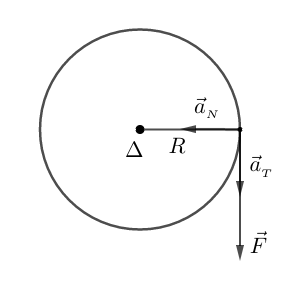
Le théorème du centre d'inertie permet d'écrire : $$\vec{F}=m\vec{a}$$

En projetant cette relation dans la base de Frenet on obtient :

$$\left\lbrace\begin{array}{rcl} F&=&ma_{_{T}}\\0&=&ma_{_{N}}\end{array}\right.$$

Donc, $F=ma_{_{T}}\quad\text{or }\ a_{_{T}}=\dfrac{\mathrm{d}v}{\mathrm{d}t}$

Ainsi, $F=m\dfrac{\mathrm{d}v}{\mathrm{d}t}$

Par suite,

$\begin{array}{rcl} FR&=&mR\dfrac{\mathrm{d}v}{\mathrm{d}t}\quad\text{or }\ v=R\dot{\theta}\\ \\&=&mR\dfrac{\mathrm{d}(R\dot{\theta})}{\mathrm{d}t}\\ \\&=&mR^{2}\ddot{\theta}\quad\text{or }\ FR=\mathcal{M}_{_{/\Delta}}^{\vec{F}}\;\ \text{ et }\;\ mR^{2}=J_{_{\Delta}}\\ \\ \mathcal{M}_{_{/\Delta}}^{\vec{F}}&=&J_{_{\Delta}}.\ddot{\theta}\end{array}$

Et pour plusieurs forces appliquées à ce solide on obtient : $$\boxed{\sum\mathcal{M}_{_{/\Delta}}^{\vec{F}}=J_{_{\Delta}}.\ddot{\theta}}$$

La somme algébrique des moments des différentes forces qui s'appliquent à un solide en mouvement de rotation autour d'un axe $\Delta$ est égale au produit du moment d'inertie de ce solide par l'accélération angulaire.

Moments d'inertie de quelques solides

$\centerdot\ \ $ Disque ou cylindre plein de masse $m$ et de rayon $R\;;\ J_{_{\Delta}}=\dfrac{1}{2}mR^{2}$

$\centerdot\ \ $ Sphère pleine de masse $m$ et de rayon $R\;;\ J_{_{\Delta}}=\dfrac{2}{5}mR^{2}$

$\centerdot\ \ $ Cylindre creux de masse $m$ et de rayon $R\;;\ J_{_{\Delta}}=mR^{2}$

$\centerdot\ \ $ Tige de masse $m$ et de longueur $\ell\;;\ J_{_{\Delta}}=\dfrac{1}{12}m\ell^{2}$

Théorème de Huygens

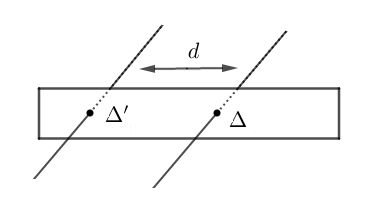
Considérons une tige de masse $m$ et d'axe $\Delta$ et soit $\Delta'$ un autre axe tel que $\text{dist}(\Delta\;;\ \Delta')=d.$ Le moment d'inertie du solide par rapport à $\Delta'$ est alors donné par : $$\boxed{J_{_{\Delta'}}=J_{_{\Delta}}+md^{2}}$$

IV. Méthode d'application

Pour une meilleure application de la relation fondamentale de la dynamique dans des exercices ou problèmes de dynamique, nous adoptons la démarche suivante :

$\centerdot\ \ $ Définir ou préciser le système à étudier.

$\centerdot\ \ $ Choisir un référentiel galiléen.

$\centerdot\ \ $ Faire le bilan des forces extérieures appliquées au système.

$\centerdot\ \ $ Appliquer un des principes de la relation fondamentale de la dynamique.

$\centerdot\ \ $ Choisir un repère de projection.

$\centerdot\ \ $ Projeter la relation fondamentale de la dynamique sur les axes de ce repère.

$\centerdot\ \ $ Résoudre les équations obtenues en tenant compte des conditions initiales.

Remarque

Il faut aussi tenir compte de l'application des théorèmes de l'énergie cinétique et de l'accélération angulaire qui intervient assez souvent, dans la résolution de certaines questions.

Auteur:

Diny Faye