Vous êtes ici

Énergie cinétique - 1er s

Classe:

Première

I. Notion d'énergie cinétique

1. Observation

Un mur peut être détruit par une automobile animée d'une grande vitesse. L'automobile animée d'une grande vitesse produit du travail, elle possède de l'énergie cinétique. Cette énergie est due au mouvement.

2. Définition

On appelle énergie cinétique l'énergie que possède un corps du fait de sa vitesse (ou de son mouvement)

3. Expression de l'énergie cinétique

3.1. Expression de l'énergie cinétique d'un point matériel

Un point matériel est une particule dont les dimensions sont suffisamment petites pour qu'on puisse l'assimilé à un point. Si le point $A$ de masse $m$ se déplace à la vitesse $v$, son Énergie cinétique est donné par la formule.

$$E_{c}=\dfrac{1}{2}mv^{2}$$

$V$ en $m\cdot s^{-1}$ ;

$m$ en $kg$ et

$E_{c}$ en $J$

3.2. Énergie cinétique d'un corps solide en translation

Un solide $(s)$ est en translation, si à chaque instant tous les points du solide ont le même vecteur vitesse

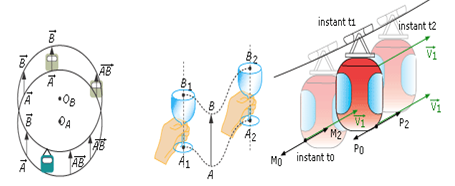
$\overrightarrow{v_{1}}=\overrightarrow{v_{2}}=\overrightarrow{v_{3}}=\overrightarrow{v_{4}}\ldots\ldots\overrightarrow{v_{n}}=\overrightarrow{v}$

L'énergie cinétique total est la somme des énergies cinétiques des points matériels tels que :

$$E_{c}=\sum_{i=1}^{n}E_{c_{1}}=\sum_{i=1}^{n}\dfrac{1}{2}m_{i}v_{i}^{2}=\sum_{i=1}^{n}\dfrac{1}{2}m_{i}v^{2}=\dfrac{1}{2}v^{2}\sum_{i=1}^{n}m_{i}$$

Or $\sum_{i=1}^{n}m_{i}$ représente la masse totale $(m)$ du système. L'énergie cinétique de masse $(m)$ s'écrit donc :

$$E_{c}=\dfrac{1}{2}mv^{2}$$

3.3. Énergie cinétique d'un solide en rotation

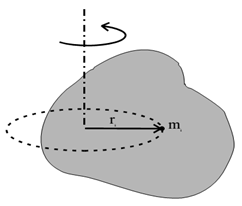
Un corps rigide quelconque tourne autour d'un axe de rotation dont la position et l'orientation restent fixes.

Le corps est constitué de particules ponctuelles de masse mi situées à une distance ride l'axe de rotation. L'énergie cinétique d'une de ces particules est : $E_{c_{i}}=\dfrac{1}{2}\cdot m_{i}\cdot v_{i}^{2}$

avec $v_{i}^{2}=r_{i}\cdot w$ ; $w$ la vitesse angulaire

$$E_{c_{i}}=\dfrac{1}{2}\cdot m_{i}\cdot r_{i}^{2}\cdot w$$

L'énergie cinétique totale de rotation est :

$$E_{c}=\sum\,E_{c_{i}}=\sum\dfrac{1}{2}\cdot m_{i}\cdot r_{i}^{2}\cdot w^{2}=\dfrac{1}{2}\cdot w^{2}\cdot\sum\,m_{i}\cdot r_{i}^{2}$$

L'énergie cinétique d'un solide en mouvement de rotation peut s'écrire sous la forme :

$E_{c}=\dfrac{1}{2}J_{\Delta}\omega^{2}$ ; avec $\omega$ en $rad\cdot s^{-1}$

avec $J_{\Delta}=\sum\,m_{i}\cdot r_{i}^{2}$

La grandeur $J_{\Delta}$ est appelée le moment d'inertie du corps par rapport à l'axe de rotation $(\Delta)$ en kilogrammes carrés $(kg\cdot m^{2})$

Moments d'inertie de quelques solides usuels

3.4. Énergie cinétique d'un solide animé d'un mouvement quelconque

Dans le cas où le solide est animé d'un mouvement complexe (translation, rotation, pivotement) combinés, on admet que son énergie cinétique est la somme des deux :

$\blacktriangleright\ $Une énergie cinétique de translation de centre de gravité ou toute la masse serait concentrée

$\blacktriangleright\ $Une énergie cinétique de rotation autour de l'axe passant chaque instant par le centre de gravité

$$E_{c}=\dfrac{1}{2}mv^{2}+\dfrac{1}{2}J_{\Delta}\omega^{2}$$

II. Théorème de l'énergie cinétique

1. Rappel

La variation d'une grandeur physique $(G)$ associée à un système entre l'instant initial $(i)$ et l'instant final $(f)$ est notée

$$\Delta G=G_{j}-G_{i}$$

2. Énoncé du théorème de l'énergie cinétique

La variation de l'énergie cinétique d'un système indéformable ou solide entre deux instants est égale à la somme algébrique des travaux de toutes les formes extérieures agissant sur le système entre les instants.

$$\Delta E_{c}=\sum_{i=1}^{n}W_{F_{\text{extérieur}}}$$

Remarque :

Avant d'appliquer ce théorème, il faut :

$\blacktriangleright\ $Délimiter précisément le système

$\blacktriangleright\ $Définir les 2 états entre lesquels on étudie le système

$\blacktriangleright\ $Déterminer toutes les forces extérieures qui agissent sur le système entre ces deux états

3. Conclusion

Le théorème de l'énergie cinétique montre que le travail est un transfert d'énergie entre l'extérieur et le système lorsque ce dernier passe d'un état à un autre. Chaque état peut être caractérisé par une valeur de l'énergie cinétique et le travail de toutes les forces extérieures correspond à la variation de la fonction de l'énergie cinétique. Le travail ne peut pas caractériser l'état d'un système. C'est un transfert d'énergie qui n'apparait lorsque le système passe d'un état à un autre.

Exercice d'application

Un polit de masse $m=4.5\,kg$ est lancée du point $O$ vers le haut, avec une vitesse initiale $V_{O}=4.2\,m\cdot s^{-1}$ suivant la ligne de plus grande pente d'un plan incliné de $\alpha=12^{\circ}$ par rapport au plan horizontal.

1. On suppose que les frottements sont négligeables.

Quelle est la vitesse $V_{1}$ du palet lorsqu'il a parcouru la distance $d_{1}=OA=2.7\,m$

2. Au bout de quelle distance $d_{2}$ égale à $O_{3}.$

La vitesse du palet s'annule-t-elle ?

3. L'obsevation montre que la vitesse du palet s'annule en fait au bout de du distance $d=OC=4.05\,m.$

Quelle est la valeur $f$ de la force de frottement $f$ supposé constante exercée par le plan sur le palet $g=10N/Kg$

Résolution :

2. La vitesse $V_{1}$ du palet

Système étudié : le palet

Référentiel d'étude : référentiel terrestre supposé galiléen

Bilan des forces extérieures appliquées au palet : $\overrightarrow{P}\;,\ \overrightarrow{R}$

Le théorème cinétique appliqué au palet s'écrit :

\begin{eqnarray} \Delta E_{c} &=&\sum W_{\overrightarrow{F}\text{ext}}\nonumber\\\\\Rightarrow E_{c_{1}}- E_{c_{0}} &=& W_{OA}\left(\overrightarrow{P}\right)+W_{OA}\left(\overrightarrow{R}\right)\nonumber\\\\\Rightarrow\dfrac{1}{2}mv_{1}^{2}--\dfrac{1}{2}mv_{0}^{2} &=&-mgd_{1}\sin\theta+0\nonumber\\\\\Rightarrow v_{1}^{2} &=& v_{0}^{2}-2gd_{1}\sin\theta\nonumber\\\\\Rightarrow v_{1} &=& \sqrt{v_{0}^{2}-2gd_{1}\sin\theta}\nonumber\\\\ &=&\sqrt{4.2^{2}-2\times 10\times 2.7\times\sin 12^{\circ}}\nonumber\\\\\Rightarrow v_{1} &=& 2.5m\cdot s^{-1} \end{eqnarray}

2. La distance $d_{2}$

Par analogie :

\begin{eqnarray} v_{2}^{2} &=& v_{0}^{2}-2gd_{2} \sin\theta\quad\text{or }v_{2}^{2} &=& 0m\cdot s^{-1}\nonumber\\\\Rightarrow\;d_{2}&=&\dfrac{v_{0}^{2}}{2g\sin\theta}\nonumber\\\\ &=&\dfrac{2\cdot4^{2}}{2\times10\times\sin 12^{\circ}}\nonumber\\\\\Rightarrow\;d_{2}&=&4.2m \end{eqnarray}

3. La valeur de $f$

Le théorème de l'énergie cinétique compte tenu de la force de frottement $f$ s'écrit :

\begin{eqnarray} E_{c_{3}}-E_{c_{0}} &=&W_{OC}\left(\overrightarrow{P}\right)+W_{OC}\left(\overrightarrow{R}\right)+W_{OC}\left(\overrightarrow{f}\right)\nonumber\\\\\Rightarrow 0-\dfrac{1}{2}mv_{0}^{2}&=& -mgd\sin\theta-fd \nonumber\\\\\Rightarrow\;f &=&m\left(\dfrac{v_{0}^{2}}{2d}-g\sin\theta\right)\nonumber\\\\\Rightarrow\;f &=&4.5\left(\dfrac{4.2^{2}}{2\times4.05}-10\times\sin 12^{\circ}\right)\nonumber\\\\\Rightarrow f &=& 0.44N \end{eqnarray}

Auteur:

Sidy Mouhamed Ndiaye