1. Continuité d’une fonction
1.1. Notion de continuité
Définition :
On considère une fonction $f\text{ définie sur un intervalle }I.$
On dit que la fonction $f$ est continue sur $I$ si la courbe représentant la fonction $f$ « se trace d'un trait continue ». (Sans lever le crayon)
Exemples :
$\bullet$ La fonction racine carrée est continue sur $]0\;,\ +\infty[$
$\bullet$ La fonction inverse est continue sur $]0\;,\ +\infty[$ mais n'est pas continue sur $[-1\;;\ 1]$
1.2. Fonctions usuelles
Propriétés :
$\bullet$ Les fonctions $x\mapsto x^{n}\;,\text{ où }n$ est un entier naturel, sont continues sur $\mathbb{R}$
$\bullet$ Toute fonction polynôme est continue sur $\mathbb{R}.$
$\bullet$ Les fonctions $x\mapsto\dfrac{1}{x^{n}}\;,\text{ où }n$ est un entier naturel, sont continues sur $\mathbb{R}\text{ et sur }I.$
$\bullet$ Toute fonction rationnelle est continue sur chaque intervalle de son ensemble de définition.
Exemples :
$\bullet$ La fonction $f$ définie sur $\mathbb{R}\text{ par }f(x)=x^{2}-2x^{3}+x-7$ est continue sur $\mathbb{R}.$
$\bullet$ La fonction $g$ définie par $g(x)=\dfrac{4x-1}{x-2}$ est continue sur $\mathbb{R}\setminus\{2\}$
Proposition :
Si $f\text{ et }g$ sont continués en $a$ alors, $f+g\;,\ f−g\;,\ f\times g$, sont continués en $a.$
Il en est de même $(\text{si }f(a)\text{ non nul})$ et $(\text{si }g(a)\text{ non nul}).$
Pour les économistes, la notion de continuité sert à garantir l'existence de solutions à des équations non linéaires.
En effet, les théories économiques se formalisent souvent par des systèmes de plusieurs équations à plusieurs inconnues (a priori il y a autant d'équations que d'inconnues).
Il est rare que ces systèmes soient linéaires, ce qui rend leur résolution explicite difficile voire impossible.
Or il existe néanmoins des outils mathématiques pour caractériser ces solutions.
La première chose à caractériser est de savoir si une solution existe.
1.3. Théorème de la valeur intermédiaire
Définition :
Une fonction est strictement monotone sur un intervalle $I$ si elle est strictement croissante (ou strictement décroissante) sur cet intervalle.
Théorème (dit de la valeur intermédiaire) :
Si $f$ est une fonction continue et strictement monotone sur un intervalle $[a\;;\ b]$ alors pour tout réel $k$ compris entre $f(a)\text{ et }f(b)$ il existe un unique réel $c$ de l'intervalle $[a\;;\ b]\text{ tel que }f(c)=k.$
Exemple :
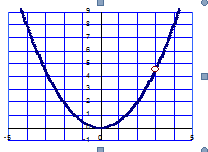
La courbe représentative de la fonction f est une parabole.Le nombre réel $4$ est une valeur intermédiaire entre $f(0)\text{ et }f(4)$ et la fonction $f$ est strictement croissante sur $[0\;;\ 4]$ d'après le théorème des valeurs intermédiaires, il existe un unique réel $c\text{ vérifiant }f(c)=4.$
2. Limites
La notion de limite d'une fonction est assez intuitive.
Mais elle est beaucoup plus difficile à formaliser mathématiquement.
On veut donner un sens à la phrase :
$$f(x)\text{ tend vers }l\text{ quand }x\text{ tend vers }a.$$
On entend par là que $f(x)$ se rapproche de $l$ “ autant qu'on le souhaite ”, pourvu que $x$ soit “ suffisamment proche ” de $a.$
Cela nous conduit à la définition suivante :
2.1 Définition :
On dit que $f(x)$ admet $l$ pour limite quand $x$ tend vers $a$ et on note $\lim_{x \to a}f(x)\leftrightarrow \forall\;\epsilon >0\;,\ \exists\;d>0$ tel que : $$x\text{ vérifiant }|x−a|\leq d\;,\text{ on ait }|f(x)−l|\leq \epsilon$$
ou encore
$\forall\;\epsilon >0\;,\ \exists d>0\text{ tel que pour tout }x\,\in\,[a−d\;,\ a+d]\;,\text{ on ait }|f(x)−l|\leq \epsilon.$
2.2 Limites usuelles
$$\begin{array}{|c|c|c|} \hline \text{Limite infinie à l'infinie}&\text{Limite nulle à l'infinie}&\text{Limite infinie en 0}\\ \hline \lim_{x \to +\infty}x^{2}=+\infty&\lim_{x \to +\infty}\dfrac{1}{x}=0&\lim_{\substack{x \to 0 \\ x>0}}\dfrac{1}{x}=+\infty\\ \lim_{x \to +\infty}x^{3}=+\infty&\lim_{x \to +\infty}\dfrac{1}{x^{2}}=0&\lim_{\substack{x \to 0 \\ x>0}}\dfrac{1}{x^{2}}=+\infty\\ \lim_{x \to +\infty}\sqrt{x}=+\infty&\lim_{x \to +\infty}\dfrac{1}{\sqrt{x}}=0&\lim_{\substack{x \to 0 \\ x<0}}\dfrac{1}{x}=-\infty\\ \lim_{x \to -\infty}x^{2}=+\infty&\lim_{x \to -\infty}\dfrac{1}{x}=0&\lim_{\substack{x \to 0 \\ x<0}}\dfrac{1}{x^{2}} =-\infty\\ \lim_{x \to -\infty}x^{3}=+\infty&\lim_{x \to -\infty}\dfrac{1}{x^{2}}=0& \\ \hline \end{array}$$
3. Limites par opérations
Dans tout ce qui suit, $\alpha$ désigne, soit un nombre réel, soit $+\infty$, soit $-\infty$ et $L\text{ et }L'$ sont des nombres réels.
3.1. Limite d’une somme
Définition :
$f\text{ et }g$ étant deux fonctions définies sur le même intervalle $I$, leur somme $f+g$ est la fonction définie sur $I$ par
Théorème :
$$\begin{array}{|c|c|c|c|c|c|c|} \hline \text{Si }\lim_{x \to a}f(x)=&L&L&L&+\infty&+\infty&-\infty\\ \hline\text{et }\lim_{x \to a}g(x)=&L'&+\infty&-\infty&+\infty&-\infty&+\infty\\ \hline\text{alors }\lim_{x \to a}(f+g)(x)&L+L'&+\infty&-\infty&+\infty&-\infty&?\\ \hline \end{array}$$
Exemples :
$f\ :\ x\mapsto(x^{2}+\dfrac{1}{x})\text{ si }x\to-\infty$;
$g\ :\ x\mapsto(x^{2}+x)\text{ si }x\to-\infty$ (indéterminé)
3.2. Limite d’un produit
Définition :
$f\text{ et }g$ étant deux fonctions définies sur le même intervalle $I$, leur produit $f\,g$ est la fonction définie sur $I\text{ par }f\times g(x)=f(x)\times g(x) $
Théorème :
$$\begin{array}{|c|c|c|c|c|} \hline \text{Si }\lim_{x\to \alpha}f(x)=&L&L\text{ non nul}&0&+\infty\text{ ou }-\infty\\ \hline \text{et }\lim_{x\to \alpha}g(x)=&L'&+\infty\text{ ou }-\infty&+\infty\text{ ou }-\infty&+\infty\text{ ou }-\infty&\\ \hline\text{alors }\lim_{x\to \alpha}(fg)(x)=&L\times L'&\pm\infty\text{ règle des signes}&?&\pm\infty\\ \hline \end{array}$$
$h\ :\ x\mapsto 2x^{3}\left(\dfrac{1}{x}-3\right)\text{ si }x\to +\infty$
$k\ :\ x\mapsto 2x^{2}(x^{2}-1)\text{ si }x\to -\infty$ (indéterminé)
3.3. Limite d’un quotient
$$\begin{array}{|c|c|c|c|c|c|c|} \hline \text{Si }\lim_{x\to \alpha}f(x)=&L&L\text{ non nul}&L&\pm \infty&0&\pm\infty\\ \hline \text{Et }\lim_{x\to \alpha}g(x)=&L'\text{ non nul}&0&\pm\infty&L'&0&\pm\infty\\ \hline \text{alors }\lim_{x\to \alpha}\left(\dfrac{f}{g}\right)(x)=&\dfrac{L}{L'}&\pm \infty\text{ Règle des signes}&0&\pm\infty\text{ Règle des signes}&?&?\\ \hline \end{array}$$
Exemple :
$l\ :\ x\mapsto\dfrac{x-3}{1-x^{2}}\text{ si }x\to 1\text{ avec }x>1$
$p\ :\ x\mapsto\dfrac{1+4x^{2}}{x^{2}-9}\text{ si }x\to +\infty$
3.4. Lever une indétermination.
Méthodes :
Dans le cas où les théorèmes par opérations ne s'appliquent pas, on détermine une limite à l'infini d'une fonction polynôme ou rationnelle en transformant l'expression : dans chaque polynôme, on met en facteur la plus grande puissance de $x$ et on simplifie pour appliquer les théorèmes.
Dans le cas d'une fonction rationnelle $\dfrac{P(x)}{Q(x)}$ , pour lever une indétermination du type « $\dfrac{0}{0}$ » en une valeur $a$, on pose $x=a+h$ et on étudie la limite en $0$ de la fonction de $h$ obtenue.
Exemples
$g\ :\ x\mapsto(x^{2}+x)\text{ si }x\to -\infty$
$k\ :\ x\mapsto\dfrac{2}{x^{2}}{x^{2}-1}\text{ si }x\to -\infty$
$p\ :\ x\mapsto\dfrac{1+4x^{2}}{x^{2}-9}\text{ si }x\to +\infty$
$t\ :\ x\mapsto\dfrac{2x^{2}-x-3}{6x^{2}+4x-2}\text{ si }x\to -1 $
Théorème :
-
La limite à l’infini d’un polynôme est égale à la limite de son monôme de plus haut degré :
$\lim_{x\to \infty} ax^{n}+bx^{n-1}+\cdots+c=\lim_{x\to \infty}ax^{n}$
-
La limite à l’infini d’une fonction rationnelle est égale à la limite du quotient des monômes de plus haut degré :
$\lim_{x\to \infty}\dfrac{ax^{n}+bx^{n-1}+\cdots+c}{\alpha x^{p}+\beta x^{p-1}+\cdots+\delta}=\lim_{x\to \infty}\dfrac{ax^{n}}{\alpha x^{p}}$
3.5. Asymptotes
Propriété :
Soit $c$ un nombre réel. Si $\lim_{x\to c}f(x)=+\infty\text{( ou }-\infty)$ alors la droite d'équation $x=c$ est une asymptote « verticale » à la courbe représentant la fonction $f$ au voisinage de $c$
Exemple :
Propriété :
Soit $b$ un nombre réel. Si $\lim_{x\to +\infty}f(x)=b\text{( ou }\lim_{x\to -\infty}f(x)=b)$ alors la droite d'équation $y=b$ est une asymptote « horizontale » à la courbe représentant la fonction $f$ au voisinage de $+\infty\text{( ou }-\infty.$
Remarque :
On peut démontrer que $\lim_{x\to +\infty}(f(x)-b)=0\quad (\lim_{x\to -\infty}(f(x)-b)=0$
Exemple :
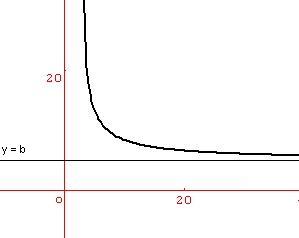
Propriété :
Soient $a\text{ et }b$ deux nombres réels.
Si $\lim_{x\to +\infty}(f(x)-(ax+b))=0$ alors la droite $\Delta$ d'équation $y=ax+b$ est une asymptote « oblique » à la courbe représentant la fonction $f$ au voisinage de $+\infty\text{( ou }-\infty).$
Exemple :
Corollaire :
Si la fonction $f$ peut s'écrire $f(x)=ax+b+\phi(x)$ avec $ \lim_{x\to \pm\infty} (\phi(x)=0$ alors la droite d'équation $y=ax+b$ est une asymptote « oblique » à la courbe représentant de la fonction $f$ au voisinage de $\pm\infty.$
Remarques :
Pour connaître la position relative d'une courbe et de son asymptote oblique, on étudie le signe de la différence $f(x)-(ax+b).$
Une courbe peut traverser son asymptote horizontale ou oblique, mais jamais une asymptote verticale.
3.5. Limites par comparaison
Théorème :
S'il existe un réel $A$ tel que pour tout $x\geq A\;,\ f(x)\geq g(x)\text{ et }\lim_{x\to +\infty}g(x)=+\infty\text{ alors }\lim_{x\to +\infty}f(x)=+\infty.$
Exemple :
Soit $f$ une fonction telle que pour tout $x\neq 0\;,\ f(x)\geq x^{2}+x-\dfrac{1}{x^{2}}$ , en déduire $\lim_{x\to +\infty}f(x).$
Théorème :
S'il existe un réel $A$ tel que pour tout $x\geq A\;,\ f(x)\leq g(x)\text{ et }\lim_{x\to +\infty}g(x)=-\infty\lim_{x\to +\infty}f(x)=-\infty$
Exemple :
Soit $f$ une fonction telle que pour tout $x\neq 2\;,\ f(x)\leq\dfrac{-2x^{3}+x-3}{2x^{2}-5}$ , en déduire $\lim_{x\to +\infty}f(x).$
Théorème : (dit des gendarmes)
$L$ désigne un nombre réel. S'il existe un réel $A$ tel que pour tout $x\geq A\;,\ u(x)\leq f(x)\leq v(x)\text{ et si }\lim_{x\to +\infty}u(x)=\lim_{x\to +\infty} v(x)=L\text{ alors }\lim_{x\to +\infty}f(x)=L$
Exemple :
Soit $f$ une fonction telle que pour tout $x\geq 3\;,\ \dfrac{-x+2}{x^{2}+3}\leq f(x)\leq\dfrac{3x+1}{x^{2}-8}\;,\text{ en déduire }\lim_{x\to +\infty}f(x)$
Remarque :
On dispose de théorèmes analogues quand $x$ tend vers $-\infty$ en remplaçant $x\geq A\text{ par }x\neq A$ ou quand $x$ tend vers un réel $a.$
Exemple :
Soit $k$ une fonction telle que pour tout $x\geq 0$,
$\dfrac{4x^{2}-4x+2}{x^{2}+1}\leq k(x)\leq\dfrac{4x^{2}+x+4}{x^{2}+2}\;,\text{ en déduire }\lim_{x\to +\infty}k(x)\text{ et }\lim_{x\to +0^{+}}k(x).$
3.6. Limite d’une fonction composée
Théorème :
$\alpha\;,\ m\text{ et }l\text{ désignent des nombres réels ou }+\infty\text{ ou }-\infty$
$\begin{array}{lcl}\lim_{x\to +\infty}u(x)&=&m\text{ et }\lim_{x\to +\infty}v(x)\\&=&l\text{ donc }\lim_{x\to \alpha}v\circ u(x)\\&=&ml\end{array}$
Exemple
Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x)=\sqrt{x^{2}+x+2}$ peut s'écrire sous la forme $v\circ u\text{ avec }u(x)=x^{2}+x+1\text{ et }v(x) =\sqrt{x}.$
$\begin{array}{lcl}\lim_{x\to -\infty}u(x)&=&+\infty\text{ et }\lim_{x\to +\infty}v(x)\\&=&+\infty\text{ donc }\lim_{x\to -\infty}f(x)\\&=&+\infty\end{array}$



Commentaires
Sène (non vérifié)
mar, 10/01/2019 - 18:30
Permalien
Pour un cours
Aliou Diallo (non vérifié)
mer, 07/22/2020 - 17:29
Permalien
Ce cours est formidable
Latif (non vérifié)
mar, 11/10/2020 - 12:52
Permalien
Incha'Allah
Anonyme (non vérifié)
ven, 07/19/2024 - 02:55
Permalien
Cool
Ajouter un commentaire