Statistique 3e
Classe:
Troisième
Introduction
La paternité du mot "statistique" est généralement attribuée à un professeur allemand du nom de G.Achenwaall qui l'aurait fait dériver du mot "staaskuarde" qui signifie "science des états".
La statistique est une branche des mathématiques dont les principes découlent à la fois d'un recueil de données d'observations concernant par exemple la connaissance des états ou des sociétés humaines et des méthodes de traitement et d'observation de ces données.
Aujourd'hui, l'exploitation des données statistiques se fait avec l'utilisation de certaines branches mathématiques mais notre étude elle, portera essentiellement sur les préliminaires à savoir ; le vocabulaire, les paramètres de position et les représentations graphiques.
I. Classement des données statistiques - Définitions
A la suite d'un recensement de la taille (en cm) des élèves de $3^{eme}$ de deux établissements différents, il a été décelé les tailles suivantes :
$\centerdot\ \ $ Taille des élèves de $3^{eme}$ du Collège Pie XII :
$$\begin{array}{|c|c|c|c|c|}\hline 166 & 145 & 150 & 150 & 166 \\ \hline 158 & 158 & 162 & 162 & 158 \\ \hline 165 & 162 & 154 & 158 & 160 \\ \hline 162 & 154 & 165 & 160 & 160 \\ \hline 158 & 154 & 158 & 160 & 165 \\ \hline\end{array}$$
$\centerdot\ \ $ Taille des élèves de $3^{eme}\;F$ du $CEM_{2}$ V. Ndiaye :
$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|}\hline 157 & 172 & 170 & 172 & 168 & 173 & 152 & 184 & 150 & 199 \\ \hline 162 & 160 & 185 & 166 & 188 & 175 & 173 & 168 & 148 & 154 \\ \hline 171 & 168 & 173 & 149 & 171 & 183 & 184 & 163 & 153 & 146 \\ \hline 170 & 173 & 166 & 168 & 169 & 182 & 185 & 163 & 152 & 161 \\ \hline 160 & 167 & 162 & 163 & 170 & 185 & 177 & 157 & 166 & 188\\ \hline\end{array}$$
Le recueil de ces données est sous la présentation d'une série statistique brute.
Pour faire une bonne étude statistique, on ordonne ces valeurs dans un tableau faisant apparaitre le nombre d'élèves pour chaque taille trouvée ou intervalle (classe) de taille considéré.
$\centerdot\ \ $ Tableau relatif aux élèves de $3^{eme}$ du Collège Pie XII
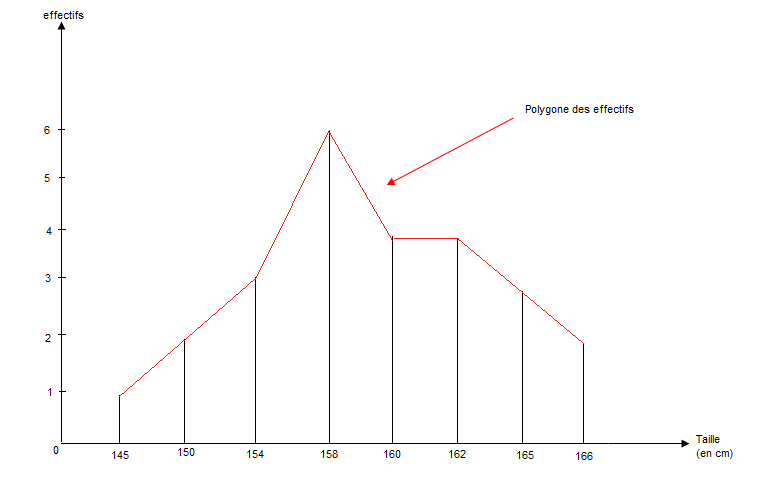
$$\begin{array}{|c|c|c|c|c|c|c|c|c|}\hline \text{Tailles (en }cm) & 145 & 150 & 154 & 158 & 160 & 162 & 165 & 166 \\ \hline\text{Effectifs} & 1 & 2 & 3 & 6 & 4 & 4 & 3 & 2 \\ \hline\end{array}$$
$\centerdot\ \ $ Tableau relatif aux élèves de $3^{eme}\;F$ du $CEM_{2}$ V. Ndiaye
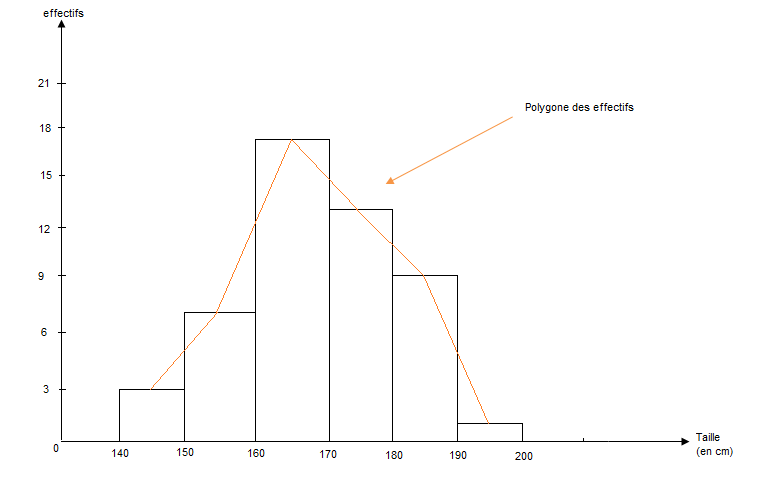
$$\begin{array}{|c|c|c|c|c|c|c|}\hline\text{Classe de tailles (en }cm) & [140\;;\ 150[ & [150\;;\ 160[ & [160\;;\ 170[ & [170\;;\ 180[ & [180\;;\ 190[ & [190\;;\ 200[ \\ \hline\text{Effectifs} & 3 & 7 & 17 & 13 & 9 & 1 \\ \hline\end{array}$$
$\centerdot\ \ $ Les tableaux ainsi présentés sont appelés des séries statistiques (ordonnées).
Dans le tableau relatif aux élèves de 3e du Collège Pie XII, c'est une série statistique permettant de déceler le nombre d'élèves pour chaque taille trouvée par contre, dans le deuxième tableau c'est une série statistique permettant de déceler le nombre d'élèves pour chaque intervalle (classe) de tailles considérées.
$\centerdot\ \ $ On appelle population d'une série statistique, l'ensemble sur lequel l'étude a eu à porter.
Dans le deuxième tableau la population ainsi étudiée trouve être les élèves de la $3^{eme}\;F$ du $CEM_{2}$ V. Ndiaye.
Chaque élève de la série statistique définit un individu dont un ensemble constituera un échantillon.
$\centerdot\ \ $ On appelle caractère d'une série statistique, une propriété commune à l'ensemble de la population étudiée. Dans le cas de notre étude, le caractère ainsi défini est la taille.
On distingue deux types de caractères :
$-\ $ caractère quantitatif : c'est un caractère mesurable (taille, poids, age, note, taux de croissance, distance...)
$-\ $ caractère qualitatif : c'est un caractère non mesurable (nationalité, ethnies, couleur, sport pratiqué...)
Toute valeur prise par un caractère est appelée une modalité ; dans le tableau relatif aux élèves de $3^{eme}$ du Collège Pie XII, on peut alors parler de la modalité 145, 150, 154....
Quand la modalité peut prendre toutes les valeurs du caractère on aura alors un caractère quantitatif continu et dans le cas contraire on aura un caractère quantitatif discret.
II. Représentation graphique
II.1 Diagramme en bâtons - Polygone des effectifs
Tableau relatif aux élèves de $3^{eme}$ du Collège Pie XII
II.2 Histogramme - Polygone des effectifs
Tableau relatif aux élèves de $3^{eme}\;F$ du $CEM_{2}$ V. Ndiaye
II.3 Diagramme circulaire
Tableau relatif aux élèves de $3^{eme}$ du Collège Pie XII
On a $360^{o}$ pour $N$(effectif total)
et $\alpha^{o}$ pour $n$(effectif partiel)
Alors $$\alpha^{o}=\dfrac{360^{o}\times n}{N}$$
$$\begin{array}{|c|c|c|c|c|c|c|c|c|}\hline\text{Tailles (en }cm) & 145 & 150 & 154 & 158 & 160 & 162 & 165 & 166 \\ \hline\text{Effectifs }(n) & 1 & 2 & 3 & 6 & 4 & 4 & 3 & 2 \\ \hline\alpha^{o}(\text{angle d'occupation}) & 14.4 & 28.8 & 43.2 & 36.4 & 57.6 & 57.6 & 43.2 & 28.8 \\ \hline\end{array}$$

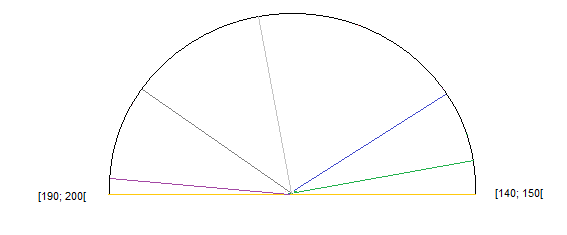
II.4 Diagramme semi-circulaire
Tableau relatif aux élèves de $3^{eme}\;F$ du $CEM_{2}$ V. Ndiaye
On a $180^{o}$ pour $N$(effectif total)
et $\alpha^{o}$ pour $n$(effectif partiel)
Alors $$\alpha^{o}=\dfrac{180^{o}\times n}{N}$$
$$\begin{array}{|c|c|c|c|c|c|c|}\hline\text{Classe de tailles (en }cm) & [140\;;\ 150[ & [150\;;\ 160[ & [160\;;\ 170[ & [170\;;\ 180[ & [180\;;\ 190[ & [190\;;\ 200[ \\ \hline\text{Effectifs }(n) & 3 & 7 & 17 & 13 & 9 & 1 \\ \hline\alpha^{o}(\text{angle d'occupation}) & 10.8 & 25.2 & 61.2 & 46.8 & 32.4 & 3.6 \\ \hline\end{array}$$
III. Paramètres de position
III.1 Mode et classe modale - Fréquence
On appelle mode (ou classe modale) d'une série statistique, la modalité (ou classe) qui a le plus grand effectif.
Exemple :
Dans le tableau relatif aux élèves de $3^{eme}$ du Collège Pie XII, la modalité 158 est le mode de la série statistique. Par contre dans tableau relatif aux élèves de $3^{eme}\;F$ du $CEM_{2}$ V. Ndiaye, la classe [160 ; 170[ est la classe modale.
Remarques
$\cdot\ \ $ Le mode ou la classe modale d'une série statistique peut être déterminée de manière graphique.
$\cdot\ \ $ Dans une série statistique il peut y avoir plusieurs modes ou classes modales.
La fréquence d'une série statistique d'une modalité donnée est égale au rapport de l'effectif partiel de la modalité par l'effectif totale de la population (très souvent multiplié par 100 pour l'avoir en pourcentage).
$\centerdot\ \ $ Tableau des fréquences de la série statistique relatives aux élèves de $3^{eme}$ du Collège Pie XII
$$\begin{array}{|c|c|c|c|c|c|c|c|c|}\hline\text{Modalités (Tailles en }cm) & 145 & 150 & 154 & \boxed{158} & 160 & 162 & 165 & 166 \\ \hline\text{Effectifs }(n) & 1 & 2 & 3 & 6 & 4 & 4 & 3 & 2 \\ \hline\text{Fréquence }(f) & 0.04 & 0.08 & 0.12 & 0.24 & 0.16 & 0.16 & 0.12 & 0.08 \\ \hline\end{array}$$
Le mode de la série statistique est caractérisé par la modalité 158.
$\centerdot\ \ $ Tableau des fréquences de la série statistique relatives aux élèves de $3^{eme}$ du $CEM_{2}$ V. Ndiaye
$$\begin{array}{|c|c|c|c|c|c|c|}\hline\text{Classe de tailles (en }cm) & [140\;;\ 150[ & [150\;;\ 160[ & \boxed{[160\;;\ 170[} & [170\;;\ 180[ & [180\;;\ 190[ & [190\;;\ 200[ \\ \hline\text{Effectifs }(n) & 3 & 7 & 17 & 13 & 9 & 1 \\ \hline f \text{ en }\% & 6 & 14 & 34 & 26 & 18 & 2 \\ \hline\end{array}$$
La classe modale de la série statistique est donnée par la classe [160 ; 170[.
Remarques
La fréquence d'une série statistique donne les mêmes informations que l'effectif.
III.2 Moyenne d'une série statistique
La moyenne d'une série statistique à caractère quantitatif est égale au quotient de la somme de toutes les valeurs prises par le caractère par l'effectif total de la population.
$\centerdot\ \ $ Tableau de calcul de la moyenne de la série statistique relatives aux élèves de $3^{eme}$ du Collège Pie XII
$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|}\hline\text{Modalités (Tailles en }cm) & 145 & 150 & 154 & 158 & 160 & 162 & 165 & 166 & Total \\ \hline\text{Effectifs }(n) & 1 & 2 & 3 & 6 & 4 & 4 & 3 & 2 & 25 \\ \hline\text{"Produits"} & 145 & 300 & 462 & 948 & 640 & 648 & 495 & 332 & 3970 \\ \hline\end{array}$$
La moyenne $$M=\dfrac{\text{total des "Produits"}}{\text{effectif total}}$$
Ainsi, $M=\dfrac{3970}{25}=158.8\;cm$
$\centerdot\ \ $ Si la série statistique est présentée sous forme de classes (intervalles) on prendra les centres de classe comme modalité pour calculer les produits.
$$\begin{array}{|c|c|c|c|c|c|c|c|}\hline\text{Classe de tailles (en }cm) & [140\;;\ 150[ & [150\;;\ 160[ & \boxed{[160\;;\ 170[} & [170\;;\ 180[ & [180\;;\ 190[ & [190\;;\ 200[ & Total \\ \hline\text{Centre de classe} & 145 & 155 & 165 & 175 & 185 & 195 & \\ \hline\text{Effectifs }(n) & 3 & 7 & 17 & 13 & 9 & 1 & 50 \\ \hline\text{"Produits"} & 435 & 1085 & 2805 & 2275 & 1665 & 195 & 8460 \\ \hline\end{array}$$
Ainsi, $M=\dfrac{8460}{50}=169.2\;cm$
III.3 Médiane - Intervalle médian
III.3.1 Effectifs cumulés - Fréquences cumulées
On appelle médiane d'une série statistique à caractère quantitatif, la valeur de ce caractère qui sépare la population en deux parties de même effectif.
Exemple :
Considérons la série statistique brute relative aux élèves de $3^{eme}$ du Collège Pie XII rangée dans l'ordre croissant.
$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline 145 & 150 & 150 & 154 & 154 & 154 & 158 & 158 & 158 & 158 & 158 & 158 & 160 \\ \hline160 & 160 & 160 & 162 & 162 & 162 & 162 & 165 & 165 & 165 & 166 & 166 & \\ \hline\end{array}$$
$13^{e}$ taille de la série statistique.
Remarque :
En éliminant une taille 166 de la série statistique, on aura un intervalle médian [152 ; 160].
III.3.2 Méthode de recherche de la médiane
On appelle effectif cumulé croissant (ou fréquence cumulée croissante) d'une modalité $x$ à caractère quantitatif, la somme des effectifs (fréquences) de ce caractère inférieure ou égale à la modalité $x.$
On appelle effectif cumulé décroissant (ou fréquence cumulée décroissante) d'une modalité $x$ à caractère quantitatif, la somme des effectifs (fréquences) de modalité supérieure ou égale à la modalité $x$
a) Méthode par calcul
Tableau des $E.C.C$ et des $E.C.D$ de la série statistique relative aux élèves de $3^{eme}$ du Collège Pie XII.
$$\begin{array}{|c|c|c|c|c|c|c|c|c|}\hline\text{Modalités (Tailles en }cm) & 145 & 150 & 154 & 158 & 160 & 162 & 165 & 166 \\ \hline\text{Effectifs }(n) & 1 & 2 & 3 & 6 & 4 & 4 & 3 & 2 \\ \hline E.C.C & 1 & 3 & 6 & 12 & 16 & \boxed{20} & 23 & 25 \\ \hline E.C.D & 25 & 24 & 22 & \boxed{19} & \boxed{13} & 9 & 5 & 2 \\ \hline\end{array}$$
$13^{e}$ taille de la série statistique (médiane : modalité 160)
L'effectif cumulé croissant 20 signifie qu'il y a 20 élèves de taille inférieure ou égale à la taille $162\;cm.$
L'effectif cumulé décroissant 19 signifie qu'il y a 19 élèves de taille supérieure ou égale à la taille $158\;cm.$
Tableau des $F.C.C$ et des $F.C.D$ de la série statistique relative aux élèves de $3^{eme}$ du $CEM_{2}$ V. Ndiaye
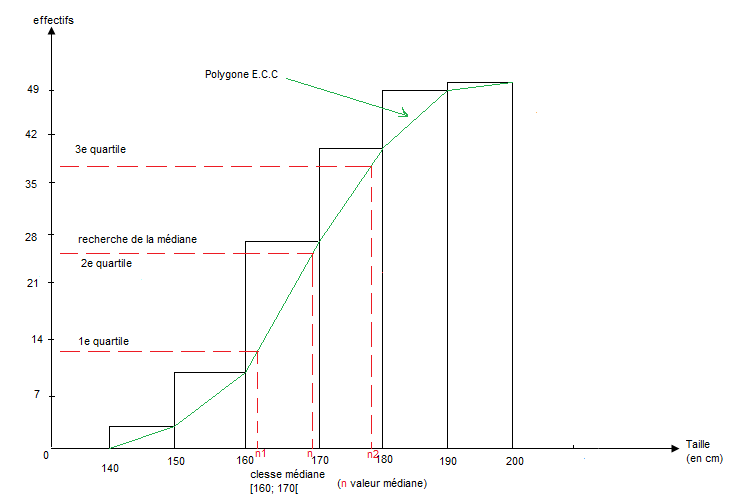
$$\begin{array}{|c|c|c|c|c|c|c|}\hline\text{Classe de tailles (en }cm) & [140\;;\ 150[ & [150\;;\ 160[ & \boxed{[160\;;\ 170[} & [170\;;\ 180[ & [180\;;\ 190[ & [190\;;\ 200[ \\ \hline f \text{ en }\% & 6 & 14 & 34 & 26 & 18 & 2 \\ \hline F.C.C & 6 & 20 & 54 & \boxed{80} & 98 & 100 \\ \hline F.C.D & 100 & 94 & 80 & \boxed{46} & 20 & 2 \\ \hline\end{array}$$
Classe médiane : classe [160 ; 170[
La fréquence cumulée croissante 80 signifie qu'il y a $80\%$ des élèves qui ont eu une taille inférieure ou égale à la taille $180\;cm.$
La fréquence cumulée décroissante 46 signifie qu'il y a $46\%$ des élèves qui ont eu une taille supérieure ou égale à la taille $170\;cm.$
b) Méthode graphique
Diagramme en bâtons des $E.C.C$ de la série statistique relative aux élèves de $3^{eme}$ du Collège Pie XII.
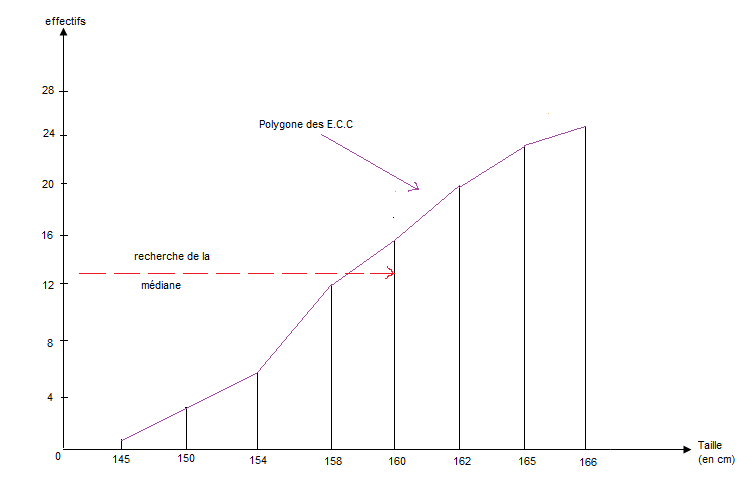
La médiane de la série statistique est la modalité 160.
Histogramme des $F.C.C$ de la série statistique relative aux élèves de $3^{eme}$ du $CEM_{2}$ V. Ndiaye.
Auteur:
Abdoulaye Ba

Commentaires
Anonyme (non vérifié)
ven, 03/01/2019 - 17:10
Permalien
J'adore
Anonyme (non vérifié)
dim, 05/05/2019 - 16:25
Permalien
Vous êtes geniaux
Stéphie (non vérifié)
jeu, 04/16/2020 - 00:09
Permalien
appréciation
Ousmane mboup (non vérifié)
ven, 04/23/2021 - 17:26
Permalien
Merci beaucoup merci
Anonyme (non vérifié)
jeu, 06/09/2022 - 01:00
Permalien
Fff
Anonyme (non vérifié)
mar, 08/02/2022 - 23:37
Permalien
Bien structuré
mayé faye (non vérifié)
mer, 02/15/2023 - 21:41
Permalien
je vous adore.sa me fait
Mamadou Diallo (non vérifié)
mer, 03/22/2023 - 18:10
Permalien
Cours
momy (non vérifié)
mar, 07/11/2023 - 18:39
Permalien
merci
momy (non vérifié)
mar, 07/11/2023 - 18:39
Permalien
merci
momy (non vérifié)
mar, 07/11/2023 - 18:39
Permalien
merci
momy (non vérifié)
mar, 07/11/2023 - 18:39
Permalien
merci
momy (non vérifié)
mar, 07/11/2023 - 18:39
Permalien
merci
momy (non vérifié)
mar, 07/11/2023 - 18:39
Permalien
merci
Anonyme (non vérifié)
jeu, 09/26/2024 - 23:28
Permalien
Merci
Ajouter un commentaire