Vous êtes ici

Solution des exercices : Trigonométrie 3e

Classe:

Troisième

Exercice 1

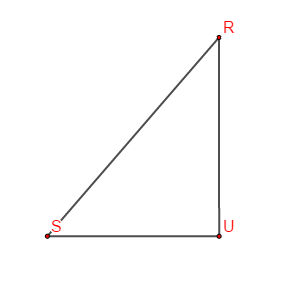
Soit

$RSU$ un triangle rectangle en

$U$ tel que

$RS=3\$ et

$\ SU=2$

1) Calculons

$RU$

$RSU$ rectangle en

$U$ , alors d'après le théorème de Pythagore on a :

$RS^{2}=RU^{2}+SU^{2}$

Donc,

$\begin{array}{rcl} RU^{2}&=&RS^{2}-SU^{2}\\ \\&=&3^{2}-2^{2}\\\\&=&9-4\\\\&=&5 \end{array}$

D'où,

$RU=\sqrt{5}$

2) Calculons

$\cos\widehat{R}\;,\ \sin\widehat{R}\;,\ \cos\widehat{S}\;,\ \sin\widehat{S}\$ et

$\ \tan\widehat{S}$

On a :

$\cos\widehat{R}=\dfrac{RU}{RS}=\dfrac{\sqrt{5}}{3}$

$\sin\widehat{R}=\dfrac{SU}{RS}=\dfrac{2}{3}$

$\cos\widehat{S}=\dfrac{SU}{RS}=\dfrac{2}{3}$

$\sin\widehat{S}=\dfrac{RU}{RS}=\dfrac{\sqrt{5}}{3}$

Autrement, comme

$RSU$ est rectangle en

$U$ alors

$\widehat{R}\$ et

$\ \widehat{S}$ sont complémentaires.

Donc,

$\cos\widehat{S}=\sin\widehat{R}\$ et

$\ \sin\widehat{S}=\cos\widehat{R}$

D'où,

$\cos\widehat{S}=\dfrac{2}{3}\$ et

$\ \sin\widehat{S}=\dfrac{\sqrt{5}}{3}$

On a :

$\begin{array}{rcl}\tan\widehat{S}&=&\dfrac{\sin\widehat{S}}{\cos\widehat{S}}\\ \\&=&\dfrac{\dfrac{\sqrt{5}}{3}}{\dfrac{2}{3}}\\\\&=&\dfrac{\sqrt{5}\times 3}{3\times 2}\\\\&=&\dfrac{\sqrt{5}}{2}\end{array}$

Donc,

$\tan\widehat{S}=\dfrac{\sqrt{5}}{2}$

Exercice 2

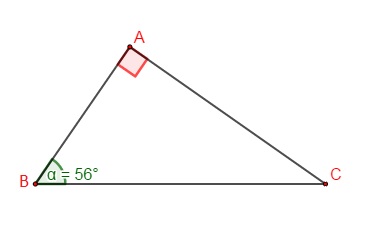
1) Soit

$ABC$ un triangle rectangle en

$A$ tel que

$\widehat{ABC}=56^{o}\$ et

$\ BC=4.2\;cm.$

Calculons

$AB$

On a :

$\cos\widehat{ABC}=\dfrac{AB}{BC}$

donc,

$AB=BC\times\cos\widehat{ABC}$

comme

$\widehat{ABC}=56^{o}$ alors,

$\cos\widehat{ABC}=\cos 56^{o}=0.56$

ainsi,

$AB=BC\times 0.56=4.2\times 0.56=2.35$

d'où,

$\boxed{AB=2.35\;cm}$

Calculons

$AC$

On a :

$\sin\widehat{ABC}=\dfrac{AC}{BC}$

donc,

$AC=BC\times\sin\widehat{ABC}$

or,

$\sin\widehat{ABC}=\sin 56^{o}=0.83$

ainsi,

$AC=BC\times 0.83=4.2\times 0.83=3.49$

d'où,

$\boxed{AC=3.49\;cm}$

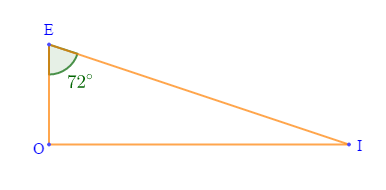
2) Construisons un triangle

$OIE$ rectangle en

$O$ tel que

$\widehat{OEI}=72^{o}\$ et

$\ OE=2\;cm.$

Calculons l'arrondi au dixième près de

$OI.$

On a :

$\tan\widehat{OEI}=\dfrac{OI}{OE}$

donc,

$OI=OE\times\tan\widehat{OEI}$

or,

$\tan\widehat{OEI}=\tan 72^{o}\simeq 3.08$

ainsi,

$OI=OE\times 3.08=2\times 3.08=6.1$

d'où,

$\boxed{OI=6.1\;cm}$

En vérifiant sur la figure, on obtient la même mesure pour

$OI.$

Exercice 3

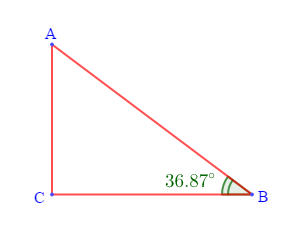
$ABC$ est un triangle rectangle en

$C$ tel que :

$CB=4\;cm\$ et

$\ AC=3\;cm.$

Calculons

$\sin\widehat{B}$

On a :

$\sin\widehat{B}=\dfrac{AC}{AB}$

comme

$ABC$ est rectangle en

$C$ alors, d'après le théorème de Pythagore on a :

$AB^{2}=AC^{2}+CB^{2}$

donc,

$\begin{array}{rcl} AB&=&\sqrt{AC^{2}+CB^{2}}\\\\&=&\sqrt{9+16}\\\\&=&\sqrt{25}\\\\&=&5\end{array}$

ainsi,

$\sin\widehat{B}=\dfrac{3}{5}=0.6$

d'où,

$\boxed{\sin\widehat{B}=0.6}$

Calculons

$\cos\widehat{B}$

On a :

$\cos\widehat{B}=\dfrac{CB}{AB}$

donc,

$\cos\widehat{B}=\dfrac{4}{5}=0.8$

ainsi,

$\boxed{\cos\widehat{B}=0.8}$

Calculons

$\tan\widehat{B}$

On sait que

$\tan\widehat{B}=\dfrac{\sin\widehat{B}}{\cos\widehat{B}}$

alors,

$\tan\widehat{B}=\dfrac{0.6}{0.8}=0.75$

On en déduit alors,

$\boxed{mes\;\widehat{B}=36.8^{\circ}}$

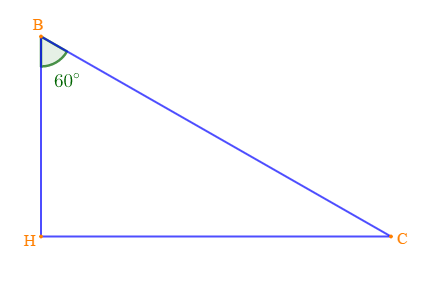
2) Considérons le triangle

$HBC$ rectangle en

$H$ tel que

$mes\;\widehat{B}=60^{\circ}\$ et

$\ HB=4\;cm$

Calculons la distance

$BC$

Comme

$\cos\widehat{B}=\dfrac{HB}{BC}$ alors,

$BC\times\cos\widehat{B}=HB$

donc,

$BC=\dfrac{HB}{\cos\widehat{B}}$

or,

$\cos\widehat{B}=\cos 60^{\circ}=0.5$

ainsi,

$BC=\dfrac{4}{0.5}=8$

d'où,

$\boxed{BC=8\;cm}$

Calculons la distance

$HC$

On sait que

$\sin\widehat{B}=\dfrac{HC}{BC}$

ce qui entraine alors,

$HC=BC\times\sin\widehat{B}$

or,

$\sin\widehat{B}=\dfrac{\sqrt{3}}{2}$

donc,

$HC=8\times\dfrac{\sqrt{3}}{2}=4\sqrt{3}$

Ainsi,

$\boxed{HC=4\sqrt{3}\;cm}$

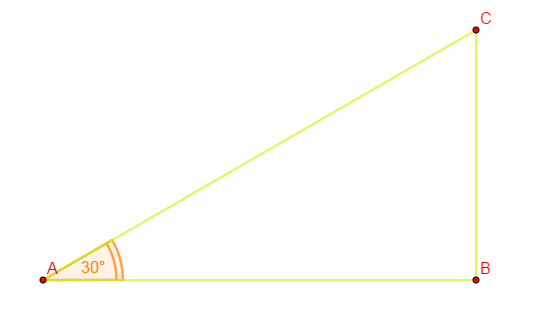
3) Considérons un triangle

$ABC$ rectangle en

$B$ tel que :

$mes\widehat{A}=30^{\circ}\quad$ et

$\quad CB=5\;cm.$

Calculons

$AC$

On a :

$\sin\widehat{A}=\dfrac{CB}{AC}$

donc,

$AC\times\sin\widehat{A}=CB$

ce qui entraine alors,

$AC=\dfrac{CB}{\sin\widehat{A}}\$ avec

$\ \sin\widehat{A}=\sin 30^{\circ}=\dfrac{1}{2}$

ainsi,

$AC=2CB=10$

d'où,

$\boxed{AC=10\;cm}$

Calculons

$AB$

Pour cela, on peut soit utiliser le théorème de Pythagore :

$AC^{2}=AB^{2}+CB^{2}$

soit exploiter tout simplement le cosinus de l'angle

$\widehat{A}$

et dans ce cas on aura :

$\cos\widehat{A}=\dfrac{AB}{AC}$

donc,

$AB=AC\times\cos\widehat{A}\$ avec

$\ \cos\widehat{A}=\cos 30^{\circ}=\dfrac{\sqrt{3}}{2}$

par suite,

$AB=10\times\dfrac{\sqrt{3}}{2}$

ainsi,

$\boxed{AB=5\sqrt{3}\;cm}$

4) Soit

$STV$ un triangle rectangle en

$T$ tel que :

$\tan\widehat{S}=\dfrac{4}{3}\quad$ et

$\quad TV=\sqrt{6}\;cm.$

Calculons

$ST$

On sait que

$\tan\widehat{S}=\dfrac{TV}{ST}=\dfrac{4}{3}$

donc,

$ST\times 4=TV\times 3$

par suite,

$ST=\dfrac{TV\times 3}{4}$

ainsi,

$ST=\dfrac{\sqrt{6}\times 3}{4}=\dfrac{3\sqrt{6}}{4}$

ce qui donne,

$\boxed{ST=\dfrac{3\sqrt{6}}{4}\;cm}$

Calculons

$SV$

$STV$ étant rectangle en

$T$ alors, en utilisant le théorème de Pythagore on aura :

$SV^{2}=ST^{2}+TV^{2}$

et par suite :

$\begin{array}{rcl} SV&=&\sqrt{ST^{2}+TV^{2}}\\\\&=&\sqrt{\left(\dfrac{3\sqrt{6}}{4}\right)^{2}+(\sqrt{6})^{2}}\\ \\&=&\sqrt{\dfrac{54}{16}+6}\\ \\&=&\dfrac{\sqrt{54+96}}{4}\\ \\&=&\dfrac{5\sqrt{6}}{4}\end{array}$

d'où

$\boxed{SV=\dfrac{5\sqrt{6}}{4}\;cm}$

5) Dans le triangle

$ABC$ rectangle en

$B$ , on donne :

$\sin\widehat{A}=\dfrac{\sqrt{5}}{3}.$

Calculons

$\cos\widehat{A}$

$\widehat{A}$ un angle aigu alors on a :

$\cos^{2}\widehat{A}+\sin^{2}\widehat{A}=1$

ainsi,

$\begin{array}{rcl} \cos\widehat{A}&=&\sqrt{1-\sin^{2}\widehat{A}}\\\\&=&\sqrt{1-\dfrac{5}{9}}\\ \\&=&\sqrt{\dfrac{9-5}{9}}\\ \\&=&\sqrt{\dfrac{4}{9}}\\ \\&=&\dfrac{2}{3}\end{array}$

d'où,

$\boxed{\cos\widehat{A}=\dfrac{2}{3}}$

Calculons

$\tan\widehat{A}$

On a :

$\begin{array}{rcl}\tan\widehat{A}&=&\dfrac{\sin\widehat{A}}{\cos\widehat{A}}\\\\&=&\dfrac{\dfrac{\sqrt{5}}{3}}{\dfrac{2}{3}}\\ \\&=&\dfrac{\sqrt{5}\times 3}{3\times 2}\\ \\&=&\dfrac{\sqrt{5}}{2}\end{array}$

6) Soit

$\widehat{A}\quad$ et

$\quad\widehat{B}$ deux angles aigus tels que :

$\cos\widehat{A}=\dfrac{\sqrt{3}-1}{6}\$ et

$\ \sin\widehat{B}=\dfrac{\sqrt{6}-\sqrt{2}}{\sqrt{72}}$

Montrons que

$\widehat{A}\$ et

$\ \widehat{B}$ sont deux angles complémentaires.

On sait que si deux angles aigus

$\widehat{A}\$ et

$\ \widehat{B}$ sont complémentaires alors,

$\cos\widehat{A}=\sin\widehat{B}$

On a :

$\begin{array}{rcl}\sin\widehat{B}&=&\dfrac{\sqrt{6}-\sqrt{2}}{\sqrt{72}}\\\\&=&\dfrac{\sqrt{6}-\sqrt{2}}{6\sqrt{2}}\\ \\&=&\dfrac{(\sqrt{6}-\sqrt{2})\times\sqrt{2}}{12}\\ \\&=&\dfrac{\sqrt{12}-2}{12}\\ \\&=&\dfrac{2\sqrt{3}-2}{12}\\ \\&=&\dfrac{\sqrt{3}-1}{6}\end{array}$

On voit bien que

$\sin\widehat{B}=\cos\widehat{A}=\dfrac{\sqrt{3}-1}{6}.$

Ce qui montre que

$\widehat{A}\$ et

$\ \widehat{B}$ sont deux angles complémentaires.

Exercice 4

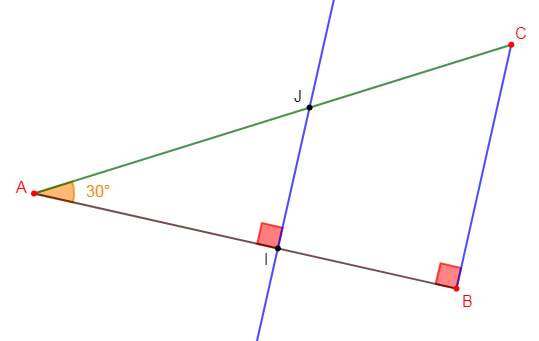
$ABC$ est un triangle rectangle en

$B$ tel que

$AC=10\;cm\$ et

$\ BC=5\;cm.\ I$ est un point de

$[AB]$ tel que

$AI=5\;cm.$ La perpendiculaire à

$(AB)$ passant par

$I$ coupe

$[AC]$ en

$J.$

1) En utilisant le sinus de

$\widehat{BAC}$ , montrons que

$\dfrac{IJ}{AJ}=\dfrac{BC}{AC}$ puis, calculons

$IJ.$

En effet, comme le triangle

$ABC$ est rectangle en

$B$ alors, on a :

$\sin\widehat{BAC}=\dfrac{BC}{AC}\qquad(\text{égalité 1})$

Par ailleurs, on sait que la droite

$(IJ)$ est perpendiculaire à la droite

$(AB)$ en

$I.$

Donc, le triangle

$AIJ$ est rectangle en

$I.$

Par suite, le sinus de l'angle

$\widehat{BAC}$ peut encore s'écrire :

$\sin\widehat{BAC}=\dfrac{IJ}{AJ}\qquad(\text{égalité 2})$

Ainsi, en comparant les égalités

$(1)\$ et

$\ (2)$ , on obtient :

$\dfrac{IJ}{AJ}=\dfrac{BC}{AC}$

$-\$ Calcul de

$IJ$

En effet, les droites

$(IJ)\$ et

$\ (BC)$ sont perpendiculaires à la même droite

$(AB).$

Donc,

$(IJ)\$ et

$\ (BC)$ sont parallèles.

Par suite, les triangles

$ABC\$ et

$\ AIJ$ sont en position de Thalès.

Ainsi, en utilisant le théorème de Thalès, on obtient :

$\dfrac{IJ}{BC}=\dfrac{AI}{AB}$

Ce qui donne :

$IJ=\dfrac{AI\times BC}{AB}$

Déterminons alors la longueur

$AB$

Le triangle

$ABC$ étant rectangle en

$B$ alors, d'après le théorème de Pythagore, on a :

$AB^{2}+BC^{2}=AC^{2}$

Ce qui entraine :

$AB^{2}=AC^{2}-BC^{2}$

Ainsi,

$\begin{array}{rcl} AB&=&\sqrt{AC^{2}-BC^{2}}\\\\&=&\sqrt{(10)^{2}-(5)^{2}}\\\\&=&\sqrt{100-25}\\\\&=&\sqrt{75}\\\\&=&\sqrt{25\times 3}\\\\&=&\sqrt{25}\times\sqrt{3}\\\\&=&5\sqrt{3}\end{array}$

Donc,

$\boxed{AB=5\sqrt{3}\;cm}$

Remplaçons alors

$AB\;,\ BC\$ et

$\ AI$ par leur valeur, dans l'expression de

$IJ.$

On trouve :

$\begin{array}{rcl} IJ&=&\dfrac{AI\times BC}{AB}\\\\&=&\dfrac{5\times 5}{5\sqrt{3}}\\\\&=&\dfrac{5}{\sqrt{3}}\\\\&=&\dfrac{5\times\sqrt{3}}{\sqrt{3}\times\sqrt{3}}\\\\&=&\dfrac{5\sqrt{3}}{3}\end{array}$

$\boxed{IJ=\dfrac{5\sqrt{3}}{3}\;cm}$

2) Calculons

$\sin\widehat{BAC}$ et en déduisons sa mesure en degrés.

Le triangle

$ABC$ étant rectangle en

$B$ alors, on a :

$\sin\widehat{BAC}=\dfrac{BC}{AC}$

En remplaçant

$BC\$ et

$\ AC$ par leur valeur, on obtient :

$\sin\widehat{BAC}=\dfrac{5}{10}=\dfrac{1}{2}$

Ainsi,

$\boxed{\sin\widehat{BAC}=\dfrac{1}{2}}$

Comme

$\widehat{BAC}$ est un angle aigu dont le sinus est égal à

$\dfrac{1}{2}$ alors, sa mesure est de

$30^{\circ}.$

D'où,

$\boxed{mes\;\widehat{BAC}=30^{\circ}}$

Exercice 5

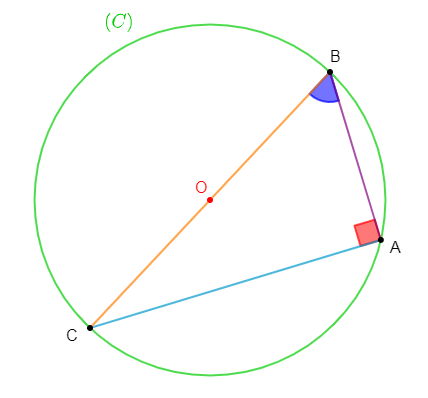
$(C)$ est un cercle de centre

$O$ et de rayon

$r. \ [BC]$ est un diamètre du cercle et

$A$ un point de

$(C)$ tel que

$AB=r.$

1) Montrons que le triangle

$ABC$ est rectangle en

$A.$

Comme

$[BC]$ est un diamètre du cercle alors, les points

$B\$ et

$\ C$ sont sur le cercle

$(C).$

Aussi,

$A$ est un point de

$(C).$

Donc,

$ABC$ est un triangle inscrit dans le cercle

$(C)$ et dont le côté

$[BC]$ est un diamètre de ce cercle.

Par conséquent, c'est un triangle rectangle en

$A.$

2) Calculons

$AC$ en fonction de

$r.$

Le triangle

$ABC$ étant rectangle en

$A$ alors, en utilisant le théorème de Pythagore, on a :

$AC^{2}+AB^{2}=BC^{2}$

Ce qui entraine :

$AC^{2}=BC^{2}-AB^{2}$

Comme

$[BC]$ est un diamètre du cercle

$(C)$ de rayon

$r$ alors,

$BC=2r.$

Donc, en remplaçant

$BC\$ et

$\ AB$ par leur valeur, on obtient :

$\begin{array}{rcl} AC&=&\sqrt{BC^{2}-AB^{2}}\\\\&=&\sqrt{(2r)^{2}-(r)^{2}}\\\\&=&\sqrt{4r^{2}-r^{2}}\\\\&=&\sqrt{3r^{2}}\\\\&=&\sqrt{r^{2}\times 3}\\\\&=&\sqrt{r^{2}}\times\sqrt{3}\\\\&=&|r|\sqrt{3}\\\\&=&r\sqrt{3}\end{array}$

Donc,

$\boxed{AC=r\sqrt{3}\;cm}$

3) Calculons le sinus de l'angle

$\widehat{ABC}.$

Le triangle

$ABC$ étant rectangle en

$A$ alors, le sinus de l'angle

$\widehat{ABC}$ est donné par :

$\sin\widehat{ABC}=\dfrac{AC}{BC}$

En remplaçant,

$AB\$ et

$\ BC$ par leur valeur, on trouve :

$\begin{array}{rcl} \sin\widehat{ABC}&=&\dfrac{r\sqrt{3}}{2r}\\\\&=&\dfrac{\sqrt{3}}{2}\end{array}$

Ainsi,

$\boxed{\sin\widehat{ABC}=\dfrac{\sqrt{3}}{2}}$

Exercice 6

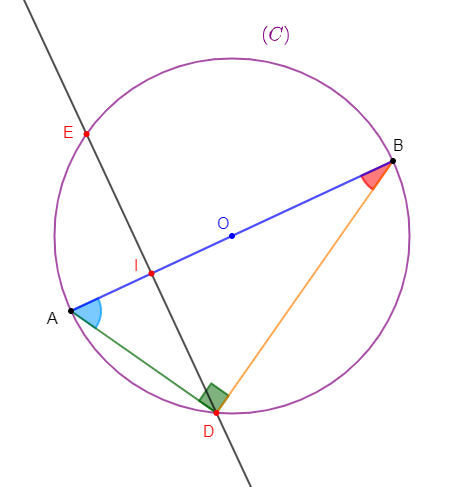
Soit un cercle

$(C)$ de centre

$O$ et de rayon

$r$ .

$\ [AB]$ est un diamètre de ce cercle et

$I$ milieu de

$[OA].$ La perpendiculaire à la droite

$(AB)$ passant par

$I$ coupe le cercle en deux points

$D\$ et

$\ E.$

1) Démontrons que

$ABD$ est un triangle rectangle puis, montrons que

$AD=r.$

En effet,

$[AB]$ est un diamètre du cercle

$(C)$ alors, les extrémités

$A\$ et

$\ B$ sont sur ce cercle.

Aussi, le point

$D$ appartient au cercle

$(C).$

Donc,

$ABD$ est un triangle inscrit dans le cercle

$(C)$ et dont le côté

$[AB]$ est un diamètre de ce cercle.

Par conséquent,

$ABD$ est un triangle rectangle en

$D.$

Montrons que

$AD=r.$

On a :

$ABD$ est un triangle rectangle en

$D$ et la droite

$(ID)$ est perpendiculaire à la droite

$(BC)$ en

$I.$

Donc,

$(ID)$ est la hauteur issue de

$D$ et le point

$I$ est le pied de cette hauteur sur

$[AB].$

Ainsi, en utilisant la deuxième relation métrique, on obtient :

$AD^{2}=AI\times AB$

Or,

$[AB]$ est un diamètre du cercle

$(C)$ de rayon

$r$ donc,

$AB=2r.$

De plus,

$I$ est milieu de

$[OA].$

Ce qui signifie que

$AI=\dfrac{OA}{2}=\dfrac{r}{2}.$

En remplaçant

$AI\$ et

$\ AB$ par leur valeur, on trouve :

$\begin{array}{rcl} AD^{2}&=&AI\times AB\\\\&=&\dfrac{r}{2}\times 2r\\\\&=&\dfrac{2r^{2}}{2}\\\\&=&r^{2}\end{array}$

Ainsi,

$\begin{array}{rcl} AD&=&\sqrt{r^{2}}\\\\&=&|r|\\\\&=&r\end{array}$

D'où,

$\boxed{AD=r}$

2) Calculons

$\cos\widehat{DAB}.$

Comme le triangle

$ABD$ est rectangle en

$D$ alors, le cosinus de l'angle

$\widehat{DAB}$ est donné par :

$\cos\widehat{DAB}=\dfrac{AD}{AB}$

En remplaçant,

$AD\$ et

$\ AB$ par leur valeur, on obtient :

$\begin{array}{rcl} \cos\widehat{DAB}&=&\dfrac{r}{2r}\\\\&=&\dfrac{1}{2}\end{array}$

Donc,

$\boxed{\cos\widehat{DAB}=\dfrac{1}{2}}$

En déduisons

$\sin\widehat{DBO}.$

En effet, dans un triangle rectangle, les angles aigus sont complémentaires.

Donc, les angles

$\widehat{DAB}\$ et

$\ \widehat{DBO}$ sont complémentaires.

Or, si deux angles sont complémentaires alors, le sinus de l'un est égal au cosinus de l'autre.

Ce qui signifie que :

$\sin\widehat{DBO}=\cos\widehat{DAB}=\dfrac{1}{2}$

D'où,

$\boxed{\sin\widehat{DBO}=\dfrac{1}{2}}$

3) Démontrons que

$\dfrac{AI^{2}}{AD^{2}}+\dfrac{DB^{2}}{AB^{2}}=1$

On a :

$\dfrac{AI^{2}}{AD^{2}}+\dfrac{DB^{2}}{AB^{2}}=\left(\dfrac{AI}{AD}\right)^{2}+\left(\dfrac{DB}{AB}\right)^{2}$

Or, on remarque que :

$\dfrac{AI}{AD}=\cos\widehat{DAB}$

$\dfrac{DB}{AB}=\sin\widehat{DAB}$

Donc, en remplaçant

$\dfrac{AI}{AD}\$ et

$\ \dfrac{DB}{AB}$ par leur expression, on obtient :

$\left(\dfrac{AI}{AD}\right)^{2}+\left(\dfrac{DB}{AB}\right)^{2}=\left(\cos\widehat{DAB}\right)^{2}+\left(\sin\widehat{DAB}\right)^{2}=1$

D'où,

$\boxed{\dfrac{AI^{2}}{AD^{2}}+\dfrac{DB^{2}}{AB^{2}}=1}$

Exercice 7

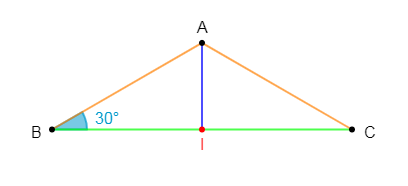
Soit

$ABC$ un triangle isocèle de sommet

$A$ tel que

$\widehat{B}= 30^{\circ}\$ et

$\ BC=6\;cm.$ On appelle

$I$ milieu de

$[BC].$

1) Calculons

$AB\$ et

$\ AI$

$-\$ Calcul de

$AB$

Comme

$ABC$ est un triangle isocèle de sommet

$A\$ et

$\ I$ milieu de

$[BC]$ alors,

$(AI)$ est la hauteur issue de

$A.$

Donc,

$(AI)$ est perpendiculaire à

$(BC).$

Par suite,

$ABI$ est un triangle rectangle en

$I.$

Ainsi, en utilisant le cosinus de l'angle

$\widehat{B}$ , on obtient :

$\cos\widehat{B}=\dfrac{BI}{AB}$

Ce qui donne :

$AB=\dfrac{BI}{\cos\widehat{B}}$

Or,

$\widehat{B}= 30^{\circ}\$ et

$\ BI=\dfrac{BC}{2}$

Donc,

$\cos\widehat{B}=\cos 30^{\circ}=\dfrac{\sqrt{3}}{2}\$ et

$\ BI=\dfrac{6}{2}=3$

En remplaçant

$BI\$ et

$\ \cos\widehat{B}$ par leur valeur, dans l'expression de

$AB$ , on trouve :

$\begin{array}{rcl} AB&=&\dfrac{BI}{\cos\widehat{B}}\\\\&=&\dfrac{3}{\dfrac{\sqrt{3}}{2}}\\\\&=&3\times\dfrac{2}{\sqrt{3}}\\\\&=&\dfrac{6}{\sqrt{3}}\\\\&=&\dfrac{6\sqrt{3}}{3}\\\\&=&2\sqrt{3}\end{array}$

D'où,

$\boxed{AB=2\sqrt{3}\;cm}$

$-\$ Calcul de

$AI$

Comme

$ABI$ est un triangle rectangle en

$I$ alors, en utilisant le sinus de l'angle

$\widehat{B}$ , on obtient :

$\sin\widehat{B}=\dfrac{AI}{AB}$

Ce qui donne :

$AI=AB\times\sin\widehat{B}$

Or,

$\sin\widehat{B}=\sin 30^{\circ}=\dfrac{1}{2}.$

Donc, en remplaçant

$AB\$ et

$\ \sin\widehat{B}$ par leur valeur, dans l'expression de

$AI$ , on trouve :

$\begin{array}{rcl} AI&=&AB\times\sin\widehat{B}\\\\&=&2\sqrt{3}\times\dfrac{1}{2}\\\\&=&\dfrac{2\sqrt{3}}{2}\\\\&=&\sqrt{3}\end{array}$

Ainsi,

$\boxed{AI=\sqrt{3}\;cm}$

2) Calculons l'aire

$S$ du triangle

$ABC$ puis, donnons son encadrement à

$0.1\;cm^{2}$ près sachant que

$1.732<\sqrt{3}<1.733$

$-\$ Calcul de l'aire

$S$ du triangle

$ABC$

En effet, on sait que l'aire

$S$ d'un triangle est donnée par :

$S=\dfrac{\text{Base}\times\text{Hauteur}}{2}$

Ainsi, pour le triangle

$ABC$ , on a :

$S=\dfrac{BC\times AI}{2}$

En remplaçant

$BC\$ et

$\ AI$ par leur valeur, on obtient :

$\begin{array}{rcl} S&=&\dfrac{BC\times AI}{2}\\\\&=&\dfrac{6\times \sqrt{3}}{2}\\\\&=&\dfrac{6\sqrt{3}}{2}\\\\&=&3\sqrt{3}\end{array}$

D'où,

$\boxed{S=3\sqrt{3}\;cm^{2}}$

$-\$ Encadrement de

$S$

Soit :

$S=3\sqrt{3}$

On a :

$1.732<\sqrt{3}<1.733$

Alors, en multipliant chaque membre de cette inégalité par

$3$ , on trouve :

$3\times 1.732<3\times\sqrt{3}<3\times 1.733$

Ce qui donne :

$5.196<3\sqrt{3}<5.199$

D'où, un encadrement à

$0.1\;cm^{2}$ près est donné par :

$\boxed{5.1<S<5.2}$

Exercice 8

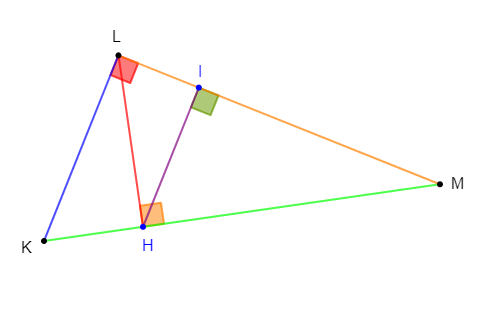
$KLM$ est un triangle

$KL=4\;cm\;;\ LM=4\sqrt{3}\;;\ KM=8\;cm.$

1) Montrons que

$KLM$ est un triangle rectangle.

Calculons les carrés des longueurs des côtés du triangle

$KLM.$

On a :

$KM^{2}=8^{2}=64$

$KL^{2}=4^{2}=16$

$LM^{2}=(4\sqrt{3})^{2}=16\times 3=48$

Alors,

$KL^{2}+LM^{2}=16+48=64$

Nous remarquons que

$KL^{2}+LM^{2}=KM^{2}$

Donc, d'après la réciproque du théorème de Pythagore, le triangle

$KLM$ est rectangle en

$L.$

2) Faisons une figure.

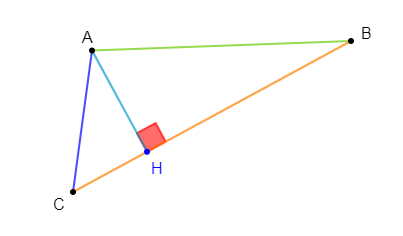
3) Calculons

$LH\$ et

$\ KH\;,\ H$ étant le projeté orthogonal de

$L$ sur

$(KM).$

$-\$ Calcul de

$LH$

Comme

$KLM$ est un triangle rectangle en

$L$ alors, le sinus de l'angle

$\widehat{MKL}$ est donné par :

$\sin\widehat{MKL}=\dfrac{LM}{KM}\qquad(\text{égalité 1})$

Par ailleurs,

$H$ est le projeté orthogonal de

$L$ sur

$(KM)$ donc,

$(LH)$ est la hauteur issue de

$L.$

Ainsi,

$KLH$ est aussi un triangle rectangle en

$H.$

Par suite, le sinus de l'angle

$\widehat{MKL}$ est encore donné par :

$\sin\widehat{MKL}=\dfrac{LH}{KL}\qquad(\text{égalité 2})$

En comparant les égalité

$(1)\$ et

$\ (2)$ , on trouve :

$\dfrac{LH}{KL}=\dfrac{LM}{KM}$

Ce qui entraine :

$LH=\dfrac{LM\times KL}{KM}$

En remplaçant

$LM\;,\ KL\$ et

$\ KM$ par leur valeur, on obtient :

$\begin{array}{rcl} LH&=&\dfrac{LM\times KL}{KM}\\\\&=&\dfrac{4\sqrt{3}\times 4}{8}\\\\&=&\dfrac{16\sqrt{3}}{8}\\\\&=&2\sqrt{3}\end{array}$

D'où,

$\boxed{LH=2\sqrt{3}\;cm}$

$-\$ Calcul de

$KH$

Le triangle

$KLM$ étant rectangle en

$L$ alors, en utilisant la deuxième relation métrique, on trouve :

$KL^{2}=KH\times KM$

Par suite,

$KH=\dfrac{KL^{2}}{KM}$

En remplaçant

$KL\$ et

$\ KM$ par leur valeur, on obtient :

$\begin{array}{rcl} KH&=&\dfrac{KL^{2}}{KM}\\\\&=&\dfrac{4^{2}}{8}\\\\&=&\dfrac{16}{8}\\\\&=&2\end{array}$

D'où,

$\boxed{KH=2\;cm}$

4) Soit

$I$ le projeté orthogonal de

$H$ sur

$(ML).$ Calculons

$IH.$

Comme

$I$ le projeté orthogonal de

$H$ sur

$(ML)$ alors,

$(IH)$ est perpendiculaire à

$(LM).$

Ainsi,

$(KL)\$ et

$\ (IH)$ sont deux droites perpendiculaires à une même droite

$(LM).$

Donc, elles sont parallèles.

Par suite, les triangles

$KLM\$ et

$\ MHI$ sont en position de Thalès.

Ainsi, en appliquant le théorème de Thalès, on a :

$\dfrac{IH}{KL}=\dfrac{MH}{KM}$

Ce qui entraine :

$IH=\dfrac{MH\times KL}{KM}$

Or,

$MH=KM-KH=8-2=6\;cm$

Donc, en remplaçant

$MH\;,\ KL\$ et

$\ KM$ par leur valeur, on obtient :

$\begin{array}{rcl} IH&=&\dfrac{MH\times KL}{KM}\\\\&=&\dfrac{6\times 4}{8}\\\\&=&\dfrac{24}{8}\\\\&=&3\end{array}$

D'où,

$\boxed{IH=3\;cm}$

Exercice 9

1) On donne une valeur trigonométrique déduisons-en les autres :

Soit :

$\cos x=\dfrac{1}{4}$

On sait que :

$\cos^{2}x+\sin^{2}x=1$

Ce qui entraine :

$\sin^{2}x=1-\cos^{2}x$

Ainsi,

$\sin x=\sqrt{1-\cos^{2}x}$

Donc, en remplaçant

$\cos x$ par sa valeur

$\dfrac{1}{4}$ , on obtient :

$\begin{array}{rcl} \sin x&=&\sqrt{1-\cos^{2}x}\\\\&=&\sqrt{1-\left(\dfrac{1}{4}\right)^{2}}\\\\&=&\sqrt{1-\dfrac{1}{16}}\\\\&=&\sqrt{\dfrac{16}{16}-\dfrac{1}{16}}\\\\&=&\sqrt{\dfrac{15}{16}}\\\\&=&\dfrac{\sqrt{15}}{\sqrt{16}}\\\\&=&\dfrac{\sqrt{15}}{4}\end{array}$

D'où,

$\boxed{\sin x=\dfrac{\sqrt{15}}{4}}$

On a :

$\tan x=\dfrac{\sin x}{\cos x}$

Alors, en remplaçant

$\sin x\$ et

$\ \cos x$ par leur valeur, on trouve :

$\begin{array}{rcl} \tan x&=&\dfrac{\sin x}{\cos x}\\\\&=&\dfrac{\dfrac{\sqrt{15}}{4}}{\dfrac{1}{4}}\\\\&=&\dfrac{\sqrt{15}}{4}\times\dfrac{4}{1}\\\\&=&\sqrt{15}\end{array}$

Donc,

$\boxed{\tan x=\sqrt{15}}$

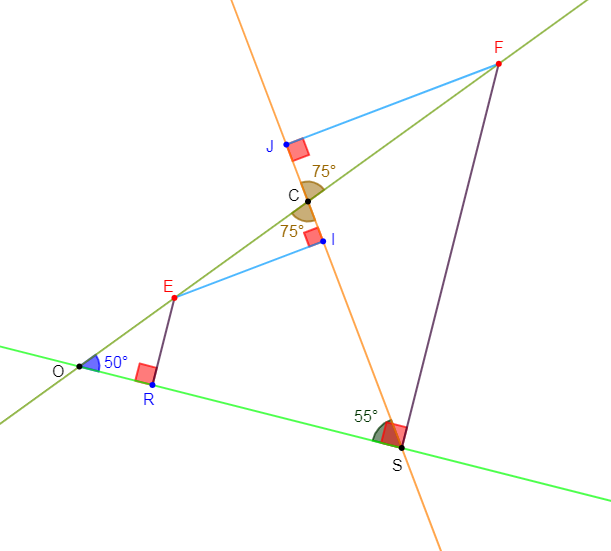
2) Construisons un triangle

$COS$ tel que

$\widehat{OCS}=75^{\circ}\$ et

$\ \widehat{CSO}=55^{\circ}.$

Plaçons deux points

$E\$ et

$\ F$ sur la droite

$(CO)$ tels que

$S$ soit le projeté orthogonal de

$F$ sur

$(OS)\$ et

$\ EF=8\;cm.$

Plaçons le point

$R$ projeté orthogonal de

$E$ sur

$(OS).$ On appelle

$I\$ et

$\ J$ les projetés orthogonaux respectifs de

$E\$ et

$\ F$ sur

$(CS).$

Calculons les arrondis au dixième de

$IJ\$ et

$\ RS.$

$-\$ Calcul de

$IJ$

En effet, comme

$I\$ et

$\ J$ sont les projetés orthogonaux respectifs de

$E\$ et

$\ F$ sur

$(CS)$ alors, les triangles

$EIC\$ et

$\ FJC$ sont rectangles respectivement en

$I\$ et

$\ J.$

Ainsi, on a :

$\cos\widehat{ECI}=\dfrac{IC}{EC}\ \Rightarrow\ IC=EC\times\cos\widehat{ECI}$

$\cos\widehat{FCJ}=\dfrac{JC}{FC}\ \Rightarrow\ JC=FC\times\cos\widehat{FCJ}$

Or,

$\cos\widehat{ECI}=\cos\widehat{FCJ}=\cos 75^{\circ}$

Par ailleurs, on sait que :

$IJ=IC+JC.$

Alors, en remplaçant

$IC\$ et

$\ JC$ par leur expression, on trouve :

$\begin{array}{rcl} IJ&=&IC+JC\\\\&=&EC\times\cos\widehat{ECI}+FC\times\cos\widehat{FCJ}\\\\&=&EC\times\cos 75^{\circ}+FC\times\cos 75^{\circ}\\\\&=&\cos 75^{\circ}\times(EC+FC)\\\\&=&\cos 75^{\circ}\times EF\end{array}$

Donc,

$\boxed{IJ=EF\times\cos 75^{\circ}}$

Or,

$EF=8\;cm\$ et

$\ \cos 75^{\circ}=0.2588$

Par suite,

$\begin{array}{rcl} IJ&=&EF\times\cos 75^{\circ}\\\\&=&8\times 0.2588\\\\&=&2.0704\end{array}$

D'où, en arrondissant au dixième près, on trouve :

$\boxed{IJ\simeq 2.1\;cm}$

$-\$ Calcul de

$RS$

En effet, on sait que dans un triangle la somme des angles est égale à

$180^{\circ}.$

Donc,

$\widehat{COS}+\widehat{OCS}+\widehat{CSO}=180^{\circ}$

Ainsi,

$\widehat{COS}=180^{\circ}-75^{\circ}-55^{\circ}=50^{\circ}$

$S\$ et

$\ R$ étant les projetés orthogonaux respectifs de

$F\$ et

$\ E$ sur

$(OS)$ alors, les triangles

$FOS\$ et

$\ ERO$ sont rectangles respectivement en

$S\$ et

$\ R.$

Ainsi, on a :

$\cos\widehat{EOR}=\dfrac{OR}{OE}\ \Rightarrow\ OR=OE\times\cos\widehat{EOR}$

$\cos\widehat{FOS}=\dfrac{OS}{OF}\ \Rightarrow\ OS=OF\times\cos\widehat{FOS}$

Or,

$\cos\widehat{EOR}=\cos\widehat{FOS}=\cos 50^{\circ}$

Par ailleurs, on sait que :

$RS=OS-OR.$

Alors, en remplaçant

$OS\$ et

$\ OR$ par leur expression, on trouve :

$\begin{array}{rcl} RS&=&OS-OR\\\\&=&OF\times\cos\widehat{FOS}-OE\times\cos\widehat{EOR}\\\\&=&OF\times\cos 50^{\circ}-OE\times\cos 50^{\circ}\\\\&=&\cos 50^{\circ}\times(OF-OE)\\\\&=&\cos 50^{\circ}\times EF\end{array}$

Donc,

$\boxed{RS=EF\times\cos 50^{\circ}}$

Or,

$EF=8\;cm\$ et

$\ \cos 50^{\circ}=0.6427$

Par suite,

$\begin{array}{rcl} RS&=&EF\times\cos 50^{\circ}\\\\&=&8\times 0.6427\\\\&=&5.1416\end{array}$

D'où, en arrondissant au dixième près, on trouve :

$\boxed{RS\simeq 5.1\;cm}$

Sur le dessin, en mesurant les longueurs

$IJ\$ et

$\ RS$ , on trouve :

$IJ=2.07\;cm$

$RS=5.14\;cm$

Ce qui vérifie bien les résultats trouvés.

Exercice 10

$OAB$ est un triangle,

$OA=\sqrt{10}\;;\ OB=3\sqrt{10}\$ et

$\ AB=10\;cm.$

Déterminons la nature de

$OAB.$

Pour cela, calculons les carrés des longueurs des côtés du triangle

$OAB.$

On a :

$AB^{2}=10^{2}=100$

$OA^{2}=(\sqrt{10})^{2}=10$

$OB^{2}=(3\sqrt{10})^{2}=9\times 10=90$

Alors,

$OA^{2}+OB^{2}=10+90=100$

Nous constatons que

$OA^{2}+OB^{2}=AB^{2}$

Donc, d'après la réciproque du théorème de Pythagore, le triangle

$OAB$ est rectangle en

$O.$

2) Calculons le cosinus de l'angle

$\widehat{OBA}.$

Le triangle

$OAB$ étant rectangle en

$O$ alors, le cosinus de l'angle

$\widehat{OBA}$ est donné par :

$\cos\widehat{OBA}=\dfrac{OB}{AB}$

En remplaçant

$OB\$ et

$\ AB$ par leur valeur, on obtient :

$\begin{array}{rcl} \cos\widehat{OBA}&=&\dfrac{OB}{AB}\\\\&=&\dfrac{3\sqrt{10}}{10}\end{array}$

D'où,

$\boxed{\cos\widehat{OBA}=\dfrac{3\sqrt{10}}{10}}$

En déduisons

$\sin\widehat{OBA}$

On sait que :

$\cos^{2}\widehat{OBA}+\sin^{2}\widehat{OBA}=1$

Ce qui entraine :

$\sin^{2}\widehat{OBA}=1-\cos^{2}\widehat{OBA}$

Ainsi,

$\sin\widehat{OBA}=\sqrt{1-\cos^{2}\widehat{OBA}}$

Donc, en remplaçant

$\cos\widehat{OBA}$ par sa valeur, on obtient :

$\begin{array}{rcl} \sin\widehat{OBA}&=&\sqrt{1-\cos^{2}\widehat{OBA}}\\\\&=&\sqrt{1-\left(\dfrac{3\sqrt{10}}{10}\right)^{2}}\\\\&=&\sqrt{1-\dfrac{90}{100}}\\\\&=&\sqrt{\dfrac{100}{100}-\dfrac{90}{100}}\\\\&=&\sqrt{\dfrac{10}{100}}\\\\&=&\dfrac{\sqrt{10}}{\sqrt{100}}\\\\&=&\dfrac{\sqrt{10}}{10}\end{array}$

D'où,

$\boxed{\sin\widehat{OBA}=\dfrac{\sqrt{10}}{10}}$

3) Sachant que

$3.162<\sqrt{10}<3.163$ donnons la valeur approchée par défaut à l'ordre

$4$ de

$\cos\widehat{OBA}.$

Pour cela, encadrons d'abord

$\cos\widehat{OBA}.$

On a :

$3.162<\sqrt{10}<3.163$

Alors, en multipliant chaque membre de cette inégalité par

$3$ , on obtient :

$3\times 3.162<3\times\sqrt{10}<3\times 3.163$

Ce qui donne :

$9.486<3\sqrt{10}<9.489$

En divisant chaque membre de cette inégalité par

$10$ , on trouve :

$\dfrac{9.486}{10}<\dfrac{3\sqrt{10}}{10}<\dfrac{9.489}{10}$

Ce qui est équivalent à :

$0.9486<\dfrac{3\sqrt{10}}{10}<0.9489$

Ainsi, un encadrement à l'ordre

$4$ de

$\cos\widehat{OBA}$ est donné par :

$\boxed{0.9486<\cos\widehat{OBA}<0.9489}$

D'où, une valeur approchée par défaut à l'ordre

$4$ de

$\cos\widehat{OBA}$ est égale à :

$0.9486$

En déduisons la valeur approchée à

$1$ degré près de

$\widehat{OBA}.$

On donne :

$\cos 17^{\circ}\approx 0.9543\;,\ \cos 18^{\circ}\approx 0.9511\;,\ \cos 19^{\circ}\approx 0.9455\$ et

$\ \cos 20^{\circ}\approx 0.9397$

D'après les données,

$\cos 19^{\circ}$ est plus proche de la valeur approchée par défaut à l'ordre

$4$ de

$\cos\widehat{OBA}.$

Par conséquent, la valeur approchée à

$1$ degré près de

$\widehat{OBA}$ est égale à :

$19^{\circ}.$

Exercice 11

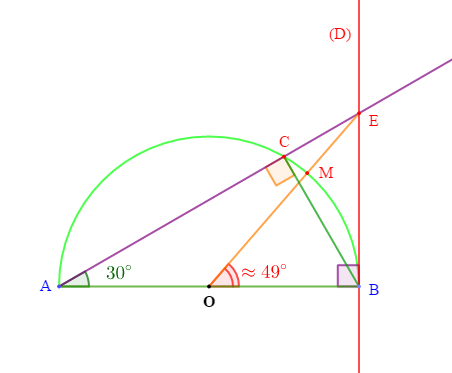
Soit un demi-cercle de centre

$O$ et de diamètre

$[AB]$ tel que

$AB=6\;cm.$

Traçons la droite

$(D)$ perpendiculaire à

$(AB)$ passant par

$B$ et marquons un point

$C$ sur le demi-cercle tel que l'angle

$\widehat{CAB}=30^{o}.$

Par ailleurs, la demi droite

$[AC)$ coupe la droite

$(D)$ en

$E.$

1) Donnons la nature des triangles

$ABC\$ et

$\ AEB$ en justifiant.

$ABC\$ et

$\ AEB$ sont des triangles rectangles respectivement en

$C\$ et

$\ B$

En effet, les points

$A\;;\ B\$ et

$\ C$ appartiennent tous à un même demi-cercle.

Or,

$[AB]$ est un diamètre pour ce demi-cercle.

Donc, le triangle

$ABC$ est rectangle en

$C.$

Par ailleurs, la droite

$(D)$ étant perpendiculaire à la droite

$(AB)$ au point

$B$ alors,

$mes\;\widehat{ABE}=90^{\circ}.$

D'où, le triangle

$AEB$ est rectangle en

$B.$

2) Calculons

$AC\;,\ BC\;,\ AE$ et

$EB.$

$-\ \$ Calcul de

$AC$

$ABC$ rectangle en

$C$ et

$mes\;\widehat{CAB}=30^{\circ}$ alors :

$\cos\widehat{CAB}=\dfrac{AC}{AB}$

Or,

$\cos\widehat{CAB}=\cos 30^{\circ}=\dfrac{\sqrt{3}}{2}$

Donc,

$\dfrac{AC}{AB}=\dfrac{\sqrt{3}}{2}$

Par suite,

$AC=\dfrac{\sqrt{3}\times AB}{2}=\dfrac{6\sqrt{3}}{2}$

D'où,

$\boxed{AC=3\sqrt{3}\;cm}$

$-\ \$ Calcul de

$BC$

De la même manière, on peut remarquer que :

$\sin\widehat{CAB}=\dfrac{BC}{AB}$

Or,

$\sin\widehat{CAB}=\sin 30^{\circ}=\dfrac{1}{2}$

Donc,

$\dfrac{BC}{AB}=\dfrac{1}{2}$

Par suite,

$BC=\dfrac{AB}{2}=\dfrac{6}{2}$

D'où,

$\boxed{BC=3\;cm}$

$-\ \$ Calcul de

$AE$

Le triangle

$AEB$ étant rectangle en

$B$ alors :

$\cos\widehat{EAB}=\dfrac{AB}{AE}$

Or,

$\cos\widehat{EAB}=\cos 30^{\circ}=\dfrac{\sqrt{3}}{2}$

Donc,

$\dfrac{AB}{AE}=\dfrac{\sqrt{3}}{2}$

Ainsi,

$2\times AB=AE\times\sqrt{3}$

Par suite,

$AE=\dfrac{2\times AB}{\sqrt{3}}=\dfrac{12}{\sqrt{3}}$

D'où, en rendant rationnel le dénominateur et en simplifiant par 3, on obtient :

$\boxed{AE=4\sqrt{3}\;cm}$

$-\ \$ Calcul de

$EB$

En considérant le sinus de l'angle

$\widehat{EAB}$ , on obtient :

$\sin\widehat{EAB}=\dfrac{EB}{AE}$

Comme

$\sin\widehat{EAB}=\sin 30^{\circ}=\dfrac{1}{2}$ alors,

$\dfrac{EB}{AE}=\dfrac{1}{2}$

Par suite,

$EB=\dfrac{AE}{2}=\dfrac{4\sqrt{3}}{2}$

D'où,

$\boxed{EB=2\sqrt{3}\;cm}$

3) Sur l'arc

$\overset{\displaystyle\frown}{BC}$ , marquons le point

$M$ tel que les points

$O\;,\ M\$ et

$\ E$ soient alignés.

a) Calculons le cosinus de l'angle

$\widehat{MOB}$

$O\;,\ M\$ et

$\ E$ étant alignés alors, le cosinus de l'angle

$\widehat{MOB}$ peut être calculé en considérant le triangle

$EOB$ rectangle en

$B.$

On a :

$\cos\widehat{MOB}=\dfrac{OB}{OE}$

Or,

$OB=\dfrac{AB}{2}\$ car

$O$ est milieu de

$[AB]$ et

$OE^{2}=OB^{2}+EB^{2}$ d'après le théorème de Pythagore.

Donc,

$\begin{array}{rcl} OE&=&\sqrt{OB^{2}+EB^{2}}\\ \\&=&\sqrt{(3^{2})+(2\sqrt{3})^{2}}\\ \\&=&\sqrt{9+12}\\ \\&=&\sqrt{21}\end{array}$

Par suite,

$\begin{array}{rcl}\cos\widehat{MOB}&=&\dfrac{OB}{OE}\\\\&=&\dfrac{3}{\sqrt{21}}\\ \\&=&\dfrac{3\sqrt{21}}{21}\\ \\&=&\dfrac{\sqrt{21}}{7}\end{array}$

D'où,

$\boxed{\cos\widehat{MOB}=\dfrac{\sqrt{21}}{7}}$

b) Donnons sa valeur approchée par défaut à

$10^{-3}$ près sachant que

$4.582\leq\sqrt{21}\leq 4.583$

On a :

$\begin{array}{rcrcccl} 4.582\leq \sqrt{21}\leq 4.583&\Rightarrow&\dfrac{4.582}{7}&\leq&\dfrac{\sqrt{21}}{7}&\leq&\dfrac{4.583}{7}\\ \\&\Rightarrow&0.65457&\leq&\dfrac{\sqrt{21}}{7}&\leq&0.654714 \\ \\&\Rightarrow&0.654&\leq&\dfrac{\sqrt{21}}{7}&\leq&0.655 \\ \\&\Rightarrow&0.654&\leq&\cos\widehat{MOB}&\leq&0.655 \end{array}$

Ainsi,

$0.654$ est une valeur approchée par défaut de

$\cos\widehat{MOB}$ à

$10^{-3}$ près.

c) Déduisons la mesure de l'angle

$\widehat{EOB}$ à un degré près par défaut.

On a :

$0.654\leq\cos\widehat{MOB}\leq 0.655$

Donc,

$49^{\circ}\leq\widehat{MOB}\leq 50^{\circ}$

Par suite,

$\boxed{\widehat{EOB}=49^{\circ}}$

Exercice 12

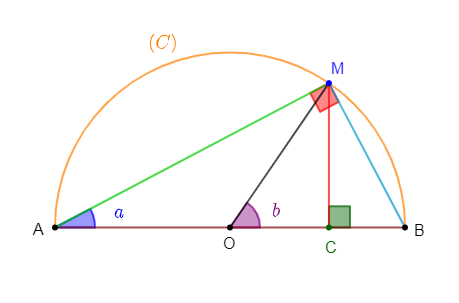
1) Traçons un demi-cercle

$(C)$ de centre

$O$ et de diamètre

$[AB]$ tel que

$AB=2r.$ Soit

$M$ un point du demi-cercle

$(C)$ plus proche de

$B$ que de

$A.$

Le triangle

$AMB$ est rectangle en

$M.$

Justifions.

En effet,

$AMB$ est un triangle inscrit dans le demi-cercle

$(C)$ et dont le côté

$[AB]$ est le diamètre de ce demi-cercle.

Par conséquent,

$AMB$ est rectangle en

$M.$

2) Soit

$a\$ et

$\ b$ les mesures respectives en degrés des angles

$\widehat{BAM}\$ et

$\ \widehat{BOM}\$ et

$\ C$ le pied de la hauteur du triangle

$AMB$ issue de

$M.$

a) Donnons deux expressions différentes de

$\cos a.$

En considérant le triangle

$AMB$ rectangle en

$M$ , on a :

$\cos a=\dfrac{AM}{AB}\qquad(\text{égalité 1})$

Par ailleurs, comme

$C$ le pied de la hauteur du triangle

$AMB$ issue de

$M$ alors, le triangle

$AMC$ est rectangle en

$C.$

Ainsi,

$\cos a$ est donné par :

$\cos a=\dfrac{AC}{AM}\qquad(\text{égalité 2})$

b) En déduisons que :

$AC=AM\cos a\;,\ AM^{2}=AB\times AC$

D'après l'égalité

$(2)$ , on a :

$\cos a=\dfrac{AC}{AM}$

Ce qui entraine :

$AC=AM\times\cos a$

D'où,

$\boxed{AC=AM\cos a}$

Par ailleurs, en comparant les égalités

$(1)\$ et

$\ (2)$ , on obtient :

$\dfrac{AM}{AB}=\dfrac{AC}{AM}$

Ce qui entraine :

$AM\times AM=AB\times AC$

Ainsi,

$\boxed{AM^{2}=AB\times AC}$

c) On sait que

$AC=AO+OC$ : Exprimons

$OC$ en fonction de

$\cos b.$

Le triangle

$MOC$ étant rectangle en

$C$ alors, on a :

$\cos b=\dfrac{OC}{OM}$

Ce qui entraine :

$OC=OM\times\cos b$

Comme

$OM=r$ alors, on trouve :

$\boxed{OC=r\times\cos b}$

En déduisons que

$AC=r(1+\cos b)$

Comme

$AC=AO+OC$ alors, remplaçons

$AO\$ et

$\ OC$ par leur valeur.

On a :

$\begin{array}{rcl} AC&=&AO+OC\\\\&=&r+r\cos b\\\\&=&r(1+\cos b)\end{array}$

Donc,

$\boxed{AC=r(1+\cos b)}$

d) Déduisons des questions précédentes que :

$\cos^{2}a=\dfrac{1+\cos b}{2}$

D'après l'égalité

$(2)$ , on a :

$\cos a=\dfrac{AC}{AM}$

Donc,

$\cos^{2} a=\left(\dfrac{AC}{AM}\right)^{2}=\dfrac{AC^{2}}{AM^{2}}$

Or, d'après le résultat de la question

$2)\,b)$ , on a :

$AM^{2}=AB\times AC$

Alors, en remplaçant

$AM^{2}$ par

$AB\times AC$ , on obtient :

$\cos^{2} a=\dfrac{AC^{2}}{AM^{2}}=\dfrac{AC^{2}}{AB\times AC}=\dfrac{AC}{AB}$

Ainsi, en remplaçant

$AC\$ et

$\ AB$ par leur expression, on trouve :

$\begin{array}{rcl} \cos^{2} a&=&\dfrac{AC}{AB}\\\\&=&\dfrac{r(1+\cos b)}{2r}\\\\&=&\dfrac{1+\cos b}{2}\end{array}$

D'où,

$\boxed{\cos^{2} a=\dfrac{1+\cos b}{2}}$

Exercice 13

$x\$ et

$\ a$ sont des angles aigus

1) Sachant que

$\cos x=\dfrac{\sqrt{5}}{3}$ , calculons

$\sin x\$ et

$\ \tan x.$

$-\$ Calcul de

$\sin x$

On sait que :

$\cos^{2}x+\sin^{2}x=1$

Ce qui entraine :

$\sin^{2}x=1-\cos^{2}x$

Ainsi,

$\sin x=\sqrt{1-\cos^{2}x}$

Donc, en remplaçant

$\cos x$ par sa valeur

$\dfrac{\sqrt{5}}{3}$ , on obtient :

$\begin{array}{rcl} \sin x&=&\sqrt{1-\cos^{2}x}\\\\&=&\sqrt{1-\left(\dfrac{\sqrt{5}}{3}\right)^{2}}\\\\&=&\sqrt{1-\dfrac{5}{9}}\\\\&=&\sqrt{\dfrac{9}{9}-\dfrac{5}{9}}\\\\&=&\sqrt{\dfrac{4}{9}}\\\\&=&\dfrac{\sqrt{4}}{\sqrt{9}}\\\\&=&\dfrac{2}{3}\end{array}$

D'où,

$\boxed{\sin x=\dfrac{2}{3}}$

$-\$ Calcul de

$\tan x$

On a :

$\tan x=\dfrac{\sin x}{\cos x}$

Alors, en remplaçant

$\sin x\$ et

$\ \cos x$ par leur valeur, on trouve :

$\begin{array}{rcl} \tan x&=&\dfrac{\sin x}{\cos x}\\\\&=&\dfrac{\dfrac{2}{3}}{\dfrac{\sqrt{5}}{3}}\\\\&=&\dfrac{2}{3}\times\dfrac{3}{\sqrt{5}}\\\\&=&\dfrac{2}{\sqrt{5}}\\\\&=&\dfrac{2\sqrt{5}}{5}\end{array}$

Donc,

$\boxed{\tan x=\dfrac{2\sqrt{5}}{5}}$

2) Soit l'expression

$F(a)=(1-\cos a)(1+\cos a)(1+\tan^{2}a)$

a) Démontrons que

$F(a)=\tan^{2}a$

Dans l'écriture de

$F(a)$ , on identifie une identité remarquable :

$(1-\cos a)(1+\cos a)=(1-\cos^{2} a)$

Or, on sait que :

$\cos^{2} a+\sin^{2} a=1$

Ce qui entraine :

$(1-\cos^{2} a)=\sin^{2} a$

Donc, en remplaçant

$(1-\cos a)(1+\cos a)$ par

$\sin^{2} a$ , on trouve :

$\begin{array}{rcl} F(a)&=&(1-\cos a)(1+\cos a)(1+\tan^{2}a)\\\\&=&\sin^{2} a\left(1+\dfrac{\sin^{2}a}{\cos^{2}a}\right)\\\\&=&\sin^{2} a\left(\dfrac{\cos^{2}a}{\cos^{2}a}+\dfrac{\sin^{2}a}{\cos^{2}a}\right)\\\\&=&\sin^{2} a\left(\dfrac{\cos^{2}a+\sin^{2}a}{\cos^{2}a}\right)\\\\&=&\sin^{2} a\times\dfrac{1}{\cos^{2}a}\\\\&=&\dfrac{\sin^{2}a}{\cos^{2}a}\\\\&=&\left(\dfrac{\sin a}{\cos a}\right)^{2}\\\\&=&\tan^{2}a\end{array}$

D'où,

$\boxed{F(a)=\tan^{2}a}$

b) Calculons

$F(30^{\circ})$

En utilisant le résultat de la question

$2)\,a)$ , on a :

$F(30^{\circ})=\tan^{2}30^{\circ}=\left(\dfrac{\sin 30^{\circ}}{\cos 30^{\circ}}\right)^{2}$

Or,

$\sin 30^{\circ}=\dfrac{1}{2}\$ et

$\ \cos 30^{\circ}=\dfrac{\sqrt{3}}{2}$

Donc, en remplaçant

$\sin 30^{\circ}\$ et

$\ \cos 30^{\circ}$ par leur valeur, on obtient :

$\begin{array}{rcl} F(30^{\circ})&=&\left(\dfrac{\sin 30^{\circ}}{\cos 30^{\circ}}\right)^{2}\\\\&=&\left(\dfrac{\dfrac{1}{2}}{\dfrac{\sqrt{3}}{2}}\right)^{2}\\\\&=&\left(\dfrac{1}{2}\times\dfrac{2}{\sqrt{3}}\right)^{2}\\\\&=&\left(\dfrac{1}{\sqrt{3}}\right)^{2}\\\\&=&\dfrac{1}{3}\end{array}$

D'où,

$\boxed{F(30^{\circ})=\dfrac{1}{3}}$

3) Soit un triangle quelconque

$ABC\;;\ H$ le pied de la hauteur issue de

$A.$

Démontrons que :

$\dfrac{\sin\widehat{B}}{AC}=\dfrac{\sin\widehat{C}}{AB}.$

On a :

$\dfrac{\sin\widehat{B}}{AC}=\dfrac{\sin\widehat{C}}{AB}$ si, et seulement si,

$\sin\widehat{B}\times AB=\sin\widehat{C}\times AB$

Donc, démonter que

$\dfrac{\sin\widehat{B}}{AC}=\dfrac{\sin\widehat{C}}{AB}$ revient à démontrer que :

$\sin\widehat{B}\times AB=\sin\widehat{C}\times AB$

En effet, comme

$H$ est le pied de la hauteur issue de

$A$ alors, les triangles

$ABH\$ et

$\ ACH$ sont rectangles en

$H.$

Donc, on a :

$\sin\widehat{B}=\dfrac{AH}{AB}\ \Rightarrow\ \sin\widehat{B}\times AB=AH$

$\sin\widehat{C}=\dfrac{AH}{AC}\ \Rightarrow\ \sin\widehat{C}\times AC=AH$

Ainsi, on obtient :

$\sin\widehat{B}\times AB=\sin\widehat{C}\times AC$

Ce qui montre que :

$\boxed{\dfrac{\sin\widehat{B}}{AC}=\dfrac{\sin\widehat{C}}{AB}}$

Exercice 14

1) Sachant que

$\sin 15^{\circ}=\dfrac{\sqrt{6}-\sqrt{2}}{4}$ , vérifions que

$\cos 15^{\circ}=\dfrac{\sqrt{6}+\sqrt{2}}{4}$ puis, donnons la valeur exacte de

$\tan 15^{\circ}.$

En effet, on sait que, pour tout angle aigu

$x$ , on a :

$\cos^{2}x+\sin^{2}x=1$

Ce qui entraine :

$\cos^{2}x=1-\sin^{2}x$

Par suite,

$\cos x=\sqrt{1-\sin^{2}x}$

Donc, pour

$x=15^{\circ}$ , on trouve :

$\begin{array}{rcl} \cos 15^{\circ}&=&\sqrt{1-\sin^{2}15^{\circ}}\\\\&=&\sqrt{1-\left(\dfrac{\sqrt{6}-\sqrt{2}}{4}\right)^{2}}\\\\&=&\sqrt{1-\dfrac{6-2\sqrt{12}+2}{16}}\\\\&=&\sqrt{\dfrac{16}{16}-\dfrac{8-2\sqrt{12}}{16}}\\\\&=&\sqrt{\dfrac{16-8+2\sqrt{12}}{16}}\\\\&=&\sqrt{\dfrac{8+2\sqrt{12}}{16}}\\\\&=&\sqrt{\left(\dfrac{\sqrt{6}+\sqrt{2}}{4}\right)^{2}}\\\\&=&\left|\dfrac{\sqrt{6}+\sqrt{2}}{4}\right|\\\\&=&\dfrac{\sqrt{6}+\sqrt{2}}{4}\end{array}$

Ce qui vérifie bien que :

$\boxed{\cos 15^{\circ}=\dfrac{\sqrt{6}+\sqrt{2}}{4}}$

On a :

$\tan 15^{\circ}=\dfrac{\sin 15^{\circ}}{\cos 15^{\circ}}$

Donc, en remplaçant

$\sin 15^{\circ}\$ et

$\ \cos 15^{\circ}$ par leur valeur, on obtient :

$\begin{array}{rcl} \tan 15^{\circ}&=&\dfrac{\sin 15^{\circ}}{\cos 15^{\circ}}\\\\&=&\dfrac{\dfrac{\sqrt{6}-\sqrt{2}}{4}}{\dfrac{\sqrt{6}+\sqrt{2}}{4}}\\\\&=&\dfrac{\sqrt{6}-\sqrt{2}}{4}\times\dfrac{4}{\sqrt{6}+\sqrt{2}}\\\\&=&\dfrac{\sqrt{6}-\sqrt{2}}{\sqrt{6}+\sqrt{2}}\\\\&=&\dfrac{(\sqrt{6}-\sqrt{2})(\sqrt{6}-\sqrt{2})}{(\sqrt{6}+\sqrt{2})(\sqrt{6}-\sqrt{2})}\\\\&=&\dfrac{6-\sqrt{12}-\sqrt{12}+2}{(\sqrt{6})^{2}-(\sqrt{2})^{2}}\\\\&=&\dfrac{8-2\sqrt{12}}{6-2}\\\\&=&\dfrac{8-2\sqrt{4\times 3}}{4}\\\\&=&\dfrac{8-4\sqrt{3}}{4}\\\\&=&2-\sqrt{3}\end{array}$

Ainsi,

$\boxed{\tan 15^{\circ}=2-\sqrt{3}}$

$x\in\;]0^{\circ}\;;\ 90^{\circ}[$

a) Établissons les égalités suivantes :

Établissons l'égalité :

$1+\tan^{2}x=\dfrac{1}{\cos^{2}x}$

Soit :

$\tan x=\dfrac{\sin x}{\cos x}$

Donc,

$\tan^{2}x=\dfrac{\sin^{2}x}{\cos^{2}x}$

Par suite,

$\begin{array}{rcl} 1+\tan^{2}x&=&1+\dfrac{\sin^{2}x}{\cos^{2}x}\\\\&=&\dfrac{\cos^{2}x}{\cos^{2}x}+\dfrac{\sin^{2}x}{\cos^{2}x}\\\\&=&\dfrac{\cos^{2}x+\sin^{2}x}{\cos^{2}x}\end{array}$

Ainsi,

$1+\tan^{2}x=\dfrac{\cos^{2}x+\sin^{2}x}{\cos^{2}x}$

Or,

$\cos^{2}x+\sin^{2}x=1$

Par conséquent,

$\boxed{1+\tan^{2}x=\dfrac{1}{\cos^{2}x}}$

Établissons l'égalité :

$1-2\sin^{2}x=2\cos^{2}x-1$

On a :

$\sin^{2}x+\cos^{2}x=1$

Donc,

$\sin^{2}x=1-\cos^{2}x$

Alors, en remplaçant

$\sin^{2}x$ par

$1-\cos^{2}x$ , on obtient :

$\begin{array}{rcl} 1-2\sin^{2}x&=&1-2(1-\cos^{2}x)\\\\&=&1-2+2\cos^{2}x\\\\&=&-1+2\cos^{2}x\end{array}$

D'où,

$\boxed{1-2\sin^{2}x=2\cos^{2}x-1}$

Établissons l'égalité :

$(\cos x+\sin x)(\cos x-\sin x)=2\cos^{2}x-1$

En utilisant la forme développée des identités remarquables, on a :

$(\cos x+\sin x)(\cos x-\sin x)=2\cos^{2}x=\cos^{2}x-\sin^{2}x$

Or, on sait que :

$\sin^{2}x=1-\cos^{2}x$

Donc, en remplaçant, on trouve :

$\begin{array}{rcl} (\cos x+\sin x)(\cos x-\sin x)&=&\cos^{2}x-\sin^{2}x\\\\&=&\cos^{2}x-(1-\cos^{2}x)\\\\&=&\cos^{2}x-1+\cos^{2}x\\\\&=&2\cos^{2}x-1\end{array}$

D'où,

$\boxed{(\cos x+\sin x)(\cos x-\sin x)=2\cos^{2}x-1}$

Établissons l'égalité :

$1+\dfrac{1}{\tan^{2}x}=\dfrac{1}{\sin^{2}x}$

On a :

$\tan^{2}x=\dfrac{\sin^{2}x}{\cos^{2}x}$

Donc,

$\dfrac{1}{\tan^{2}x}=\dfrac{1}{\dfrac{\sin^{2}x}{\cos^{2}x}}=\dfrac{\cos^{2}x}{\sin^{2}x}$

Ainsi,

$\begin{array}{rcl} 1+\dfrac{1}{\tan^{2}x}&=&1+\dfrac{\cos^{2}x}{\sin^{2}x}\\\\&=&\dfrac{\sin^{2}x}{\sin^{2}x}+\dfrac{\cos^{2}x}{\sin^{2}x}\\\\&=&\dfrac{\sin^{2}x+\cos^{2}x}{\sin^{2}x}\\\\&=&\dfrac{1}{\sin^{2}x}\end{array}$

D'où,

$\boxed{1+\dfrac{1}{\tan^{2}x}=\dfrac{1}{\sin^{2}x}}$

b) Simplifions

$\sqrt{1-\cos x}\times\sqrt{1+\cos x}\$ et

$\ \sqrt{1+\tan^{2}x}$

On a :

$\begin{array}{rcl} \sqrt{1-\cos x}\times\sqrt{1+\cos x}&=&\sqrt{(1-\cos x)(1+\cos x)}\\\\&=&\sqrt{1^{2}-\cos^{2}x}\\\\&=&\sqrt{1-\cos^{2}x}\\\\&=&\sqrt{\sin^{2}x}\\\\&=&|\sin x|\end{array}$

Or,

$x\in\;]0^{\circ}\;;\ 90^{\circ}[$ donc,

$\sin x>0$

Par suite,

$|\sin x|=\sin x$

Ainsi,

$\boxed{\sqrt{1-\cos x}\times\sqrt{1+\cos x}=\sin x}$

D'après les résultats de la question

$a)$ , on a :

$1+\tan^{2}x=\dfrac{1}{\cos^{2}x}$

Donc,

$\begin{array}{rcl} \sqrt{1+\tan^{2}x}&=&\sqrt{\dfrac{1}{\cos^{2}x}}\\\\&=&\dfrac{\sqrt{1}}{\sqrt{\cos^{2}x}}\\\\&=&\dfrac{1}{|\cos x|}\end{array}$

Comme

$x\in\;]0^{\circ}\;;\ 90^{\circ}[$ alors,

$\cos x>0$

D'où,

$|\cos x|=\cos x$

Par conséquent,

$\boxed{\sqrt{1+\tan^{2}x}=\dfrac{1}{\cos x}}$

Exercice 15

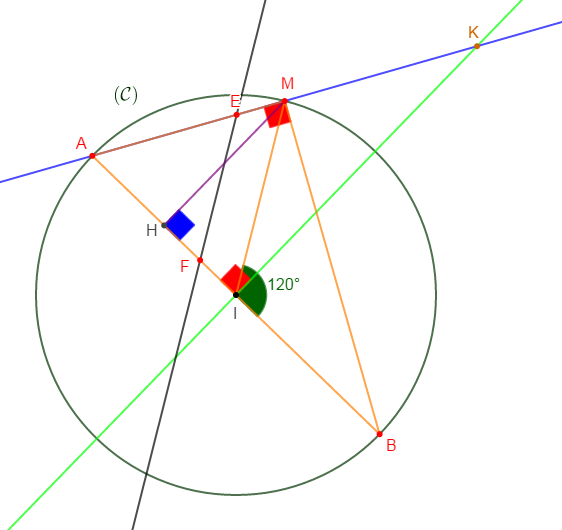
1) a) Construisons un cercle

$(\mathcal{C})$ de centre

$I$ et de rayon

$4\;cm.$ Soit

$A\$ et

$\ B$ deux points diamétralement opposés.

Plaçons un point

$M$ sur

$(\mathcal{C})$ tel que :

$AM=4\;cm.$

$AMI$ est un triangle équilatérale

En effet,

$A\$ et

$\ M$ appartiennent au cercle

$(\mathcal{C})$ donc,

$IA=IM=4\;cm$

Comme

$AM=4\;cm$ alors,

$AM=IA=IM$

Par conséquent,

$AMI$ est un triangle équilatérale.

c) En déduisons la mesure de l'angle

$\widehat{BIM}.$

On sait que les angles

$\widehat{BIM}\$ et

$\ \widehat{BIM}$ sont supplémentaires donc,

$mes\,\widehat{BIM}+mes\,\widehat{MIA}=180^{\circ}$

Or,

$AMI$ est équilatérale donc,

$mes\,\widehat{MIA}=mes\,\widehat{IAM}=mes\,\widehat{AMI}=60^{\circ}$

Par suite,

$\begin{array}{rcl} mes\,\widehat{BIM}+mes\,\widehat{MIA}=180^{\circ}&\Rightarrow&mes\,\widehat{BIM}=180^{\circ}-mes\,\widehat{MIA}\\ \\&\Rightarrow&mes\,\widehat{BIM}=180^{\circ}-60^{\circ}\\\\&\Rightarrow&mes\,\widehat{BIM}=120^{\circ}\end{array}$

Ainsi,

$\boxed{mes\,\widehat{BIM}=120^{\circ}}$

$K$ est le point d'intersection de la perpendiculaire à

$(AB)$ passant par

$I$ et la droite

$(AM).$

a) Justifions que

$AMB$ est un triangle rectangle.

$A\;,\ B\$ et

$\ M$ sont trois points du cercle

$(\mathcal{C}).$

Or,

$[AB]$ est un diamètre donc,

$AMB$ est un triangle rectangle en

$M.$

b) En remarquant que

$\cos\widehat{BAM}=\cos\widehat{KAI}.$

Calculons

$AK\$ et

$\ KI.$

$-\$ Calcul de

$AK$

On a :

$\cos\widehat{BAM}=\dfrac{AM}{AB}\$ et

$\ \cos\widehat{KAI}=\dfrac{AI}{AK}$

Comme

$\cos\widehat{BAM}=\cos\widehat{KAI}$ alors,

$\begin{array}{rcl}\dfrac{AM}{AB}= \dfrac{AI}{AK}&\Rightarrow&AK\times AM=AB\times AI\\\\&\Rightarrow&AK=\dfrac{AB\times AI}{AM}\\\\&\Rightarrow&AK=\dfrac{8\times 4}{4}\\\\&\Rightarrow&AK=8\end{array}$

Donc,

$\boxed{AK=8\;cm}$

$-\$ Calcul de

$KI$

$KAI$ étant rectangle en

$I$ alors, en appliquant le théorème de Pythagore, on obtient :

$\begin{array}{rcl} KI^{2}+AI^{2}=AK^{2}&\Rightarrow&KI^{2}=AK^{2}-AI^{2}\\\\&\Rightarrow&KI=\sqrt{AK^{2}-AI^{2}}\\\\&\Rightarrow&KI=\sqrt{8^{2}-4^{2}}\\\\&\Rightarrow&KI=\sqrt{64-16}\\\\&\Rightarrow&KI=\sqrt{48}\\\\&\Rightarrow&KI=4\sqrt{3}\end{array}$

Ainsi,

$\boxed{KI=4\sqrt{3}\;cm}$

3) Le point

$H$ est le projeté de

$M$ sur

$(AB).$

a) Calculons

$\cos\widehat{B}$ de deux manières différentes.

On a :

$\left\lbrace\begin{array}{rcl}\cos\widehat{B}&=&\dfrac{BM}{AB}\\ \\\cos\widehat{B}&=&\dfrac{BH}{BM}\end{array}\right.$

b) Exprimons

$BH$ en fonction de

$\cos\widehat{B}$

On a :

$\begin{array}{rcl}\cos\widehat{B}=\dfrac{BH}{BM}&\Rightarrow&BH=\cos\widehat{B}\times BM\end{array}$

Donc,

$\boxed{BH=\cos\widehat{B}\times BM}$

Démontrons que :

$BH=\dfrac{BM^{2}}{AB}$

On a :

$BH=\cos\widehat{B}\times BM$

Or,

$\cos\widehat{B}=\dfrac{BM}{AB}$ donc, en remplaçant

$\cos\widehat{B}$ par

$\dfrac{BM}{AB}$ , on obtient :

$\begin{array}{rcl} BH&=&\cos\widehat{B}\times BM\\\\&=&\dfrac{BM}{AB}\times BM\\\\&=&\dfrac{BM\times BM}{AB}\\\\&=&\dfrac{BM^{2}}{AB}\end{array}$

D'où,

$\boxed{BH=\dfrac{BM^{2}}{AB}}$

4) Plaçons le point

$E$ sur le segment

$[AM]$ tel que :

$AE=3\;cm.$

La parallèle à

$(IM)$ passant par

$E$ coupe

$[AI]$ en

$F.$

Le triangle

$AEF$ est équilatérale.

En effet, les triangles

$AEF\$ et

$\ AMI$ sont en position de Thalès de sommet commun

$A.$

Donc, en appliquant le théorème de Thalès, on obtient :

$\dfrac{AE}{AM}=\dfrac{AF}{AI}=\dfrac{EF}{IM}$

Par suite,

$\begin{array}{rcl}\dfrac{AE}{AM}=\dfrac{AF}{AI}&\Rightarrow&AF=\dfrac{AE\times AI}{AM}\\\\&\Rightarrow&AF=\dfrac{3\times 4}{4}\\\\&\Rightarrow&AF=3\end{array}$

Donc,

$\boxed{AF=3\;cm}$

Aussi, on a :

$\begin{array}{rcl}\dfrac{AE}{AM}=\dfrac{EF}{IM}&\Rightarrow&EF=\dfrac{AE\times IM}{AM}\\\\&\Rightarrow&EF=\dfrac{3\times 4}{4}\\\\&\Rightarrow&EF=3\end{array}$

Donc,

$\boxed{EF=3\;cm}$

Ainsi,

$AE=AF=EF$

Par conséquent, le triangle

$AEF$ est équilatérale.

Exercice 16

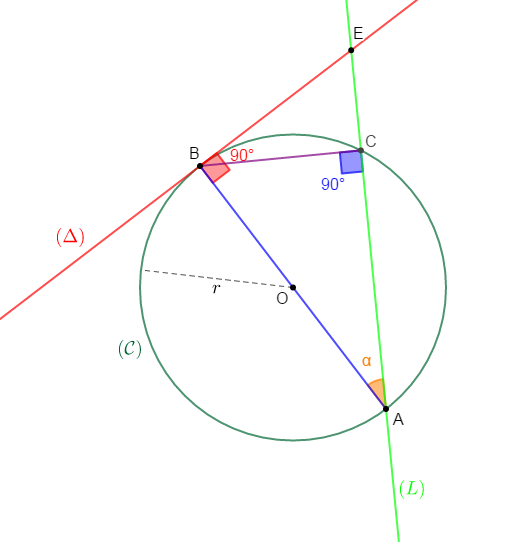
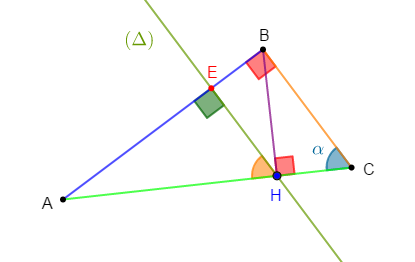
On considère un cercle

$(\mathcal{C})$ de centre

$O$ et de rayon

$r.$ Soit

$[AB]$ un diamètre de ce cercle ;

$(\Delta)$ la tangente en

$B\$ à

$\ (\mathcal{C}).$ Une droite

$(L)$ passant par

$A$ recoupe

$(\mathcal{C})\$ en

$\ C$ et recoupe

$(\Delta)\$ en

$\ E.$ On désigne par

$\alpha$ la mesure de

$\widehat{BAC}.$

1) Exprimons en fonction de

$r\$ et

$\ \alpha\ :\ CA\;;\ CB\;;\ EA\;;\ EB.$

$-\$ Expression de

$CA$

On sait que les points

$A\;,\ B\$ et

$\ C$ appartiennent au cercle

$(\mathcal{C})$ et que

$[AB]$ est un diamètre donc, le triangle

$ABC$ est rectangle en

$C.$

Ainsi,

$\cos\alpha=\dfrac{CA}{AB}$

Ce qui donne :

$CA=AB\times\cos\alpha$

Comme,

$AB=2\times r$ alors

$\boxed{CA=2\times r\times\cos\alpha}$

$-\$ Expression de

$CB$

Toujours, en considérant le triangle

$ABC$ , on a :

$\dfrac{CB}{AB}=\sin\alpha$

Donc,

$CB=AB\times\sin\alpha$ avec

$AB=2\times r$

Par suite,

$\boxed{CB=2\times r\times\sin\alpha}$

$-\$ Expression de

$EA$

On sait que

$(\Delta)$ est tangente à

$(\mathcal{C})$ au point

$B.$ Donc,

$(\Delta)$ est perpendiculaire à

$(AB).$

Par conséquent, le triangle

$ABE$ est rectangle en

$B.$

Ainsi,

$\dfrac{AB}{EA}=\cos\alpha$ avec

$AB=2\times r$

Ce qui donne :

$2\times r=EA\times\cos\alpha$

D'où,

$\boxed{EA=\dfrac{2\times r}{\cos\alpha}}$

$-\$ Expression de

$EB$

Toujours, dans ce même triangle

$ABE$ , on a :

$\dfrac{EB}{AB}=\tan\alpha$

Ce qui entraine :

$EB=AB\times\tan\alpha$

Comme

$AB=2\times r$ alors, on obtient :

$\boxed{EB=2\times r\times\tan\alpha}$

2) Calculons :

$CA\;;\ CB\;;\ EA\;;\ EB$ pour

$r=2\;cm\$ et

$\ \alpha=30^{\circ}.$

$-\$ Calcul de

$CA$

On a :

$CA=2\times r\times\cos\alpha$

Donc, pour

$r=2\;cm\$ et

$\ \alpha=30^{\circ}$ , on obtient :

$\begin{array}{rcl} CA&=&2\times r\times\cos\alpha\\\\&=&2\times 2\times\cos 30^{\circ}\\\\&=&4\times\dfrac{\sqrt{3}}{2}\\\\&=&2\sqrt{3}\end{array}$

Ainsi,

$\boxed{CA=2\sqrt{3}\;cm}$

$-\$ Calcul de

$CB$

On a :

$CB=2\times r\times\sin\alpha$

Or,

$r=2\;cm\$ et

$\ \alpha=30^{\circ}$ , donc :

$\begin{array}{rcl} CB&=&2\times r\times\sin\alpha\\\\&=&2\times 2\times\sin 30^{\circ}\\\\&=&4\times\dfrac{1}{2}\\\\&=&2\end{array}$

D'où,

$\boxed{CB=2\;cm}$

$-\$ Calcul de

$EA$

On a :

$EA=\dfrac{2\times r}{\cos\alpha}$

Donc, pour

$r=2\;cm\$ et

$\ \alpha=30^{\circ}$ , on obtient :

$\begin{array}{rcl} EA&=&\dfrac{2\times r}{\cos\alpha}\\\\&=&\dfrac{2\times 2}{\cos 30^{\circ}}\\\\&=&\dfrac{4}{\dfrac{\sqrt{3}}{2}}\\\\&=&\dfrac{4\times 2}{\sqrt{3}}\\\\&=&\dfrac{8}{\sqrt{3}}\end{array}$

Par suite,

$EA=\dfrac{8}{\sqrt{3}}$

En rendant rationnel le dénominateur, on obtient :

$\begin{array}{rcl} EA&=&\dfrac{8}{\sqrt{3}}\\\\&=&\dfrac{8\times\sqrt{3}}{\sqrt{3}\times\sqrt{3}}\\\\&=&\dfrac{8\sqrt{3}}{3}\end{array}$

Ainsi,

$\boxed{EA=\dfrac{8\sqrt{3}}{3}\;cm}$

$-\$ Calcul de

$EB$

On a :

$EB=2\times r\times\tan\alpha$

Or,

$r=2\;cm\$ et

$\ \alpha=30^{\circ}$ , donc :

$\begin{array}{rcl} EB&=&2\times r\times\tan\alpha\\\\&=&2\times 2\times\tan 30^{\circ}\\\\&=&4\times\dfrac{\sqrt{3}}{3}\\\\&=&\dfrac{4\sqrt{3}}{3}\end{array}$

D'où,

$\boxed{EB=\dfrac{4\sqrt{3}}{3}\;cm}$

Exercice 17

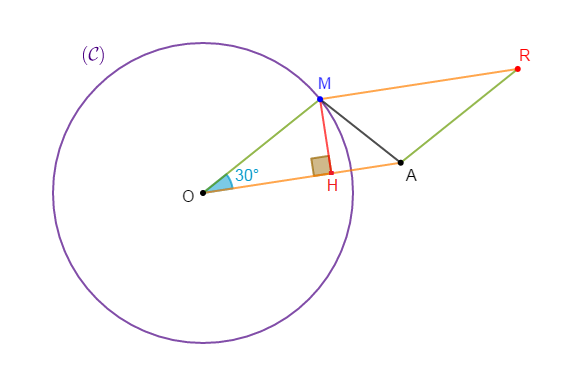
Soit un segment

$[OA]\;,\ OA=4\;cm.$

$M$ est un point appartenant au cercle

$\mathcal{C}(O\;,\ 3\;cm)$ tel que :

$\widehat{AOM}=30^{\circ}\;,\ R$ un point du plan tel que

$OARM$ est un parallélogramme.

Calculons l'aire de

$OARM.$

Pour cela, projetons orthogonalement

$M$ sur

$[AO].$

Alors,

$[MH]$ est une hauteur issue de

$M.$

Par suite,

$\text{Aire de }OARM=MH\times OA$

Déterminons alors la longueur

$MH.$

En effet,

$H$ étant le projeté orthogonal de

$M$ sur

$[OA]$ alors, le triangle

$MOH$ est rectangle en

$H.$

Ainsi,

$\dfrac{MH}{OM}=\sin 30^{\circ}$

Ce qui entraine :

$MH=OM\times\sin 30^{\circ}$

Or,

$OM=3\;cm\$ et

$\ \sin 30^{\circ}=\dfrac{1}{2}$

Donc,

$MH=3\times\dfrac{1}{2}=\dfrac{3}{2}$

Par conséquent, en remplaçant

$MH\$ et

$\ OA$ par leur valeur, on trouve :

$\begin{array}{rcl} \text{Aire de }OARM&=&MH\times OA\\\\&=&\dfrac{3}{2}\times 4\\\\&=&\dfrac{12}{2}\\\\&=&6\end{array}$

D'où,

$\boxed{\text{Aire de }OARM=6\;cm^{2}}$

Exercice 18

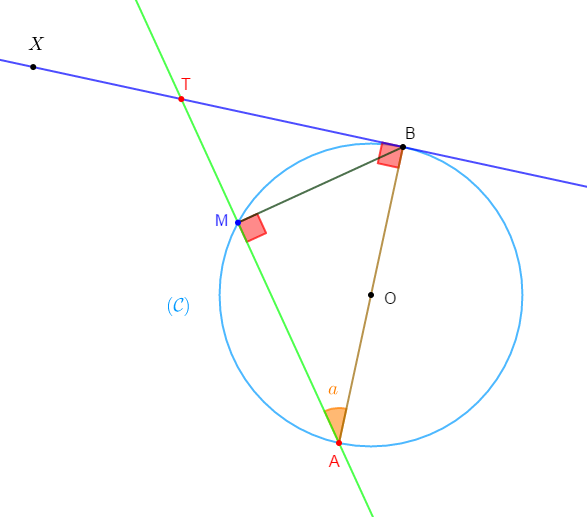
$(\mathcal{C})$ est un cercle de diamètre

$[AB]$ , de rayon

$r,\ (BX)$ est tangente à

$(\mathcal{C})$ en

$B.$

Une droite passant par

$A$ coupe

$(\mathcal{C})$ en

$M$ et la tangente

$(BX)$ en

$T$ , avec

$\widehat{BAT}=a^{\circ}.$

Exprimons

$AM\;,\ MB\;,\ BT\;,\ AT$ à l'aide de

$a\$ et

$\ r.$

En effet,

$AMB$ est un triangle inscrit dans le cercle

$(\mathcal{C})$ dont le côté

$[AB]$ est un diamètre de ce cercle.

Par conséquent, le triangle

$AMB$ est rectangle en

$M.$

D'où, le cosinus de l'angle

$\widehat{BAT}$ est donné par :

$\cos\widehat{BAT}=\dfrac{AM}{AB}$

Ce qui entraine :

$AM=AB\times\cos\widehat{BAT}$

Or,

$[AB]$ est un diamètre du

$(\mathcal{C})$ de rayon

$r$ donc,

$AB=2r$

Ainsi, en remplaçant

$\widehat{BAT}$ par

$a$ et

$AB$ par

$2r$ , on trouve :

$AM=2r\times\cos a$

D'où,

$\boxed{AM=2r\cos a}$

Pour déterminer

$MB$ on utilise le sinus de l'angle

$\widehat{BAT}.$

On a :

$\sin\widehat{BAT}=\dfrac{MB}{AB}$

Ce qui entraine :

$MB=AB\times\sin\widehat{BAT}$

En remplaçant

$AB\$ et

$\ \widehat{BAT}$ par leur valeur, on trouve :

$MB=2r\times\sin a$

D'où,

$\boxed{MB=2r\sin a}$

Comme

$(BX)$ est tangente à

$(\mathcal{C})$ en

$B$ et le point

$T$ appartient à

$(BX)$ alors,

$(BT)$ est perpendiculaire à

$(AB).$

Par conséquent,

$ABT$ est un triangle rectangle en

$B.$

Ainsi, pour déterminer

$BT$ on utilise la tangente de l'angle

$\widehat{BAT}.$

On a :

$\tan\widehat{BAT}=\dfrac{BT}{AB}$

Ce qui donne :

$BT=AB\times\tan\widehat{BAT}$

Ainsi, en remplaçant

$AB$ par

$2r\$ et

$\ \widehat{BAT}$ par

$a$ , on obtient :

$BT=2r\times\tan a$

D'où,

$\boxed{BT=2r\tan a}$

Pour déterminer

$AT$ on peut utiliser la première relation métrique dans le triangle

$ABT.$

$ABT$ étant rectangle en

$B$ alors, on a :

$AB^{2}=AM\times AT$

Donc,

$AT=\dfrac{AB^{2}}{AM}$

Ainsi, en remplaçant

$AB\$ et

$\ AM$ par leur valeur, on trouve :

$AT=\dfrac{(2r)^{2}}{2r\cos a}$

Ce qui donne :

$AT=\dfrac{4r^{2}}{2r\cos a}=\dfrac{2r}{\cos a}$

D'où,

$\boxed{AT=\dfrac{2r}{\cos a}}$

Exercice 19

Construisons le triangle

$ABC$ rectangle en

$A$ tel que

$AB=8\;cm\$ et

$\ AC=6\;cm.$

1) Calculons

$BC\;,\ \cos\widehat{ABC}\;,\ \sin\widehat{ABC}$ puis,

$\tan\widehat{ABC}.$

$-\$ Calcul de

$BC$

Comme le triangle

$ABC$ rectangle en

$A$ alors, d'après le théorème de Pythagore, on a :

$BC^{2}=AB^{2}+AC^{2}$

Ce qui entraine :

$\begin{array}{rcl} BC&=&\sqrt{AB^{2}+AC^{2}}\\\\&=&\sqrt{8^{2}+6^{2}}\\\\&=&\sqrt{64+36}\\\\&=&\sqrt{100}\\\\&=&10\end{array}$

Donc,

$\boxed{BC=10\;cm}$

$-\$ Calcul de

$\cos\widehat{ABC}$

Comme le triangle

$ABC$ rectangle en

$A$ alors, le cosinus de l'angle

$\widehat{ABC}$ est donné par :

$\cos\widehat{ABC}=\dfrac{AB}{BC}$

En remplaçant

$AB\$ et

$\ BC$ par leur valeur, on trouve :

$\begin{array}{rcl} \cos\widehat{ABC}&=&\dfrac{AB}{BC}\\\\&=&\dfrac{8}{10}\\\\&=&\dfrac{4}{5}\end{array}$

D'où,

$\boxed{\cos\widehat{ABC}=\dfrac{4}{5}}$

$-\$ Calcul de

$\cos\widehat{ABC}$

Comme le triangle

$ABC$ rectangle en

$A$ alors, le sinus de l'angle

$\widehat{ABC}$ est donné par :

$\sin\widehat{ABC}=\dfrac{AC}{BC}$

En remplaçant

$AC\$ et

$\ BC$ par leur valeur, on trouve :

$\begin{array}{rcl} \sin\widehat{ABC}&=&\dfrac{AC}{BC}\\\\&=&\dfrac{6}{10}\\\\&=&\dfrac{3}{5}\end{array}$

D'où,

$\boxed{\sin\widehat{ABC}=\dfrac{3}{5}}$

$-\$ Calcul de

$\tan\widehat{ABC}$

La tangente de l'angle

$\widehat{ABC}$ est donné par :

$\tan\widehat{ABC}=\dfrac{AC}{AB}$

En remplaçant

$AB\$ et

$\ AC$ par leur valeur, on trouve :

$\begin{array}{rcl} \tan\widehat{ABC}&=&\dfrac{AC}{AB}\\\\&=&\dfrac{6}{8}\\\\&=&\dfrac{3}{4}\end{array}$

D'où,

$\boxed{\tan\widehat{ABC}=\dfrac{3}{4}}$

2) Plaçons le point

$M$ sur le segment

$[AB]$ tel que :

$AM=\dfrac{1}{3}AB.$

3) La parallèle à

$(BC)$ passant par

$M$ coupe

$(AC)$ en

$N.$

Calculons

$AN.$

En effet,

$(MN)$ étant parallèle à

$(BC)$ alors, les triangles

$ABC\$ et

$\ AMN$ sont en position de Thalès.

Donc, les longueurs des côtés correspondants sont proportionnelles.

Or, on a :

$AM=\dfrac{1}{3}AB$

Par conséquent,

$AN=\dfrac{1}{3}AC.$

En remplaçant

$AC$ par sa valeur, on trouve :

$AN=\dfrac{1}{3}\times 6=\dfrac{6}{3}=2$

D'où,

$\boxed{AN=2\;cm}$

4) Soient

$O\$ et

$\ P$ les symétriques respectifs des points

$M\$ et

$\ N$ , par rapport à

$A.$

Montrons que

$(MN)$ est parallèle à

$(OP).$

En effet, comme

$O$ est le symétrique de

$M$ par rapport à

$A$ alors,

$A$ est milieu de

$[MO].$

Donc,

$AO=AM$ ce qui entraine :

$\dfrac{AO}{AM}=1$

Aussi, on a :

$P$ symétrique de

$N$ par rapport à

$A$ donc,

$A$ est milieu de

$[NP].$

Ainsi,

$AP=AN$ et par suite :

$\dfrac{AP}{AN}=1$

On constate alors que :

$\dfrac{AO}{AM}=\dfrac{AP}{AN}$

Ainsi,

$M\;,\ A\;,\ O$ étant trois points alignés d'une part, et

$N\;,\ A\;,\ P$ trois points alignés d'autre part, dans le même ordre tels que

$\dfrac{AO}{AM}=\dfrac{AP}{AN}$ alors, en appliquant la réciproque du théorème de Thalès, on a :

$(MN)$ parallèle à

$(OP).$

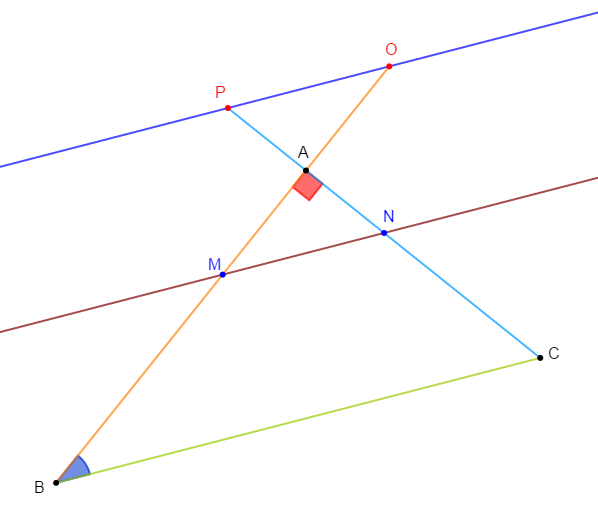
Exercice 20

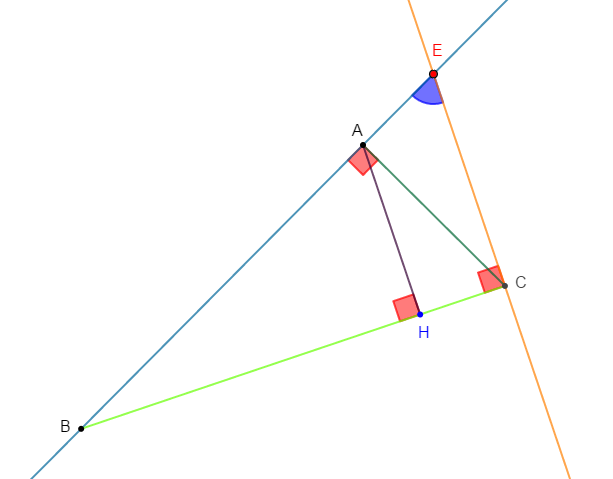
$ABC$ est un triangle rectangle en

$B.$

$H$ est le pied de la hauteur issue de

$B.$

On note

$\alpha$ la mesure de

$\widehat{BCA}.$

On donne :

$\sin(\alpha)=\dfrac{\sqrt{5}}{3}\;;\ BH=\dfrac{\sqrt{5}}{2}\$ et

$\ AC=\sqrt{5}.$

1) a) Sachant que

$\cos^{2}(\alpha)+\sin^{2}(\alpha)=1$ , calculons

$\cos(\alpha).$

On a :

$\begin{array}{rcl} \cos^{2}(\alpha)+\sin^{2}(\alpha)=1&\Rightarrow&\cos^{2}(\alpha)=1-\sin^{2}(\alpha)\\\\&\Rightarrow&\cos(\alpha)=\sqrt{1-\sin^{2}(\alpha)}\\\\&\Rightarrow&\cos(\alpha)=\sqrt{1-\left(\dfrac{\sqrt{5}}{3}\right)^{2}}\\\\&\Rightarrow&\cos(\alpha)=\sqrt{1-\dfrac{5}{9}}\\\\&\Rightarrow&\cos(\alpha)=\sqrt{\dfrac{9}{9}-\dfrac{5}{9}}\\\\&\Rightarrow&\cos(\alpha)=\sqrt{\dfrac{4}{9}}\\\\&\Rightarrow&\cos(\alpha)=\dfrac{\sqrt{4}}{\sqrt{9}}\\\\&\Rightarrow&\cos(\alpha)=\dfrac{2}{3}\end{array}$

Ainsi,

$\boxed{\cos(\alpha)=\dfrac{2}{3}}$

b) Déduisons-en

$HC\$ et

$\ AB.$

Comme

$H$ est le pied de la hauteur issue de

$B$ alors, le triangle

$BHC$ est rectangle en

$H.$

Donc, pour déterminer la longueur

$HC$ , on utilise la tangente de l'angle

$\alpha.$

On a :

$\tan(\alpha)=\dfrac{BH}{HC}$

$\tan(\alpha)=\dfrac{\sin(\alpha)}{\cos(\alpha)}$

Donc,

$\dfrac{BH}{HC}=\dfrac{\sin(\alpha)}{\cos(\alpha)}$

Ce qui entraine :

$HC\times\sin(\alpha)=BH\times\cos(\alpha)$

Ce qui donne :

$HC=\dfrac{BH\times\cos(\alpha)}{\sin(\alpha)}$

Ainsi, en remplaçant

$BH\;,\ \cos(\alpha)\$

$\ \sin(\alpha)$ par leur valeur, on trouve :

$\begin{array}{rcl} HC&=&\dfrac{BH\times\cos(\alpha)}{\sin(\alpha)}\\\\&=&\dfrac{\dfrac{\sqrt{5}}{2}\times\dfrac{2}{3}}{\dfrac{\sqrt{5}}{3}}\\\\&=&\dfrac{\sqrt{5}}{3}\times\dfrac{3}{\sqrt{5}}\\\\&=&\dfrac{3\sqrt{5}}{3\sqrt{5}}\\\\&=&1\end{array}$

D'où,

$\boxed{HC=1\;cm}$

Pour le calcul de

$AB$ , on considère le triangle

$ABC$ rectangle en

$B.$

Alors, on a :

$\sin(\alpha)=\dfrac{AB}{AC}$

Ce qui entraine :

$AB=AC\times\sin(\alpha)$

Donc, en remplaçant

$AC\$ et

$\ \sin(\alpha)$ par leur valeur, on obtient :

$\begin{array}{rcl} AB&=&AC\times\sin(\alpha)\\\\&=&\sqrt{5}\times\dfrac{\sqrt{5}}{3}\\\\&=&\dfrac{\sqrt{5}\times\sqrt{5}}{3}\\\\&=&\dfrac{5}{3}\end{array}$

Ainsi,

$\boxed{AB=\dfrac{5}{3}\;cm}$

2) Une droite

$(\Delta)$ parallèle à

$(BC)$ et passant par

$H$ coupe

$[AB]$ en

$E.$

a) Comparons les mesures des angles

$\widehat{EHA}\$ et

$\ \widehat{BCA}.$

En effet,

$\widehat{EHA}\$ et

$\ \widehat{BCA}$ sont deux angles correspondants.

De plus, les droites

$(\Delta)\$ et

$\ (BC)$ sont parallèles.

Or, on sait que deux droites parallèles coupées par une sécante déterminent deux angles correspondants de même mesure.

Par conséquent,

$mes\,(\widehat{BCA})=mes\,(\widehat{EHA})$

b) Déduisons-en que

$\dfrac{AB}{BC}=\dfrac{EA}{EH}$

Comme les angles

$\widehat{BCA}\$ et

$\ \widehat{EHA}$ ont la même mesure alors, on a :

$\tan\widehat{BCA}=\tan\widehat{EHA}$

Or, dans le triangle rectangle

$ABC$ on a :

$\tan\widehat{BCA}=\dfrac{AB}{BC}$

Par ailleurs, on sait que si deux droites sont perpendiculaires alors, toute droite parallèle à l'une est perpendiculaire à l'autre.

Or,

$(AB)\$ et

$\ (BC)$ sont perpendiculaires et

$(AE)$ parallèle à

$(BC).$

Donc,

$(AE)$ est perpendiculaire à

$(AB)$ en

$E.$

Par conséquent, le triangle

$AEH$ est rectangle en

$E.$

Ainsi, on a :

$\tan\widehat{EHA}=\dfrac{EA}{EH}$

D'où,

$\boxed{\dfrac{AB}{BC}=\dfrac{EA}{EH}}$

Exercice 21

1) Soit un triangle

$ABC$ rectangle en

$A$ tel que

$AB=8\;cm\$ et

$\ AC=4\;cm.$

Calculons

$BC.$

Comme le triangle

$ABC$ est rectangle en

$A$ alors, en appliquant le théorème de Pythagore, on a :

$BC^{2}=AB^{2}+AC^{2}$

Ce qui donne :

$\begin{array}{rcl} BC&=&\sqrt{AB^{2}+AC^{2}}\\\\&=&\sqrt{8^{2}+4^{2}}\\\\&=&\sqrt{64+16}\\\\&=&\sqrt{80}\\\\&=&\sqrt{16\times 5}\\\\&=&4\sqrt{5}\end{array}$

D'où,

$\boxed{BC=4\sqrt{5}}$

2) Soit

$H$ le projeté orthogonal de

$A$ sur

$[BC].$

On donne

$AB^{2}=BH\times BC\$ et

$\ AC^{2}=CH\times BC$

a) Calculons

$BH\;,\ CH$ puis,

$AH.$

Soit :

$AB^{2}=BH\times BC$

Alors, on a :

$BH=\dfrac{AB^{2}}{BC}$

Donc, en remplaçant

$AB\$ et

$\ BC$ par leur valeur, on trouve :

$\begin{array}{rcl} BH&=&\dfrac{AB^{2}}{BC}\\\\&=&\dfrac{8^{2}}{4\sqrt{5}}\\\\&=&\dfrac{64}{4\sqrt{5}}\\\\&=&\dfrac{16}{\sqrt{5}}\\\\&=&\dfrac{16\sqrt{5}}{5}\end{array}$

Ainsi,

$\boxed{BH=\dfrac{16\sqrt{5}}{5}}$

On a :

$AC^{2}=CH\times BC$

Ce qui entraine :

$CH=\dfrac{AC^{2}}{BC}$

Donc, en remplaçant

$AC\$ et

$\ BC$ par leur valeur, on trouve :

$\begin{array}{rcl} CH&=&\dfrac{AC^{2}}{BC}\\\\&=&\dfrac{4^{2}}{4\sqrt{5}}\\\\&=&\dfrac{16}{4\sqrt{5}}\\\\&=&\dfrac{4}{\sqrt{5}}\\\\&=&\dfrac{4\sqrt{5}}{5}\end{array}$

D'où,

$\boxed{CH=\dfrac{4\sqrt{5}}{5}}$

En utilisant la troisième relation métrique, on a :

$AH^{2}=BH\times CH$

Ce qui entraine :

$AH=\sqrt{BH\times CH}$

Donc, en remplaçant

$BH\$ et

$\ CH$ par leur valeur, on obtient :

$\begin{array}{rcl} AH&=&\sqrt{BH\times CH}\\\\&=&\sqrt{\dfrac{16\sqrt{5}}{5}\times\dfrac{4\sqrt{5}}{5}}\\\\&=&\sqrt{\dfrac{16\times 4\times 5}{25}}\\\\&=&\dfrac{4\times 2\times\sqrt{5}}{5}\\\\&=&\dfrac{8\sqrt{5}}{5}\end{array}$

Ainsi,

$\boxed{AH=\dfrac{8\sqrt{5}}{5}}$

b) La parallèle à

$(AH)$ passant par

$C$ coupe

$(AB)$ en

$E.$

Calculons

$AE$ puis déduisons-en

$EC.$

En effet, comme les droites

$(AH)\$ et

$\ (BC)$ sont perpendiculaires et la droite

$(CE)$ parallèle à la droite

$(AH)$ alors,

$(CE)$ est perpendiculaire à

$(BC).$

Par suite, le triangle

$BEC$ est rectangle en

$C.$

Par conséquent,

$[AC]$ est la hauteur issue de

$C.$

Ainsi, en utilisant la troisième relation métrique dans ce triangle, on obtient :

$AC^{2}=AE\times AB$

Ce qui entraine :

$AE=\dfrac{AC^{2}}{AB}$

Donc, en remplaçant

$AC\$ et

$\ AB$ par leur valeur, on trouve :

$\begin{array}{rcl} AE&=&\dfrac{AC^{2}}{AB}\\\\&=&\dfrac{4^{2}}{8}\\\\&=&\dfrac{16}{8}\\\\&=&2\end{array}$

D'où,

$\boxed{AE=2\;cm}$

En utilisant la deuxième relation métrique dans le triangle

$BEC$ , on obtient :

$EC^{2}=AE\times BE$

Ce qui entraine :

$EC=\sqrt{AE\times BE}$

Or,

$BE=AB+AE$ donc,

$EC=\sqrt{AE\times(AB+AE)}$

Ainsi, en remplaçant

$AE\$ et

$\ AB$ par leur valeur, on trouve :

$\begin{array}{rcl} EC&=&\sqrt{AE\times(AB+AE)}\\\\&=&\sqrt{2\times(8+2)}\\\\&=&\sqrt{2\times 10}\\\\&=&\sqrt{20}\\\\&=&\sqrt{4\times 5}\\\\&=&2\sqrt{5}\end{array}$

D'où,

$\boxed{EC=2\sqrt{5}}$

c) Calculons

$\sin\widehat{E}.$

En considérant le triangle

$BEC$ rectangle en

$C$ , on a :

$\sin\widehat{E}=\dfrac{BC}{BE}$

Or,

$BE=AB+AE=8+2=10\;cm$

Donc, en remplaçant

$BC\$ et

$\ BE$ par leur valeur, on trouve :

$\begin{array}{rcl} \sin\widehat{E}&=&\dfrac{BC}{BE}\\\\&=&\dfrac{4\sqrt{5}}{10}\\\\&=&\dfrac{2\sqrt{5}}{5}\end{array}$

D'où,

$\boxed{\sin\widehat{E}=\dfrac{2\sqrt{5}}{5}}$

Exercice 22

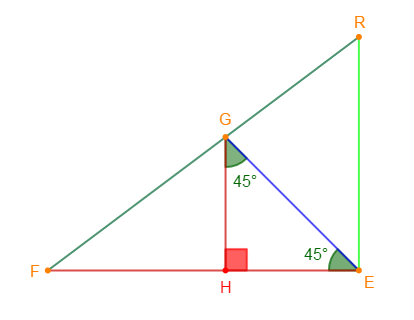
On donne la figure ci-dessous où

$HG=6\;cm$ ,

$\widehat{EGH}=45^{\circ}$ ,

$\sin\widehat{HFG}=\dfrac{3}{5}$ ,

$(GH)$ est la hauteur du triangle

$EFG$ issue de

$G\$ et

$\ (HG)$ parallèle à

$(ER).$

1) Déterminons

$\cos\widehat{HGF}.$

En effet, comme

$(GH)$ est la hauteur du triangle

$EFG$ issue de

$G$ alors, le triangle

$FGH$ est rectangle en

$H.$

Ainsi, les angles aigus

$\widehat{HFG}\$ et

$\ \widehat{HGF}$ sont complémentaires.

Par conséquent, le cosinus de l'un est égal au sinus de l'autre.

Donc,

$\cos\widehat{HGF}=\sin\widehat{HFG}$

D'où,

$\boxed{\cos\widehat{HGF}=\dfrac{3}{5}}$

2) En utilisant les relations trigonométriques dans le triangle rectangle, calculons les longueurs

$FG\$ et

$\ FH.$

$-\$ Calcul

$FG$

Dans le triangle rectangle

$FGH$ , on a :

$\sin\widehat{HFG}=\dfrac{GH}{FG}$

Ce qui entraine :

$FG\times\sin\widehat{HFG}=GH$

Ce qui donne :

$FG=\dfrac{GH}{\sin\widehat{HFG}}$

En remplaçant

$GH\$ et

$\ \sin\widehat{HFG}$ par leur valeur, on trouve :

$\begin{array}{rcl} FG&=&\dfrac{GH}{\sin\widehat{HFG}}\\\\&=&\dfrac{6}{\dfrac{3}{5}}\\\\&=&\dfrac{6\times 5}{3}\\\\&=&\dfrac{30}{3}\\\\&=&10\end{array}$

D'où,

$\boxed{FG=10\;cm}$

$-\$ Calcul

$FH$

Le triangle

$FGH$ étant rectangle en

$H$ alors, d'après le théorème de Pythagore, on a :

$FG^{2}=FH^{2}+HG^{2}$

Donc,

$FH^{2}=FG^{2}-HG^{2}$

Par suite,

$FH=\sqrt{FG^{2}-HG^{2}}$

En remplaçant

$FG\$ et

$\ HG$ par leur valeur, on trouve :

$\begin{array}{rcl} FH&=&\sqrt{FG^{2}-HG^{2}}\\\\&=&\sqrt{10^{2}-6^{2}}\\\\&=&\sqrt{100-36}\\\\&=&\sqrt{64}\\\\&=&8\end{array}$

D'où,

$\boxed{FH=8\;cm}$

3) Justifions que le triangle

$EGH$ est rectangle et isocèle en

$H$ puis, déduisons-en

$EH.$

En effet,

$(GH)$ étant perpendiculaire à

$(HE)$ alors, le triangle

$EGH$ est rectangle en

$H.$

Par ailleurs, on sait que la somme des angles d'un triangle est égale à

$180^{\circ}.$

Donc,

$\widehat{EGH}+\widehat{GEH}+\widehat{GHE}=180^{\circ}$

Par suite,

$\widehat{GEH}=180^{\circ}-\widehat{EGH}-\widehat{GHE}$

En remplaçant

$\widehat{EGH}\$ et

$\ \widehat{GHE}$ par leur valeur, on trouve :

$\begin{array}{rcl} \widehat{GEH}&=&180^{\circ}-\widehat{EGH}-\widehat{GHE}\\\\&=&180^{\circ}-45^{\circ}-90^{\circ}\\\\&=&45^{\circ}\end{array}$

Ainsi,

$\boxed{\widehat{GEH}=45^{\circ}}$

On remarque alors que les angles

$\widehat{GEH}\$ et

$\ \widehat{EGH}$ ont la même mesure.

Par conséquent, le triangle

$EGH$ est rectangle et isocèle en

$H.$

4) Calculons la longueur

$RE.$

$(HG)$ étant parallèle à

$(ER)$ alors, les triangles

$FGH\$ et

$\ FRE$ sont en position de Thalès.

Donc, en appliquant le théorème de Thalès, on a :

$\dfrac{GH}{RE}=\dfrac{FH}{FE}$

Ce qui entraine :

$RE\times FH=GH\times FE$

Ainsi,

$RE=\dfrac{GH\times FE}{FH}$

Or,

$FE=FH+HE=8+6=14\;cm$

Donc, en remplaçant

$GH\;,\ FH\$ et

$\ FE$ par leur valeur, on trouve :

$\begin{array}{rcl} RE&=&\dfrac{GH\times FE}{FH}\\\\&=&\dfrac{6\times 14}{8}\\\\&=&\dfrac{84}{8}\\\\&=&\dfrac{21}{4}\end{array}$

D'où,

$\boxed{RE=\dfrac{21}{4}}$

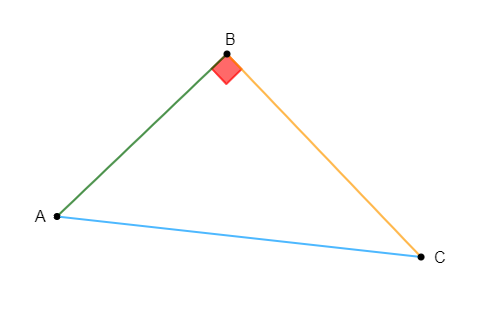
Exercice de Synthèse

Soit

$ABC$ un triangle rectangle en

$B$ et

$AC$ l'hypoténuse,

$\sin\widehat{A}$ est égal :

$\dfrac{BC}{AC}$

Auteur:

Diny Faye

Commentaires

Anonyme (non vérifié)

mar, 05/14/2019 - 03:31

Permalien

Je suis fière de vous

répondre

Anonyme (non vérifié)

mar, 01/14/2020 - 00:18

Permalien

Je veux la correction de l

Je veux la correction de l'exercice 11

répondre

Anonyme (non vérifié)

dim, 01/19/2020 - 03:08

Permalien

Je veux la correction de l

Je veux la correction de l'exercice 19

répondre

Anonyme (non vérifié)

sam, 02/13/2021 - 22:25

Permalien

Je veux la correction de l

Je veux la correction de l exercice 19

répondre

Younousstall (non vérifié)

mer, 02/24/2021 - 21:59

Permalien

Je veux la correction des

Je veux la correction des exercices 23, 24, 25,26

répondre

Lika (non vérifié)

mer, 02/05/2020 - 21:56

Permalien

Demande

Je veux la correction de l'exercice 26

répondre

Anonyme (non vérifié)

ven, 03/20/2020 - 14:01

Permalien

Je veux la correction de l

Je veux la correction de l'exercice 17

répondre

Malick lo (non vérifié)

mar, 03/22/2022 - 16:32

Permalien

https://t.me/+NoOyIVdXEygyZWVk

répondre

Anonyme (non vérifié)

mer, 01/27/2021 - 20:51

Permalien

Appris

répondre

Anonyme (non vérifié)

mer, 01/27/2021 - 20:51

Permalien

Yes

répondre

Anonyme (non vérifié)

mer, 01/27/2021 - 20:52

Permalien

Yes

répondre

Anonyme (non vérifié)

jeu, 02/11/2021 - 23:09

Permalien

merci beaucoup

répondre

Amy Diouf. (non vérifié)

mar, 02/16/2021 - 15:21

Permalien

Je veux la correction de l

Je veux la correction de l'exercice 12 en 3 ém de math sur les exercices de trigonométrie

répondre

Younousstall (non vérifié)

mer, 02/24/2021 - 21:55

Permalien

Je veux la correction des

Je veux la correction des exercices 23,24,25,26

répondre

Anonyme (non vérifié)

sam, 02/27/2021 - 11:25

Permalien

Correction exercice 23

répondre

Anonyme (non vérifié)

sam, 02/27/2021 - 16:03

Permalien

Je veux la correction de l

Je veux la correction de l'exercice 13 et 14 svp je suis coincée

répondre

Anonyme (non vérifié)

dim, 02/28/2021 - 00:02

Permalien

Est-ce qu'on peut avoir la

Est-ce qu'on peut avoir la correction des exos

répondre

Anonyme (non vérifié)

ven, 03/12/2021 - 10:09

Permalien

J veux la correction exo16

J veux la correction exo16 svp

répondre

Diané (non vérifié)

dim, 03/21/2021 - 17:43

Permalien

Je veux la correction de 15

répondre

Diané (non vérifié)

dim, 03/21/2021 - 17:43

Permalien

Je veux la correction de 15

répondre

Amadou faye (non vérifié)

dim, 03/21/2021 - 21:12

Permalien

je voudrais avoir la correction de l'exercice 15 svp

je voudrais avoir la correction de l'exercice 15

répondre

Amadou faye (non vérifié)

dim, 03/21/2021 - 21:12

Permalien

je voudrais avoir la correction de l'exercice 15 svp

je voudrais avoir la correction de l'exercice 15

répondre

Marame tall (non vérifié)

jeu, 04/08/2021 - 09:05

Permalien

Je veux la correction de

Je veux la correction de exercice16

répondre

Marame tall (non vérifié)

jeu, 04/08/2021 - 09:03

Permalien

Je la correction de l

Je la correction de l'exercice 16

répondre

Anonyme (non vérifié)

lun, 07/05/2021 - 16:03

Permalien

Intéressant

répondre

Anonyme (non vérifié)

lun, 07/05/2021 - 16:03

Permalien

Intéressant

répondre

Anonyme (non vérifié)

ven, 08/27/2021 - 03:38

Permalien

Correction de l'exo 14 svp

répondre

Mariama (non vérifié)

jeu, 01/05/2023 - 07:43

Permalien

Exercice 14

Correction

répondre

Moustapha Ndoye (non vérifié)

lun, 07/18/2022 - 14:32

Permalien

Je veux la correction d

Je veux la correction d'exercice 5

répondre

Moustapha Ndoye (non vérifié)

lun, 07/18/2022 - 14:33

Permalien

Je veux la correction d

Je veux la correction d'exercice 5

répondre

maman Niang (non vérifié)

mer, 12/14/2022 - 19:27

Permalien

la correction 12 et 17

répondre

Anonyme (non vérifié)

dim, 01/07/2024 - 18:09

Permalien

machallah merci beaucoup

machallah merci beaucoup sunudaara

répondre

Anonyme (non vérifié)

dim, 01/07/2024 - 18:09

Permalien

machallah merci beaucoup

machallah merci beaucoup sunudaara

répondre

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.

Vous êtes ici

Solution des exercices : Trigonométrie 3e

Formulaire de recherche

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Exercice 5

Exercice 6

Exercice 7

Exercice 8

Exercice 9

Exercice 10

Exercice 11

Exercice 12

Exercice 13

Exercice 14

Exercice 15

Exercice 16

Exercice 17

Exercice 18

Exercice 19

Exercice 20

Exercice 21

Exercice 22

Exercice de Synthèse

Commentaires

Ajouter un commentaire

Plain text