Solution des exercices : repérage 3e
Classe:
Troisième
Exercice 1
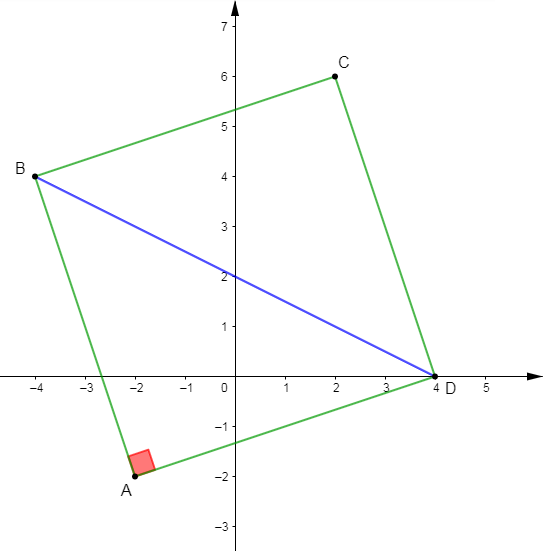
On donne : $A(-2\;;\ -2)\;;\ B(-4\;;\ 4)\;;\ C(2\;;\ 6)\ $ et $\ D(4\;;\ 0).$
1) Vérifions si $\overrightarrow{AB}\ $ et $\ \overrightarrow{AD}$ sont orthogonaux.
En calculant les coordonnées de ces deux vecteurs, on obtient :
$\overrightarrow{AB}\begin{pmatrix} -4-(-2)\\4-(-2)\end{pmatrix}=\begin{pmatrix} -2\\6\end{pmatrix}$
$\overrightarrow{AD}\begin{pmatrix} 4-(-2)\\0-(-2)\end{pmatrix}=\begin{pmatrix} 6\\2\end{pmatrix}$
Ainsi, on a :
$\begin{array}{rcl} (x_{_{\overrightarrow{AB}}}\times x_{_{\overrightarrow{AD}}})+(y_{_{\overrightarrow{AB}}}\times y_{_{\overrightarrow{AD}}})&=&(-2\times 6)+(6\times 2)\\\\&=&-12+12\\\\&=&0\end{array}$
Donc, $\boxed{(x_{_{\overrightarrow{AB}}}\times x_{_{\overrightarrow{AD}}})+(y_{_{\overrightarrow{AB}}}\times y_{_{\overrightarrow{AD}}})=0}$
Ce qui signifie que les coordonnées des vecteurs $\overrightarrow{AB}\ $ et $\ \overrightarrow{AD}$ vérifient la condition d'orthogonalité.
Par conséquent, $\overrightarrow{AB}\ $ et $\ \overrightarrow{AD}$ sont orthogonaux.
2) Calculons les distances $AB\ $ et $\ AD.$
Soit : $\overrightarrow{AB}\begin{pmatrix} -2\\6\end{pmatrix}$ alors, on a :
$\begin{array}{rcl} AB&=&\sqrt{(-2)^{2}+(6)^{2}}\\\\&=&\sqrt{4+36}\\\\&=&\sqrt{40}\\\\&=&2\sqrt{10}\end{array}$
Donc, $\boxed{AB=2\sqrt{10}}Ê$
Soit : $\overrightarrow{AD}\begin{pmatrix} 6\\2\end{pmatrix}$ alors, on a :
$\begin{array}{rcl} AD&=&\sqrt{(6)^{2}+(2)^{2}}\\\\&=&\sqrt{36+4}\\\\&=&\sqrt{40}\\\\&=&2\sqrt{10}\end{array}$
D'où, $\boxed{AD=2\sqrt{10}}$
3) Déterminons la nature du triangle $ABD.$
En effet, on sait que les vecteurs $\overrightarrow{AB}\ $ et $\ \overrightarrow{AD}$ sont orthogonaux.
De plus, d'après le résultat de la question $2)$, on remarque que $AB=AD.$
Par conséquent, le triangle $ABD$ est rectangle isocèle en $A.$
4) Démontrons que le quadrilatère $ABCD$ est un carré.
Pour cela, vérifions d'abord que c'est parallélogramme.
En effet, en calculant les coordonnées du vecteur $\overrightarrow{DC}$, on trouve :
$\overrightarrow{DC}\begin{pmatrix} 2-4\\6-0\end{pmatrix}=\begin{pmatrix} -2\\6\end{pmatrix}$
Alors, on constate que les vecteurs $\overrightarrow{AB}\ $ et $\ \overrightarrow{AD}$ ont les mêmes coordonnées.
Ainsi, $\overrightarrow{AB}=\overrightarrow{DC}$
D'où, $ABCD$ est un parallélogramme.
Par ailleurs, on a : $\overrightarrow{AB}\perp\overrightarrow{AD}\ $ et $\ AB=AD.$
Donc, le quadrilatère $ABCD$ est un parallélogramme dont deux côtés perpendiculaires ont même longueur.
Par conséquent, c'est un carré.
Exercice 2
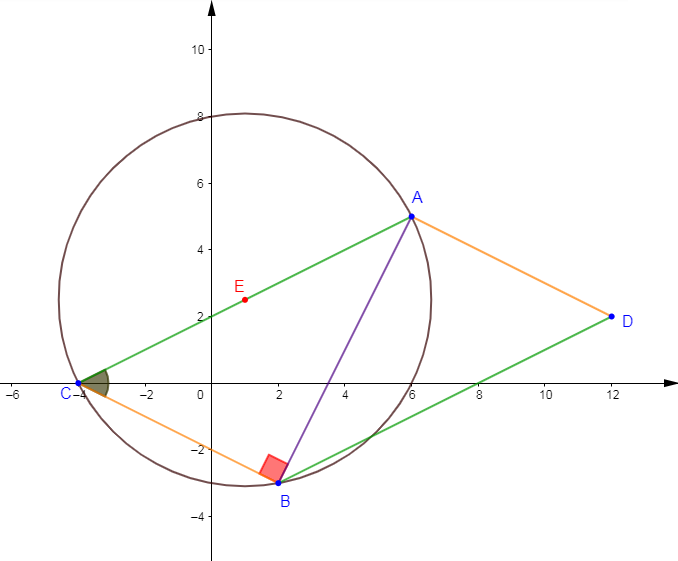
Le plan est muni d'un repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j}).$ On considère les points $A(6\;,\ 5)\;;\ B(2\;,\ -3)\ $ et $\ C(-4\;,\ 0).$
1) Faisons la figure en utilisant le centimètre comme unité.
2) Calculons les distances $AB\;,\ AC\ $ et $\ BC.$
Soit : $\overrightarrow{AB}\begin{pmatrix} 2-6\\-3-5\end{pmatrix}=\begin{pmatrix} -4\\-8\end{pmatrix}$ alors, on a :
$\begin{array}{rcl} AB&=&\sqrt{(-4)^{2}+(-8)^{2}}\\\\&=&\sqrt{16+64}\\\\&=&\sqrt{80}\\\\&=&\sqrt{16\times 5}\\\\&=&\sqrt{16}\times\sqrt{5}\\\\&=&4\sqrt{5}\end{array}$
Donc, $\boxed{AB=4\sqrt{5}}$
Soit : $\overrightarrow{AC}\begin{pmatrix} -4-6\\0-5\end{pmatrix}=\begin{pmatrix} -10\\-5\end{pmatrix}$ alors, on a :
$\begin{array}{rcl} AC&=&\sqrt{(-10)^{2}+(-5)^{2}}\\\\&=&\sqrt{100+25}\\\\&=&\sqrt{125}\\\\&=&\sqrt{25\times 5}\\\\&=&\sqrt{25}\times\sqrt{5}\\\\&=&5\sqrt{5}\end{array}$
D'où, $\boxed{AC=5\sqrt{5}}$
Soit : $\overrightarrow{BC}\begin{pmatrix} -4-2\\0-(-3)\end{pmatrix}=\begin{pmatrix} -6\\3\end{pmatrix}$ alors, on a :
$\begin{array}{rcl} BC&=&\sqrt{(-6)^{2}+(3)^{2}}\\\\&=&\sqrt{36+9}\\\\&=&\sqrt{45}\\\\&=&\sqrt{9\times 5}\\\\&=&\sqrt{9}\times\sqrt{5}\\\\&=&3\sqrt{5}\end{array}$
Ainsi, $\boxed{BC=3\sqrt{5}}$
3) Déduisons la nature du triangle $ABC.$
D'après le résultat de question $2)$, on a :
$AB^{2}=(4\sqrt{5})^{2}=80$
$AC^{2}=(5\sqrt{5})^{2}=125$
$BC^{2}=(3\sqrt{5})^{2}=45$
Alors, on remarque que : $80+45=125$
Ce qui signifie que : $AB^{2}+BC^{2}=AC^{2}.$
Ainsi, d'après la réciproque du théorème de Pythagore $ABC$ est un triangle rectangle en $B.$
4) Calculons l'aire du triangle $ABC$
Soit : $\mathcal{A}$ l'aire du triangle $ABC.$
Comme le triangle est rectangle en $B$ alors, on a :
$\begin{array}{rcl}\mathcal{A}&=&\dfrac{AB\times BC}{2}\\\\&=&\dfrac{4\sqrt{5}\times 3\sqrt{5}}{2}\\\\&=&\dfrac{12\times 5}{2}\\\\&=&30\end{array}$
D'où, $\boxed{\mathcal{A}=30\;cm^{2}}$
5) Calculons le périmètre du triangle $ABC$,
Soit : $p$ le périmètre du triangle $ABC.$
Alors, on a :
$\begin{array}{rcl} p&=&AB+BC+AC\\\\&=&4\sqrt{5}+3\sqrt{5}+5\sqrt{5}\\\\&=&12\sqrt{5}\end{array}$
Ainsi, $\boxed{p=12\sqrt{5}=26.8\;cm}$
6) On considère le cercle circonscrit au triangle $ABC.$
a) Comme $ABC$ est un triangle rectangle en $B$, alors le cercle circonscrit à ce triangle a pour centre le milieu de l'hypoténuse, $[AC].$
Donc si $E$ est le centre de ce cercle, alors $E$ a pour coordonnées $$\begin{pmatrix} \dfrac{6+(-4)}{2}\\ \\ \dfrac{5+0}{2}\end{pmatrix}=\begin{pmatrix} 1\\ \\ \dfrac{5}{2}\end{pmatrix}$$
b) Déterminons la valeur exacte du rayon de ce cercle.
Soit $r$ le rayon de ce cercle.
Comme $[AC]$ est un diamètre alors, le rayon $r$ est donné par : $r=\dfrac{AC}{2}$
D'où, $\boxed{r=\dfrac{5\sqrt{5}}{2}}$
7) Calculons la valeur de $\tan\widehat{ACB}$ puis une valeur approchée de l'angle $\widehat{ACB}.$
Comme le triangle $ABC$ est rectangle en $B$ alors, $\tan\widehat{ACB}$ est donnée par :
$$\tan\widehat{ACB}=\dfrac{\text{côté opposé à l'angle }\widehat{ACB}}{\text{côté adjacent à l'angle }\widehat{ACB}}$$
Donc, on a :
$\begin{array}{rcl}\tan\widehat{ACB}&=&\dfrac{AB}{BC}\\\\&=&\dfrac{4\sqrt{5}}{3\sqrt{5}}\\\\&=&\dfrac{4}{3} \end{array}$
D'où, $\boxed{\tan\widehat{ACB}=\dfrac{4}{3}}$
Ainsi, une valeur approchée de l'angle $\widehat{ACB}$ est égale à $53^{\circ}.$
8) Calculons les coordonnées du vecteur $\overrightarrow{CA}.$
On a : $\overrightarrow{CA}\begin{pmatrix} 6-(-4)\\5-0\end{pmatrix}=\begin{pmatrix} 10\\5\end{pmatrix}$
En déduisons les coordonnées du point $D$ pour que $ACBD$ soit un parallélogramme.
En effet, $ACBD$ étant un parallélogramme, alors, $\overrightarrow{CA}=\overrightarrow{BD}$
Donc, les vecteurs $\overrightarrow{CA}\ $ et $\ \overrightarrow{BD}$ ont mêmes coordonnées.
Ce qui signifie : $\begin{pmatrix} 10\\5\end{pmatrix}=\begin{pmatrix} x_{D}-2\\y_{D}-(-3)\end{pmatrix}$
Ainsi, $\left\lbrace\begin{array}{rcl}x_{D}-2&=&10\\\\y_{D}+3&=&5\end{array}\right.\ \Leftrightarrow\ \left\lbrace\begin{array}{rcccl} x_{D}&=&10+2&=&12\\\\y_{D}&=&5-3&=&2\end{array}\right.$
D'où, $$\boxed{D\begin{pmatrix} 12\\2\end{pmatrix}}$$
Exercice 3
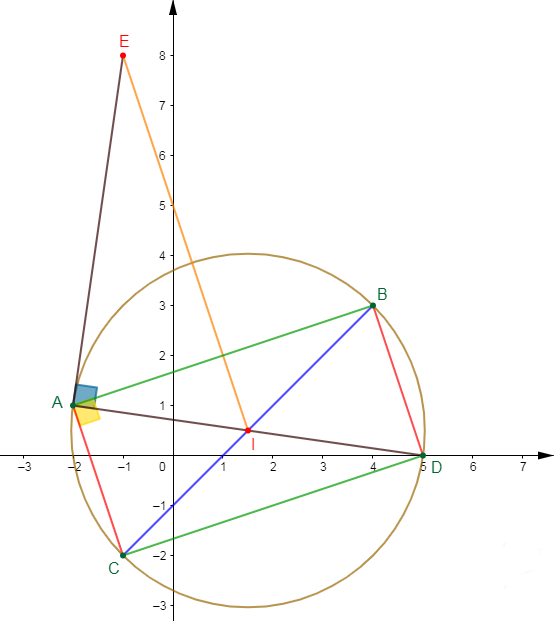
On donne les points : $A(-2;\ 1)\;;\ B(4;\ 3)\;;\ C(-1;\ y)\quad (y\in\mathbb{R})$

1) Calculons $y$ pour que les vecteurs $\overrightarrow{AB}\ $ et $\ \overrightarrow{AC}$ soient orthogonaux.
Déterminons d'abord les coordonnées des vecteurs $\overrightarrow{AB}\ $ et $\ \overrightarrow{AC}.$
On a :
$\overrightarrow{AB}\begin{pmatrix} 4-(-2)\\3-1\end{pmatrix}=\begin{pmatrix} 6\\2\end{pmatrix}$
$\overrightarrow{AC}\begin{pmatrix} -1-(-2)\\y-1\end{pmatrix}=\begin{pmatrix} 1\\y-1\end{pmatrix}$
Alors, on sait que : $\overrightarrow{AB}\ $ et $\ \overrightarrow{AC}$ sont orthogonaux si, et seulement si, leurs coordonnées vérifient la condition d'orthogonalité.
C'est-à-dire ;
$$(x_{_{\overrightarrow{AB}}}\times x_{_{\overrightarrow{AC}}})+(y_{_{\overrightarrow{AB}}}\times y_{_{\overrightarrow{AC}}})=0$$
Donc, on a :
$\begin{array}{rcl}\overrightarrow{AB}\perp \overrightarrow{AC}&\Leftrightarrow&(x_{_{\overrightarrow{AB}}}\times x_{_{\overrightarrow{AC}}})+(y_{_{\overrightarrow{AB}}}\times y_{_{\overrightarrow{AC}}})=0\\\\&\Leftrightarrow&(6\times 1)+(2\times(y-1))=0\\\\&\Leftrightarrow&6+2y-2=0\\\\&\Leftrightarrow&2y+4=0\\\\&\Leftrightarrow&2y=-4\\\\&\Leftrightarrow&y=\dfrac{-4}{2}\\\\&\Leftrightarrow&y=-2\end{array}$
Ainsi, $$\boxed{C\begin{pmatrix} -1\\-2\end{pmatrix}}$$
2) a) Soit $I$ le milieu de $[BC]$ ; calculons les cordonnées de $I.$
Les coordonnées de $I$ sont données par :
$$x_{I}=\dfrac{x_{B}+x_{C}}{2}\quad \text{et}\quad y_{I}=\dfrac{y_{B}+y_{C}}{2}$$
Soit alors : $x_{I}=\dfrac{4-1}{2}=\dfrac{3}{2}\quad$ et $\quad y_{I}=\dfrac{3-2}{2}=\dfrac{1}{2}$
Donc, $$\boxed{I\begin{pmatrix} \dfrac{3}{2}\\ \\ \dfrac{1}{2}\end{pmatrix}}$$
b) Soit $D$ le symétrique de $A$ par rapport à $I$. Calculons les coordonnées de $D.$
En effet, comme $D$ est le symétrique de $A$ par rapport à $I$ alors, $I$ est milieu de $[AD]$ et on a :
$$\overrightarrow{ID}=\overrightarrow{AI}$$
Alors, en calculant les coordonnées de $\overrightarrow{AI}\ $ et $\ \overrightarrow{ID}$, on obtient :
$\overrightarrow{AI}\begin{pmatrix} \dfrac{3}{2}-(-2)\\ \\ \dfrac{1}{2}-1\end{pmatrix}=\begin{pmatrix} \dfrac{3}{2}+2\\ \\ \dfrac{1}{2}-1\end{pmatrix}$
$\overrightarrow{ID}\begin{pmatrix} x_{D}-\dfrac{3}{2}\\ \\ y_{D}-\dfrac{1}{2}\end{pmatrix}$
Ainsi, on a :
$\begin{array}{rcl}\overrightarrow{ID}=\overrightarrow{AI}&\Leftrightarrow&\left\lbrace\begin{array}{rcl}x_{D}-\dfrac{3}{2}&=&\dfrac{3}{2}+2\\\\ y_{D}-\dfrac{1}{2}&=&\dfrac{1}{2}-1\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl}x_{D}&=&\dfrac{3}{2}+\dfrac{3}{2}+2\\\\ y_{D}&=&\dfrac{1}{2}+\dfrac{1}{2}-1\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl}x_{D}&=&5\\\\ y_{D}&=&0\end{array}\right.\end{array}$
D'où, $$\boxed{D\begin{pmatrix} 5\\ 0\end{pmatrix}}$$
3) Soit $\vec{u}\begin{pmatrix} 1\\ 7\end{pmatrix}.$ Calculons les coordonnées du point $E$, image de $A$ par la translation de vecteur $\vec{u}$
En effet, $E$ est image de $A$ par la translation de vecteur $\vec{u}$ donc, on a :
$$\overrightarrow{AE}=\vec{u}$$
Soit alors :
$\overrightarrow{AE}\begin{pmatrix} x_{E}-(-2)\\ y_{E}-1\end{pmatrix}=\begin{pmatrix} x_{E}+2\\ y_{E}-1\end{pmatrix}$
$\vec{u}\begin{pmatrix} 1\\ 7\end{pmatrix}$
Ainsi, on a :
$\begin{array}{rcl}\overrightarrow{AE}=\vec{u}&\Leftrightarrow&\left\lbrace\begin{array}{rcl}x_{E}+2&=&1\\\\ y_{E}-1&=&7\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl}x_{E}&=&1-2\\\\ y_{E}&=&7+1\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl}x_{E}&=&-1\\\\ y_{E}&=&8\end{array}\right.\end{array}$
D'où, $$\boxed{E\begin{pmatrix} -1\\ 8\end{pmatrix}}$$
4) Démontrons que $ABDC$ est un rectangle.
Vérifions d'abord que $ABDC$ est un parallélogramme.
Pour cela, calculons les coordonnées du vecteur $\overrightarrow{CD}.$
On a : $\overrightarrow{CD}\begin{pmatrix} 5-(-1)\\0-(-2)\end{pmatrix}=\begin{pmatrix} 6\\2\end{pmatrix}$
On constate alors que les vecteurs $\overrightarrow{AB}\ $ et $\ \overrightarrow{CD}$ ont les mêmes coordonnées.
Ainsi, $\overrightarrow{AB}=\overrightarrow{CD}$
Par conséquent, $ABDC$ est un parallélogramme.
Par ailleurs, d'après le résultat de la question $1)$, on a : $\overrightarrow{AB}\ $ et $\ \overrightarrow{AC}$ sont orthogonaux.
Donc, pour que $ABDC$ soit un rectangle, il suffit que $AB\neq AC$
Calculons alors les longueurs $AB\ $ et $\ AC.$
Soit : $\overrightarrow{AB}\begin{pmatrix} 6\\2\end{pmatrix}\ $ et $\ \overrightarrow{AC}\begin{pmatrix} 1\\-3\end{pmatrix}$
On a :
$\begin{array}{rcl} AB&=&\sqrt{(6)^{2}+(2)^{2}}\\\\&=&\sqrt{36+4}\\\\&=&\sqrt{40}\\\\&=&2\sqrt{10}\end{array}$
Donc, $\boxed{AB=2\sqrt{10}}$
$\begin{array}{rcl} AC&=&\sqrt{(1)^{2}+(-3)^{2}}\\\\&=&\sqrt{1+9}\\\\&=&\sqrt{10}\end{array}$
Donc, $\boxed{AC=\sqrt{10}}$
Alors, on constate que les longueurs $AB\ $ et $\ AC$ sont différentes.
Ainsi, $ABDC$ est un parallélogramme dont deux côtés consécutifs orthogonaux sont de longueurs différentes.
Par conséquent, c'est un rectangle.
Montrons que les points $A\;,\ B\;,\ C\ $ et $\ D$ appartiennent à un même cercle.
En effet, comme $ABDC$ est un rectangle alors, ses angles opposés sont supplémentaires.
Par conséquent, le quadrilatère $ABDC$ est inscriptible dans un cercle.
Ce qui signifie que les sommets $A\;,\ B\;,\ C\ $ et $\ D$ appartiennent à un même cercle.
C'est le cercle dont le centre est le point $I$ ; centre de ce rectangle.
5) Démontrons que $AEI$ est un triangle rectangle.
Pour cela, vérifions que $\overrightarrow{AE}\ $ et $\ \overrightarrow{AI}$ sont orthogonaux.
Calculons alors les coordonnées de ces deux vecteurs.
On trouve alors :
$\overrightarrow{AE}\begin{pmatrix} -1-(-2)\\8-1\end{pmatrix}=\begin{pmatrix} 1\\7\end{pmatrix}$
$\overrightarrow{AI}\begin{pmatrix} \dfrac{3}{2}-(-2)\\ \\ \dfrac{1}{2}-1\end{pmatrix}=\begin{pmatrix} \dfrac{7}{2}\\ \\ -\dfrac{1}{2}\end{pmatrix}$
Ainsi, on a :
$\begin{array}{rcl} (x_{_{\overrightarrow{AE}}}\times x_{_{\overrightarrow{AI}}})+(y_{_{\overrightarrow{AE}}}\times y_{_{\overrightarrow{AI}}})&=&\left(1\times\dfrac{7}{2}\right)+\left(7\times\left(-\dfrac{1}{2}\right)\right)\\\\&=&\dfrac{7}{2}-\dfrac{7}{2}\\\\&=&0\end{array}$
Donc, $\boxed{(x_{_{\overrightarrow{AE}}}\times x_{_{\overrightarrow{AI}}})+(y_{_{\overrightarrow{AE}}}\times y_{_{\overrightarrow{AI}}})=0}$
Ce qui signifie que les coordonnées des vecteurs $\overrightarrow{AE}\ $ et $\ \overrightarrow{AI}$ vérifient la condition d'orthogonalité.
Par conséquent, $\overrightarrow{AE}\ $ et $\ \overrightarrow{AI}$ sont orthogonaux.
D'où, $AEI$ est un triangle rectangle en $A.$
6) Établissons une équation réduite de la droite $(AE).$
Soit : $y=ax+b$ une équation réduite de la droite $(AE)$
Déterminons alors $a\ $ et $\ b$
En effet, d'après le résultat de la question $3)$, on a : $\overrightarrow{AE}=\vec{u}.$
Ce qui signifie que $\vec{u}$ est un vecteur directeur de la droite $(AE).$
Donc, le coefficient $a$ est donné par :
$$a=\dfrac{7}{1}=7$$
Par suite, $y=7x+b$
Par ailleurs, on sait que : la droite $(AE)$ passe par le point $A.$
Donc, les coordonnées de $A$ vérifient l'équation de $(AE).$
C'est-à-dire ; $y_{A}=7\times x_{A}+b$
Soit alors ; $1=7\times(-2)+b$
Ce qui donne : $1=-14+b$
D'où,
$$b=15$$
Ainsi, une équation réduite de la droite $(AE)$ est :
$$\boxed{y=7x+15}$$
Exercice 4
Un plan $P$ est rapporté à un repère orthonormé $(O\;;\ \vec{i}\;,\ \vec{j}).$
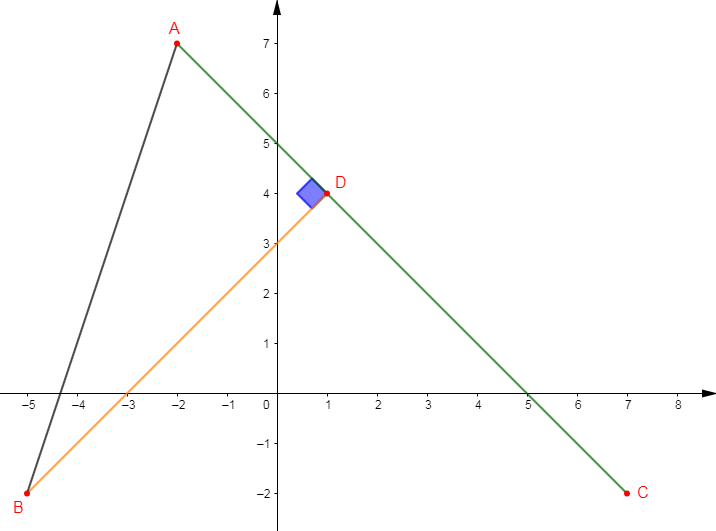
1) Plaçons les points $A\;,\ B\ $ et $\ C$ donnés par les coordonnées :
$$A(-1.5\;;\ 2)\;;\ B(1.5\;;\ -2)\;;\ C(6.5\;;\ 8)$$
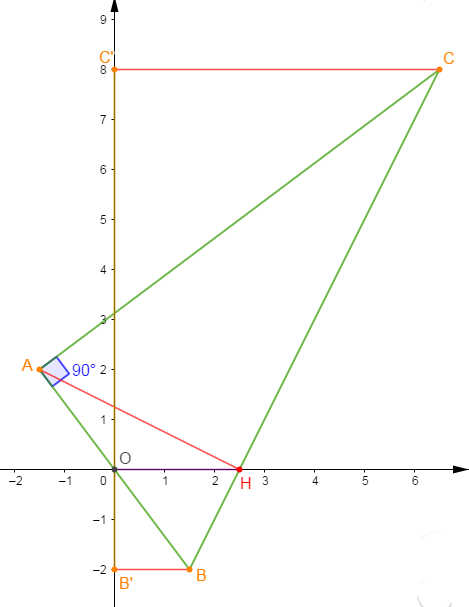
Montrons que $O\begin{pmatrix} 0\\0\end{pmatrix}$ est le milieu de $[AB]$
$O$ est milieu de $[AB]$ si, et seulement si, ses coordonnées vérifient :
$$x_{O}=\dfrac{x_{A}+x_{B}}{2}\quad\text{et}\quad y_{O}=\dfrac{y_{A}+y_{B}}{2}$$
Calculons alors : $\dfrac{x_{A}+x_{B}}{2}\ $ et $\ \dfrac{y_{A}+y_{B}}{2}$
On a :
$\begin{array}{rcl}\dfrac{x_{A}+x_{B}}{2}&=&\dfrac{-1.5+1.5}{2}\\\\&=&\dfrac{0}{2}\\\\&=&0 \end{array}$
Donc, $\boxed{\dfrac{x_{A}+x_{B}}{2}=0}$
$\begin{array}{rcl}\dfrac{y_{A}+y_{B}}{2}&=&\dfrac{2-2}{2}\\\\&=&\dfrac{0}{2}\\\\&=&0 \end{array}$
Alors, $\boxed{\dfrac{y_{A}+y_{B}}{2}=0}$
Par suite,
$$\left\lbrace\begin{array}{rcl} x_{O}&=&\dfrac{x_{A}+x_{B}}{2}\\\\y_{O}&=&\dfrac{y_{A}+y_{B}}{2}\end{array}\right.$$
D'où, $O$ est le milieu du segment $[AB]$
2) Calculons les distances $AB\;;\ AC\ $ et $\ BC$
Soit : $\overrightarrow{AB}\begin{pmatrix} 1.5-(-1.5)\\-2-2\end{pmatrix}=\begin{pmatrix} 3\\-4\end{pmatrix}$ alors, on a :
$\begin{array}{rcl} AB&=&\sqrt{(3)^{2}+(-4)^{2}}\\\\&=&\sqrt{9+16}\\\\&=&\sqrt{25}\\\\&=&5\end{array}$
Donc, $\boxed{AB=5\;cm}$
Soit : $\overrightarrow{AC}\begin{pmatrix} 6.5-(-1.5)\\8-2\end{pmatrix}=\begin{pmatrix} 8\\6\end{pmatrix}$ alors, on a :
$\begin{array}{rcl} AC&=&\sqrt{(8)^{2}+(6)^{2}}\\\\&=&\sqrt{64+36}\\\\&=&\sqrt{100}\\\\&=&10\end{array}$
Ainsi, $\boxed{AC=10\;cm}$
Soit : $\overrightarrow{BC}\begin{pmatrix} 6.5-1.5\\8-(-2)\end{pmatrix}=\begin{pmatrix} 5\\10\end{pmatrix}$ alors, on a :
$\begin{array}{rcl} BC&=&\sqrt{(5)^{2}+(10)^{2}}\\\\&=&\sqrt{25+100}\\\\&=&\sqrt{125}\\\\&=&\sqrt{25\times 5}\\\\&=&\sqrt{25}\times\sqrt{5}\\\\&=&5\sqrt{5}\end{array}$
Donc, $\boxed{BC=5\sqrt{5}\;cm}$
Montrons que le triangle $ABC$ est rectangle.
D'après ce qui précède, on a :
$AB^{2}=(5)^{2}=25$
$AC^{2}=(10)^{2}=100$
$BC^{2}=(5\sqrt{5})^{2}=125$
Alors, on constate que : $25+100=125$
Ce qui signifie que : $AB^{2}+AC^{2}=BC^{2}.$
Ainsi, d'après la réciproque du théorème de Pythagore $ABC$ est un triangle rectangle en $A.$
3) Soit $H$ le projeté orthogonal de $A$ sur la droite $(BC).$
Calculons $BH\;,\ CH\ $ et $\ AH$
$-\ $ Calcul de $BH$
D'après la première relation métrique, on a :
$$AB^{2}=BH\times BC$$
Donc,
$\begin{array}{rcl} BH&=&\dfrac{AB^{2}}{BC}\\\\&=&\dfrac{5^{2}}{5\sqrt{5}}\\\\&=&\dfrac{5}{\sqrt{5}}\\\\&=&\dfrac{5\times\sqrt{5}}{(\sqrt{5})\times(\sqrt{5})}\\\\&=&\dfrac{5\sqrt{5}}{5}\\\\&=&\sqrt{5}\end{array}$
D'où, $\boxed{BH=\sqrt{5}\;cm}$
$-\ $ Calcul de $CH$
D'après la deuxième relation métrique, on a :
$$AC^{2}=CH\times BC$$
Par suite,
$\begin{array}{rcl} CH&=&\dfrac{AC^{2}}{BC}\\ \\&=&\dfrac{10^{2}}{5\sqrt{5}}\\ \\&=&\dfrac{100}{5\sqrt{5}}\\ \\&=&\dfrac{20}{\sqrt{5}}\\ \\&=&\dfrac{20\times\sqrt{5}}{(\sqrt{5})\times(\sqrt{5})}\\ \\&=&\dfrac{20\sqrt{5}}{5}\\ \\&=&4\sqrt{5}\end{array}$
Ainsi, $\boxed{CH=4\sqrt{5}\;cm}$
$-\ $ Calcul de $AH$
D'après la troisième relation métrique, on a :
$$AH^{2}=BH\times CH$$
Alors,
$\begin{array}{rcl} AH&=&\sqrt{BH\times CH}\\ \\&=&\sqrt{(\sqrt{5})\times(4\sqrt{5})}\\ \\&=&\sqrt{4(\sqrt{5})\times(\sqrt{5})}\\ \\&=&\sqrt{4\times 5}\\ \\&=&2\sqrt{5}\end{array}$
D'où, $\boxed{AH=2\sqrt{5}\;cm}$
4) Soit $B'\ $ et $\ C'$ respectivement les projetés orthogonaux des points $B\ $ et $\ C$ sur l'axe $(Oy)$
a) Calculons $\dfrac{BH}{BC}\ $ et $\ \dfrac{B'O}{B'C'}$
$-\ $ Calcul de $\dfrac{BH}{BC}$
On a :
$\begin{array}{rcl}\dfrac{BH}{BC}&=&\dfrac{\sqrt{5}}{5\sqrt{5}}\\ \\&=&\dfrac{1}{5}\end{array}$
Donc, $\boxed{\dfrac{BH}{BC}=\dfrac{1}{5}}$
$-\ $ Calcul de $\dfrac{B'O}{B'C'}$
Comme $B'\ $ et $\ C'$ sont respectivement les projetés orthogonaux des points $B\ $ et $\ C$ sur l'axe $(Oy)$ alors, on a :
$B'\begin{pmatrix} x_{B'}=0\\y_{B'}=y_{B}\end{pmatrix}=\begin{pmatrix} 0\\-2\end{pmatrix}$
$C'\begin{pmatrix} x_{C'}=0\\y_{C'}=y_{C}\end{pmatrix}=\begin{pmatrix} 0\\8\end{pmatrix}$
Par suite, en calculant la distance $B'O$, on trouve :
$\begin{array}{rcl} B'O&=&\left|y_{O}-y_{B'}\right|\\\\&=&\left|0-(-2)\right|\\\\&=&\left|2\right|\\\\&=&2\end{array}$
Donc, $\boxed{B'O=2\;cm}$
Aussi, la distance $B'C'$ est donnée par :
$\begin{array}{rcl} B'C'&=&\left|y_{C'}-y_{B'}\right|\\\\&=&\left|8-(-2)\right|\\\\&=&\left|8+2\right|\\\\&=&\left|10\right|\\\\&=&10\end{array}$
Alors, $\boxed{B'C'=10\;cm}$
Ainsi, en calculant $\dfrac{B'O}{B'C'}$, on obtient :
$\begin{array}{rcl}\dfrac{B'O}{B'C'}&=&\dfrac{2}{10}\\\\&=&\dfrac{1}{5}\end{array}$
D'où, $\boxed{\dfrac{B'O}{B'C'}=\dfrac{1}{5}}$
On remarque alors que :
$$\dfrac{BH}{BC}=\dfrac{B'O}{B'C'}=\dfrac{1}{5}$$
b) Montrons avec précision que l'on peut en conclure que $H$ appartient à l'axe $(Ox)$
Soit $B\;,\ H\;,\ C$ trois points alignés d'une part, et $B'\;,\ O\;,\ C'$ trois points alignés d'autre part, dans le même ordre.
Or, d'après le résultat de la question $4)\;a)$, on a :
$$\dfrac{BH}{BC}=\dfrac{B'O}{B'C'}$$
Donc, d'après la réciproque du théorème de Thalès, les droites $(BB')\ $ et $\ (OH)$ sont parallèles.
Par ailleurs, $(BB')\ $ et $\ (Ox)$ étant deux droites parallèles alors, toute droite parallèle à l'une est aussi parallèle à l'autre.
D'où, $(OH)$ parallèle à $(Ox).$
Comme $O$ appartient à l'axe $(Ox)$ alors, $(OH)\ $ et $\ (Ox)$ sont confondues.
Par conséquent, $H$ appartient à l'axe $(Ox).$
Exercice 5
Dans le plan muni d'un repère orthonormé $(O\;;\ \overrightarrow{OI}\;,\ \overrightarrow{OJ})$, on donne les points :
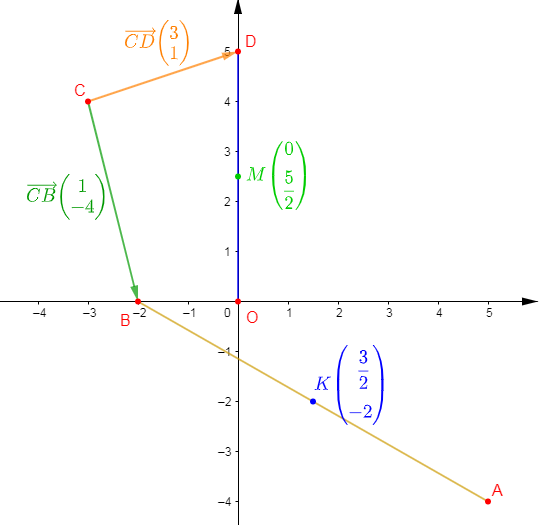
$$A(5\;;\ -4)\;,\ B(-2\;;\ 0)\;,\ C(-3\;;\ 4)\ \text{ et }\ D(0\;;\ 5)$$
1) Plaçons les points $A\;,\ B\;,\ C\ $ et $\ D.$
2) Calculons les coordonnées des points $K\ $ et $\ M$ milieux respectifs des segments $[AB]\ $ et $\ [DO].$
Soit $K$ le milieu du segment $[AB].$
Alors, les coordonnées de $K$ sont données par :
$$x_{K}=\dfrac{x_{A}+x_{B}}{2}\quad \text{et}\quad y_{K}=\dfrac{y_{A}+y_{B}}{2}$$
Ce qui donne : $x_{K}=\dfrac{5-2}{2}=\dfrac{3}{2}\quad$ et $\quad y_{K}=\dfrac{-4+0}{2}=-2$
D'où, $$\boxed{K\begin{pmatrix} \dfrac{3}{2}\\\\ -2\end{pmatrix}}$$
Soit $M$ le milieu du segment $[DO].$
Alors, les coordonnées de $M$ sont données par :
$$x_{M}=\dfrac{x_{D}+x_{O}}{2}\quad \text{et}\quad y_{M}=\dfrac{y_{D}+y_{O}}{2}$$
En calculant, on trouve : $x_{M}=\dfrac{0+0}{2}=0\ $ et $\ y_{M}=\dfrac{5+0}{2}=\dfrac{5}{2}$
Ainsi, $$\boxed{M\begin{pmatrix} 0\\\\ \dfrac{5}{2}\end{pmatrix}}$$
3) a) Calculons les coordonnées des vecteurs $\overrightarrow{CB}\ $ et $\ \overrightarrow{CD}.$
Les coordonnées du vecteur $\overrightarrow{CB}$ sont données par :
$$x_{_{\overrightarrow{CB}}}=x_{B}-x_{C}\quad \text{et}\quad y_{_{\overrightarrow{CB}}}=y_{B}-y_{C}$$
Soit alors :
$\begin{array}{rcl} x_{_{\overrightarrow{CB}}}&=&x_{B}-x_{C}\\\\&=&-2-(-3)\\\\&=&-2+3\\\\&=&1\end{array}$
Donc, $\boxed{x_{_{\overrightarrow{CB}}}=1}$
$\begin{array}{rcl} y_{_{\overrightarrow{CB}}}&=&y_{B}-y_{C}\\\\&=&0-4\\\\&=&-4\end{array}$
Ainsi, $\boxed{y_{_{\overrightarrow{CB}}}=-4}$
D'où, on a :
$$\boxed{\overrightarrow{CB}\begin{pmatrix} 1\\-4\end{pmatrix}}$$
Les coordonnées du vecteur $\overrightarrow{CD}$ sont données par :
$$x_{_{\overrightarrow{CD}}}=x_{D}-x_{C}\quad \text{et}\quad y_{_{\overrightarrow{CD}}}=y_{D}-y_{C}$$
Soit alors :
$\begin{array}{rcl} x_{_{\overrightarrow{CD}}}&=&x_{D}-x_{C}\\\\&=&0-(-3)\\\\&=&0+3\\\\&=&3\end{array}$
Donc, on trouve : $\boxed{x_{_{\overrightarrow{CD}}}=3}$
$\begin{array}{rcl} y_{_{\overrightarrow{CD}}}&=&y_{D}-y_{C}\\\\&=&5-4\\\\&=&1\end{array}$
On trouve alors : $\boxed{y_{_{\overrightarrow{CD}}}=1}$
Ainsi, on obtient :
$$\boxed{\overrightarrow{CD}\begin{pmatrix} 3\\1\end{pmatrix}}$$
b) En déduisons les distances $CB\ $ et $\ CD.$
Soit : $\overrightarrow{CB}\begin{pmatrix} 1\\-4\end{pmatrix}.$
Alors, la distance $CB$ est donnée par :
$\begin{array}{rcl} CB&=&\sqrt{(1)^{2}+(-4)^{2}}\\\\&=&\sqrt{1+16}\\\\&=&\sqrt{17}\end{array}$
Donc, $\boxed{CB=\sqrt{17}}$
Soit : $\overrightarrow{CD}\begin{pmatrix} 3\\1\end{pmatrix}.$
Alors, la distance $CD$ est donnée par :
$\begin{array}{rcl} CD&=&\sqrt{(3)^{2}+(1)^{2}}\\\\&=&\sqrt{9+1}\\\\&=&\sqrt{10}\end{array}$
D'où, $\boxed{CD=\sqrt{10}}$

Exercice 6
Dans le plan muni d'un repère orthonormé $(O\;;\ \overrightarrow{OI}\;,\ \overrightarrow{OJ})$, on donne les points :
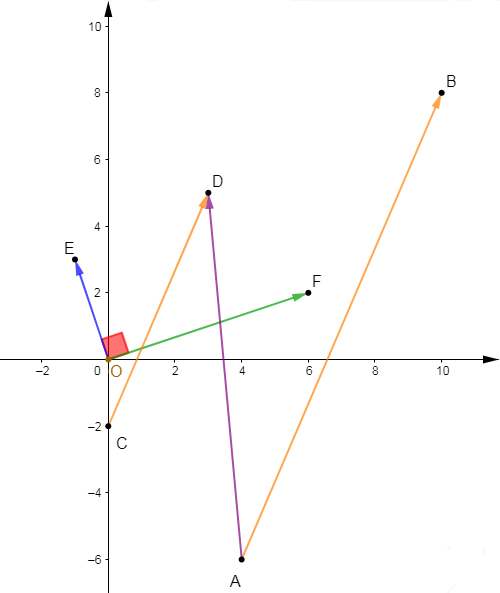
$E\begin{pmatrix} -1\\ 3\end{pmatrix}\;,\ F\begin{pmatrix} 6\\ 2\end{pmatrix}\;,\ A\begin{pmatrix} 4\\ -6\end{pmatrix}\;,\ B\begin{pmatrix} 10\\ 8\end{pmatrix}\;,\ C\begin{pmatrix} 0\\ -2\end{pmatrix}\ $ et $\ D\begin{pmatrix} 3\\ 5\end{pmatrix}$
1) Démontrons que les vecteurs $\overrightarrow{OE}\ $ et $\ \overrightarrow{OF}$ sont orthogonaux.
Calculons d'abord les coordonnées de ces deux vecteurs.
On a :
$\overrightarrow{OE}\begin{pmatrix} -1-0\\3-0\end{pmatrix}=\begin{pmatrix} -1\\3\end{pmatrix}$
$\overrightarrow{OF}\begin{pmatrix} 6-0\\2-0\end{pmatrix}=\begin{pmatrix} 6\\2\end{pmatrix}$
Puis, vérifions la condition d'orthogonalité.
On obtient alors :
$\begin{array}{rcl} (x_{_{\overrightarrow{OE}}}\times x_{_{\overrightarrow{OF}}})+(y_{_{\overrightarrow{OE}}}\times y_{_{\overrightarrow{OF}}})&=&(-1\times 6)+(3\times 2)\\\\&=&-6+6\\\\&=&0\end{array}$
Donc, $\boxed{(x_{_{\overrightarrow{OE}}}\times x_{_{\overrightarrow{OF}}})+(y_{_{\overrightarrow{OE}}}\times y_{_{\overrightarrow{OF}}})=0}$
Ce qui signifie que les coordonnées des vecteurs $\overrightarrow{OE}\ $ et $\ \overrightarrow{OF}$ vérifient la condition d'orthogonalité.
Par conséquent, les vecteurs $\overrightarrow{OE}\ $ et $\ \overrightarrow{OF}$ sont orthogonaux.
2) Démontrons que les vecteurs $\overrightarrow{AB}\ $ et $\ \overrightarrow{CD}$ sont colinéaires.
Calculons d'abord les coordonnées de ces deux vecteurs.
On a alors :
$\overrightarrow{AB}\begin{pmatrix} 10-4\\8-(-6)\end{pmatrix}=\begin{pmatrix} 6\\14\end{pmatrix}$
$\overrightarrow{CD}\begin{pmatrix} 3-0\\5-(-2)\end{pmatrix}=\begin{pmatrix} 3\\7\end{pmatrix}$
Puis, vérifions la condition de colinéarité.
Ce qui donne alors :
$\begin{array}{rcl} (x_{_{\overrightarrow{AB}}}\times y_{_{\overrightarrow{CD}}})-(x_{_{\overrightarrow{CD}}}\times y_{_{\overrightarrow{AB}}})&=&(6\times 7)-(3\times 14)\\\\&=&42-42\\\\&=&0\end{array}$
Donc, $\boxed{(x_{_{\overrightarrow{AB}}}\times y_{_{\overrightarrow{CD}}})-(x_{_{\overrightarrow{CD}}}\times y_{_{\overrightarrow{AB}}})=0}$
Ce qui signifie que les coordonnées des vecteurs $\overrightarrow{AB}\ $ et $\ \overrightarrow{Cd}$ vérifient la condition de colinéarité.
Par conséquent, les vecteurs $\overrightarrow{AB}\ $ et $\ \overrightarrow{CD}$ sont colinéaires.
3) $\overrightarrow{OE}$ n'est pas égal à $\overrightarrow{AD}.$
Justifions notre réponse.
En effet, en calculant les coordonnées des vecteurs $\overrightarrow{OE}\ $ et $\ \overrightarrow{AD}$, on obtient :
$\overrightarrow{AD}\begin{pmatrix} 3-4\\5-(-6)\end{pmatrix}=\begin{pmatrix} -1\\11\end{pmatrix}$
$\overrightarrow{OE}\begin{pmatrix} 1\\3\end{pmatrix}$
On remarque alors que ces deux vecteurs n'ont pas les mêmes coordonnées.
Par conséquent, ils ne sont pas égaux.

Exercice 7
Le plan est muni d'un repère orthonormé $(O\;;\ \overrightarrow{OI}\;,\ \overrightarrow{OJ}).$
1) Soient $\overrightarrow{AB}\begin{pmatrix} 5+x \\ 3\end{pmatrix}\ $ et $\ \overrightarrow{CD}\begin{pmatrix} 1 \\ 2y-3\end{pmatrix}.$
Calculons $x\ $ et $\ y$ pour que ces deux vecteurs soient égaux.
En effet, on sait que deux vecteurs sont égaux s'ils ont les mêmes coordonnées.
Ainsi, on a :
$\begin{array}{rcl}\overrightarrow{AB}=\overrightarrow{CD}&\Leftrightarrow&\left\lbrace\begin{array}{rcl} 5+x&=&1\\\\ 3&=&2y-3\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl}x&=&1-5\\\\ 3+3&=&2y\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl}x&=&-4\\\\ 6&=&2y\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl}x&=&-4\\\\ y&=&\dfrac{6}{2}\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl}x&=&-4\\\\ y&=&3\end{array}\right.\end{array}$
D'où, $\boxed{x=-4\ \text{ et }\ y=3}$
2) Soient $\overrightarrow{OE}\begin{pmatrix} 7 \\ 3x+2\end{pmatrix}\ $ et $\ \overrightarrow{OF}\begin{pmatrix} 2 \\ 3-x\end{pmatrix}.$
Calculons $x$ pour que ces deux vecteurs soient colinéaires.
En effet, on sait que deux vecteurs sont colinéaires si, et seulement si, leurs coordonnées vérifient la condition de colinéarité.
Donc, on a :
$\begin{array}{rcl}\overrightarrow{OE}\ \text{ et }\ \overrightarrow{OF}\ \text{ sont colinéaires}&\Leftrightarrow&[7\times(3-x)]-[2\times(3x+2)]=0\\\\&\Leftrightarrow&21-7x-6x-4=0\\\\&\Leftrightarrow&17-13x=0\\\\&\Leftrightarrow&-13x=-17\\\\&\Leftrightarrow&x=\dfrac{-17}{-13}\\\\&\Leftrightarrow&x=\dfrac{17}{13}\end{array}$
D'où, $\boxed{x=\dfrac{17}{13}}$
3) Soient $\overrightarrow{BE}\begin{pmatrix} 3 \\ x+3\end{pmatrix}\ $ et $\ \overrightarrow{MF}\begin{pmatrix} \dfrac{2}{3}-2x \\ \\ -4\end{pmatrix}.$
Calculons $x$ pour que ces deux vecteurs soient orthogonaux.
En effet, on sait que deux vecteurs sont orthogonaux si, et seulement si, leurs coordonnées vérifient la condition d'orthogonalité.
Donc, en appliquant cette propriété, on obtient :
$\begin{array}{rcl}\overrightarrow{BE}\ \text{ et }\ \overrightarrow{MF}\ \text{ sont orthogonaux}&\Leftrightarrow&\left[3\times\left(\dfrac{2}{3}-2x\right)\right]+[(x+3)\times(-4)]=0\\\\&\Leftrightarrow&2-6x-4x-12=0\\\\&\Leftrightarrow&-10x-10=0\\\\&\Leftrightarrow&-10x=10\\\\&\Leftrightarrow&x=\dfrac{10}{-10}\\\\&\Leftrightarrow&x=-1\end{array}$
Ainsi, $\boxed{x=-1}$
4) On considère les points $A\;,\ B$ et $C$, tels que : $\overrightarrow{OA}(4\;;\ 2)\;;\ \overrightarrow{AB}(-4\;;\ 4)\ $ et $\ \overrightarrow{BC}(-2\;;\ -2).$
Calculons les coordonnées des points $A\;,\ B\ $ et $\ C.$
En effet, comme $O$ est l'origine du repère alors, les coordonnées du vecteur $\overrightarrow{OA}$ sont les mêmes que celles du point $A.$
Donc,
$$\boxed{A\begin{pmatrix} 4\\2\end{pmatrix}}$$
Pour trouver les coordonnées du point $B$, on peut d'abord utiliser la relation de Chasles.
Ainsi, on a :
$$\overrightarrow{OA}+\overrightarrow{AB}=\overrightarrow{OB}$$
Puis, en faisant la somme des coordonnées des vecteurs $\overrightarrow{OA}\ $ et $\ \overrightarrow{AB}$, on obtient les coordonnées de $B.$
Soit alors :
$\overrightarrow{OB}\begin{pmatrix} 4-4\\2+4\end{pmatrix}=\begin{pmatrix} 0\\6\end{pmatrix}$
Comme $O$ est l'origine du repère alors, le vecteur $\overrightarrow{OB}$ et le point $B$ ont les mêmes coordonnées.
D'où,
$$\boxed{B\begin{pmatrix} 0\\6\end{pmatrix}}$$
De la même manière, d'après Chasles, on a :
$$\overrightarrow{OB}+\overrightarrow{BC}=\overrightarrow{OC}$$
Ainsi, les coordonnées de $\overrightarrow{OC}$ sont données par :
$\overrightarrow{OC}\begin{pmatrix} 0-2\\6-2\end{pmatrix}=\begin{pmatrix} -2\\4\end{pmatrix}$
Comme $O$ est l'origine du repère alors, le vecteur $\overrightarrow{OC}$ et le point $C$ ont les mêmes coordonnées.
D'où,
$$\boxed{C\begin{pmatrix} -2\\4\end{pmatrix}}$$
Exercice 8
Le plan est muni d'un repère orthonormé $\left(O\;;\ \overrightarrow{OI}\;,\ \overrightarrow{OJ}\right).$
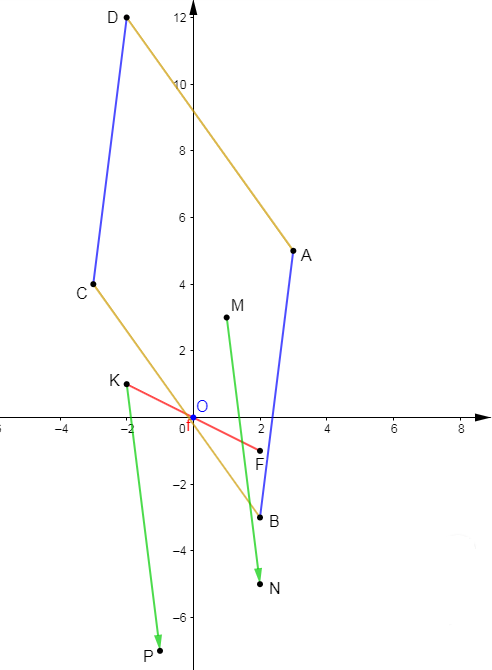
1) On donne les points : $A\begin{pmatrix} 3\\ 5\end{pmatrix}\;,\ B\begin{pmatrix} 2\\ -3\end{pmatrix}\ $ et $\ C\begin{pmatrix} -3\\ 4\end{pmatrix}.$
Trouvons les coordonnées de $D$ pour que $ABCD$ soit un parallélogramme.
En effet, $ABCD$ est un parallélogramme alors, on a :
$$\overrightarrow{AD}=\overrightarrow{BC}.$$
Or, on sait que deux vecteurs sont égaux lorsqu'ils ont les mêmes coordonnées.
Soit alors :
$\overrightarrow{AD}\begin{pmatrix} x_{D}-3\\ y_{D}-5\end{pmatrix}$
$\overrightarrow{BC}\begin{pmatrix} -3-2\\ 4-(-3)\end{pmatrix}=\begin{pmatrix} -5\\ 7\end{pmatrix}$
Ainsi, on a :
$\begin{array}{rcl}\overrightarrow{AD}=\overrightarrow{BC}&\Leftrightarrow&\left\lbrace\begin{array}{rcl}x_{D}-3&=&-5\\\\y_{D}-5&=&7\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl}x_{D}&=&-5+3\\\\y_{D}&=&7+5\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl}x_{D}&=&-2\\\\y_{D}&=&12\end{array}\right.\end{array}$
D'où, $$\boxed{D\begin{pmatrix} -2\\ 12\end{pmatrix}}$$
2) On donne les points : $K\begin{pmatrix} -2\\ 1\end{pmatrix}\;,\ M\begin{pmatrix} 1\\ 3\end{pmatrix}\ $ et $\ N\begin{pmatrix} 2\\ -5\end{pmatrix}.$
Trouvons les coordonnées de $P$ image de $K$ par la translation de vecteur $\overrightarrow{MN}.$
On a : $t_{_{\overrightarrow{MN}}}(K)=P.$
Ce qui signifie que :
$$\overrightarrow{KP}=\overrightarrow{MN}$$
Or, on sait que deux vecteurs sont égaux lorsqu'ils ont les mêmes coordonnées.
Soit alors :
$\overrightarrow{KP}\begin{pmatrix} x_{P}-(-2)\\ y_{P}-1\end{pmatrix}=\begin{pmatrix} x_{P}+2\\ y_{P}-1\end{pmatrix}$
$\overrightarrow{MN}\begin{pmatrix} 2-1\\ -5-3\end{pmatrix}=\begin{pmatrix} 1\\ -8\end{pmatrix}$
Donc, on a :
$\begin{array}{rcl}\overrightarrow{KP}=\overrightarrow{MN}&\Leftrightarrow&\left\lbrace\begin{array}{rcl}x_{P}+2&=&1\\\\y_{P}-1&=&-8\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl}x_{P}&=&1-2\\\\y_{P}&=&-8+1\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl}x_{P}&=&-1\\\\y_{P}&=&-7\end{array}\right.\end{array}$
Ainsi, $$\boxed{P\begin{pmatrix} -1\\ -7\end{pmatrix}}$$
3) Trouvons les coordonnées de $F$ symétrique de $K$ par rapport à $O.$
En effet, comme $F$ est le symétrique de $K$ par rapport à $O$ alors, $O$ est milieu du segment $[KF]$ et on a :
$$\overrightarrow{OF}=\overrightarrow{KO}$$
Or, on sait que deux vecteurs sont égaux lorsqu'ils ont les mêmes coordonnées.
Soit alors :
$\overrightarrow{OF}\begin{pmatrix} x_{F}-0\\ y_{F}-0\end{pmatrix}=\begin{pmatrix} x_{F}\\ y_{F}\end{pmatrix}$
$\overrightarrow{KO}\begin{pmatrix} 0-(-2)\\ 0-1\end{pmatrix}=\begin{pmatrix} 2\\ -1\end{pmatrix}$
Ainsi, on a :
$\begin{array}{rcl}\overrightarrow{OF}=\overrightarrow{KO}&\Leftrightarrow&\left\lbrace\begin{array}{rcl}x_{F}&=&2\\\\y_{F}&=&-1\end{array}\right.\end{array}$
D'où, $$\boxed{F\begin{pmatrix} 2\\ -1\end{pmatrix}}$$

Exercice 9
Le plan est muni d'un repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j})$, On donne les points $A\;,\ B\ $ et $\ C$ tels que :
$$\overrightarrow{OA}=6\vec{i}-\vec{j}\;;\ \overrightarrow{OB}=2\vec{i}-2\vec{j}\ \text{ et }\ \overrightarrow{OC}=5\vec{i}+3\vec{j}$$
1) Plaçons les points $A\;,\ B\;,\ C.$
Pour cela, déterminons leurs coordonnées d'une autre manière.
On a :
$\overrightarrow{OA}=6\vec{i}-\vec{j}$ alors, $A\begin{pmatrix} 6\\ -1\end{pmatrix}$
$\overrightarrow{OB}=2\vec{i}-2\vec{j}$ donc, $B\begin{pmatrix} 2\\ -2\end{pmatrix}$
$\overrightarrow{OC}=5\vec{i}+3\vec{j}$ alors, $C\begin{pmatrix} 5\\ 3\end{pmatrix}$
Montrons que $\overrightarrow{AB}\ $ et $\ \overrightarrow{AC}$ sont orthogonaux.
Calculons d'abord les coordonnées de ces deux vecteurs.
On a :
$\overrightarrow{AB}\begin{pmatrix} 2-6\\-2-(-1)\end{pmatrix}=\begin{pmatrix} -4\\-1\end{pmatrix}$
$\overrightarrow{AC}\begin{pmatrix} 5-6\\3-(-1)\end{pmatrix}=\begin{pmatrix} -1\\4\end{pmatrix}$
Puis, vérifions la condition d'orthogonalité.
On obtient alors :
$\begin{array}{rcl} (x_{_{\overrightarrow{AB}}}\times x_{_{\overrightarrow{AC}}})+(y_{_{\overrightarrow{AB}}}\times y_{_{\overrightarrow{AC}}})&=&(-4\times(-1))+((-1)\times 4)\\\\&=&4-4\\\\&=&0\end{array}$
Donc, $\boxed{(x_{_{\overrightarrow{AB}}}\times x_{_{\overrightarrow{AC}}})+(y_{_{\overrightarrow{AB}}}\times y_{_{\overrightarrow{AC}}})=0}$
Ce qui signifie que les coordonnées des vecteurs $\overrightarrow{AB}\ $ et $\ \overrightarrow{AC}$ vérifient la condition d'orthogonalité.
Par conséquent, les vecteurs $\overrightarrow{AB}\ $ et $\ \overrightarrow{AC}$ sont orthogonaux.
2) Calculer les distances $AB\;,\ CB\ $ et $\ AC.$
Soit : $\overrightarrow{AB}\begin{pmatrix} -4\\-1\end{pmatrix}$ alors, on a :
$\begin{array}{rcl} AB&=&\sqrt{(-4)^{2}+(-1)^{2}}\\\\&=&\sqrt{16+1}\\\\&=&\sqrt{17}\end{array}$
Donc, $\boxed{AB=\sqrt{17}}$
Soit : $\overrightarrow{CB}\begin{pmatrix} 2-5\\-2-3\end{pmatrix}=\begin{pmatrix} -3\\-5\end{pmatrix}$ alors, on a :
$\begin{array}{rcl} CB&=&\sqrt{(-3)^{2}+(-5)^{2}}\\\\&=&\sqrt{9+25}\\\\&=&\sqrt{34}\end{array}$
D'où, $\boxed{CB=\sqrt{34}}$
Soit : $\overrightarrow{AC}\begin{pmatrix} -1\\4\end{pmatrix}$ alors, on a :
$\begin{array}{rcl} AC&=&\sqrt{(-1)^{2}+(4)^{2}}\\\\&=&\sqrt{1+16}\\\\&=&\sqrt{17}\end{array}$
Ainsi, $\boxed{AC=\sqrt{17}}$
En déduisons la nature du triangle $ABC.$
D'après ce qui précède, on a :
$AB^{2}=(\sqrt{17})^{2}=17$
$AC^{2}=(\sqrt{17})^{2}=17$
$CB^{2}=(\sqrt{34})^{2}=34$
Alors, on constate que : $17+17=34$
Ce qui signifie que : $AB^{2}+AC^{2}=CB^{2}.$
Ainsi, d'après la réciproque du théorème de Pythagore $ABC$ est un triangle rectangle en $A.$
De plus, on a : $AB=AC.$
Par conséquent, le triangle $ABC$ est rectangle isocèle en $A.$
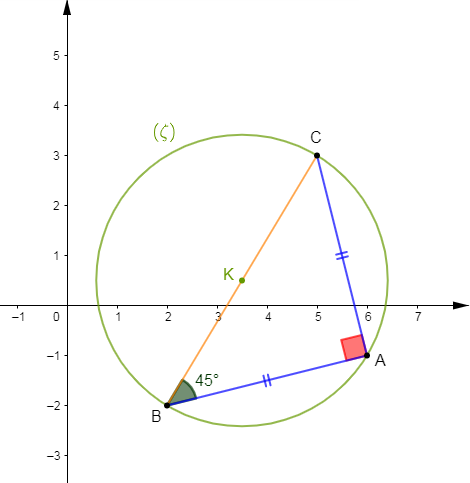
3) Calculons les coordonnées du centre $K$ du cercle $(\zeta)$ circonscrit à $ABC.$
Comme $ABC$ est rectangle en $A$ alors, le centre $K$ du cercle circonscrit est le milieu de l'hypoténuse $[CB].$
Donc, les coordonnées de $K$ sont données par :
$$x_{K}=\dfrac{x_{C}+x_{B}}{2}\quad\text{et}\quad y_{K}=\dfrac{y_{C}+y_{B}}{2}$$
Par suite :
$x_{K}=\dfrac{5+2}{2}=\dfrac{7}{2}$
$y_{K}=\dfrac{3-2}{2}=\dfrac{1}{2}$
Ainsi,
$$\boxed{K\begin{pmatrix}\dfrac{7}{2}\\ \\\dfrac{1}{2}\end{pmatrix}}$$
Traçons $(\zeta)$ puis calculons son rayon.
On sait que $[CB]$ est un diamètre pour le cercle $(\zeta).$
Donc, le rayon $r$ de ce cercle est donné par : $r=\dfrac{CB}{2}$
Ainsi, $\boxed{r=\dfrac{\sqrt{34}}{2}}$
4) Calculer le sinus et la tangente de l'angle $\widehat{ABC}.$
Comme le triangle $ABC$ est rectangle en $A$ alors, $\sin\widehat{ABC}$ est donnée par :
$$\sin\widehat{ABC}=\dfrac{\text{côté opposé à l'angle }\widehat{ABC}}{\text{hypoténuse}}$$
Donc, on a :
$\begin{array}{rcl}\sin\widehat{ABC}&=&\dfrac{AC}{CB}\\\\&=&\dfrac{\sqrt{17}}{\sqrt{34}}\\\\&=&\dfrac{\sqrt{17}}{\sqrt{2}\times\sqrt{17}}\\\\&=&\dfrac{1}{\sqrt{2}}\\\\&=&\dfrac{\sqrt{2}}{\sqrt{2}\times\sqrt{2}}\\\\&=&\dfrac{\sqrt{2}}{2}\end{array}$
D'où, $\boxed{\sin\widehat{ABC}=\dfrac{\sqrt{2}}{2}}$
Comme le triangle $ABC$ est rectangle en $B$ alors, $\tan\widehat{ABC}$ est donnée par :
$$\tan\widehat{ABC}=\dfrac{\text{côté opposé à l'angle }\widehat{ABC}}{\text{côté adjacent à l'angle }\widehat{ABC}}$$
Ainsi, on a :
$\begin{array}{rcl}\tan\widehat{ABC}&=&\dfrac{AC}{AB}\\\\&=&\dfrac{\sqrt{17}}{\sqrt{17}}\\\\&=&1\end{array}$
D'où, $\boxed{\tan\widehat{ABC}=1}$
En déduisons la mesure de l'angle $\widehat{ABC}.$
On sait que : $\sin 45^{\circ}=\dfrac{\sqrt{2}}{2}\ $ et $\ \tan 45^{\circ}=1$
Par conséquent, $\boxed{mes\;\widehat{ABC}=45^{\circ}}$

Exercice 10
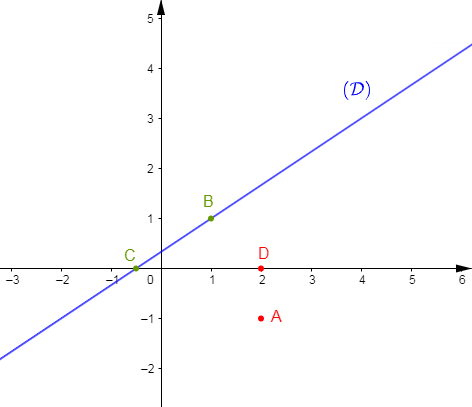
1) Trouvons l'équation réduite de la droite $(D)$ passant par $A(1\;;\ 1)$ et de coefficient directeur $2.$
Une équation réduite de la droite $(D)$ passant par $A(1\;;\ 1)$ et de coefficient directeur $2$ est de la forme :
$$(D)\ :\ y=2x+b$$
Or, on sait que $(D)$ passe par $A(1\;;\ 1)$ donc, les coordonnées de ce point vérifient l'équation réduite de $(D).$
Ce qui se traduit par : $1=2+b\ \Rightarrow\ b=1-2=-1$
Ainsi, une équation réduite de la droite $(D)$ passant par $A(1\;;\ 1)$ et de coefficient directeur $2$ est donnée par :
$$\boxed{(D)\ :\ y=2x-1}$$
2) Soit $(D')\ :\ 2y+x-3=0.$ Justifions que $(D)\ $ et $\ (D')$ sont perpendiculaires.
En effet, on peut écrire : $(D')\ :\ x+2y-3=0$
Donc, $\vec{u}\begin{pmatrix} -2\\1\end{pmatrix}$ est un vecteur directeur de $(D').$
Par suite, son coefficient directeur $a'$ est donné par :
$$a'=\dfrac{1}{-2}$$
Alors, en faisant le produit des coefficients directeurs des droites $(D)\ $ et $\ (D')$, on trouve :
$$2\times\left(\dfrac{1}{-2}\right)=\dfrac{2}{-2}=-1$$
Ainsi, on remarque que les coefficients directeurs de ces deux droites vérifient la condition d'orthogonalité.
Par conséquent, les droites $(D)\ $ et $\ (D')$ sont perpendiculaires.
Exercice 11
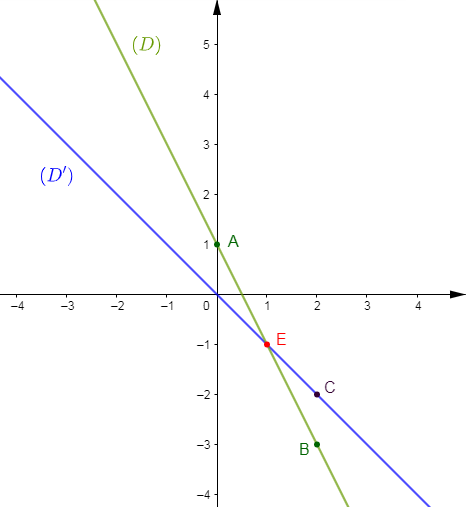
Soient $(D)\ :\ -2x+y-1=0\ $ et $\ (D')\ :\ y=-\dfrac{1}{2}x+b$
1) Justifions que $(D)\ $ et $\ (D')$ sont perpendiculaires.
On a : $(D)\ :\ -2x+y-1=0$
Alors, $\vec{v}\begin{pmatrix} -1\\-2\end{pmatrix}$ est un vecteur directeur de $(D).$
Son coefficient directeur $a$ est donc donné par :
$$a=\dfrac{-2}{-1}=2$$
Par ailleurs, on sait que le coefficient directeur de $(D')$ est égal à $-\dfrac{1}{2}$
Donc, en faisant le produit des coefficients directeurs des droites $(D)\ $ et $\ (D')$, on trouve :
$$2\times\left(-\dfrac{1}{2}\right)=-\dfrac{2}{2}=-1$$
Ainsi, on remarque alors les coefficients directeurs de ces deux droites vérifient la condition d'orthogonalité.
Par conséquent, les droites $(D)\ $ et $\ (D')$ sont perpendiculaires.
2) Calculons le réel $b$ pour que la droite $(D')$ passe par le point $A(2\;;\ 3).$
Pour cela, on remplace les coordonnées de $A$ dans l'équation de $(D').$
On obtient alors :
$\begin{array}{rcl} -\dfrac{1}{2}\times 2+b=3&\Rightarrow&-\dfrac{2}{2}+b=3\\\\&\Rightarrow&-1+b=3\\\\&\Rightarrow&b=3+1\\\\&=&b=4\end{array}$
D'où, $\boxed{b=4}$
Exercice 12
Soient les vecteurs $\vec{u}(a\;;\ b)\ $ et $\ \vec{v}(a'\;;\ b')$ dans le plan muni d'un repère orthonormal $(O;\ \vec{i},\ \vec{j}).$
1) Indiquons une relation entre $a\;;\ b\;;\ a'\ $ et $\ b'$ traduisant la colinéarité des vecteurs $\vec{u}\ $ et $\ \vec{v}.$
Les vecteurs $\vec{u}\ $ et $\ \vec{v}$ sont colinéaires si, et seulement si :
$$\boxed{a\times b'-a'\times b=0}$$
2) On donne : $\vec{u}\begin{pmatrix} x-1\\-3\end{pmatrix}\ $ et $\ \vec{v}\begin{pmatrix} -3\\2\end{pmatrix}.$ Déterminons $x$ pour que $\vec{u}\ $ et $\ \vec{v}$ soient colinéaires.
En appliquant la condition de colinéarité, on obtient :
$\begin{array}{rcl}\vec{u}\ \text{ et }\ \vec{v}\ \text{ sont colinéaires}&\Leftrightarrow&[(x-1)\times 2]-[(-3)\times(-3)]=0\\\\&\Leftrightarrow&2x-2-9=0\\\\&\Leftrightarrow&2x-11=0\\\\&\Leftrightarrow&2x=11\\\\&\Leftrightarrow&x=\dfrac{11}{2}\end{array}$
D'où, $\boxed{x=\dfrac{11}{2}}$
Exercice 13
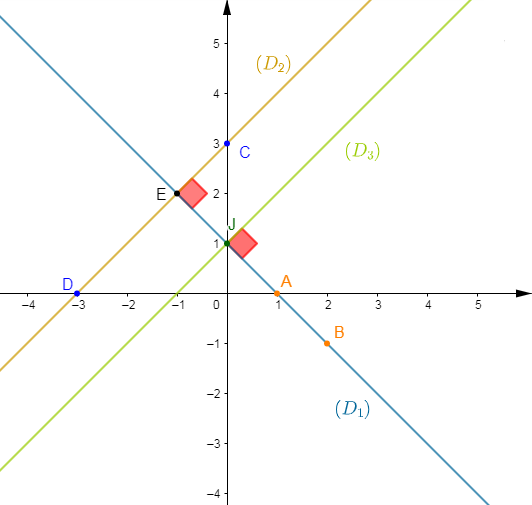
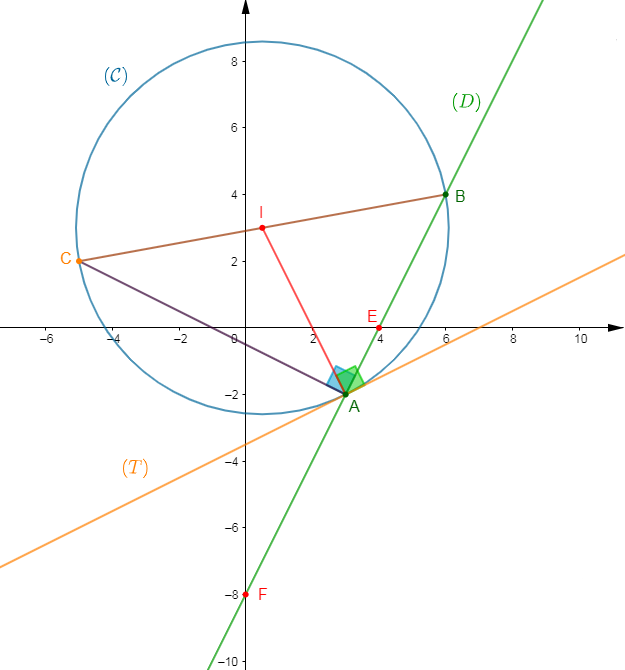
Dans le plan muni d'un repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j})$, on considère les droites $(D_{1})\ :\ y=-x+1\ $ et $\ (D_{2})\ :\ x-y+3=0.$
1) Démontrons que les droites $(D_{1})\ $ et $\ (D_{2})$ sont perpendiculaires.
On a : $(D_{1})\ :\ y=-x+1$ donc, le coefficient directeur $a_{1}$ de la droite $(D_{1})$ est égal à $-1$
Soit $(D_{2})\ :\ x-y+3=0$ alors, $\vec{w}\begin{pmatrix} 1\\1\end{pmatrix}$ est un vecteur directeur de $(D_{2}).$
Donc, le coefficient directeur $a_{2}$ de la droite $(D_{2})$ est donné par :
$$a_{2}=\dfrac{1}{1}=1$$
Ainsi, en faisant le produit des coefficients directeurs des droites $(D_{1})\ $ et $\ (D_{2})$, on trouve :
$$a_{1}\times a_{2}=-1\times 1=-1$$
Ce qui montre que les coefficients directeurs de ces deux droites vérifient bien la condition d'orthogonalité.
Par conséquent, les droites $(D_{1})\ $ et $\ (D_{2})$ sont perpendiculaires.
2) a) Construisons les droites $(D_{1})\ $ et $\ (D_{2}).$
$-\ $ Construction de $(D_{1})$
Choisissons deux points $A\ $ et $\ B$ dont les coordonnées vérifient l'équation de $(D_{1}).$
On a :
si $x=1$ alors, $y=0$
si $x=2$ alors, $y=-1$
Donc, plaçons les points $A\begin{pmatrix} 1\\0\end{pmatrix}\ $ et $\ B\begin{pmatrix} 2\\-1\end{pmatrix}$ puis, traçons la droite passant par $A\ $ et $\ B.$ C'est la droite $(D_{1}).$
$-\ $ Construction de $(D_{2})$
De la même manière, choisissons deux points $C\ $ et $\ D$ dont les coordonnées vérifient l'équation de $(D_{2}).$
On a :
si $x=0$ alors, $y=3$
si $x=-3$ alors, $y=0$
Plaçons alors les points $C\begin{pmatrix} 0\\3\end{pmatrix}\ $ et $\ D\begin{pmatrix} -3\\0\end{pmatrix}$ puis, traçons la droite passant par $C\ $ et $\ D.$ C'est la droite $(D_{2}).$
b) Justifions par le calcul que le point $J$ appartient à la droite $(D_{1}).$
On sait que le point $J$ appartient à la droite $(D_{1})$ si, et seulement si, ses coordonnées vérifient l'équation de $(D_{1}).$
Soit : $J\begin{pmatrix} 0\\1\end{pmatrix}.$
Alors, en remplaçant les coordonnées de $J$ dans l'équation de $(D_{1})$, on obtient :
$$1=-0+1=1$$
Cette relation est toujours vraie.
Ce qui signifie que les coordonnées de $J$ vérifient bien l'équation de $(D_{1}).$
Par conséquent, le point $J$ appartient à la droite $(D_{1}).$
c) On appelle $E$ le point d'intersection de $(D_{1})\ $ et $\ (D_{2}).$ Justifions par le calcul que $E$ a pour couple de coordonnées $(-1\;;\ 2 ).$
En effet, comme $E$ est le point d'intersection de $(D_{1})\ $ et $\ (D_{2})$ alors, ses coordonnées sont solutions du système d'équations formé par les équations respectives des droites $(D_{1})\ $ et $\ (D_{2}).$
Soit alors, à résoudre le système suivant :
$$\left\lbrace\begin{array}{rclr}y&=&-x+1&\quad(1)\\\\x-y+3&=&0&\quad(2)\end{array}\right.$$
Par substitution, on remplace $y$ dans l'équation $(2)$ par son expression dans l'équation $(1).$
On obtient alors :
$\begin{array}{rcl}x-(-x+1)+3=0&\Rightarrow&x+x-1+3=0\\\\&\Rightarrow&2x+2=0\\\\&\Rightarrow&2x=-2\\\\&\Rightarrow&x=\dfrac{-2}{2}\\\\&\Rightarrow&x=-1\end{array}$
Donc, $\boxed{x=-1}$
Ensuite, en remplaçant cette valeur de $x$ dans l'équation $(1)$, on trouve :
$y=-(-1)+1=1+1=2$
Donc, $\boxed{y=2}$
D'où, $S=\left\lbrace(-1\;;\ 2)\right\rbrace$
Ce qui justifie ben que $E$ a pour couple de coordonnées $(-1\;;\ 2 ).$
d) Calculons la distance $EJ.$
Soit : $\overrightarrow{EJ}\begin{pmatrix} 0-(-1)\\1-2\end{pmatrix}=\begin{pmatrix} 1\\-1\end{pmatrix}.$
Alors, on a :
$\begin{array}{rcl} EJ&=&\sqrt{(1)^{2}+(-1)^{2}}\\\\&=&\sqrt{1+1}\\\\&=&\sqrt{2}\end{array}$
D'où, $\boxed{EJ=\sqrt{2}}$
e) Déterminons une équation de la droite $(D_{3})$ passant par $J$ et parallèle à $(D_{2}).$
En effet, une équation de la droite $(D_{3})$ peut se mettre sous la forme :
$$y=ax+b$$
avec, $a$ le coefficient directeur et $b$ l'ordonnée à l'origine.
Comme $(D_{3})$ est parallèle à $(D_{2})$ alors, cela signifie que ces deux droites ont même coefficient directeur.
Or, on sait que le coefficient directeur de $(D_{2})$ est égal à $1.$
Par conséquent, celui de $(D_{2})$ est aussi égal à $1.$
D'où, $\boxed{a=1}$
Par suite, une équation réduite de la droite $(D_{3})$ est de la forme :
$$y=x+b$$
Par ailleurs, on sait que $(D_{3})$ passe par $J.$ Donc, les coordonnées de ce point vérifient l'équation réduite de $(D_{3}).$
Ainsi, en remplaçant dans cette équation les coordonnées de $J$, on trouve $b.$
Soit alors :
$\begin{array}{rcl} y_{J}=x_{J}+b&\Leftrightarrow&1=0+b\\\\&\Leftrightarrow&b=1\end{array}$
Ainsi, $\boxed{b=1}$
D'où, une équation de la droite $(D_{3})$ passant par $J$ et parallèle à $(D_{2})$ est donnée par :
$$\boxed{(D_{3})\ :\ y=x+1}$$
f) $(D_{3})\ $ et $\ (D_{1})$ sont perpendiculaires.
Justifions notre réponse.
En effet, d'après le résultat de la question $1)$, on a : $(D_{2})$ perpendiculaire à $(D_{1}).$
De plus, on a : $(D_{3})$ parallèle à $(D_{2}).$
Or, on sait que : si deux droites sont perpendiculaires alors, toute droite parallèle à l'une est perpendiculaire à l'autre.
Par conséquent, d'après cette propriété, $(D_{3})$ est perpendiculaire à $(D_{1}).$

Exercice 14
Le plan est rapporté à un repère orthonormal $(O\;;\ \vec{i}\;;\ \vec{j}).$
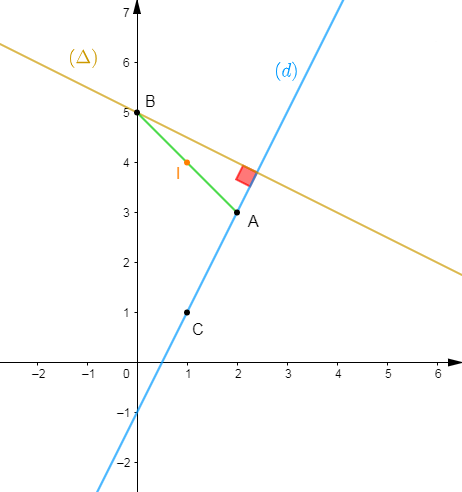
On donne la droite $(d)$ d'équation $y=2x-1$ ; le point $A$ de coordonnées $(2\;;\ 3)$ et le point $B$ de coordonnées $(0\;;\ 5).$
1) Plaçons les points $A\ $ et $\ B.$
2) Montrons que le point $A$ est sur la droite $(d).$
On sait que $A$ sur la droite $(d)$ si, et seulement si, ses coordonnées vérifient l'équation de $(d).$
Ainsi, dans l'équation de $(d)$, remplaçons $x\ $ et $\ y$ par les coordonnées du point $A.$
On obtient :
$\begin{array}{rcl} 3&=&2\times 2-1\\\\&=&4-1\\\\&=&3\end{array}$
On trouve alors, $3=3$ ; ce qui est toujours vrai.
Donc, les coordonnées de $A$ vérifient bien l'équation de $(d).$
Par conséquent, le point $A$ est sur la droite $(d).$
3) Construisons la droite $(d).$
D'après le résultat de la question $2)$, on sait que $(d)$ passe par $A.$
Donc, choisissons un deuxième point $C$ dont les coordonnées vérifient aussi l'équation de $(d).$
On a :
si $x=1$ alors, $y=1$
Alors, $C(1\;;\ 1)$ appartient aussi à la droite $(d).$
Plaçons ensuite le point $C$ puis, traçons la droite passant par $A\ $ et $\ C.$ C'est la droite $(d).$
4) Calculons :
a) les coordonnées du milieu $I$ de $[AB]$ ;
Les coordonnées de $I$ sont données par :
$$x_{I}=\dfrac{x_{A}+x_{B}}{2}\quad \text{et}\quad y_{I}=\dfrac{y_{A}+y_{B}}{2}$$
Soit alors : $x_{I}=\dfrac{2+0}{2}=\dfrac{2}{2}=1\quad$ et $\quad y_{I}=\dfrac{3+5}{2}=\dfrac{8}{2}=4$
Donc, $$\boxed{I\begin{pmatrix} 1\\4\end{pmatrix}}$$
b) les coordonnées du vecteur $\overrightarrow{AB}$ ;
Les coordonnées du vecteur $\overrightarrow{AB}$ sont données par :
$$x_{_{\overrightarrow{AB}}}=x_{B}-x_{A}\quad \text{et}\quad y_{_{\overrightarrow{AB}}}=y_{B}-y_{A}$$
Soit alors :
$\begin{array}{rcl} x_{_{\overrightarrow{AB}}}&=&x_{B}-x_{A}\\\\&=&0-2\\\\&=&-2\end{array}$
Donc, on trouve : $\boxed{x_{_{\overrightarrow{AB}}}=-2}$
$\begin{array}{rcl} y_{_{\overrightarrow{AB}}}&=&y_{B}-y_{A}\\\\&=&5-3\\\\&=&2\end{array}$
On trouve alors : $\boxed{y_{_{\overrightarrow{AB}}}=2}$
Ainsi, on obtient :
$$\boxed{\overrightarrow{AB}\begin{pmatrix} -2\\2\end{pmatrix}}$$
c) la distance $AB.$
Soit : $\overrightarrow{AB}\begin{pmatrix} -2\\2\end{pmatrix}.$
Alors, la distance $AB$ est donnée par :
$\begin{array}{rcl} AB&=&\sqrt{(-2)^{2}+(2)^{2}}\\\\&=&\sqrt{4+4}\\\\&=&\sqrt{8}\\\\&=&2\sqrt{2}\end{array}$
Donc, $\boxed{AB=2\sqrt{2}}$
5) $(\Delta)$ est une droite perpendiculaire à $(d).$
Déterminons alors le coefficient directeur de la droite $(\Delta).$
Remarquons tout d'abord que le coefficient directeur de $(d)$ est égal à $2.$
Soit $a$ est le coefficient directeur de $(\Delta).$
Comme $(\Delta)$ est perpendiculaire à $(d)$ alors, les coefficients directeurs de ces deux droites vérifient la condition d'orthogonalité.
Ce qui signifie que : $2\times a=-1$
Ce qui entraine alors : $a=-\dfrac{1}{2}$
Ainsi, le coefficient directeur de $(\Delta)$ est égal à $-\dfrac{1}{2}$
6) $(\Delta)$ est la droite perpendiculaire à $(d)$ qui passe par le point $B.$
Traçons la droite $(\Delta)$ et, sans calcul, donnons une équation de $(\Delta).$
En effet, comme le coefficient directeur de $(\Delta)$ est égal à $-\dfrac{1}{2}$ alors, une équation de $(\Delta)$ est de la forme :
$$y=-\dfrac{1}{2}x+b$$
Comme $(\Delta)$ passe par $B$ alors, l'ordonnée à l'origine $b$ est égale à l'ordonnée de $B.$
Donc, $b=5$
D'où,
$$\boxed{(\Delta)\ :\ y=-\dfrac{1}{2}x+5}$$

Exercice 15
Dans le plan muni d'un repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j})$, on donne :
$\overrightarrow{AO}(2\;;\ -7 )\;,\ \overrightarrow{OB}(-5\;;\ -2)\;,\ C(7\;;\ -2)\ $ et $\ \overrightarrow{DC}(6\;;\ -6 ).$
1) Déterminons les coordonnées des points $A\;,\ B\ $ et $\ D.$
On sait que : $\overrightarrow{OA}=-\overrightarrow{AO}.$
Or, les coordonnées de $-\overrightarrow{OA}$ sont :
$-\overrightarrow{AO}\begin{pmatrix} -2\\-(-7)\end{pmatrix}=\begin{pmatrix} -2\\7\end{pmatrix}$
Donc, $\overrightarrow{OA}\begin{pmatrix} -2\\7\end{pmatrix}$
D'où,
$$\boxed{A\begin{pmatrix} -2\\7\end{pmatrix}}$$
On a : $\overrightarrow{OB}(-5\;;\ -2)$
Alors,
$$\boxed{B\begin{pmatrix} -5\\-2\end{pmatrix}}$$
Soit : $\overrightarrow{DC}(6\;;\ -6 ).$
Comme $\overrightarrow{DC}\begin{pmatrix} x_{C}-x_{D}\\y_{C}-y_{D}\end{pmatrix}$ alors, on a :
$\begin{array}{rcl}\overrightarrow{DC}(6\;;\ -6 )&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{C}-x_{D}&=&6\\\\y_{C}-y_{D}&=&-6\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} 7-x_{D}&=&6\\\\-2-y_{D}&=&-6\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} -x_{D}&=&6-7\\\\-y_{D}&=&-6+2\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} -x_{D}&=&-1\\\\-y_{D}&=&-4\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{D}&=&1\\\\y_{D}&=&4\end{array}\right.\\\\\end{array}$
D'où,
$$\boxed{D\begin{pmatrix} 1\\4\end{pmatrix}}$$
2) Plaçons les points $A\;,\ B\;,\ C\ $ et $\ D.$
3) Montrons que :
a) les points $A\;,\ D\ $ et $\ C$ sont alignés.
Pour cela, on peut montrer que les vecteurs $\overrightarrow{AC}\ $ et $\ \overrightarrow{AD}$ sont colinéaires.
En calculant les cordonnées de ces deux vecteurs, on obtient :
$\overrightarrow{AC}\begin{pmatrix} 7-(-2)\\-2-7\end{pmatrix}=\begin{pmatrix} 9\\-9\end{pmatrix}$
$\overrightarrow{AD}\begin{pmatrix} 1-(-2)\\4-7\end{pmatrix}=\begin{pmatrix} 3\\-3\end{pmatrix}$
On remarque alors qu'en multipliant par $3$ les coordonnées du vecteur $\overrightarrow{AD}$, on trouve celles de $\overrightarrow{AC}.$
Ce qui signifie que : $\overrightarrow{AC}=3\overrightarrow{AD}$
D'où, les vecteurs $\overrightarrow{AC}\ $ et $\ \overrightarrow{AD}$ sont colinéaires.
Par conséquent, les points $A\;,\ D\ $ et $\ C$ sont alignés.
b) le triangle $ABD$ est rectangle en $D.$
Pour cela, calculons d'abord les distances $AB\;;\ AD\ $ et $\ BD.$
Soit : $\overrightarrow{AB}\begin{pmatrix} -5-(-2)\\-2-7\end{pmatrix}=\begin{pmatrix} -3\\-9\end{pmatrix}$ alors, on a :
$\begin{array}{rcl} AB&=&\sqrt{(-3)^{2}+(-9)^{2}}\\\\&=&\sqrt{9+81}\\\\&=&\sqrt{90}\\\\&=&\sqrt{9\times 10}\\\\&=&\sqrt{9}\times\sqrt{10}\\\\&=&3\sqrt{10}\end{array}$
Ainsi, $\boxed{AB=3\sqrt{10}}$
Soit : $\overrightarrow{AD}\begin{pmatrix} 3\\-3\end{pmatrix}$ alors, on a :
$\begin{array}{rcl} AD&=&\sqrt{(3)^{2}+(-3)^{2}}\\\\&=&\sqrt{9+9}\\\\&=&\sqrt{18}\\\\&=&\sqrt{9\times 2}\\\\&=&\sqrt{9}\times\sqrt{2}\\\\&=&3\sqrt{2}\end{array}$
D'où, $\boxed{AD=3\sqrt{2}}$
Soit : $\overrightarrow{BD}\begin{pmatrix} 1-(-5)\\4-(-2)\end{pmatrix}=\begin{pmatrix} 6\\6\end{pmatrix}$ alors, on a :
$\begin{array}{rcl} BD&=&\sqrt{(6)^{2}+(-6)^{2}}\\\\&=&\sqrt{36+36}\\\\&=&\sqrt{72}\\\\&=&\sqrt{36\times 2}\\\\&=&\sqrt{36}\times\sqrt{2}\\\\&=&6\sqrt{2}\end{array}$
Donc, $\boxed{BD=6\sqrt{2}}$
Puis, en mettant au carré ces distance, on trouve :
$AB^{2}=(3\sqrt{10})^{2}=90$
$AD^{2}=(3\sqrt{2})^{2}=18$
$BD^{2}=(6\sqrt{2})^{2}=72$
Alors, on remarque que : $18+72=180$
Ce qui signifie que : $AD^{2}+BD^{2}=AB^{2}.$
Ainsi, d'après la réciproque du théorème de Pythagore $ABD$ est un triangle rectangle en $D.$

Exercice 16
Le plan est muni d'un repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j})$ ; on désigne par $(d)$ la droite passant par $A\left(\dfrac{13}{2}\;;\ 4\right)\ $ et $\ B\left(-\dfrac{5}{2}\;;\ -2\right)\ $ et $\ (d')\ :\ y=-\dfrac{3}{2}x+4$
1) Déterminons une équation de $(d).$
Soit : $y=ax+b$ une équation réduite de la droite $(d)$ avec, $a$ le coefficient directeur et $b$ l'ordonnée à l'origine.
Déterminons alors $a\ $ et $\ b$
En effet, comme $(d)$ passe par les points $A\ $ et $\ B$ alors, $\overrightarrow{AB}$ est un vecteur directeur de $(d).$
Soit alors :
$\overrightarrow{AB}\begin{pmatrix} -\dfrac{5}{2}-\dfrac{13}{2}\\\\-2-4\end{pmatrix}=\begin{pmatrix} -\dfrac{18}{2}\\\\-6\end{pmatrix}=\begin{pmatrix} -9\\-6\end{pmatrix}$
Ainsi, le coefficient directeur $a$ est donné par :
$$a=\dfrac{-6}{-9}=\dfrac{2}{3}$$
Dans l'équation réduite, en remplaçant $a$ par sa valeur $\dfrac{2}{3}$, on obtient :
$$y=\dfrac{2}{3}x+b$$
Par ailleurs, on sait que : $(d)$ passe par le point $B.$
Donc, les coordonnées de ce point vérifient l'équation de $(d).$
C'est-à-dire ; $y_{B}=\dfrac{2}{3}\times x_{B}+b$
Soit alors : $-2=\dfrac{2}{3}\times\left(-\dfrac{5}{2}\right)+b$
Ce qui donne : $-2=-\dfrac{5}{3}+b$
Par suite,
$\begin{array}{rcl} b&=&-2+\dfrac{5}{3}\\\\&=&-\dfrac{6}{3}+\dfrac{5}{3}\\\\&=&-\dfrac{1}{3}\end{array}$
D'où,
$$b=-\dfrac{1}{3}$$
Ainsi, une équation réduite de la droite $(d)$ est donnée par :
$$\boxed{(d)\ :\ y=\dfrac{2}{3}x-\dfrac{1}{3}}$$
Montrons que $(d)\ $ et $\ (d')$ sont perpendiculaires.
Soit $a=\dfrac{3}{2}$ le coefficient directeur de $(d)\ $ et $\ a'=-\dfrac{3}{2}$ le coefficient directeur de $(d').$
Alors, en faisant le produit de ces deux coefficients directeurs, on trouve :
$$a\times a'=\dfrac{2}{3}\times\left(-\dfrac{3}{2}\right)=-1$$
On constate que ce produit est égal à $-1.$
Ce qui signifie que les coefficients directeur des droites $(d)\ $ et $\ (d')$ vérifient la condition d'orthogonalité.
Par conséquent, les droites $(d)\ $ et $\ (d')$ sont perpendiculaires.
Calculons les coordonnées de leur point d'intersection $E.$
En effet, comme $E$ est le point d'intersection de $(d)\ $ et $\ (d')$ alors, ses coordonnées sont solutions du système d'équations formé par les équations respectives des droites $(d)\ $ et $\ (d').$
Soit alors, à résoudre le système suivant :
$$\left\lbrace\begin{array}{rclr}y&=&\dfrac{2}{3}x-\dfrac{1}{3}&\quad(1)\\\\y&=&-\dfrac{3}{2}x+4&\quad(2)\end{array}\right.$$
Par comparaison des équations $(1)\ $ et $\ (2)$, on obtient :
$\begin{array}{rcl} \text{équation }(1)=\text{équation }(2)&\Leftrightarrow&\dfrac{2}{3}x-\dfrac{1}{3}=-\dfrac{3}{2}x+4\\\\&\Leftrightarrow&\dfrac{2}{3}x+\dfrac{3}{2}x=4+\dfrac{1}{3}\\\\&\Leftrightarrow&\dfrac{4}{6}x+\dfrac{9}{6}x=\dfrac{12}{3}+\dfrac{1}{3}\\\\&\Leftrightarrow&\dfrac{13}{6}x=\dfrac{13}{3}\\\\&\Leftrightarrow&x=\dfrac{\dfrac{13}{3}}{\dfrac{13}{6}}\\\\&\Leftrightarrow&x=\dfrac{13}{3}\times\dfrac{6}{13}\\\\&\Leftrightarrow&x=\dfrac{6}{3}\\\\&\Leftrightarrow&x=2\end{array}$
Donc, $\boxed{x=2}$
Ensuite, en remplaçant cette valeur de $x$ dans l'équation $(1)$, on trouve :
$\begin{array}{rcl} y&=&\dfrac{2}{3}\times 2-\dfrac{1}{3}\\\\&=&\dfrac{4}{3}-\dfrac{1}{3}\\\\&=&\dfrac{3}{3}\\\\&=&1\end{array}$
Donc, $\boxed{y=1}$
D'où, $S=\left\lbrace(2\;;\ 1)\right\rbrace$
Ainsi, les coordonnées de $E$ sont données par :
$$\boxed{E\begin{pmatrix} 2\\1\end{pmatrix}}$$
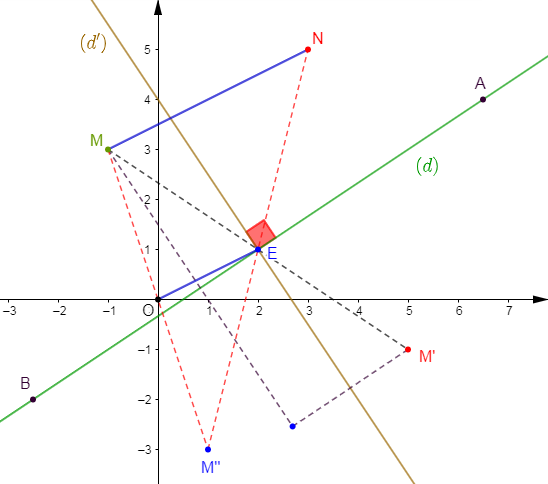
2) soit $M(-1\;;\ 3)$ un point du plan
a) On appelle $M'$ image de $M$ par la symétrie d'axe $(d)$ suivie de la symétrie d'axe $(d')$ ; montrons que $E$ est le milieu de $[MM']$ puis déterminons les coordonnées de $M'.$
En effet, comme $(d)\ $ et $\ (d')$ sont perpendiculaires alors, la symétrie d'axe $(d)$ suivie de la symétrie d'axe $(d')$ est la symétrie centrale de centre $E.$
Donc, $M'=S_{E}(M).$
Ce qui signifie que $M'$ est le symétrique de $M$ par rapport au point $E.$
D'où, $E$ est le milieu de $[MM'].$
Déterminons les coordonnées de $M'.$
Comme $E$ milieu de $[MM']$ alors, $\overrightarrow{EM'}=\overrightarrow{ME}$
Or, on sait que deux vecteurs sont égaux s'ils ont les mêmes coordonnées.
Soit alors :
$\overrightarrow{EM'}\begin{pmatrix} x_{M'}-2\\\\y_{M'}-1\end{pmatrix}$
$\overrightarrow{ME}\begin{pmatrix} 2-(-1)\\1-3\end{pmatrix}=\begin{pmatrix} 3\\-2\end{pmatrix}$
Ainsi, on a :
$\begin{array}{rcl}\overrightarrow{EM'}=\overrightarrow{ME}&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{M'}-2&=&3\\\\y_{M'}-1&=&-2\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{M'}&=&3+2\\\\y_{M'}&=&-2+1\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{M'}&=&5\\\\y_{M'}&=&-1\end{array}\right.\end{array}$
D'où,
$$\boxed{M'\begin{pmatrix} 5\\-1\end{pmatrix}}$$
b) On appelle $N$ image de $M$ dans la symétrie de centre $O$ suivie de la symétrie de centre $E.$
Démontrons que $\overrightarrow{MN}=2\times\overrightarrow{OE}$ puis déterminons les coordonnées de $N.$
Dans la première symétrie centrale de centre $O$, considérons $M''$ comme image de $M.$
Alors, on a : $O$ est milieu de $[MM''].$
Ce qui entraine : $\overrightarrow{MM''}=2\times\overrightarrow{OM''}\qquad(1)$
Dans la première symétrie centrale de centre $E$, on a $N$ image de $M''.$
Donc, $E$ est milieu de $[M''N].$
Ce qui signifie que : $\overrightarrow{M''N}=2\times\overrightarrow{M''E}\qquad(2)$
En additionnant, membre à membre, les relations $(1)\ $ et $\ (2)$, on trouve :
$\overrightarrow{MM''}+\overrightarrow{M''N}=2\times\overrightarrow{OM''}+2\times\overrightarrow{M''E}=2\times\left(\overrightarrow{OM''}+\overrightarrow{M''E}\right)$
Or, d'après la relation de Chasles, on a :
$\overrightarrow{MM''}+\overrightarrow{M''N}=\overrightarrow{MN}\ $ et $\ \overrightarrow{OM''}+\overrightarrow{M''E}=\overrightarrow{OE}$
D'où, $\boxed{\overrightarrow{MN}=2\times\overrightarrow{OE}}$
Déterminons les coordonnées du point $N.$
On a : $\overrightarrow{MN}=2\times\overrightarrow{OE}.$
Or, on sait que deux vecteurs sont égaux s'ils ont les mêmes coordonnées.
Alors, calculons les coordonnées des vecteurs $\overrightarrow{MN}\ $ et $\ 2\times\overrightarrow{OE}$
Soit :
$\overrightarrow{MN}\begin{pmatrix} x_{N}-(-1)\\\\y_{N}-3\end{pmatrix}=\begin{pmatrix} x_{N}+1\\\\y_{N}-3\end{pmatrix}$
$2\times\overrightarrow{OE}\begin{pmatrix} 2\times 2\\2\times 1\end{pmatrix}=\begin{pmatrix} 4\\2\end{pmatrix}$
Ainsi, on a :
$\begin{array}{rcl}\overrightarrow{MN}=2\times\overrightarrow{OE}&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{N}+1&=&4\\\\y_{N}-3&=&2\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{N}&=&4-1\\\\y_{N}&=&2+3\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{N}&=&3\\\\y_{N}&=&5\end{array}\right.\end{array}$
D'où,
$$\boxed{N\begin{pmatrix} 3\\5\end{pmatrix}}$$

Exercice 17
Dans un repère orthonormal on considère les droites $(D)\ :\ 2x-y-3=0\ $ et $\ (D')\ :\ -2x+y+1=0$
1) Représentons $(D)\ $ et $\ (D')$ dans le repère puis, montrons que $(D)\parallel(D')$
$-\ $ représentation de $(D)$
Choisissons deux points $B\ $ et $\ C$ dont les coordonnées vérifient l'équation de $(D).$
On a :
si $x=0$ alors, $-y-3=0\ \Rightarrow\ y=-3$
si $x=1$ alors, $2-y-3=0\ \Rightarrow\ y=-1$
Donc, plaçons les points $B\begin{pmatrix} 0\\-3\end{pmatrix}\ $ et $\ C\begin{pmatrix} 1\\-1\end{pmatrix}$ puis, traçons la droite passant par $B\ $ et $\ C.$ C'est la droite $(D).$
$-\ $ Représentation de $(D')$
De la même manière, choisissons deux points $G\ $ et $\ H$ dont les coordonnées vérifient l'équation de $(D').$
On a :
si $x=0$ alors, $y+1=0\ \Rightarrow\ y=-1$
si $x=1$ alors, $-2+y+1=0\ \Rightarrow\ y=1$
Plaçons alors les points $G\begin{pmatrix} 0\\-1\end{pmatrix}\ $ et $\ H\begin{pmatrix} 1\\1\end{pmatrix}$ puis, traçons la droite passant par $G\ $ et $\ H.$ C'est la droite $(D').$
Montrons que $(D)\ $ et $\ (D')$ sont parallèles.
Soit : $(D)\ :\ 2x-y-3=0$ alors, $\vec{u}\begin{pmatrix} 1\\2\end{pmatrix}$ est un vecteur directeur de $(D).$
Par suite, le coefficient directeur $a$ de la droite $(D)$ est donné par :
$$a=\dfrac{2}{1}=2$$
Soit : $(D')\ :\ -2x+y+1=0$ alors, $\vec{v}\begin{pmatrix} -1\\-2\end{pmatrix}$ est un vecteur directeur de $(D').$
Ainsi, le coefficient directeur $a'$ de la droite $(D')$ est donné par :
$$a'=\dfrac{-2}{-1}=2$$
On remarque alors que ces deux coefficients directeurs sont égaux : $a=a'$
Par conséquent, les droites $(D)\ $ et $\ (D')$ sont parallèles.
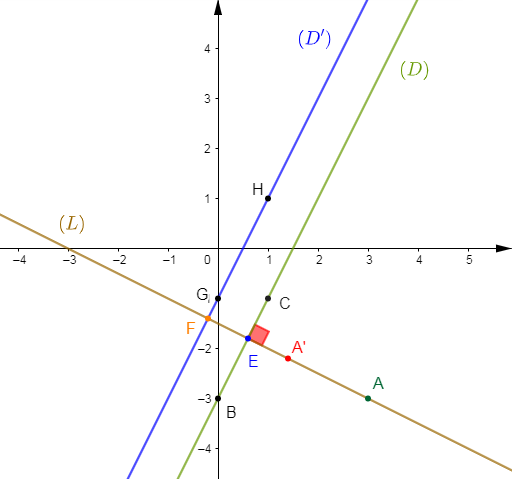
2) Soit $A(3\;;\ -3)$ ; construisons la droite $(L)$ qui est perpendiculaire à $(D)$ et passant par le point $A$ puis, déterminons l'équation de la droite $(L)$ et trouvons les coordonnées des points $E\ $ et $\ F$ intersections respectives de $(D)\ $ et $\ (D')$ avec $(L).$
L'équation de la droite $(L)$ peut se mettre sous la forme :
$$y=a''x+b$$
avec $a''$ son coefficient directeur et $b$ son ordonnée à l'origine.
Déterminons alors $a''\ $ et $\ b.$
Comme $(L)$ est perpendiculaire à $(D)$ alors, les coefficients directeurs de ces deux droites vérifient :
$$a''\times 2=-1\ \Rightarrow\ a''=\dfrac{-1}{2}$$
Par suite, une équation réduite de la droite $(L)$ est de la forme :
$$y=\dfrac{-1}{2}x+b$$
Par ailleurs, la droite $(L)$ passe par $A(3\;;\ -3)$ donc, les coordonnées de ce point vérifient l'équation réduite de $(L).$
Ainsi,
$\begin{array}{rcl} -3=\dfrac{-1}{2}\times 3+b&\Rightarrow&b=-3+\dfrac{3}{2}\\\\&\Rightarrow&b=-\dfrac{6}{2}+\dfrac{3}{2}\\\\&\Rightarrow&b=\dfrac{-6+3}{2}\\\\&\Rightarrow&b=-\dfrac{3}{2}\end{array}$
D'où, une équation réduite de la droite $(L)$ passant par $A(3\;;\ -3)$ et perpendiculaire à la droite $(D)$ est donnée par :
$$\boxed{(L)\ :\ y=-\dfrac{1}{2}x-\dfrac{3}{2}}$$
Trouvons les coordonnées du point $E$ intersection de $(D)$ avec $(L).$
Comme $E$ est le point d'intersection de $(D)\ $ et $\ (L)$ alors, ses coordonnées sont solutions du système d'équations formé par les équations respectives des droites $(D)\ $ et $\ (L).$
Soit alors, à résoudre le système suivant :
$$\left\lbrace\begin{array}{rclr}2x-y-3&=&0&\quad(1)\\\\y&=&-\dfrac{1}{2}x-\dfrac{3}{2}&\quad(2)\end{array}\right.$$
Par substitution, on remplace $y$ dans l'équation $(1)$ par son expression dans l'équation $(2).$
On obtient alors :
$\begin{array}{rcl}2x-\left(-\dfrac{1}{2}x-\dfrac{3}{2}\right)-3=0&\Rightarrow&2x+\dfrac{1}{2}x+\dfrac{3}{2}-3=0\\\\&\Rightarrow&\dfrac{4}{2}x+\dfrac{1}{2}x+\dfrac{3}{2}-\dfrac{6}{2}=0\\\\&\Rightarrow&\dfrac{5}{2}x-\dfrac{3}{2}=0\\\\&\Rightarrow&\dfrac{5}{2}x=\dfrac{3}{2}\\\\&\Rightarrow&x=\dfrac{\dfrac{3}{2}}{\dfrac{5}{2}}\\\\&\Rightarrow&x=\dfrac{3}{2}\times\dfrac{2}{5}\\\\&\Rightarrow&x=\dfrac{3}{5}\end{array}$
Donc, $\boxed{x=\dfrac{3}{5}}$
Ensuite, en remplaçant cette valeur de $x$ dans l'équation $(2)$, on trouve :
$\begin{array}{rcl} y&=&-\dfrac{1}{2}\times\dfrac{3}{5}-\dfrac{3}{2}\\\\&=&-\dfrac{3}{10}-\dfrac{3}{2}\\\\&=&-\dfrac{3}{10}-\dfrac{15}{10}\\\\&=&-\dfrac{18}{10}\\\\&=&-\dfrac{9}{5}\end{array}$
Donc, $\boxed{y=-\dfrac{9}{5}}$
D'où, $S=\left\lbrace\left(\dfrac{3}{5}\;;\ -\dfrac{9}{5}\right)\right\rbrace$
Par conséquent, les coordonnées de $E$ sont données par :
$$\boxed{E\begin{pmatrix} \dfrac{3}{5}\\\\-\dfrac{9}{5}\end{pmatrix}}$$
Trouvons les coordonnées du point $F$ intersection de $(D')$ avec $(L).$
$F$ étant le point d'intersection de $(D')\ $ et $\ (L)$ alors, ses coordonnées sont solutions du système d'équations formé par les équations respectives des droites $(D')\ $ et $\ (L).$
Soit alors, à résoudre le système suivant :
$$\left\lbrace\begin{array}{rclr}-2x+y+1&=&0&\quad(1)\\\\y&=&-\dfrac{1}{2}x-\dfrac{3}{2}&\quad(2)\end{array}\right.$$
Par substitution, on remplace $y$ dans l'équation $(1)$ par son expression dans l'équation $(2).$
On obtient alors :
$\begin{array}{rcl}-2x+\left(-\dfrac{1}{2}x-\dfrac{3}{2}\right)+1=0&\Rightarrow&-2x-\dfrac{1}{2}x-\dfrac{3}{2}+1=0\\\\&\Rightarrow&-\dfrac{4}{2}x-\dfrac{1}{2}x-\dfrac{3}{2}+\dfrac{2}{2}=0\\\\&\Rightarrow&-\dfrac{5}{2}x-\dfrac{1}{2}=0\\\\&\Rightarrow&-\dfrac{5}{2}x=\dfrac{1}{2}\\\\&\Rightarrow&x=\dfrac{\dfrac{1}{2}}{-\dfrac{5}{2}}\\\\&\Rightarrow&x=\dfrac{1}{2}\times\left(-\dfrac{2}{5}\right)\\\\&\Rightarrow&x=-\dfrac{1}{5}\end{array}$
Donc, $\boxed{x=-\dfrac{1}{5}}$
Ensuite, en remplaçant cette valeur de $x$ dans l'équation $(2)$, on trouve :
$\begin{array}{rcl} y&=&-\dfrac{1}{2}\times\left(-\dfrac{1}{5}\right)-\dfrac{3}{2}\\\\&=&\dfrac{1}{10}-\dfrac{3}{2}\\\\&=&\dfrac{1}{10}-\dfrac{15}{10}\\\\&=&-\dfrac{14}{10}\\\\&=&-\dfrac{7}{5}\end{array}$
Donc, $\boxed{y=-\dfrac{7}{5}}$
D'où, $S=\left\lbrace\left(-\dfrac{1}{5}\;;\ -\dfrac{7}{5}\right)\right\rbrace$
Par conséquent, les coordonnées de $F$ sont données par :
$$\boxed{F\begin{pmatrix} -\dfrac{1}{5}\\\\-\dfrac{7}{5}\end{pmatrix}}$$
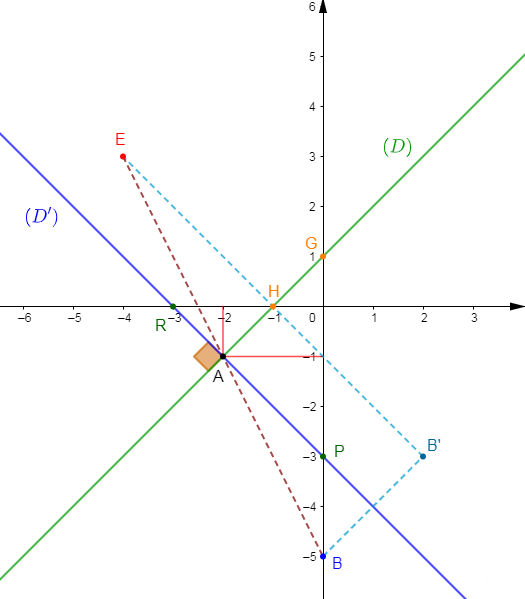
3) Construisons l'image $A'\ $ de $\ A$ par la symétrie orthogonale d'axe $(D)$ suivie de la symétrie orthogonale d'axe $(D').$
Calculons les coordonnées de $A'.$
En effet, on sait que $A$ appartient à $(L)$ et que les droites $(D)\ $ et $\ (L)$ sont perpendiculaires en $E.$
De, d'après le résultat de la question $1)$, on a : $(D)$ parallèle à $(D').$
Or, on sait que si deux droites sont parallèles alors, toute droite perpendiculaire à l'une est aussi perpendiculaire à l'autre.
Ainsi, comme $(L)$ est perpendiculaire à $(D)$ alors, $(L)$ est aussi perpendiculaire à $(D')$
Donc, $(D')\ $ et $\ (L)$ sont perpendiculaires en $F.$
Alors, l'image $A'\ $ de $\ A$ par la symétrie orthogonale d'axe $(D)$ suivie de la symétrie orthogonale d'axe $(D')$ est déterminée par l'image de $A$ par la symétrie centrale de centre $E$ suivie de la symétrie centrale de centre $F.$
Par suite, en utilisant une propriété démontrée à la dernière question de l'exercice précédent, on obtient :
$$\overrightarrow{AA'}=2\times\overrightarrow{EF}$$
Or, on sait que deux vecteurs sont égaux s'ils ont les mêmes coordonnées.
Calculons alors les coordonnées des vecteurs $\overrightarrow{AA'}\ $ et $\ 2\times\overrightarrow{EF}$
Soit :
$\overrightarrow{AA'}\begin{pmatrix} x_{A'}-3\\\\y_{A'}-(-3)\end{pmatrix}=\begin{pmatrix} x_{A'}-3\\\\y_{A'}+3\end{pmatrix}$
$\overrightarrow{EF}\begin{pmatrix} -\dfrac{1}{5}-\dfrac{3}{5} \\\\-\dfrac{7}{5}-\left(-\dfrac{9}{5}\right)\end{pmatrix}=\begin{pmatrix} -\dfrac{4}{5}\\\\-\dfrac{7}{5}+\dfrac{9}{5}\end{pmatrix}=\begin{pmatrix} -\dfrac{4}{5}\\\\\dfrac{2}{5}\end{pmatrix}$
Donc, $2\times\overrightarrow{EF}\begin{pmatrix} 2\times\left(-\dfrac{4}{5}\right)\\\\2\times\dfrac{2}{5}\end{pmatrix}=\begin{pmatrix} -\dfrac{8}{5}\\\\\dfrac{4}{5}\end{pmatrix}$
Ainsi, on a :
$\begin{array}{rcl}\overrightarrow{AA'}=2\times\overrightarrow{EF}&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{A'}-3&=&-\dfrac{8}{5}\\\\y_{A'}+3&=&\dfrac{4}{5}\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{A'}&=&-\dfrac{8}{5}+3\\\\y_{A'}&=&\dfrac{4}{5}-3\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{A'}&=&-\dfrac{8}{5}+\dfrac{15}{5}\\\\y_{A'}&=&\dfrac{4}{5}-\dfrac{15}{5}\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{A'}&=&\dfrac{7}{5}\\\\y_{A'}&=&-\dfrac{11}{5}\end{array}\right.\end{array}$
D'où,
$$\boxed{A'\begin{pmatrix} \dfrac{7}{5}\\\\-\dfrac{11}{5}\end{pmatrix}}$$

Exercice 18
Le plan est muni d'un R.O.N $(O\;;\ \vec{i}\;,\ \vec{j}).$
Soit $(D)$ la droite d'équation définie par :
$$(\mathcal{D})\ :\ -2x+3y-1=0$$
1) Parmi les points : $A(2\;;\ -1)\;\ B(1\;;\ 1)\;,\ C\left(-\dfrac{1}{2}\;;\ 0\right)\ $ et $\ D(2\;;\ 0)$ indiquons ceux qui appartiennent à $(D).$
On sait que un point appartient à une droite si ses coordonnées vérifient l'équation de cette droite.
Donc, pour chacun de ces points, regardons si ses coordonnées vérifient l'équation de $(\mathcal{D}).$
$-\ $ pour le point $A$, on a :
$\begin{array}{rcl}-2\times x_{A}+3\times y_{A}-1&=&-2\times 2+3\times(-1)-1\\\\&=&-4-3-1\\\\&=&-8\end{array}$
Donc, $\boxed{-2x_{A}+3y_{A}-1\neq 0}$
Ce qui signifie que les coordonnées de $A$ ne vérifient pas l'équation de $(\mathcal{D}).$
D'où, le point $A$ n'appartient pas à la droite $(\mathcal{D}).$
$-\ $ pour le point $B$, on a :
$\begin{array}{rcl}-2\times x_{B}+3\times y_{B}-1&=&-2\times 1+3\times 1-1\\\\&=&-2+3-1\\\\&=&0\end{array}$
Donc, $\boxed{-2x_{B}+3y_{B}-1=0}$
Ce qui signifie que les coordonnées de $B$ vérifient bien l'équation de $(\mathcal{D}).$
Par conséquent, le point $B$ appartient à la droite $(\mathcal{D}).$
$-\ $ pour le point $C$, on a :
$\begin{array}{rcl}-2\times x_{C}+3\times y_{C}-1&=&-2\times\left(-\dfrac{1}{2}\right)+3\times 0-1\\\\&=&\dfrac{2}{2}+0-1\\\\&=&1-1\\\\&=&0\end{array}$
Donc, $\boxed{-2x_{C}+3y_{C}-1=0}$
Ce qui signifie que les coordonnées de $C$ vérifient bien l'équation de $(\mathcal{D}).$
D'où, le point $C$ est sur la droite $(\mathcal{D}).$
$-\ $ pour le point $D$, on a :
$\begin{array}{rcl}-2\times x_{D}+3\times y_{D}-1&=&-2\times 2+3\times 0-1\\\\&=&-4+0-1\\\\&=&-5\end{array}$
Donc, $\boxed{-2x_{D}+3y_{D}-1\neq 0}$
Ce qui signifie que les coordonnées de $D$ ne vérifient pas l'équation de $(\mathcal{D}).$
Par conséquent, le point $D$ n'appartient pas à la droite $(\mathcal{D}).$
2) Déterminons une équation réduite de la droite $(\mathcal{D}).$
Une équation réduite de $(\mathcal{D})$ est de la forme :
$$y=ax+b$$
Donc, en partant de l'équation générale de $(\mathcal{D})$, nous allons exprimer $y$ en fonction de $x.$ C'est-à-dire ; réécrire l'équation sous forme : $y=ax+b.$
On a :
$\begin{array}{rcl}-2x+3y-1=0&\Leftrightarrow&3y=2x+1\\\\&\Leftrightarrow&y=\dfrac{2x+1}{3}\\\\&\Leftrightarrow&y=\dfrac{2x}{3}+\dfrac{1}{3}\\\\&\Leftrightarrow&y=\dfrac{2}{3}x+\dfrac{1}{3}\end{array}$
D'où, une équation réduite de la droite $(\mathcal{D})$ est donnée par :
$$\boxed{(\mathcal{D})\ :\ y=\dfrac{2}{3}x+\dfrac{1}{3}}$$
3) Déterminons le coefficient directeur ; l'ordonnée à l'origine et un vecteur directeur de la droite $(\mathcal{D}).$
En effet, on sait que si une droite est d'équation $y=ax+b$ alors, son coefficient directeur est égal à $a$, son ordonnée à l'origine est égale à $b$ et le vecteur $\vec{u}\begin{pmatrix}1\\a\end{pmatrix}$ est un vecteur directeur de cette droite.
Donc, dans cette question, comme $(\mathcal{D})$ est d'équation $y=\dfrac{2}{3}x+\dfrac{1}{3}$ alors, on a :
$\dfrac{2}{3}$ est le coefficient directeur de $(\mathcal{D})$
$\dfrac{1}{3}$ est l'ordonnée à l'origine de la droite $(\mathcal{D})$
$\vec{u}\begin{pmatrix}1\\\\\dfrac{2}{3}\end{pmatrix}$ est un vecteur directeur de la droite $(\mathcal{D})$

Exercice 19
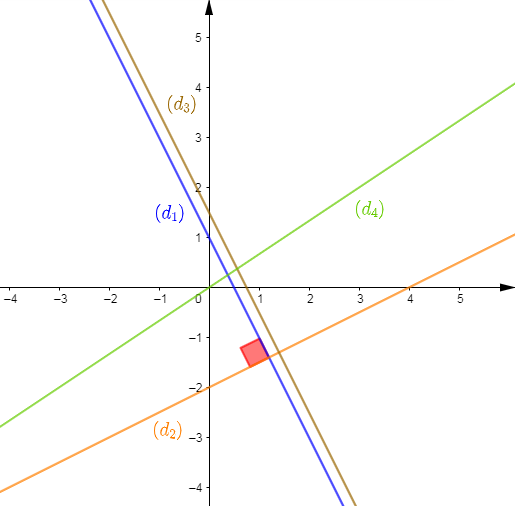
On considère les équations des droites suivantes :
$(d_{1})\ :\ 2x+y-1=0\;,\quad (d_{2})\ :\ -x+2y+4=0$
$(d_{3})\ :\ 4x+2y-3=0\;,\quad (d_{4})\ :\ 2x-3y=0.$
1) Mettons toutes ces équations sous la forme réduite.
En effet, on sait que la forme réduite d'une équation de droite est donnée par :
$$y=ax+b$$
avec $a$ son coefficient directeur et $b$ son ordonnée à l'origine.
Donc, pour chacune de ces équations, nous allons exprimer $y$ en fonction de $x.$
$-\ $ pour la droite $(d_{1})$, on a :
$\begin{array}{rcl}2x+y-1=0&\Leftrightarrow&y=-2x+1\end{array}$
D'où, une équation réduite de la droite $(d_{1})$ est donnée par :
$$\boxed{(d_{1})\ :\ y=-2x+1}$$
$-\ $ pour la droite $(d_{2})$, on a :
$\begin{array}{rcl}-x+2y+4=0&\Leftrightarrow&2y=x-4\\\\&\Leftrightarrow&y=\dfrac{x-4}{2}\\\\&\Leftrightarrow&y=\dfrac{x}{2}-\dfrac{4}{2}\\\\&\Leftrightarrow&y=\dfrac{1}{2}x-2\end{array}$
Ainsi, une équation réduite de la droite $(d_{2})$ est donnée par :
$$\boxed{(d_{2})\ :\ y=\dfrac{1}{2}x-2}$$
$-\ $ pour la droite $(d_{3})$, on a :
$\begin{array}{rcl}4x+2y-3=0&\Leftrightarrow&2y=-4x+3\\\\&\Leftrightarrow&y=\dfrac{-4x+3}{2}\\\\&\Leftrightarrow&y=\dfrac{-4x}{2}+\dfrac{3}{2}\\\\&\Leftrightarrow&y=-2x+\dfrac{3}{2}\end{array}$
Alors, une équation réduite de la droite $(d_{3})$ est donnée par :
$$\boxed{(d_{3})\ :\ y=-2x+\dfrac{3}{2}}$$
$-\ $ pour la droite $(d_{4})$, on a :
$\begin{array}{rcl}2x-3y=0&\Leftrightarrow&-3y=-2x\\\\&\Leftrightarrow&y=\dfrac{-2x}{-3}\\\\&\Leftrightarrow&y=\dfrac{2}{3}x\end{array}$
Donc, une équation réduite de la droite $(d_{4})$ est donnée par :
$$\boxed{(d_{4})\ :\ y=\dfrac{2}{3}x}$$
2) Déterminons les positions relatives des droites : $(d_{1})\ $ et $\ (d_{2})\;,\ (d_{3})\ $ et $\ (d_{4})\;,\ (d_{3})\ $ et $\ (d_{1}).$
$-\ $ position relative des droites $(d_{1})\ $ et $\ (d_{2})$
D'après le résultat de la question $1)$, on a :
$(d_{1})\ :\ y=-2x+1\ $ et $\ (d_{2})\ :\ y=\dfrac{1}{2}x-2$
Donc, en faisant le produit de leur coefficient directeur, on trouve :
$$-2\times\dfrac{1}{2}=\dfrac{-2}{2}=-1$$
On constate alors que les coefficients directeurs des droites $(d_{1})\ $ et $\ (d_{2})$ vérifient la condition d'orthogonalité.
Par conséquent, les droites $(d_{1})\ $ et $\ (d_{2})$ sont perpendiculaires.
$-\ $ position relative des droites $(d_{3})\ $ et $\ (d_{4})$
D'après le résultat de la question $1)$, on a :
$(d_{3})\ :\ y=-2x+\dfrac{3}{2}\ $ et $\ (d_{4})\ :\ y=\dfrac{2}{3}x$
On constate tout d'abord que ces deux droites n'ont pas le même coefficient directeur. Ce qui signifie qu'elles ne sont pas parallèles.
Alors, faisons le produit des coefficients directeurs.
On trouve :
$$-2\times\dfrac{2}{3}=-\dfrac{4}{3}$$
On remarque que ce produit n'est pas égal à $-1.$
Ce qui signifie que la condition d'orthogonalité n'est pas vérifiée.
Donc, ces deux droites ne sont pas perpendiculaires.
Et par conséquent, les droites $(d_{3})\ $ et $\ (d_{4})$ sont sécantes.
$-\ $ position relative des droites $(d_{3})\ $ et $\ (d_{1})$
On remarque que ces deux droites ont le même coefficient directeur.
Par conséquent, elles sont parallèles.

Exercice 20 BFEM 2008 1er groupe
Dans le plan muni d'un repère orthonormé $(O\;;\ \overrightarrow{OI}\;,\ \overrightarrow{OJ})$, on donne les droites $(D)\ $ et $\ (D')$ telles que :
$(D)\ :\ x-y+1=0\ $ et $\ (D')\ :\ x+y+3=0.$
1) Montrons que les droites $(D)\ $ et $\ (D')$ sont perpendiculaires.
En effet, les droites $(D)\ $ et $\ (D')$ sont perpendiculaires si, et seulement si, la condition d'orthogonalité est vérifiée.
Soit : $\vec{u}\ $ et $\ \vec{v}$ les vecteurs directeurs respectifs des droites $(D)\ $ et $\ (D').$
On a : $\vec{u}\begin{pmatrix} 1\\1\end{pmatrix}\ $ et $\ \vec{v}\begin{pmatrix} -1\\1\end{pmatrix}$
Alors, en vérifiant la condition d'orthogonalité, on obtient :
$\begin{array}{rcl} (x_{_{\vec{u}}}\times x_{_{\vec{v}}})+(y_{_{\vec{u}}}\times y_{_{\vec{v}}})&=&(1\times(-1))+(1\times 1)\\\\&=&-1+1\\\\&=&0\end{array}$
Donc, $\boxed{(x_{_{\vec{u}}}\times x_{_{\vec{v}}})+(y_{_{\vec{u}}}\times y_{_{\vec{v}}})=0}$
Ce qui signifie que les coordonnées des vecteurs directeurs $\vec{u}\ $ et $\ \vec{v}$ vérifient la condition d'orthogonalité.
D'où, $\vec{u}\ $ et $\ \vec{v}$ sont orthogonaux.
Par conséquent, les droites $(D)\ $ et $\ (D')$ sont perpendiculaires.
2) Traçons les droites $(D)\ $ et $\ (D')$ dans le repère.
$-\ $ construction de $(D)$
Choisissons deux points $G\ $ et $\ H$ dont les coordonnées vérifient l'équation de $(D).$
On a :
si $x=0$ alors, $-y+1=0\ \Rightarrow\ y=1$
si $x=-1$ alors, $-1-y+1=0\ \Rightarrow\ y=0$
Donc, plaçons les points $G\begin{pmatrix} 0\\1\end{pmatrix}\ $ et $\ H\begin{pmatrix} -1\\0\end{pmatrix}$ puis, traçons la droite passant par $G\ $ et $\ H.$ C'est la droite $(D).$
$-\ $ construction de $(D')$
De la même manière, choisissons deux points $P\ $ et $\ R$ dont les coordonnées vérifient l'équation de la droite $(D').$
On a :
si $x=0$ alors, $y+3=0\ \Rightarrow\ y=-3$
si $x=-3$ alors, $-3+y+3=0\ \Rightarrow\ y=0$
Donc, plaçons les points $P\begin{pmatrix} 0\\-3\end{pmatrix}\ $ et $\ R\begin{pmatrix} -3\\0\end{pmatrix}$ puis, traçons la droite passant par $P\ $ et $\ R.$ C'est la droite $(D').$
3) Déterminons graphiquement les coordonnées du point d'intersection $A$ de $(D)\ $ et $\ (D').$
On place d'abord le point $A$ qui est le point de rencontre des droites $(D)\ $ et $\ (D').$
Puis, à partir de $A$, on trace une ligne verticale qui coupe l'axe des abscisses au point $-2.$ C'est alors l'abscisse du point $A.$
Ensuite, à partir de $A$, on trace une ligne horizontale. Cette ligne coupe l'axe des ordonnées au point $-1.$ Cette valeur représente alors l'ordonnée du point $A.$
Ainsi, les coordonnées de $A$ sont données par :
$$\boxed{A\begin{pmatrix} -2\\-1\end{pmatrix}}$$
4) Soit $B(0\;;\ -5).$ Construisons le point $E$ image de $B$ par la symétrie orthogonale d'axe $(D')$ suivie de celle d'axe $(D).$
Pour cela, on construit d'abord le point $B'$ image de $B$ par la symétrie orthogonale d'axe $(D')$ puis, on construit le point $E$ image de $B'$ par la symétrie orthogonale d'axe $(D).$
Cette transformation du plan est la symétrie centrale de centre $A.$
En effet, comme les droites $(D)\ $ et $\ (D')$ sont perpendiculaires au point $A$ alors, la symétrie orthogonale d'axe $(D')$ suivie de celle d'axe $(D)$ est la symétrie centrale de centre $A.$
5) Trouvons les coordonnées de $E.$
D'après la question $4)$, on sait que cette transformation du plan est la symétrie centrale de centre $A.$
Donc, $E$ est l'image de $B$ par la symétrie centrale de centre $A.$
Ce qui signifie que $A$ est milieu de $[BE].$
Par suite, $\overrightarrow{AE}=\overrightarrow{BA}$
Or, on sait que deux vecteurs sont égaux s'ils ont les mêmes coordonnées.
Calculons alors les coordonnées des vecteurs $\overrightarrow{AE}\ $ et $\ \overrightarrow{BA}$
Soit :
$\overrightarrow{AE}\begin{pmatrix} x_{E}-(-2)\\\\y_{E}-(-1)\end{pmatrix}=\begin{pmatrix} x_{E}+2\\\\y_{E}+1\end{pmatrix}$
$\overrightarrow{BA}\begin{pmatrix} -2-0\\-1-(-5)\end{pmatrix}=\begin{pmatrix} -2\\4\end{pmatrix}$
Ainsi, on a :
$\begin{array}{rcl}\overrightarrow{AE}=\overrightarrow{BA}&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{E}+2&=&-2\\\\y_{E}+1&=&4\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{E}&=&-2-2\\\\y_{E}&=&4-1\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{E}&=&-4\\\\y_{E}&=&3\end{array}\right.\end{array}$
D'où,
$$\boxed{E\begin{pmatrix} -4\\3\end{pmatrix}}$$

Exercice 21
Dans le plan muni d'un repère orthonormé. On donne les points :
$A(3\;;\ -2)\;,\ B(6\;;\ 4)\ $ et $\ C(-5\;;\ 2).$
1) Déterminons une équation de la droite $(AB)$ puis en déduisons son équation réduite.
En effet, la droite $(AB)$ est la droite passant par les points $A(3\;;\ -2)\ $ et $\ B(6\;;\ 4).$
Soit : $M\begin{pmatrix} x\\y\end{pmatrix}\in(AB)$ alors, $\overrightarrow{AM}\ $ et $\ \overrightarrow{AB}$ sont colinéaires.
On a : $\overrightarrow{AM}\begin{pmatrix} x-3\\y-(-2)\end{pmatrix}=\begin{pmatrix} x-3\\y+2\end{pmatrix}\ $ et $\ \overrightarrow{AB}\begin{pmatrix} 6-3\\4-(-2)\end{pmatrix}=\begin{pmatrix} 3\\6\end{pmatrix}$
Ainsi, en appliquant la condition de colinéarité, on obtient :
$\begin{array}{rcl}\overrightarrow{AM}\ \text{ et }\ \overrightarrow{AB}\ \text{ sont colinéaires}&\Leftrightarrow&(x_{_{\overrightarrow{AM}}}\times y_{_{\overrightarrow{AB}}})-(x_{_{\overrightarrow{AB}}}\times y_{_{\overrightarrow{AM}}})=0\\\\&\Leftrightarrow&[(x-3)\times 6]-[3\times(y+2)]=0\\\\&\Leftrightarrow&6x-18-3y-6=0\\\\&\Leftrightarrow&6x-3y-24=0\end{array}$
D'où, une équation générale de la droite $(AB)$ est donnée par :
$$\boxed{(AB)\ :\ 6x-3y-24=0}$$
En déduisons son équation réduite.
On sait que une équation réduite de la droite $(AB)$ est une équation de la forme :
$$y=ax+b$$
avec $a$ son coefficient directeur et $b$ son ordonnée à l'origine.
Donc, en partant de l'équation générale de $(AB)$, nous allons exprimer $y$ en fonction de $x.$ C'est-à-dire ; réécrire l'équation sous la forme : $y=ax+b.$
Ainsi, comme $(AB)$ est d'équation $6x-3y-24=0$ alors, on a :
$\begin{array}{rcl}6x-3y-24=0&\Leftrightarrow&-3y=-6x+24\\\\&\Leftrightarrow&y=\dfrac{-6x+24}{-3}\\\\&\Leftrightarrow&y=\dfrac{-6x}{-3}+\dfrac{24}{-3}\\\\&\Leftrightarrow&y=2x-8\end{array}$
Ainsi, une équation réduite de la droite $(AB)$ est donnée par :
$$\boxed{(AB)\ :\ y=2x-8}$$
2) Soit $(\mathcal{C})$ le cercle circonscrit au triangle $ABC$ rectangle en $A.$
En effet, comme le triangle $ABC$ est rectangle en $A$ alors, le cercle circonscrit à ce triangle a pour centre le point $I$ ; milieu de l'hypoténuse $[BC].$
En calculant les coordonnées de $I$, on trouve :
$\begin{array}{rcl} x_{I}&=&\dfrac{x_{B}+x_{C}}{2}\\\\&=&\dfrac{6-5}{2}\\\\&=&\dfrac{1}{2}\end{array}$
Donc, $\boxed{x_{I}=\dfrac{1}{2}}$
$\begin{array}{rcl} y_{I}&=&\dfrac{y_{B}+y_{C}}{2}\\\\&=&\dfrac{4+2}{2}\\\\&=&\dfrac{6}{2}\\\\&=&3\end{array}$
Donc, $\boxed{y_{I}=3}$
D'où,
$$\boxed{I\begin{pmatrix} \dfrac{1}{2}\\\\3\end{pmatrix}}$$
a) La droite $(AB)$ coupe l'axe des abscisses en $E.$ Déterminons les coordonnées de $E.$
Comme $(AB)$ coupe l'axe des abscisses en $E$ alors, $E$ appartient à l'axe des abscisses.
D'où, son ordonnée est égale à $0.$ C'est-à-dire ; $\boxed{y_{E}=0}$
Ainsi, en remplaçant, $y$ par $0$, dans l'équation générale de $(AB)$, on trouve l'abscisse de $E.$
On a :
$\begin{array}{rcl}6x-3\times 0-24=0&\Leftrightarrow&6x-0-24=0\\\\&\Leftrightarrow&6x=24\\\\&\Leftrightarrow&x=\dfrac{24}{6}\\\\&\Leftrightarrow&x=4\end{array}$
Donc, $\boxed{x_{E}=4}$
D'où,
$$\boxed{E\begin{pmatrix} 4\\0\end{pmatrix}}$$
b) La droite $(AB)$ coupe l'axe des ordonnées en $F.$ Déterminons les coordonnées de $F.$
Comme $(AB)$ coupe l'axe des ordonnées en $F$ alors, le point $E$ appartient à l'axe des ordonnées.
D'où, son abscisse est égale à $0.$ C'est-à-dire ; $\boxed{x_{F}=0}$
Ainsi, en remplaçant, $x$ par $0$, dans l'équation réduite de $(AB)$, on trouve l'ordonnée de $F.$
On a :
$\begin{array}{rcl} y&=&2\times 0-8\\\\&=&-8\end{array}$
Donc, $\boxed{y_{F}=-8}$
D'où,
$$\boxed{F\begin{pmatrix} 0\\-8\end{pmatrix}}$$
3) Traçons la tangente $(T)$ au cercle $(\mathcal{C})$ en $A$ puis, déterminons une équation de la droite $(T).$
En effet, la tangente $(T)$ au cercle $(\mathcal{C})$ en $A$ est la droite passant par le point $A$ et perpendiculaire au rayon $[IA].$
Donc, si un point $M\begin{pmatrix} x\\y\end{pmatrix}$ appartient à la droite $(T)$ alors, les vecteurs $\overrightarrow{IA}\ $ et $\ \overrightarrow{AM}$ sont orthogonaux.
Calculons alors les coordonnées des vecteurs $\overrightarrow{IA}\ $ et $\ \overrightarrow{AM}.$
On a :
$\overrightarrow{IA}\begin{pmatrix} 3-\dfrac{1}{2}\\\\-2-3\end{pmatrix}=\begin{pmatrix} \dfrac{6}{2}-\dfrac{1}{2}\\\\-5\end{pmatrix}=\begin{pmatrix} \dfrac{5}{2}\\\\-5\end{pmatrix}$
$\overrightarrow{AM}\begin{pmatrix} x-3\\y-(-2)\end{pmatrix}=\begin{pmatrix} x-3\\y+2\end{pmatrix}$
Ainsi, en appliquant la condition d'orthogonalité, on obtient :
$\begin{array}{rcl}\overrightarrow{IA}\ \text{ et }\ \overrightarrow{AM}\ \text{ sont orthogonaux}&\Leftrightarrow&(x_{_{\overrightarrow{IA}}}\times x_{_{\overrightarrow{AM}}})+(y_{_{\overrightarrow{IA}}}\times y_{_{\overrightarrow{AM}}})=0\\\\&\Leftrightarrow&\left[\dfrac{5}{2}\times(x-3)\right]+[(-5)\times(y+2)]=0\\\\&\Leftrightarrow&\dfrac{5}{2}x-\dfrac{15}{2}-5y-10=0\\\\&\Leftrightarrow&\dfrac{5}{2}x-5y-\dfrac{15}{2}-\dfrac{20}{2}=0\\\\&\Leftrightarrow&\dfrac{5}{2}x-5y-\dfrac{35}{2}=0\end{array}$
D'où, une équation de la droite $(T)$ est donnée par :
$$\boxed{(T)\ :\ \dfrac{5}{2}x-5y-\dfrac{35}{2}=0}$$

Exercice 22 BFEM 2009 2e groupe
Le plan est muni d'un R.O.N. $(D)\ :\ y=-2x+1\ $ et $\ (D')\ :\ y+x=0.$
1) Montrons que $(D)\ $ et $\ (D')$ sont sécantes.
En mettant l'équation de $(D')$ sous sa forme réduite, on obtient : $(D')\ :\ y=-x.$
On constate alors que ces deux droites n'ont pas le même coefficient directeur. Ce qui signifie qu'elles ne sont pas parallèles.
De plus, en faisant le produit des coefficients directeurs.
On trouve :
$$-2\times(-1)=2$$
On remarque que ce produit n'est pas égal à $-1.$
Ce qui signifie que la condition d'orthogonalité n'est pas vérifiée.
Donc, ces deux droites ne sont pas perpendiculaires.
Et par conséquent, les droites $(D)\ $ et $\ (D')$ sont sécantes.
2) Traçons les droites $(D)\ $ et $\ (D').$
$-\ $ construction de $(D)$
Choisissons deux points $A\ $ et $\ B$ dont les coordonnées vérifient l'équation de $(D).$
On a :
si $x=0$ alors, $y=1$
si $x=2$ alors, $y=-2\times 2+1=-4+1=-3$
Donc, plaçons les points $A\begin{pmatrix} 0\\1\end{pmatrix}\ $ et $\ B\begin{pmatrix} 2\\-3\end{pmatrix}$ puis, traçons la droite passant par $A\ $ et $\ B.$ C'est la droite $(D).$
$-\ $ construction de $(D')$
On sait que $y=-x$ est une application linéaire donc, la droite $(D')$ passe par le point $O$ et par un point $C$ dont les coordonnées vérifient l'équation de la droite $(D').$
Choisissons alors le point $C.$
On a :
si $x=2$ alors, $y=-2$
Donc, plaçons le point $C\begin{pmatrix} 2\\-2\end{pmatrix}$ puis, traçons la droite passant par $O\ $ et $\ C.$ C'est la droite $(D').$
3) Déterminons le point d'intersection de $(D)\ $ et $\ (D')$
Soit $E$ le point d'intersection des droites $(D)\ $ et $\ (D').$
Donc, ses coordonnées sont solutions du système d'équations formé par les équations respectives des droites $(D')\ $ et $\ (L).$
Soit alors, à résoudre le système suivant :
$$\left\lbrace\begin{array}{rclr}y&=&-2x+1&\quad(1)\\\\y+x&=&0&\quad(2)\end{array}\right.$$
Par substitution, on remplace $y$ dans l'équation $(2)$ par son expression dans l'équation $(1).$
On obtient alors :
$\begin{array}{rcl}-2x+1+x=0&\Rightarrow&-x+1=0\\\\&\Rightarrow&-x=-1\\\\&\Rightarrow&x=1\end{array}$
Donc, $\boxed{x=1}$
Ensuite, en remplaçant cette valeur de $x$ dans l'équation $(1)$, on trouve :
$\begin{array}{rcl} y&=&-2\times 1+1\\\\&=&-2+1\\\\&=&-1\end{array}$
Donc, $\boxed{y=-1}$
D'où, $S=\left\lbrace\left(1\;;\ -1\right)\right\rbrace$
Par conséquent, les coordonnées de $E$ sont données par :
$$\boxed{E\begin{pmatrix} 1\\-1\end{pmatrix}}$$

Exercice 23 BFEM 2ND groupe
Répondons par vrai on faux en justifiant la réponse
1) Soit $M(-2\;;\ -1)\ $ et $\ N(1\;;\ 2)$ dans un repère orthonormal $(O\;,\ \vec{i}\;,\ \vec{j}).$ La médiatrice de $[MN]$ passe par l'origine.$\qquad\text{vrai}$
En effet, on sait que si un point est équidistant des deux extrémités d'un segment alors, il appartient à la médiatrice de ce segment.
Donc, vérifions si $O$ est équidistant des deux extrémités $M\ $ et $\ N$ du segment $[MN].$
C'est-à-dire ; $OM=ON$
On a :
$\begin{array}{rcl}OM&=&\sqrt{(-2)^{2}+(-1)^{2}}\\\\&=&\sqrt{4+1}\\\\&=&\sqrt{5}\end{array}$
Donc, $\boxed{OM=\sqrt{5}}$
$\begin{array}{rcl}ON&=&\sqrt{(1)^{2}+(2)^{2}}\\\\&=&\sqrt{1+4}\\\\&=&\sqrt{5}\end{array}$
Donc, $\boxed{ON=\sqrt{5}}$
On remarque alors que $OM=ON.$
Ce qui signifie que $O$ appartient médiatrice de $[MN].$
2) Les droites d'équations respectives dans un repère orthonormé : $y=\dfrac{7}{2}x\ $ et $\ x=\dfrac{-4}{6}y$ sont perpendiculaires.$\qquad\text{faux}$
En réécrivant l'équation $x=\dfrac{-4}{6}y$ sous sa forme réduite, on obtient :
$y=\dfrac{6}{-4}x=-\dfrac{3}{2}x$
Ainsi, en faisant le produit des coefficients directeurs de ces deux droites, on trouve :
$$-\dfrac{3}{2}\times\dfrac{7}{2}=-\dfrac{21}{4}$$
On remarque alors que ce produit est n'est pas égal à $-1.$
Ce qui signifie que la condition d'orthogonalité n'est pas vérifiée.
Par conséquent, les droites d'équations respectives : $y=\dfrac{7}{2}x\ $ et $\ x=\dfrac{-4}{6}y$ ne sont pas perpendiculaires.
3) Le plan est muni d'un R.O.N : la droite $(d)$ passant par $A(2\;;\ 1)$ et de vecteur $\vec{u}(3\;;\ -1)$ passe par le point $B(2\;;\ 2).\qquad\text{faux}$
En effet, si $(d)$ passe aussi par $B$ alors, les vecteurs $\overrightarrow{AB}\ $ et $\ \vec{u}$ sont colinéaires.
On a : $\overrightarrow{AB}\begin{pmatrix} 2-2\\2-1\end{pmatrix}=\begin{pmatrix} 0\\1\end{pmatrix}$
Alors, en utilisant la condition de colinéarité, on obtient :
$\begin{array}{rcl}(x_{_{\overrightarrow{AB}}}\times y_{_{\vec{u}}})-(x_{_{\vec{u}}}\times y_{_{\overrightarrow{AB}}})&=&(0\times(-1))-(3\times 1)\\\\&=&0-3\\\\&=&-3\end{array}$
Donc, $\boxed{(x_{_{\overrightarrow{AB}}}\times y_{_{\vec{u}}})-(x_{_{\vec{u}}}\times y_{_{\overrightarrow{AB}}})\neq 0}$
Ce qui signifie que la condition de colinéarité n'est pas vérifiée.
Ainsi, les vecteurs $\overrightarrow{AB}\ $ et $\ \vec{u}$ ne sont pas colinéaires.
Par conséquent, la droite $(d)$ ne passe pas par le point $B(2\;;\ 2).$
4) Dans un R.O.N si $A(1\;;\ 1)\ $ et $\ B(1\;;\ 0)$ alors, la droite $(AB)$ a pour équation : $x=1.\qquad\text{vrai}$
Une équation générale de la droite $(AB)$ est donnée par :
$$ax+by+c=0$$
Soit : $\overrightarrow{AB}\begin{pmatrix} 1-1\\0-1\end{pmatrix}=\begin{pmatrix} 0\\-1\end{pmatrix}$ un vecteur directeur de $(AB).$
Alors, on a : $-b=0\ $ et $\ a=-1$
En remplaçant dans l'équation générale, on trouve :
$$-x+c=0$$
Comme la droite $(AB)$ passe par le point $B$ alors, remplaçons ses coordonnées dans cette dernière équation.
On obtient : $-1+c=0\ \Rightarrow\ c=1$
Ainsi, la droite $(AB)$ a pour équation :
$$\boxed{(AB)\ :\ -x+1=0\ \text{ ou encore }\ x=1}$$
5) Le coefficient directeur de la droite $(D)\ :\ -5x+y+3=0$ est $-5.\qquad\text{faux}$
En effet, la forme réduite de l'équation de $(D)$ est donnée par :
$$y=5x-3$$
D'où, le coefficient directeur de la droite $(D)$ est égal à $5$
Exercice 24
$x\ $ et $\ y$ étant des réels.
On donne les vecteurs : $\vec{u}(-5\;;\ x+3)\;;\ \vec{v}(4\;;\ 1-x)\;;\ \vec{w}(2\;;\ -1)\ $ et $\ \vec{z}\left(y\;;\ \dfrac{1}{4}\right)$
1) Déterminons $x$ pour que $\vec{u}\ $ et $\ \vec{v}$ soient colinéaires.
Soit : $\vec{u}(-5\;;\ x+3)\ $ et $\ \vec{v}(4\;;\ 1-x).$
Alors, en appliquant la condition de colinéarité, on obtient :
$\begin{array}{rcl}\vec{u}\ \text{ et }\ \vec{v}\ \text{ sont colinéaires}&\Leftrightarrow&[(-5)\times(1-x)]-[4\times(x+3)]=0\\\\&\Leftrightarrow&-5+5x-4x-12=0\\\\&\Leftrightarrow&x-17=0\\\\&\Leftrightarrow&x=17\end{array}$
D'où, $\boxed{x=17}$
2) Déterminons $y$ pour que $\vec{w}\ $ et $\ \vec{z}$ soient orthogonaux.
Soit : $\vec{w}(2\;;\ -1)\ $ et $\ \vec{z}\left(y\;;\ \dfrac{1}{4}\right).$
Alors, en appliquant la condition de d'orthogonalité, on obtient :
$\begin{array}{rcl}\vec{w}\ \text{ et }\ \vec{z}\ \text{ sont orthogonaux}&\Leftrightarrow&[2\times y]+\left[(-1)\times\left(\dfrac{1}{4}\right)\right]=0\\\\&\Leftrightarrow&2y-\dfrac{1}{4}=0\\\\&\Leftrightarrow&2y=\dfrac{1}{4}\\\\&\Leftrightarrow&y=\dfrac{\dfrac{1}{4}}{2}\\\\&\Leftrightarrow&y=\dfrac{1}{4}\times\dfrac{1}{2}\\\\&\Leftrightarrow&y=\dfrac{1}{8}\end{array}$
D'où, $\boxed{y=\dfrac{1}{8}}$
3) Déterminons $x$ pour que $\vec{v}=2\vec{w}.$
Soit : $\vec{v}(4\;;\ 1-x)\ $ et $\ \vec{w}(2\;;\ -1).$
Alors, on a : $\vec{v}=2\vec{w}$ si, et seulement si, les coordonnées de $\vec{v}$ sont égales à deux fois celles de $\vec{w}.$
Ce qui signifie que : $4=2\times 2\ $ et $\ 1-x=2\times(-1)$
En résolvant l'équation $1-x=2\times(-1)$, on obtient :
$\begin{array}{rcl} 1-x=2\times(-1)&\Leftrightarrow&1-x=-2\\\\&\Leftrightarrow&-x=-2-1\\\\&\Leftrightarrow&-x=-3\\\\&\Leftrightarrow&x=3\end{array}$
Ainsi, $\boxed{x=3}$
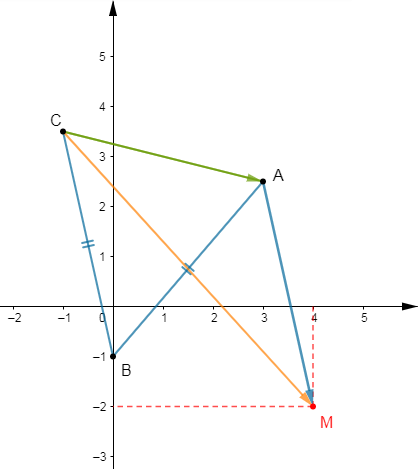
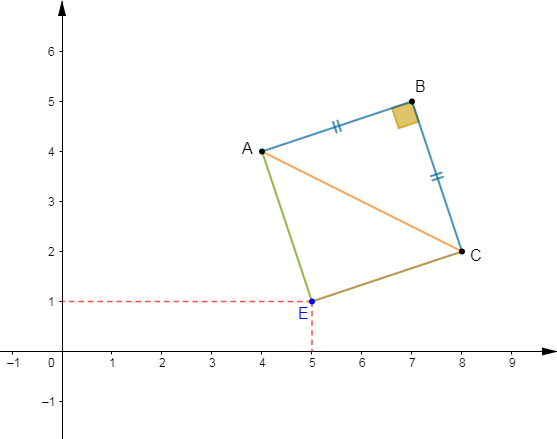
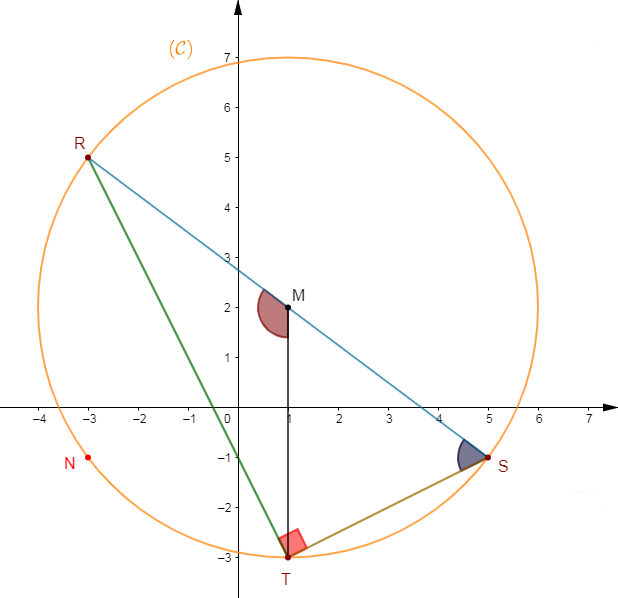
Exercice 25
Le plan est muni d'un repère orthonormal $(O\;,\ \vec{i}\;,\ \vec{j}).$
L'unité est le centimètre.
1) Plaçons les points : $A\left(3\;;\ \dfrac{5}{2}\right)\;,\ B(0\;;\ -1)\ $ et $\ C\left(-1\;;\ \dfrac{7}{2}\right)$
2) Calculons les distances $AB\ $ et $\ BC.$
Pour cela, déterminons d'abord les coordonnées des vecteurs $\overrightarrow{AB}\ $ et $\ \overrightarrow{BC}.$
On a :
$\overrightarrow{AB}\begin{pmatrix} 0-3\\\\-1-\dfrac{5}{2}\end{pmatrix}=\begin{pmatrix} -3\\\\-\dfrac{7}{2}\end{pmatrix}$
$\overrightarrow{BC}\begin{pmatrix} -1-0\\\\\dfrac{7}{2}-(-1)\end{pmatrix}=\begin{pmatrix} -1\\\\\dfrac{7}{2}+1\end{pmatrix}=\begin{pmatrix} -1\\\\\dfrac{9}{2}\end{pmatrix}$
Ainsi, les distances $AB\ $ et $\ BC$ sont données par :
$\begin{array}{rcl} AB&=&\sqrt{(-3)^{2}+\left(-\dfrac{7}{2}\right)^{2}}\\\\&=&\sqrt{9+\dfrac{49}{4}}\\\\&=&\sqrt{\dfrac{36}{4}+\dfrac{49}{4}}\\\\&=&\sqrt{\dfrac{85}{4}}\\\\&=&\dfrac{\sqrt{85}}{\sqrt{4}}\\\\&=&\dfrac{\sqrt{85}}{2}\end{array}$
Donc, $\boxed{AB=\dfrac{\sqrt{85}}{2}\;cm}Ê$
$\begin{array}{rcl} BC&=&\sqrt{(-1)^{2}+\left(\dfrac{9}{2}\right)^{2}}\\\\&=&\sqrt{1+\dfrac{81}{4}}\\\\&=&\sqrt{\dfrac{4}{4}+\dfrac{81}{4}}\\\\&=&\sqrt{\dfrac{85}{4}}\\\\&=&\dfrac{\sqrt{85}}{\sqrt{4}}\\\\&=&\dfrac{\sqrt{85}}{2}\end{array}$
Donc, $\boxed{BC=\dfrac{\sqrt{85}}{2}\;cm}Ê$
3) Déduisons-en la nature du triangle $ABC.$
D'après le résultat de la question $2)$, on a : $AB=BC$
Par conséquent, le triangle $ABC$ est isocèle en $B.$
4) Plaçons le point $M$ défini par :
$$\overrightarrow{CM}=\overrightarrow{CA}+\overrightarrow{CB}$$
Calculons les coordonnées de $M.$
Calculons d'abord les coordonnées des vecteurs $\overrightarrow{CM}\;,\ \overrightarrow{CA}\ $ et $\ \overrightarrow{CB}.$
Soit alors :
$\overrightarrow{CM}\begin{pmatrix} x_{M}-(-1)\\\\y_{M}-\dfrac{7}{2}\end{pmatrix}=\begin{pmatrix} x_{M}+1\\\\y_{M}-\dfrac{7}{2}\end{pmatrix}$
$\overrightarrow{CA}\begin{pmatrix} 3-(-1)\\\\\dfrac{5}{2}-\dfrac{7}{2}\end{pmatrix}=\begin{pmatrix} 3+1\\\\-\dfrac{2}{2}\end{pmatrix}=\begin{pmatrix} 4\\\\-1\end{pmatrix}$
$\overrightarrow{CB}=\begin{pmatrix} 0-(-1)\\\\-1-\dfrac{7}{2}\end{pmatrix}=\begin{pmatrix} 1\\\\-\dfrac{9}{2}\end{pmatrix}$
Puis, calculons les coordonnées de $\overrightarrow{CA}+\overrightarrow{CB}$
On sait que la somme de deux vecteurs a pour coordonnées la somme des coordonnées de ces deux vecteurs.
Donc, les coordonnées de $\overrightarrow{CA}+\overrightarrow{CB}$ sont données par :
$\overrightarrow{CA}+\overrightarrow{CB}\begin{pmatrix} 4+1\\\\-1-\dfrac{9}{2}\end{pmatrix}=\begin{pmatrix} 5\\\\-\dfrac{11}{2}\end{pmatrix}$
Par ailleurs, on sait que deux vecteurs sont égaux s'ils ont les mêmes coordonnées.
Donc, on a :
$\begin{array}{rcl}\overrightarrow{CM}=\overrightarrow{CA}+\overrightarrow{CB}&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{M}+1&=&5\\\\y_{M}-\dfrac{7}{2}&=&-\dfrac{11}{2}\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{M}&=&5-1\\\\y_{M}&=&-\dfrac{11}{2}+\dfrac{7}{2}\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{M}&=&4\\\\y_{M}&=&-\dfrac{4}{2}\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{M}&=&4\\\\y_{M}&=&-2\end{array}\right.\end{array}$
D'où,
$$\boxed{M\begin{pmatrix} 4\\-2\end{pmatrix}}$$

Exercice 26
Le plan est muni d'un repère orthonormal $(O\;,\ \vec{i}\;,\ \vec{j}).$
On donne : $A(4\;;\ 4)\;,\ B(7\;;\ 5)\ $ et $\ C(8\;;\ 2).$
1) Montrons que le triangle $ABC$ est rectangle et isocèle.
Calculons d'abord les distances $AB\;,\ AC\ $ et $\ BC.$
Soit : $\overrightarrow{AB}\begin{pmatrix} 7-4\\5-4\end{pmatrix}=\begin{pmatrix} 3\\1\end{pmatrix}$ alors, on a :
$\begin{array}{rcl} AB&=&\sqrt{(3)^{2}+(1)^{2}}\\\\&=&\sqrt{9+1}\\\\&=&\sqrt{10}\end{array}$
Donc, $\boxed{AB=\sqrt{10}}$
Soit : $\overrightarrow{AC}\begin{pmatrix} 8-4\\2-4\end{pmatrix}=\begin{pmatrix} 4\\-2\end{pmatrix}$ alors, on a :
$\begin{array}{rcl} AC&=&\sqrt{(4)^{2}+(-2)^{2}}\\\\&=&\sqrt{16+4}\\\\&=&\sqrt{20}\\\\&=&\sqrt{4\times 5}\\\\&=&\sqrt{4}\times\sqrt{5}\\\\&=&2\sqrt{5}\end{array}$
D'où, $\boxed{AC=2\sqrt{5}}$
Soit : $\overrightarrow{BC}\begin{pmatrix} 8-7\\2-5\end{pmatrix}=\begin{pmatrix} 1\\-3\end{pmatrix}$ alors, on a :
$\begin{array}{rcl} BC&=&\sqrt{(1)^{2}+(-3)^{2}}\\\\&=&\sqrt{1+9}\\\\&=&\sqrt{10}\end{array}$
Ainsi, $\boxed{BC=\sqrt{10}}$
On constate alors que : $AB=BC.$
Ce qui signifie que le triangle $ABC$ est isocèle en $B.$
Puis, en calculant le carré de ces distances, on obtient :
$AB^{2}=(\sqrt{10})^{2}=10$
$AC^{2}=(2\sqrt{5})^{2}=20$
$BC^{2}=(\sqrt{10})^{2}=10$
Alors, on remarque que : $10+10=20$
Ce qui signifie que : $AB^{2}+BC^{2}=AC^{2}.$
Ainsi, d'après la réciproque du théorème de Pythagore $ABC$ est un triangle rectangle en $B.$
Par conséquent, le triangle $ABC$ est rectangle et isocèle en $B.$
2) Déterminons les coordonnées de $E$ tel que $\overrightarrow{BC}=\overrightarrow{AE}.$
Soit : $\overrightarrow{AE}\begin{pmatrix} x_{E}-4\\\\y_{E}-4\end{pmatrix}.$
Comme deux vecteurs sont égaux s'ils ont les mêmes coordonnées alors, on a :
$\begin{array}{rcl}\overrightarrow{AE}=\overrightarrow{BC}&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{E}-4&=&1\\\\y_{E}-4&=&-3\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{E}&=&1+4\\\\y_{E}&=&-3+4\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{E}&=&5\\\\y_{E}&=&1\end{array}\right.\end{array}$
D'où,
$$\boxed{E\begin{pmatrix} 5\\1\end{pmatrix}}$$
3) Donnons en le justifiant, la nature exacte de $ABCE.$
D'après la question précédente, on a : $\overrightarrow{BC}=\overrightarrow{AE}$
Donc, $ABCE$ est un parallélogramme.
Par ailleurs, d'après le résultat de la question $1)$, le triangle $ABC$ est rectangle et isocèle en $B.$
Ce qui signifie que : $\overrightarrow{AB}\perp\overrightarrow{BC}\ $ et $\ AB=BC.$
Ainsi, le quadrilatère $ABCE$ est un parallélogramme dont deux côtés perpendiculaires ont même longueur.
Par conséquent, $ABCE$ est un carré.

Exercice 27
Dans un repère orthonormal dont l'unité est le centimètre, on donne les points $R(-3\;;\ 5)\;,\ S(5\;;\ -1)\ $ et $\ T(1\;;\ -3).$
1) Montrons que $RS=10.$
Calculons d'abord les coordonnées du vecteur $\overrightarrow{RS}.$
Soit : $\overrightarrow{RS}\begin{pmatrix} 5-(-3)\\-1-5\end{pmatrix}=\begin{pmatrix} 5+3\\-6\end{pmatrix}=\begin{pmatrix} 8\\-6\end{pmatrix}.$
Alors, la longueur $RS$ est donnée par :
$\begin{array}{rcl} RS&=&\sqrt{(8)^{2}+(-6)^{2}}\\\\&=&\sqrt{64+36}\\\\&=&\sqrt{100}\\\\&=&10\end{array}$
D'où, $\boxed{RS=10\;cm}$
2) Calculons les longueurs $RT\ $ et $\ ST.$ Donnons les résultats sous la forme $a\sqrt{5}.$
Soit : $\overrightarrow{RT}\begin{pmatrix} 1-(-3)\\-3-5\end{pmatrix}=\begin{pmatrix} 1+3\\-8\end{pmatrix}=\begin{pmatrix} 4\\-8\end{pmatrix}$ alors, on a :
$\begin{array}{rcl} RT&=&\sqrt{(4)^{2}+(-8)^{2}}\\\\&=&\sqrt{16+64}\\\\&=&\sqrt{80}\\\\&=&\sqrt{16\times 5}\\\\&=&\sqrt{16}\times\sqrt{5}\\\\&=&4\sqrt{5}\end{array}$
Donc, $\boxed{RT=4\sqrt{5}}$
Soit : $\overrightarrow{ST}\begin{pmatrix} 1-5\\-3-(-1)\end{pmatrix}=\begin{pmatrix} -4\\-3+1\end{pmatrix}=\begin{pmatrix} -4\\-2\end{pmatrix}$ alors, on a :
$\begin{array}{rcl} ST&=&\sqrt{(-4)^{2}+(-2)^{2}}\\\\&=&\sqrt{16+4}\\\\&=&\sqrt{20}\\\\&=&\sqrt{4\times 5}\\\\&=&\sqrt{4}\times\sqrt{5}\\\\&=&2\sqrt{5}\end{array}$
D'où, $\boxed{ST=2\sqrt{5}}$
3) Montrons que $RTS$ est un triangle rectangle.
En calculant le carré de chacune des longueurs $RS\;,\ RT\ $ et $\ ST$, on obtient :
$RS^{2}=(10)^{2}=100$
$RT^{2}=(4\sqrt{5})^{2}=80$
$ST^{2}=(2\sqrt{5})^{2}=20$
Alors, on remarque que : $80+20=100$
Ce qui signifie que : $RT^{2}+ST^{2}=RS^{2}.$
Ainsi, d'après la réciproque du théorème de Pythagore $RTS$ est un triangle rectangle en $T.$
4) Calculons la valeur exacte de l'aire de $RST$ et son périmètre.
Soit : $\mathcal{A}$ l'aire du triangle $RST.$
Comme le triangle est rectangle en $T$ alors, on a :
$\begin{array}{rcl}\mathcal{A}&=&\dfrac{RT\times ST}{2}\\\\&=&\dfrac{4\sqrt{5}\times 2\sqrt{5}}{2}\\\\&=&\dfrac{8\times 5}{2}\\\\&=&20\end{array}$
D'où, $\boxed{\mathcal{A}=20\;cm^{2}}$
Soit : $p$ le périmètre du triangle $RST.$
Alors, on a :
$\begin{array}{rcl} p&=&RT+ST+RS\\\\&=&4\sqrt{5}+2\sqrt{5}+10\\\\&=&10+6\sqrt{5}\end{array}$
Ainsi, $\boxed{p=(10+6\sqrt{5})\;cm}$
5) On appelle $(\mathcal{C})$ le cercle circonscrit au triangle $RST$ de centre $M.$
a) Exprimons $\widehat{TSR}$ en fonction de $\widehat{TMR}$
En effet, on remarque que : $\widehat{TSR}$ est un angle inscrit dans $(\mathcal{C})$ ayant pour angle au centre associé l'angle $\widehat{TMR}.$
Donc, on a : $\ 2\times\widehat{TSR}=\widehat{TMR}$
D'où, $\boxed{\widehat{TSR}=\dfrac{\widehat{TMR}}{2}}$
b) Calculons les coordonnées de $M.$
On a : $RST$ est un triangle rectangle en $T$ donc, le cercle $(\mathcal{C})$ circonscrit à ce triangle a pour centre le milieu de l'hypoténuse, $[RS].$
Comme $M$ est le centre de ce cercle, alors, $M$ a pour coordonnées :
$\begin{array}{rcl} x_{M}&=&\dfrac{x_{R}+x_{S}}{2}\\\\&=&\dfrac{-3+5}{2}\\\\&=&\dfrac{2}{2}\\\\&=&1\end{array}$
Donc, $\boxed{x_{M}=1}$
$\begin{array}{rcl} y_{M}&=&\dfrac{y_{R}+y_{S}}{2}\\\\&=&\dfrac{5-1}{2}\\\\&=&\dfrac{4}{2}\\\\&=&2\end{array}$
Donc, $\boxed{y_{M}=2}$
D'où,
$$\boxed{M\begin{pmatrix} 1\\2\end{pmatrix}}$$
c) Calculons le rayon du cercle $(\mathcal{C}).$
Soit $r$ le rayon de ce cercle.
Comme $[RS]$ est un diamètre de $(\mathcal{C})$ alors, le rayon $r$ est donné par : $r=\dfrac{RS}{2}$
D'où, $\boxed{r=\dfrac{10}{2}=5\;cm}$
d) Démontrons par calcul que le point $N(-3\;;\ -1)$ appartient au cercle $(\mathcal{C}).$
Pour démontrer que le point $N(-3\;;\ -1)$ appartient au cercle $(\mathcal{C})$, il suffit juste de montrer que la longueur $MN$ est égale au rayon de ce cercle.
Calculons alors la longueur $MN.$
Soit : $\overrightarrow{MN}\begin{pmatrix} -3-1\\-1-2\end{pmatrix}=\begin{pmatrix} -4\\-3\end{pmatrix}$
Ainsi, on a :
$\begin{array}{rcl} MN&=&\sqrt{(-4)^{2}+(-3)^{2}}\\\\&=&\sqrt{16+9}\\\\&=&\sqrt{25}\\\\&=&5\end{array}$
D'où, $\boxed{MN=5\;cm}$
On remarque alors que la longueur $MN$ est égale au rayon du cercle $(\mathcal{C})$ de centre $M.$
Par conséquent, le point $N$ appartient à ce cercle.

Exercice 28
1) Déterminons une équation générale de chacune des droites décrites ci-dessous :
a) Droite passant par les points $A(2\;;\ -2)\ $ et $\ B(4\;;\ -1).$
Soit $M\begin{pmatrix} x\\y\end{pmatrix}\in(AB)$ alors, $\overrightarrow{AM}\ $ et $\ \overrightarrow{AB}$ sont colinéaires.
On a :
$\overrightarrow{AM}\begin{pmatrix} x-2\\y-(-2)\end{pmatrix}=\begin{pmatrix} x-2\\y+2\end{pmatrix}$
$\overrightarrow{AB}\begin{pmatrix} 4-2\\-1-(-2)\end{pmatrix}=\begin{pmatrix} 2\\1\end{pmatrix}$
Ainsi, en appliquant la condition de colinéarité, on obtient :
$\begin{array}{rcl}\overrightarrow{AM}\ \text{ et }\ \overrightarrow{AB}\ \text{ sont colinéaires}&\Leftrightarrow&(x_{_{\overrightarrow{AM}}}\times y_{_{\overrightarrow{AB}}})-(x_{_{\overrightarrow{AB}}}\times y_{_{\overrightarrow{AM}}})=0\\\\&\Leftrightarrow&[(x-2)\times 1]-[2\times(y+2)]=0\\\\&\Leftrightarrow&x-2-2y-4=0\\\\&\Leftrightarrow&x-2y-6=0\end{array}$
D'où, une équation générale de la droite passant par les points $A(2\;;\ -2)\ $ et $\ B(4\;;\ -1)$ est donnée par :
$$\boxed{(AB)\ :\ x-2y-6=0}$$
b) Droite $(\mathcal{D})$ passant par $A(2\;;\ 2)$ et parallèle à $(BC)$ avec, $B(0\;;\ 2)\ $ et $\ C(3\;;\ 8)$
Soit $\overrightarrow{BC}$ un vecteur directeur de la droite $(BC)\ $ et $\ M\begin{pmatrix} x\\y\end{pmatrix}\in(\mathcal{D}).$
$(\mathcal{D})$ parallèle à $(BC)$ signifie que les vecteurs $\overrightarrow{AM}\ $ et $\ \overrightarrow{BC}$ sont colinéaires.
On a :
$\overrightarrow{AM}\begin{pmatrix} x-2\\y-2\end{pmatrix}$
$\overrightarrow{BC}\begin{pmatrix} 3-0\\8-2\end{pmatrix}=\begin{pmatrix} 3\\6\end{pmatrix}$
Ainsi, en appliquant la condition de colinéarité, on obtient :
$\begin{array}{rcl}\overrightarrow{AM}\ \text{ et }\ \overrightarrow{BC}\ \text{ sont colinéaires}&\Leftrightarrow&(x_{_{\overrightarrow{AM}}}\times y_{_{\overrightarrow{BC}}})-(x_{_{\overrightarrow{BC}}}\times y_{_{\overrightarrow{AM}}})=0\\\\&\Leftrightarrow&[(x-2)\times 6]-[3\times(y-2)]=0\\\\&\Leftrightarrow&6x-12-3y+6=0\\\\&\Leftrightarrow&6x-3y-6=0\\\\&\Leftrightarrow&2x-y-2=0\end{array}$
D'où, une équation générale de la droite $(\mathcal{D})$ passant par $A(2\;;\ 2)$ et parallèle à $(BC)$ est donnée par :
$$\boxed{(\mathcal{D})\ :\ 2x-y-2=0}$$
c) Droite $(\Delta)$ passant par $G(-3\;;\ 2)$ et perpendiculaire à $(EF)$ avec, $E(-1\;;\ 4)\ $ et $\ F(1\;;\ 1)$
Soit $\overrightarrow{EF}$ un vecteur directeur de la droite $(EF)\ $ et $\ M\begin{pmatrix} x\\y\end{pmatrix}\in(\Delta).$
Comme $(\Delta)$ est perpendiculaire à la droite $(EF)$ alors, les vecteurs $\overrightarrow{GM}\ $ et $\ \overrightarrow{EF}$ sont orthogonaux.
On a :
$\overrightarrow{GM}\begin{pmatrix} x-(-3)\\y-2\end{pmatrix}=\begin{pmatrix} x+3\\y-2\end{pmatrix}$
$\overrightarrow{EF}\begin{pmatrix} 1-(-1)\\1-4\end{pmatrix}=\begin{pmatrix} 2\\-3\end{pmatrix}$
Ainsi, en appliquant la condition d'orthogonalité, on obtient :
$\begin{array}{rcl}\overrightarrow{GM}\ \text{ et }\ \overrightarrow{EF}\ \text{ sont orthogonaux}&\Leftrightarrow&(x_{_{\overrightarrow{GM}}}\times x_{_{\overrightarrow{EF}}})+(y_{_{\overrightarrow{GM}}}\times y_{_{\overrightarrow{EF}}})=0\\\\&\Leftrightarrow&[(x+3)\times 2]+[(y-2)\times(-3)]=0\\\\&\Leftrightarrow&2x+6-3y+6=0\\\\&\Leftrightarrow&2x-3y+12=0\end{array}$
D'où, une équation générale de la droite $(\Delta)$ passant par $G(-3\;;\ 2)$ et perpendiculaire à $(EF)$ est donnée par :
$$\boxed{(\Delta)\ :\ 2x-3y+12=0}$$
d) Droite $(\mathcal{L})$ passant par $A(3\;;\ 1)$ et de vecteur directeur $\vec{u}(-2\;;\ 5).$
Une équation générale de la droite $(\mathcal{L})$ est de la forme :
$$ax+by+c=0$$
avec : $a\;,\ b\;,\ $ et $\ c$ des nombres réels tels que $a\neq 0\ $ et/ou $\ b\neq 0$
Dans ce cas, les coordonnées du vecteur directeur de $(\mathcal{L})$ sont de la forme :
$$\begin{pmatrix} -b\\a\end{pmatrix}$$
Or, $(\mathcal{L})$ a pour vecteur directeur $\vec{u}\begin{pmatrix} -2\\5\end{pmatrix}$ donc, par identification, on trouve :
$$\left\lbrace\begin{array}{rcl} -b&=&-2\\a&=&5\end{array}\right.\ \Leftrightarrow\ \left\lbrace\begin{array}{rcl} b&=&2\\a&=&5\end{array}\right.$$
En remplaçant ces valeurs de $a\ $ et $\ b$ dans l'équation générale de la droite $(\mathcal{L})$, on obtient :
$$5x+2y+c=0$$
Comme $(\mathcal{L})$ passe par $A(3\;;\ 1)$ alors, les coordonnées de ce point vérifient l'équation générale de $(\mathcal{L}).$
Ainsi,
$\begin{array}{rcl} 5\times x_{A}+2\times y_{A}+c=0&\Leftrightarrow&5\times 3+2\times 1+c=0\\\\&\Leftrightarrow&15+2+c=0\\\\&\Leftrightarrow&17+c=0\\\\&\Leftrightarrow&c=-17\end{array}$
Par suite, une équation générale de la droite $(\mathcal{L})$ passant par $A(3\;;\ 1)$ et de vecteur directeur $\vec{u}(-2\;;\ 5)$ est donnée par :
$$\boxed{(\mathcal{L})\ :\ 5x+2y-17=0}$$
2) Déterminons une équation réduite de chacune des droites données ci-dessous.
a) Droite passant par les points $A(4\;;\ 3)\ $ et $\ B(0\;;\ 1)$
Une équation réduite de la droite passant par les points $A(4\;;\ 3)\ $ et $\ B(0\;;\ 1)$ est de la forme :
$$y=ax+b$$
Soit : $\overrightarrow{AB}$ vecteur directeur de la droite $(AB)$
On a : $\overrightarrow{AB}\begin{pmatrix} 0-4\\1-3\end{pmatrix}=\begin{pmatrix} -4\\-2\end{pmatrix}$
Alors, le coefficient directeur de la droite $(AB)$ est :
$$a=\dfrac{-2}{-4}=\dfrac{1}{2}$$
Donc, $(AB)\ :\ y=\dfrac{1}{2}x+b$
Comme $(AB)$ passe par $B$ alors, les coordonnées de ce point vérifient l'équation réduite de $(AB).$
Ainsi, $1=\dfrac{1}{2}\times 0+b\ \Rightarrow\ b=1$
D'où, une équation réduite de la droite passant par les points $A(4\;;\ 3)\ $ et $\ B(0\;;\ 1)$ est donnée par :
$$\boxed{(AB)\ :\ y=\dfrac{1}{2}x+1}$$
b) Droite $(\mathcal{L})$ passant par $H(7\;;\ -2)$ et de coefficient directeur $-1.$
Une équation réduite de la droite $(\mathcal{L})$ passant par $H(7\;;\ -2)$ et de coefficient directeur $-1$ est de la forme :
$$(\mathcal{L})\ :\ y=-x+b$$
Or, la droite $(\mathcal{L})$ passe par $H(7\;;\ -2)$ donc, les coordonnées de ce point vérifient l'équation réduite de $(\mathcal{L}).$
Ce qui se traduit par, $-2=-7+b\ \Rightarrow\ b=-2+7=5$
Ainsi, une équation réduite de la droite $(\mathcal{L})$ passant par $H(7\;;\ -2)$ et de coefficient directeur $-1$ est donnée par :
$$\boxed{(\mathcal{L})\ :\ y=-x+5}$$
c) Droite $(\mathcal{D'})$ passant par $K(4\;;\ 5)$ et perpendiculaire à la droite $(\mathcal{D})\ :\ y=3x+1.$
Une équation réduite de la droite $(\mathcal{D'})$ est de la forme :
$$y=ax+b$$
On a : $(\mathcal{D})$ d'équation $y=3x+1$ donc, son coefficient directeur est égal à $3.$
Comme $(\mathcal{D'})$ est perpendiculaire à $(\mathcal{D})$ alors, les coefficients directeurs de ces deux droites vérifient :
$$a\times 3=-1\ \Rightarrow\ a=\dfrac{-1}{3}$$
Par suite, une équation réduite de la droite $(\mathcal{D'})$ est de la forme :
$$y=\dfrac{-1}{3}x+b$$
Par ailleurs, la droite $(\mathcal{D'})$ passe par $K(4\;;\ 5)$ donc, les coordonnées de ce point vérifient l'équation réduite de $(\mathcal{D'}).$
Ainsi,
$\begin{array}{rcl} 5=\dfrac{-1}{3}\times 4+b&\Rightarrow&b=5+\dfrac{4}{3}\\\\&\Rightarrow&b=\dfrac{15}{3}+\dfrac{4}{3}\\\\&\Rightarrow&b=\dfrac{15+4}{3}\\\\&\Rightarrow&b=\dfrac{19}{3}\end{array}$
D'où, une équation réduite de la droite $(\mathcal{D'})$ passant par $K(4\;;\ 5)$ et perpendiculaire à la droite $(\mathcal{D})\ :\ y=3x+1$ est donnée par :
$$\boxed{(\mathcal{D'})\ :\ y=-\dfrac{1}{3}x+\dfrac{19}{3}}$$
d) Droite $(\Delta')$ passant par $S(1\;;\ 2)$ et parallèle à la droite $(\Delta)\ :\ y=x-6.$
Une équation réduite de la droite $(\Delta')$ est de la forme :
$$y=ax+b$$
Soit $(\Delta)$ d'équation $y=x-6$ donc, son coefficient directeur est égal à $1.$
Comme $(\Delta')\ $ et $\ (\Delta)$ sont parallèles alors, les deux droites ont même coefficient directeur.
Donc, $a=1$
Par suite, une équation réduite de la droite $(\Delta')$ est de la forme :
$$y=x+b$$
Par ailleurs, la droite $(\Delta')$ passe par $S$ donc, les coordonnées de ce point vérifient l'équation réduite de $(\Delta').$
Ainsi, $2=1+b\ \Rightarrow\ b=2-1=1$
D'où, une équation réduite de la droite $(\Delta')$ passant par $S(1\;;\ 2)$ et parallèle à la droite $(\Delta)\ :\ y=x-6.$ est donnée par :
$$\boxed{(\Delta')\ :\ y=x+1}$$
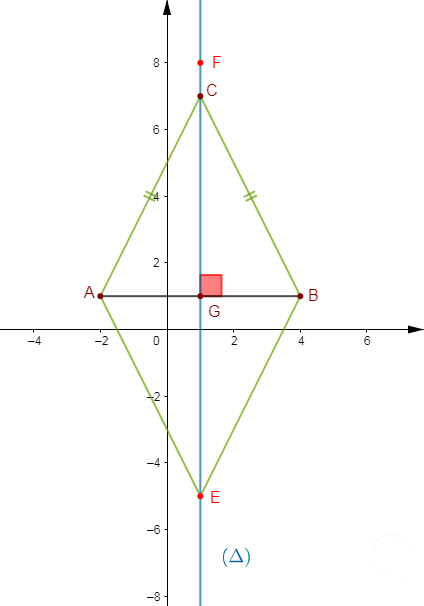
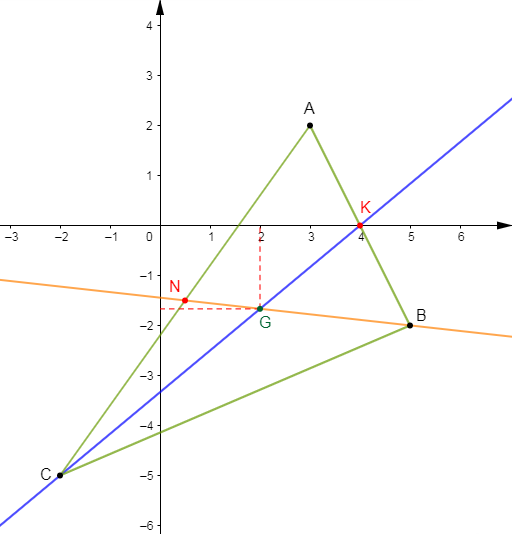
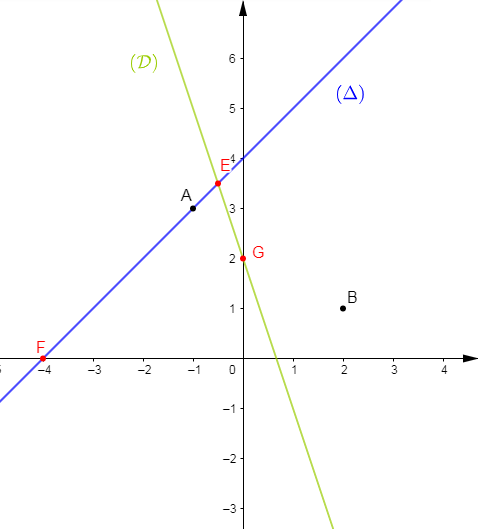
Exercice 29
On donne les points $A(-2\;;\ 1)\;;\ B(4\;;\ 1)\ $ et $\ C(1\;;\ 7).$
1) Calculons $AC\ $ et $\ BC$ puis déduisons-en que $C$ appartient à la médiatrice de $[AB].$
Soit : $\overrightarrow{AC}\begin{pmatrix} 1-(-2)\\7-1\end{pmatrix}=\begin{pmatrix} 3\\6\end{pmatrix}$ alors, on a :
$\begin{array}{rcl} AC&=&\sqrt{(3)^{2}+(6)^{2}}\\\\&=&\sqrt{9+36}\\\\&=&\sqrt{45}\\\\&=&\sqrt{9\times 5}\\\\&=&\sqrt{9}\times\sqrt{5}\\\\&=&3\sqrt{5}\end{array}$
Donc, $\boxed{AC=3\sqrt{5}}$
Soit : $\overrightarrow{BC}\begin{pmatrix} 1-4\\7-1\end{pmatrix}=\begin{pmatrix} -3\\6\end{pmatrix}$ alors, on a :
$\begin{array}{rcl} BC&=&\sqrt{(-3)^{2}+(6)^{2}}\\\\&=&\sqrt{9+36}\\\\&=&\sqrt{45}\\\\&=&\sqrt{9\times 5}\\\\&=&\sqrt{9}\times\sqrt{5}\\\\&=&3\sqrt{5}\end{array}$
Donc, $\boxed{BC=3\sqrt{5}}$
Ainsi, on constate que : $AC=BC$
Ce qui signifie que le point $C$ est équidistant des points $A\ $ et $\ B.$
Par conséquent, $C$ appartient à la médiatrice du segment $[AB].$
2) Déterminons l'équation de $(\Delta)$ perpendiculaire à $(AB)$ et passant par $C.$
Soit $M\begin{pmatrix} x\\y\end{pmatrix}$ appartenant à la droite $(\Delta)$
Donc, $(\Delta)$ passe par $C\ $ et $\ M$
Ainsi, $(\Delta)$ est perpendiculaire à $(AB)$ si, et seulement si, $\overrightarrow{AB}\ $ et $\ \overrightarrow{CM}$ sont orthogonaux.
Soit : $\overrightarrow{AB}\begin{pmatrix} 4-(-2)\\1-1\end{pmatrix}=\begin{pmatrix} 6\\0\end{pmatrix}$
$\overrightarrow{CM}\begin{pmatrix} x-1\\y-7\end{pmatrix}$
Alors, en appliquant la condition d'orthogonalité, on obtient :
$\begin{array}{rcl}\overrightarrow{AB}\ \text{ et }\ \overrightarrow{CM}\ \text{ sont orthogonaux}&\Leftrightarrow&(x_{_{\overrightarrow{AB}}}\times x_{_{\overrightarrow{CM}}})+(y_{_{\overrightarrow{AB}}}\times y_{_{\overrightarrow{CM}}})=0\\\\&\Leftrightarrow&\left[6\times(x-1)\right]+[0\times(y-7)]=0\\\\&\Leftrightarrow&6x-6+0y+0=0\\\\&\Leftrightarrow&6x+0y-6=0\end{array}$
D'où, une équation de la droite $(\Delta)$ perpendiculaire à $(AB)$ et passant par $C$ est donnée par :
$$\boxed{(\Delta)\ :\ 6x+0y-6=0}$$
On peut encore écrire :
$$\boxed{(\Delta)\ :\ x=1}$$
3) Déterminons l'abscisse $x_{E}$ du point $E$ de $(\Delta)$ d'ordonnée $-5$ puis l'abscisse $x_{F}$ du point $F$ de $(\Delta)$ d'ordonnée $8.$
Comme $E$ est un point de $(\Delta)$ alors, ses coordonnées vérifient l'équation de $(\Delta).$
Donc, on a :
$\begin{array}{rcl} 6\times x_{E}+0\times y_{E}-6=0&\Leftrightarrow&6x_{E}+0-6=0\\\\&\Leftrightarrow&6x_{E}=6\\\\&\Leftrightarrow&x_{E}=\dfrac{6}{6}\\\\&\Leftrightarrow&x_{E}=1\end{array}$
Ainsi, $\boxed{x_{E}=1}$
Comme $F$ appartient à $(\Delta)$ alors, ses coordonnées vérifient l'équation de $(\Delta).$
Ainsi, on a :
$\begin{array}{rcl} 6\times x_{F}+0\times y_{F}-6=0&\Leftrightarrow&6x_{F}+0-6=0\\\\&\Leftrightarrow&6x_{F}=6\\\\&\Leftrightarrow&x_{F}=\dfrac{6}{6}\\\\&\Leftrightarrow&x_{F}=1\end{array}$
Donc, $\boxed{x_{F}=1}$
On constate alors que ces deux points ont la même abscisse que le point $C.$
4) Calculons les coordonnées du point $G$ milieu de $[AB].$
Comme $G$ est milieu de $[AB]$ alors, ses coordonnées sont données par :
$\begin{array}{rcl} x_{G}&=&\dfrac{x_{A}+x_{B}}{2}\\\\&=&\dfrac{-2+4}{2}\\\\&=&\dfrac{2}{2}\\\\&=&1\end{array}$
Donc, $\boxed{x_{G}=1}$
$\begin{array}{rcl} y_{G}&=&\dfrac{y_{A}+y_{B}}{2}\\\\&=&\dfrac{1+1}{2}\\\\&=&\dfrac{2}{2}\\\\&=&1\end{array}$
Donc, $\boxed{y_{G}=1}$
D'où,
$$\boxed{G\begin{pmatrix} 1\\1\end{pmatrix}}$$
5) Justifions que le quadrilatère $ACBE$ est un losange
Montrons d'abord que $ACBE$ est un parallélogramme.
Pour cela, vérifions que $G$ est aussi milieu de $[CE].$
On a :
$\begin{array}{rcl} \dfrac{x_{C}+x_{E}}{2}&=&\dfrac{1+1}{2}\\\\&=&\dfrac{2}{2}\\\\&=&1\end{array}$
Donc, $\boxed{\dfrac{x_{C}+x_{E}}{2}=x_{G}}$
$\begin{array}{rcl} \dfrac{y_{C}+y_{E}}{2}&=&\dfrac{-5+7}{2}\\\\&=&\dfrac{2}{2}\\\\&=&1\end{array}$
Donc, $\boxed{\dfrac{y_{C}+y_{E}}{2}=y_{G}}$
Ce qui justifie que $G$ est milieu de $[CE].$
Ainsi, le quadrilatère $ACBE$ a ses diagonales de même milieu.
Par conséquent, c'est un parallélogramme.
Par ailleurs, comme $(\Delta)$ est perpendiculaire à $(AB)$ et que $C\ $ et $\ E$ appartiennent à $(\Delta)$ alors, $(CE)$ est perpendiculaire à $(AB).$
Ainsi, le quadrilatère $ACBE$ est un parallélogramme dont les diagonales sont perpendiculaires.
Donc, c'est un losange.

Exercice 30
On donne les points $A(3\;;\ 2)\;;\ B(5\;;\ -2)\ $ et $\ C(-2\;;\ -5).$
1) Calculons les coordonnées de $K$ milieu de $[AB]$ et celles de $N$ milieu de $[AC].$
Comme $K$ est milieu de $[AB]$ alors, ses coordonnées sont données par :
$$x_{K}=\dfrac{x_{A}+x_{B}}{2}\ \text{ et }\ y_{K}=\dfrac{y_{A}+y_{B}}{2}$$
Soit alors :
$\begin{array}{rcl} x_{K}&=&\dfrac{x_{A}+x_{B}}{2}\\\\&=&\dfrac{3+5}{2}\\\\&=&\dfrac{8}{2}\\\\&=&4\end{array}$
Donc, $\boxed{x_{K}=4}$
$\begin{array}{rcl} y_{K}&=&\dfrac{y_{A}+y_{B}}{2}\\\\&=&\dfrac{2-2}{2}\\\\&=&\dfrac{0}{2}\\\\&=&0\end{array}$
Donc, $\boxed{y_{K}=0}$
D'où,
$$\boxed{K\begin{pmatrix} 4\\0\end{pmatrix}}$$
Comme $N$ est milieu de $[AC]$ alors, ses coordonnées sont données par :
$$x_{N}=\dfrac{x_{A}+x_{C}}{2}\ \text{ et }\ y_{N}=\dfrac{y_{A}+y_{C}}{2}$$
Ainsi, on a :
$\begin{array}{rcl} x_{N}&=&\dfrac{x_{A}+x_{C}}{2}\\\\&=&\dfrac{3-2}{2}\\\\&=&\dfrac{1}{2}\end{array}$
Donc, $\boxed{x_{C}=\dfrac{1}{2}}$
$\begin{array}{rcl} y_{N}&=&\dfrac{y_{A}+y_{C}}{2}\\\\&=&\dfrac{2-5}{2}\\\\&=&\dfrac{-3}{2}\end{array}$
Donc, $\boxed{y_{N}=-\dfrac{3}{2}}$
D'où,
$$\boxed{N\begin{pmatrix} \dfrac{1}{2}\\\\-\dfrac{3}{2}\end{pmatrix}}$$
2) Dans le triangle $ABC$, les droites $(CK)\ $ et $\ (BN)$ représentent des médianes.
En effet, ces droites passent respectivement par les sommets $C\ $ et $\ B$ du triangle $ABC$ et par les milieux respectifs $K\ $ et $\ N$ des côtés opposés à ces sommets.
Par conséquent, les droites $(CK)\ $ et $\ (BN)$ sont des médianes du triangle $ABC.$
3) Déterminons une équation de $(CK)$ et une équation de $(BN).$
$-\ $ équation de la droite $(CK)$
Soit $M\begin{pmatrix} x\\y\end{pmatrix}$ appartenant à $(CK)$
Donc, la droite $(CK)$ passe par $C\;,\ K\ $ et $\ M$
Ainsi, les vecteurs $\overrightarrow{CK}\ $ et $\ \overrightarrow{CM}$ sont colinéaires.
Soit : $\overrightarrow{CK}\begin{pmatrix} 4-(-2)\\0-(-5)\end{pmatrix}=\begin{pmatrix} 6\\5\end{pmatrix}$
$\overrightarrow{CM}\begin{pmatrix} x-(-2)\\y-(-5)\end{pmatrix}=\begin{pmatrix} x+2\\y+5\end{pmatrix}$
Alors, en appliquant la condition de colinéarité, on obtient :
$\begin{array}{rcl}\overrightarrow{CK}\ \text{ et }\ \overrightarrow{CM}\ \text{ sont colinéaires}&\Leftrightarrow&(x_{_{\overrightarrow{CK}}}\times y_{_{\overrightarrow{CM}}})-(x_{_{\overrightarrow{CM}}}\times y_{_{\overrightarrow{CK}}})=0\\\\&\Leftrightarrow&\left[6\times(y+5)\right]-[(x+2)\times 5]=0\\\\&\Leftrightarrow&6y+30-5x-10=0\\\\&\Leftrightarrow&-5x+6y+20=0\end{array}$
D'où, une équation de la droite $(CK)$ est donnée par :
$$\boxed{(CK)\ :\ -5x+6y+20=0}$$
$-\ $ équation de la droite $(BN)$
Choisissons alors un point $P\begin{pmatrix} x\\y\end{pmatrix}$ appartenant à $(BN).$
La droite $(BN)$ passe donc par $B\;,\ N\ $ et $\ P$
Ainsi, les vecteurs $\overrightarrow{BN}\ $ et $\ \overrightarrow{BP}$ sont colinéaires.
Soit : $\overrightarrow{BN}\begin{pmatrix} \dfrac{1}{2}-5\\\\-\dfrac{3}{2}-(-2)\end{pmatrix}=\begin{pmatrix} \dfrac{1}{2}-\dfrac{10}{2}\\\\-\dfrac{3}{2}+\dfrac{4}{2}\end{pmatrix}=\begin{pmatrix}-\dfrac{9}{2}\\\\\dfrac{1}{2}\end{pmatrix}$
$\overrightarrow{BP}\begin{pmatrix} x-5\\y-(-2)\end{pmatrix}=\begin{pmatrix} x-5\\y+2\end{pmatrix}$
Alors, en appliquant la condition de colinéarité, on obtient :
$\begin{array}{rcl}\overrightarrow{BN}\ \text{ et }\ \overrightarrow{BP}\ \text{ sont colinéaires}&\Leftrightarrow&(x_{_{\overrightarrow{BN}}}\times y_{_{\overrightarrow{BP}}})-(x_{_{\overrightarrow{BP}}}\times y_{_{\overrightarrow{BN}}})=0\\\\&\Leftrightarrow&\left[-\dfrac{9}{2}\times(y+2)\right]-\left[(x-5)\times\dfrac{1}{2}\right]=0\\\\&\Leftrightarrow&-\dfrac{9}{2}y-\dfrac{18}{2}-\dfrac{1}{2}x+\dfrac{5}{2}=0\\\\&\Leftrightarrow&-\dfrac{1}{2}x-\dfrac{9}{2}y-\dfrac{13}{2}=0\\\\&\Leftrightarrow&\dfrac{x+9y+13}{-2}=0\\\\&\Leftrightarrow&x+9y+13=-2\times 0\\\\&\Leftrightarrow&x+9y+13=0\end{array}$
D'où, une équation de la droite $(BN)$ est donnée par :
$$\boxed{(BN)\ :\ x+9y+13=0}$$
4) Soit $G$ le centre de gravité du triangle $ABC.$
Plaçons le point $G$ puis calculons ses coordonnées.
En effet, on sait que le centre de gravité d'un triangle est le point de rencontre de ses trois médianes.
Or, les droites $(CK)\ $ et $\ (BN)$ sont des médianes du triangle $ABC.$
Donc, $G$ est le point d'intersection de ces deux droites.
Ainsi, ses coordonnées sont solutions du système d'équations formé par les équations respectives des droites $(CK)\ $ et $\ (BN).$
Soit alors, à résoudre le système suivant :
$$\left\lbrace\begin{array}{rclr} -5x+6y+20&=&0&\quad(1)\\\\x+9y+13&=&0&\quad(2)\end{array}\right.$$
En multipliant l'équation $(2)$ par $5$, on obtient alors le système suivant :
$$\left\lbrace\begin{array}{rclr} -5x+6y+20&=&0&\quad(1)\\\\5x+45y+65&=&0&\quad(3)\end{array}\right.$$
Par addition des équations $(1)\ $ et $\ (3)$, on trouve :
$\begin{array}{rcl} \text{équation }(1)+\text{équation }(3)&\Leftrightarrow&(-5x+6y+20)+(5x+45y+65)=0+0\\\\&\Leftrightarrow&-5x+6y+20+5x+45y+65=0\\\\&\Leftrightarrow&51y+85=0\\\\&\Leftrightarrow&51y=-85\\\\&\Leftrightarrow&y=\dfrac{-85}{51}\\\\&\Leftrightarrow&y=-\dfrac{17\times 5}{17\times 3}\\\\&\Leftrightarrow&y=-\dfrac{5}{3}\end{array}$
Donc, $\boxed{y=-\dfrac{5}{3}}$
Ensuite, en remplaçant cette valeur de $y$ dans l'équation $(2)$, on trouve :
$\begin{array}{rcl} x+9\times\left(-\dfrac{5}{3}\right)+13=0&\Rightarrow&x-\dfrac{45}{3}+13=0\\\\&\Rightarrow&x-15+13=0\\\\&\Rightarrow&x-2=0\\\\&\Rightarrow&x=2\end{array}$
Donc, $\boxed{x=2}$
D'où, $S=\left\lbrace\left(2\;;\ -\dfrac{5}{3}\right)\right\rbrace$
Ainsi, les coordonnées de $G$ sont données par :
$$\boxed{G\begin{pmatrix} 2\\\\-\dfrac{5}{3}\end{pmatrix}}$$
5) On donne :
$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\vec{0}.$
Retrouvons les coordonnées de $G$ à partir de cette relation.
En effet, utilisons la relation de Chasles en introduisant l'origine $O$ du repère.
On a alors :
$\overrightarrow{GA}=\overrightarrow{GO}+\overrightarrow{OA}$
$\overrightarrow{GB}=\overrightarrow{GO}+\overrightarrow{OB}$
$\overrightarrow{GC}=\overrightarrow{GO}+\overrightarrow{OC}$
Ainsi, en remplaçant, on obtient :
$\begin{array}{rcl} \overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\vec{0}&\Leftrightarrow&\left(\overrightarrow{GO}+\overrightarrow{OA}\right)+\left(\overrightarrow{GO}+\overrightarrow{OB}\right)+\left(\overrightarrow{GO}+\overrightarrow{OC}\right)=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{GO}+\overrightarrow{OA}+\overrightarrow{GO}+\overrightarrow{OB}+\overrightarrow{GO}+\overrightarrow{OC}=\vec{0}\\\\&\Leftrightarrow&3\overrightarrow{GO}+\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\vec{0}\\\\&\Leftrightarrow&3\overrightarrow{GO}=-\overrightarrow{OA}-\overrightarrow{OB}-\overrightarrow{OC}\\\\&\Leftrightarrow&\overrightarrow{GO}=\dfrac{-\overrightarrow{OA}-\overrightarrow{OB}-\overrightarrow{OC}}{3}\\\\&\Leftrightarrow&\overrightarrow{GO}=-\dfrac{1}{3}\left(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\right)\\\\&\Leftrightarrow&\overrightarrow{OG}=\dfrac{1}{3}\left(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\right)\end{array}$
Donc, $\boxed{\overrightarrow{OG}=\dfrac{1}{3}\left(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\right)}$
Ce qui signifie que les coordonnées de $G$ sont données par :
$$x_{G}=\dfrac{x_{A}+x_{B}+x_{C}}{3}\ \text{ et }\ y_{G}=\dfrac{y_{A}+y_{B}+y_{C}}{3}$$
Ce qui donne alors :
$\begin{array}{rcl} x_{G}&=&\dfrac{x_{A}+x_{B}+x_{C}}{3}\\\\&=&\dfrac{3+5-2}{3}\\\\&=&\dfrac{6}{3}\\\\&=&2\end{array}$
Donc, $\boxed{x_{G}=2}$
$\begin{array}{rcl} y_{G}&=&\dfrac{y_{A}+y_{B}+y_{C}}{3}\\\\&=&\dfrac{2-2-5}{3}\\\\&=&\dfrac{-5}{3}\end{array}$
Alors, $\boxed{y_{G}=-\dfrac{5}{3}}$
On retrouve bien les coordonnée de $G.$

Exercice 31
On donne les points $A(-1\;;\ 3)\;,\ B(2\;;\ 1)$ et les droites $(\Delta)\ :\ x-y+4=0\ $ et $\ (\mathcal{D})\ :\ y=-3x+2$
1) $A$ appartient à la droite $(\Delta)$ mais $B$ n'appartient pas à la droite $(\mathcal{D})$
En effet, en remplaçant les coordonnées de $A$ dans l'équation de $(\Delta)$, on obtient :
$\begin{array}{rcl}x_{A}-y_{A}+4&=&-1-3+4\\\\&=&-4+4\\\\&=&0\end{array}$
Donc, $\boxed{x_{A}-y_{A}+4=0}$
Ce qui signifie que les coordonnées de $A$ vérifient l'équation de $(\Delta).$
D'où, le point $A$ appartient à la droite $(\Delta).$
De la même manière, en remplaçant les coordonnées de $B$ dans l'équation de $(\mathcal{D})$, on obtient :
$\begin{array}{rcl} 1&=&-3\times 2+2\\\\&=&-6+2\\\\&=&-4\end{array}$
Donc, on trouve : $1=-4$ ; ce qui est faux.
D'où, $\boxed{y_{B}\neq -2x_{B}+2}$
Ce qui signifie que les coordonnées de $B$ ne vérifient pas l'équation de $(\mathcal{D}).$
Par conséquent, le point $B$ n'appartient pas à la droite $(\mathcal{D}).$
2) Calculons les coordonnées de $E$, point d'intersection de $(\Delta)\ $ et $\ (\mathcal{D}).$
Comme $E$ est le point d'intersection de $(\Delta)\ $ et $\ (\mathcal{D})$ alors, ses coordonnées sont solutions du système d'équations formé par les équations respectives des droites $(\Delta)\ $ et $\ (\mathcal{D}).$
Soit alors, à résoudre le système suivant :
$$\left\lbrace\begin{array}{rclr} x-y+4&=&0&\quad(1)\\\\y&=&-3x+2&\quad(2)\end{array}\right.$$
Par substitution, on remplace $y$ dans l'équation $(1)$ par son expression dans l'équation $(2).$
On obtient alors :
$\begin{array}{rcl} x-(-3x+2)+4=0&\Rightarrow&x+3x-2+4=0\\\\&\Rightarrow&4x+2=0\\\\&\Rightarrow&4x=-2\\\\&\Rightarrow&x=\dfrac{-2}{4}\\\\&\Rightarrow&x=-\dfrac{1}{2}\end{array}$
Donc, $\boxed{x=-\dfrac{1}{2}}$
Ensuite, en remplaçant cette valeur de $x$ dans l'équation $(2)$, on trouve :
$\begin{array}{rcl} y&=&-3\times\left(-\dfrac{1}{2}\right)+2\\\\&=&\dfrac{3}{2}+2\\\\&=&\dfrac{3}{2}+\dfrac{4}{2}\\\\&=&\dfrac{7}{2}\end{array}$
Donc, $\boxed{y=\dfrac{7}{2}}$
D'où, $S=\left\lbrace\left(-\dfrac{1}{2}\;;\ \dfrac{7}{2}\right)\right\rbrace$
Par conséquent, les coordonnées de $E$ sont données par :
$$\boxed{E\begin{pmatrix} -\dfrac{1}{2}\\\\\dfrac{7}{2}\end{pmatrix}}$$
3) Calculons les coordonnées de $F$, point d'intersection de $(\Delta)$ avec l'axe des abscisses.
Comme $F$ est le point d'intersection de $(\Delta)$ avec l'axe des abscisses alors, $F$ appartient à l'axe des abscisses.
Donc, son ordonnée est égale à $0.$
D'où, $\boxed{y_{F}=0}$
Aussi, on a $F$ appartient à $(\Delta)$, ce qui signifie que ses coordonnées vérifient l'équation de $(\Delta).$
Donc, en remplaçant $y$ par $0$ dans l'équation de $(\Delta)$, on obtient :
$\begin{array}{rcl} x-0+4=0&\Leftrightarrow&x+4=0\\\\&\Leftrightarrow&x=-4\end{array}$
Ainsi, $\boxed{x_{F}=-4}$
D'où, les coordonnées de $F$ sont données par :
$$\boxed{F\begin{pmatrix} -4\\0\end{pmatrix}}$$
4) Sans faire de calcul, donnons les coordonnées de $G$, point d'intersection de $(\mathcal{D})$ avec l'axe des ordonnées.
Les coordonnées de $G$ sont données par :
$$\boxed{G\begin{pmatrix} 0\\2\end{pmatrix}}$$
En effet, comme $G$ est le point d'intersection de $(\mathcal{D})$ avec l'axe des ordonnées alors, $G$ appartient à l'axe des ordonnées.
Ce qui signifie que son abscisse est égale à $0.$
Donc, $\boxed{x_{G}=0}$
Et par suite, son ordonnée est égale à l'ordonnée à l'origine de la droite $(\mathcal{D}).$
C'est-à-dire ; $\boxed{y_{G}=2}$
5) Représentons les droites $(\Delta)\ $ et $\ (\mathcal{D})$ puis plaçons les points $E\;,\ F\ $ et $\ G.$
Pour faire plus simple, on peut commencer par placer les points $E\;,\ F\ $ et $\ G.$
Ainsi, la droite passant par $E\ $ et $\ F$ est la droite $(\Delta)$ et celle passant par les points $E\ $ et $\ G$ représente la droite $(\mathcal{D}).$

Exercice 32
1) Plaçons dans un repère orthonormé les points $E\;,\ F\ $ et $\ G$ définis par leurs coordonnées :
$$E(-2\;;\ 2)\;;\ F(-3\;;\ -2)\;;\ G(6\;;\ 0)$$

2) Calculons le coefficient directeur de la droite $(EG).$
Soit $\overrightarrow{EG}$ un vecteur directeur de la droite $(EG).$
On a : $\overrightarrow{EG}\begin{pmatrix} 6-(-2)\\0-2\end{pmatrix}=\begin{pmatrix} 8\\-2\end{pmatrix}$
Or, on sait que si $\vec{u}\begin{pmatrix} m\\n\end{pmatrix}$ est un vecteur directeur d'une droite d'équation $y=ax+b$ avec $m\neq 0$ alors, le coefficient directeur de cette droite est :
$$a=\dfrac{n}{m}$$
Donc, en appliquant cette propriété à la droite $(EG)$ de vecteur directeur $\overrightarrow{EG}\begin{pmatrix} 8\\-2\end{pmatrix}$, on obtient :
$$\boxed{a=\dfrac{-2}{8}=\dfrac{-1}{4}}$$
3) Déterminons une équation de la droite $(EF).$
Soit $M\begin{pmatrix} x\\y\end{pmatrix}$ un point de la droite $(EF)$ alors, les vecteurs $\overrightarrow{EF}\ $ et $\ \overrightarrow{FM}$ sont colinéaires.
On a :
$\overrightarrow{EF}\begin{pmatrix} -3-(-2)\\-2-2\end{pmatrix}=\begin{pmatrix} -1\\-4\end{pmatrix}$
$\overrightarrow{FM}\begin{pmatrix} x-(-3)\\y-(-2)\end{pmatrix}=\begin{pmatrix} x+3\\y+2\end{pmatrix}$
Donc, en appliquant la propriété de colinéarité, on obtient :
$\begin{array}{rcl}\overrightarrow{EF}\ \text{ et }\ \overrightarrow{FM}\ \text{ sont colinéaires}&\Leftrightarrow&(x_{_{\overrightarrow{EF}}}\times y_{_{\overrightarrow{FM}}})-(x_{_{\overrightarrow{FM}}}\times y_{_{\overrightarrow{EF}}})=0\\\\&\Leftrightarrow&[-1\times(y+2)]-[(x+3)\times(-4)]=0\\ \\&\Leftrightarrow&-y-2+4x+12=0\\\\&\Leftrightarrow&-y+4x+10=0\\ \\&\Leftrightarrow&4x-y+10=0\end{array}$
D'où, une équation de la droite $(EG)$ est donnée par :
$$\boxed{(EG)\ :\ 4x-y+10=0}$$
4) Démontrons que les droites $(EF)\ $ et $\ (EG)$ sont perpendiculaires.
Soit $\overrightarrow{EF}\begin{pmatrix} -1\\-4\end{pmatrix}$ un vecteur directeur de la droite $(EF).$
Donc, le coefficient directeur $a'$ de la droite $(EF)$ est donné par :
$$\boxed{a'=\dfrac{-4}{-1}=4}$$
Alors, en faisant le produit des coefficients directeurs des droites $(EG)\ $ et $\ (EF)$, on trouve :
$\begin{array}{rcl} a\times a'&=&\dfrac{-1}{4}\times 4\\\\&=&\dfrac{-4}{4}\\\\&=&-1\end{array}$
Donc, $\boxed{a\times a'=-1}$
Ce qui signifie que les coefficients directeurs vérifient bien la condition d'orthogonalité.
Par conséquent, les droites $(EF)\ $ et $\ (EG)$ sont perpendiculaires.
5) Soit $M$ le milieu du segment $[FG].$
Calculons les coordonnées de $M.$
Les coordonnées de $M$ sont données par :
$$x_{M}=\dfrac{x_{F}+x_{G}}{2}\quad\text{et}\quad y_{M}=\dfrac{y_{F}+y_{G}}{2}$$
Par suite :
$x_{M}=\dfrac{-3+6}{2}=\dfrac{3}{2}$
$y_{M}=\dfrac{-2+0}{2}=\dfrac{-2}{2}=-1$
Ainsi,
$$\boxed{M\begin{pmatrix}\dfrac{3}{2}\\ \\-1\end{pmatrix}}$$
6) On désigne par $(\mathcal{C})$ le cercle circonscrit au triangle $EFG.$
a) Calculons les coordonnées de son centre $I$ et la valeur exacte de son rayon.
Comme les droite $(EF)\ $ et $\ (EG)$ sont perpendiculaires en $E$ alors, le triangle $EFG$ est rectangle en $E.$
Par suite, $[FG]$ est un diamètre pour le cercle $(\mathcal{C})$ circonscrit à ce triangle.
Donc, le milieu de $[FG]$ sera le centre de ce cercle.
Or, $M$ est milieu du segment $[FG].$
Par conséquent, $I=M$
D'où,
$$\boxed{I\begin{pmatrix}\dfrac{3}{2}\\ \\-1\end{pmatrix}}$$
Calculons la valeur exacte du rayon du cercle $(\mathcal{C}).$
$\begin{array}{rcl} IF&=&\sqrt{\left(-3-\dfrac{3}{2}\right)^{2}+(-2-(-1))^{2}}\\ \\&=&\sqrt{\left(\dfrac{-6}{2}-\dfrac{3}{2}\right)^{2}+(-2+1)^{2}}\\ \\&=&\sqrt{\left(\dfrac{-9}{2}\right)^{2}+(-1)^{2}}\\ \\&=&\sqrt{\dfrac{81}{4}+1}\\ \\&=&\sqrt{\dfrac{81}{4}+\dfrac{4}{4}}\\ \\&=&\sqrt{\dfrac{81+4}{4}}\\ \\&=&\sqrt{\dfrac{85}{4}}\\ \\&=&\dfrac{\sqrt{85}}{2}\end{array}$
Ainsi,
$$\boxed{\text{Rayon}=\dfrac{\sqrt{85}}{2}}$$
b) Déterminons l'équation de la droite $(\mathcal{D})$ perpendiculaire à $(IE)$ en $E.$
Soit $M\begin{pmatrix} x\\y\end{pmatrix}$ appartenant à la droite $(\mathcal{D})$
$(\mathcal{D})$ perpendiculaire à $(IE)$ en $E$ si, et seulement si, $\overrightarrow{IE}\ $ et $\ \overrightarrow{EM}$ sont orthogonaux.
Soit : $\overrightarrow{IE}\begin{pmatrix} -2-\dfrac{3}{2}\\ \\2-(-1)\end{pmatrix}=\begin{pmatrix} -\dfrac{7}{2}\\ \\3\end{pmatrix}\ $ et $\ \overrightarrow{EM}\begin{pmatrix} x-(-2)\\y-2\end{pmatrix}=\begin{pmatrix} x+2\\y-2\end{pmatrix}$
Alors, on a :
$\begin{array}{rcl}\overrightarrow{IE}\ \text{ et }\ \overrightarrow{EM}\ \text{ sont orthogonaux}&\Leftrightarrow&(x_{_{\overrightarrow{IE}}}\times x_{_{\overrightarrow{EM}}})+(y_{_{\overrightarrow{IE}}}\times y_{_{\overrightarrow{EM}}})=0\\\\&\Leftrightarrow&\left[\dfrac{-7}{2}\times(x+2)\right]+[3\times(y-2)]=0\\\\&\Leftrightarrow&\dfrac{-7}{2}x-7+3y-6=0\\\\&\Leftrightarrow&\dfrac{-7}{2}x+3y-13=0\end{array}$
D'où, une équation de la droite $(\mathcal{D})$ perpendiculaire à $(IE)$ en $E$ est donnée par :
$$\boxed{(\mathcal{D})\ :\ -\dfrac{7}{2}x+3y-13=0}$$
c) Calculons les valeurs exactes des longueurs $EF\ $ et $\ EG.$
Soit : $\overrightarrow{EF}\begin{pmatrix} -1\\-4\end{pmatrix}\ $ et $\ \overrightarrow{EG}\begin{pmatrix} 8\\-2\end{pmatrix}$ alors, on a :
$\begin{array}{rcl} EF&=&\sqrt{(-1)^{2}+(-4)^{2}}\\ \\&=&\sqrt{1+16}\\ \\&=&\sqrt{17}\end{array}$
Donc, $\boxed{EF=\sqrt{17}}$
$\begin{array}{rcl} EG&=&\sqrt{(8)^{2}+(-2)^{2}}\\ \\&=&\sqrt{64+4}\\ \\&=&\sqrt{68}\\ \\&=&2\sqrt{17}\end{array}$
Ainsi, $\boxed{EG=2\sqrt{17}}$
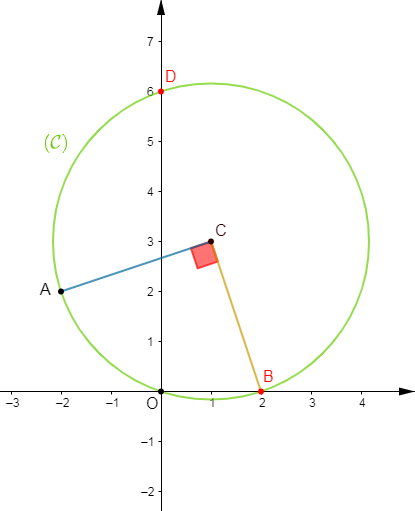
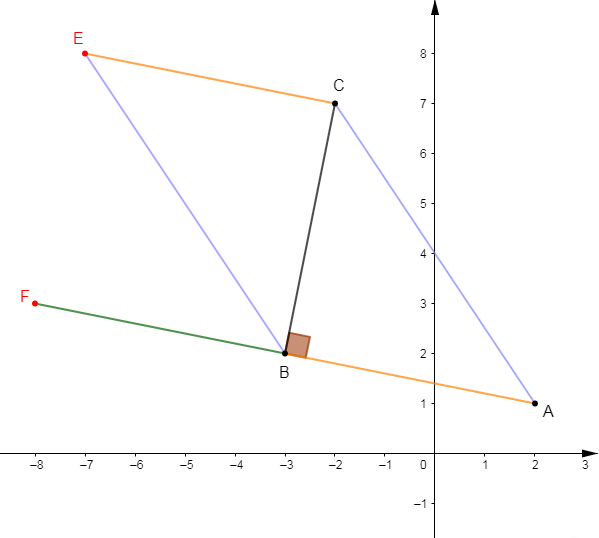
Exercice 33
1) Plaçons les points $A(4\;;\ 2)\ $ et $\ B(-2\;;\ -2)$ dans le plan muni d'un repère orthonormal.
2) Déterminons une équation de la droite $(OA).$
Une équation de la droite $(OA)$ peut se mettre sous la forme :
$$y=ax+b$$
avec $a$ son coefficient directeur et $b$ son ordonnée à l'origine.
On sait que la droite $(OA)$ passe par le point $O.$
Donc, les coordonnées de $O$ vérifient l'équation de $(OA).$
Ce qui se traduit par, $0=a\times 0+b\ \Rightarrow\ b=0$
En remplaçant $b$ par $0$, on obtient alors :
$$y=ax$$
Par ailleurs, comme $(OA)$ passe par le point $A$ alors, les coordonnées de $O$ vérifient l'équation de $(OA).$
C'est-à-dire ; $2=4a\ \Rightarrow\ a=\dfrac{2}{4}=\dfrac{1}{2}$
Ainsi, une équation réduite de $(OA)$ est donnée par :
$$\boxed{(OA)\ :\ y=\dfrac{1}{2}x}$$
3) On appelle $(\Delta)$ la médiatrice du segment $[OA].$
Montrons que $(\Delta)$ a pour équation $y=-2x+5.$
En effet, une équation réduite de $(\Delta)$ est de la forme :
$$y=a'x+b'$$
avec $a'$ son coefficient directeur et $b'$ son ordonnée à l'origine.
Comme $(\Delta)$ la médiatrice du segment $[OA]$ alors, $(\Delta)$ est perpendiculaire à la droite $(OA).$
Et donc, les coefficients directeurs $a\ $ et $\ a'$ de ces deux droites vérifient la condition d'orthogonalité.
Ce qui signifie alors :
$$\dfrac{1}{2}\times a'=-1\ \Rightarrow\ a'=-2$$
Ainsi, en remplaçant $a'$ par sa valeur $-2$, dans l'équation réduite, on obtient :
$$y=-2x+b'$$
Par ailleurs, comme $(\Delta)$ la médiatrice du segment $[OA]$ alors, $(\Delta)$ passe par le milieu du segment $[OA].$
Donc, les coordonnées de ce point vérifient l'équation de $(\Delta).$
Soit $I$ milieu de $[OA].$
Alors, on a :
$$x_{I}=\dfrac{4}{2}=2\ \text{ et }\ y_{I}=\dfrac{2}{2}=1$$
D'où,
$$\boxed{I\begin{pmatrix} 2\\1\end{pmatrix}}$$
Par suite, en remplaçant les coordonnées de $I$ dans l'équation réduite de $(\Delta)$, on obtient :
$\begin{array}{rcl} 1=-2\times 2+b'&\Rightarrow&b-4=1\\\\&\Rightarrow&b'=1+4\\\\&\Rightarrow&b'=5\end{array}$
Ainsi, en remplaçant $b'$ par sa valeur $5$, on obtient une équation réduite de $(\Delta)$ donnée par :
$$\boxed{(\Delta)\ :\ y=-2x+5}$$
4) Traçons la droite $(\delta_{1})$ d'équation $y=-x+4.$
Choisissons alors deux points $M\ $ et $\ N$ dont les coordonnées vérifient l'équation de la droite $(\delta_{1}).$
On a :
si $x=0$ alors, $y=0+4=4$
si $x=2$ alors, $y=-2+4=2$
Donc, plaçons les points $M\begin{pmatrix} 0\\4\end{pmatrix}\ $ et $\ N\begin{pmatrix} 2\\2\end{pmatrix}$ puis, traçons la droite passant par $M\ $ et $\ N.$ C'est la droite $(\delta_{1}).$
On appelle $(\delta_{2})$ la droite parallèle à $(\delta_{1})$ qui passe par le point $O.$
5) Déterminons une équation de $(\delta_{2}).$
Une équation réduite de $(\delta_{2})$ est de la forme :
$$y=a_{2}x+b_{2}$$
avec $a_{2}$ son coefficient directeur et $b_{2}$ son ordonnée à l'origine.
Comme $(\delta_{2})$ est parallèle à $(\delta_{1})$ alors, ces deux droites ont même coefficient directeur.
D'où, $\boxed{a_{2}=-1}$
Par ailleurs, on sait que $(\delta_{2})$ passe par le point $O$ donc, les coordonnées de ce point vérifient l'équation de $(\delta_{2}).$
C'est-à-dire ; $0=0+b$
Par suite, $\boxed{b=0}$
Ainsi, une équation de $(\delta_{2})$ est donnée par :
$$\boxed{(\delta_{2})\ :\ y=-x}$$
6) On appelle $P$ le point d'intersection des droites $(\Delta)\ $ et $\ (\delta_{1}).$
a) On a : $PO=PA$
En effet, comme $P$ est le point d'intersection des droites $(\Delta)\ $ et $\ (\delta_{1})$ alors, $P$ appartient à $(\Delta)$ médiatrice de $[OA].$
Or, on sait que : si un point appartient à la médiatrice d'un segment alors, ce point est équidistant des extrémités de ce segment.
Par conséquent, $P$ est équidistant des extrémités $O\ $ et $\ A$ du segment $[OA].$
D'où, $\boxed{PO=PA}$
b) Le triangle $OAP$ est isocèle en $P.$
En effet, d'après le résultat de la question $6)\;a)$, on a : $PO=PA$
Par conséquent, $OAP$ est un triangle isocèle en $P.$
c) Calculons les coordonnées du point $P.$
En effet, comme $P$ est le point d'intersection de $(\Delta)\ $ et $\ (\delta_{1})$ alors, ses coordonnées sont solutions du système d'équations formé par les équations respectives des droites $(\Delta)\ $ et $\ (\delta_{1}).$
Soit alors, à résoudre le système suivant :
$$\left\lbrace\begin{array}{rclr}y&=&-2x+5&\quad(1)\\\\y&=&-x+4&\quad(2)\end{array}\right.$$
Par comparaison des équations $(1)\ $ et $\ (2)$, on obtient :
$\begin{array}{rcl} \text{équation }(1)=\text{équation }(2)&\Leftrightarrow&-2x+5=-x+4\\\\&\Leftrightarrow&-2x+x=4-5\\\\&\Leftrightarrow&-x=-1\\\\&\Leftrightarrow&x=1\end{array}$
Donc, $\boxed{x=1}$
Ensuite, en remplaçant cette valeur de $x$ dans l'équation $(1)$, on trouve :
$\begin{array}{rcl} y&=&-2\times 1+5\\\\&=&-2+5\\\\&=&3\end{array}$
Donc, $\boxed{y=3}$
D'où, $S=\left\lbrace(1\;;\ 3)\right\rbrace$
Ainsi, les coordonnées de $P$ sont données par :
$$\boxed{P\begin{pmatrix} 1\\3\end{pmatrix}}$$
7) On appelle $E$ l'image du point $P$ par la translation de vecteur $\overrightarrow{OB}.$
Plaçons le point $E$ dans le repère.
Calculons les coordonnées de $E.$
Comme $E$ l'image du point $P$ par la translation de vecteur $\overrightarrow{OB}$ alors, cela signifie que :
$$\overrightarrow{PE}=\overrightarrow{OB}$$
Or, on sait que deux vecteurs sont égaux s'ils ont les mêmes coordonnées.
Soit alors :
$\overrightarrow{PE}\begin{pmatrix} x_{E}-1\\\\y_{E}-3\end{pmatrix}$
$\overrightarrow{OB}\begin{pmatrix} -2\\-2\end{pmatrix}$
Ainsi, on a :
$\begin{array}{rcl}\overrightarrow{PE}=\overrightarrow{OB}&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{E}-1&=&-2\\\\y_{E}-3&=&-2\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{E}&=&-2+1\\\\y_{E}&=&-2+3\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{E}&=&-1\\\\y_{E}&=&1\end{array}\right.\end{array}$
D'où,
$$\boxed{E\begin{pmatrix} -1\\1\end{pmatrix}}$$
Vérifions par le calcul que $E$ est un point de $(\delta_{2}).$
On sait que un point appartient à une droite si ses coordonnées vérifient l'équation de cette droite.
Donc, essayons de voir si les coordonnées de $E$ vérifient l'équation de $(\delta_{2}).$
En remplaçant les coordonnées de $E$ dans l'équation, on obtient : $1=-(-1).$ Ce qui est toujours vrai.
Donc, $\boxed{y_{E}=-x_{E}}$
Ce qui signifie que les coordonnées de $E$ vérifient bien l'équation de $(\delta_{2}).$
D'où, le point $E$ appartient à la droite $(\delta_{2}).$
8) Démontrons que $BE=AP.$
En effet, d'après la question $7)$, on a : $\overrightarrow{PE}=\overrightarrow{OB}.$
Ainsi, $PEBO$ est un parallélogramme.
Par suite, deux côtés opposés ont même longueur.
D'où, $PO=BE$
Or, d'après le résultat de la question $6)\;a)$, on a : $PO=PA$
Par conséquent, $\boxed{BE=PA}$

Exercice 34
Dans le plan muni d'un repère orthonormal, on donne les points ci-dessous :
$A(1\;;\ -1)\;;\ B(3\;;\ 1)\ $ et $\ C(-1\;;\ 3).$
1) Calculons $AB\;,\ AC\ $ et $\ BC$ puis, déduisons-en la nature du triangle $ABC.$
Soit : $\overrightarrow{AB}\begin{pmatrix} 3-1\\1-(-1)\end{pmatrix}=\begin{pmatrix} 2\\2\end{pmatrix}$ alors, on a :
$\begin{array}{rcl} AB&=&\sqrt{(2)^{2}+(2)^{2}}\\\\&=&\sqrt{4+4}\\\\&=&\sqrt{8}\\\\&=&\sqrt{4\times 2}\\\\&=&\sqrt{4}\times\sqrt{2}\\\\&=&2\sqrt{2}\end{array}$
Ainsi, $\boxed{AB=2\sqrt{2}}$
Soit : $\overrightarrow{AC}\begin{pmatrix} -1-1\\3-(-1)\end{pmatrix}=\begin{pmatrix} -2\\4\end{pmatrix}$ alors, on a :
$\begin{array}{rcl} AC&=&\sqrt{(-2)^{2}+(4)^{2}}\\\\&=&\sqrt{4+16}\\\\&=&\sqrt{20}\\\\&=&\sqrt{4\times 5}\\\\&=&\sqrt{4}\times\sqrt{5}\\\\&=&2\sqrt{5}\end{array}$
D'où, $\boxed{AC=2\sqrt{5}}$
Soit : $\overrightarrow{BC}\begin{pmatrix} -1-3\\3-1\end{pmatrix}=\begin{pmatrix} -4\\2\end{pmatrix}$ alors, on a :
$\begin{array}{rcl} BC&=&\sqrt{(-4)^{2}+(2)^{2}}\\\\&=&\sqrt{16+4}\\\\&=&\sqrt{20}\\\\&=&\sqrt{4\times 5}\\\\&=&\sqrt{4}\times\sqrt{5}\\\\&=&2\sqrt{5}\end{array}$
Ainsi, $\boxed{BC=2\sqrt{5}}$
On remarque alors que : $AC=BC$
Ce qui signifie que le triangle $ABC$ est isocèle en $C.$
2) Plaçons le point $D$ sur la demi-droite $[AC)$ tel que le triangle $ABD$ soit rectangle en $B.$
Pour cela, on trace la perpendiculaire à $(AB)$ passant par $B.$
Elle coupe alors $[AC)$ en $D.$
3) Traçons le cercle $(\mathcal{C})$ circonscrit au triangle $ABD.$
4) Démontrons que le point $C$ est le centre du cercle puis, calculons son rayon.
En effet, comme $ABC$ est isocèle en $C$ alors, la médiane issue de $C$ est aussi médiatrice du segment $[AB].$
Donc, $(CI)$ est perpendiculaire à $(AB).$
Or, deux droites perpendiculaires à une même droite sont parallèles.
Par conséquent, les droites $(CI)\ $ et $\ (BD)$ sont parallèles.
Ainsi, comme $I$ est milieu de $[AB]$ alors, d'après le théorème de la droite des milieux, $C$ est le milieu de $[AD].$
Par ailleurs, on sait que le triangle $ABD$ est rectangle en $B$ donc, le cercle $(\mathcal{C})$ circonscrit à ce triangle a pour centre le milieu de l'hypoténuse $[AD].$
D'où, $C$ est le centre du cercle $(\mathcal{C}).$
Calculons le rayon de ce cercle.
Comme $(\mathcal{C})$ de centre $C$ est circonscrit au triangle $ABD$ alors, son rayon $r$ est donné par :
$$r=CA$$
Ainsi, $\boxed{r=2\sqrt{5}}$
5) Calculons les coordonnées du point $D.$
Comme $C$ est milieu de $[AD]$ alors, cela signifie :
$$\overrightarrow{CD}=\overrightarrow{AC}$$
Or, on sait que deux vecteurs sont égaux s'ils ont les mêmes coordonnées.
Soit alors :
$\overrightarrow{CD}\begin{pmatrix} x_{D}-(-1)\\\\y_{D}-3\end{pmatrix}=\begin{pmatrix} x_{D}+1\\\\y_{D}-3\end{pmatrix}$
$\overrightarrow{AC}\begin{pmatrix} -2\\4\end{pmatrix}$
Ainsi, on a :
$\begin{array}{rcl}\overrightarrow{CD}=\overrightarrow{AC}&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{D}+1&=&-2\\\\y_{D}-3&=&4\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{D}&=&-2-1\\\\y_{D}&=&4+3\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{D}&=&-3\\\\y_{D}&=&7\end{array}\right.\end{array}$
D'où,
$$\boxed{D\begin{pmatrix} -3\\7\end{pmatrix}}$$
Construisons le point $K$ image de $A$ par la translation de vecteur $\overrightarrow{CB}$ puis, calculons les coordonnées de $K.$
En effet, comme $K$ est l'image de $A$ par la translation de vecteur $\overrightarrow{CB}$ alors, on a :
$$\overrightarrow{AK}=\overrightarrow{CB}$$
Or, on sait que deux vecteurs sont égaux s'ils ont les mêmes coordonnées.
Soit alors :
$\overrightarrow{AK}\begin{pmatrix} x_{K}-1\\\\y_{K}-(-1)\end{pmatrix}=\begin{pmatrix} x_{K}-1\\\\y_{K}+1\end{pmatrix}$
$\overrightarrow{CB}\begin{pmatrix} 3-(-1)\\1-3\end{pmatrix}=\begin{pmatrix} 4\\-2\end{pmatrix}$
Ainsi, on a :
$\begin{array}{rcl}\overrightarrow{AK}=\overrightarrow{CB}&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{K}-1&=&4\\\\y_{K}+1&=&-2\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{K}&=&4+1\\\\y_{K}&=&-2-1\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{K}&=&5\\\\y_{K}&=&-3\end{array}\right.\end{array}$
D'où,
$$\boxed{K\begin{pmatrix} 5\\-3\end{pmatrix}}$$
Donnons la nature du quadrilatère $CBKA.$
On a : $$\overrightarrow{AK}=\overrightarrow{CB}$$
Donc, $CBAK$ est parallélogramme.
De plus, les diagonales $(CK)\ $ et $\ (AB)$ sont perpendiculaires.
Par conséquent, $CBKA$ est un losange.
6) Traçons la hauteur $[BH]$ relative au côté $[AD]$ du triangle $ABD$, puis déterminons une équation cartésienne de la droite $(BH).$
C'est la droite $(BH)$ passant par $B$ et perpendiculaire au côté $[AD]$ en $H.$
Soit $N\begin{pmatrix} x\\y\end{pmatrix}$ un point appartenant à la droite $(BH).$
Alors, $(BH)$ est perpendiculaire à $(AD)$ si, et seulement si, $\overrightarrow{BN}\ $ et $\ \overrightarrow{AD}$ sont orthogonaux.
Soit alors :
$\ \overrightarrow{BN}\begin{pmatrix} x-3\\y-1\end{pmatrix}$
$\overrightarrow{AD}\begin{pmatrix} -3-1\\ 7-(-1)\end{pmatrix}=\begin{pmatrix} -4\\8\end{pmatrix}$
Ainsi, en utilisant la condition d'orthogonalité, on obtient :
$\begin{array}{rcl}\overrightarrow{BN}\ \text{ et }\ \overrightarrow{AD}\ \text{ sont orthogonaux}&\Leftrightarrow&(x_{_{\overrightarrow{BN}}}\times x_{_{\overrightarrow{AD}}})+(y_{_{\overrightarrow{BN}}}\times y_{_{\overrightarrow{AD}}})=0\\\\&\Leftrightarrow&\left[(x-3)\times(-4)\right]+[(y-1)\times 8]=0\\\\&\Leftrightarrow&-4x+12+8y-8=0\\\\&\Leftrightarrow&-4x+8y+4=0\end{array}$
D'où, une équation de la droite $(BH)$ est donnée par :
$$\boxed{(BH)\ :\ -4x+8y+4=0}$$
7) Le cercle $(\mathcal{C}')$ de centre $B$ passant par $C$, coupe le cercle $(\mathcal{C})$ en $M\ $ et $\ P.$
Justifions que la droite $(MP)$ est la médiatrice du segment $[BC]$, puis trouvons une équation générale de la droite $(MP).$
En effet, comme $(\mathcal{C}')$ est un cercle de centre $B$ passant par $C$ alors, son rayon est égal à $BC=2\sqrt{5}.$
Donc, les cercles $(\mathcal{C})\ $ et $\ (\mathcal{C}')$ ont le même rayon.
Par suite, $MC=MB\ $ et $\ PC=PB$
Ce qui signifie que les points $M\ $ et $\ P$ sont à égale distance des extrémités $B\ $ et $\ C$ du segment $[BC].$
Or, on sait que si un point est à égale distance des extrémités d'un segment alors, ce point appartient à la médiatrice de ce segment.
Donc, $M\ $ et $\ P$ appartiennent à la médiatrice du segment $[BC].$
D'où, la droite $(MP)$ est la médiatrice du segment $[BC].$
Trouvons une équation générale de la droite $(MP).$
En effet, on sait que $(MP)$ est la médiatrice du segment $[BC].$
Ce qui signifie que, la droite $(MP)$ est perpendiculaire à la droite $(BC)$ et passe par le milieu $J$ du segment $[BC]$ dont les coordonnées sont données par :
$$x_{J}=\dfrac{x_{B}+x_{C}}{2}\ \text{ et }\ y_{J}=\dfrac{y_{B}+y_{C}}{2}$$
Soit :
$\begin{array}{rcl}x_{J}&=&\dfrac{x_{B}+x_{C}}{2}\\\\&=&\dfrac{3-1}{2}\\\\&=&\dfrac{2}{2}\\\\&=&1\end{array}$
Donc, $\boxed{x_{J}=1}$
$\begin{array}{rcl}y_{J}&=&\dfrac{y_{B}+y_{C}}{2}\\\\&=&\dfrac{1+3}{2}\\\\&=&\dfrac{4}{2}\\\\&=&2\end{array}$
Alors, $\boxed{y_{J}=2}$
D'où,
$$\boxed{J\begin{pmatrix} 1\\2\end{pmatrix}}$$
Choisissons alors un point $R\begin{pmatrix} x\\y\end{pmatrix}$ appartenant à la droite $(MP).$
Alors, $(MP)$ est perpendiculaire à $(BC)$ si, et seulement si, les vecteurs $\overrightarrow{BC}\ $ et $\ \overrightarrow{JR}$ sont orthogonaux.
Soit alors :
$\overrightarrow{JR}\begin{pmatrix} x-1\\y-2\end{pmatrix}$
$\overrightarrow{BC}\begin{pmatrix} -4\\ 2\end{pmatrix}$
Ainsi, en utilisant la condition d'orthogonalité, on obtient :
$\begin{array}{rcl}\overrightarrow{BC}\ \text{ et }\ \overrightarrow{JR}\ \text{ sont orthogonaux}&\Leftrightarrow&(x_{_{\overrightarrow{BC}}}\times x_{_{\overrightarrow{JR}}})+(y_{_{\overrightarrow{BC}}}\times y_{_{\overrightarrow{JR}}})=0\\\\&\Leftrightarrow&\left[-4\times(x-1)\right]+[2\times(y-2)]=0\\\\&\Leftrightarrow&-4x+4+2y-4=0\\\\&\Leftrightarrow&-4x+2y=0\end{array}$
D'où, une équation de la droite $(MP)$ est donnée par :
$$\boxed{(MP)\ :\ -4x+2y=0}$$
8) Les droites $(MP)\ $ et $\ (BH)$ se coupent en $S.$
Calculons les coordonnées de $S.$
$S$ étant le point d'intersection de ces deux droites alors, ses coordonnées sont solutions du système d'équations formé par les équations respectives des droites $(MP)\ $ et $\ (BH).$
Soit alors, à résoudre le système suivant :
$$\left\lbrace\begin{array}{rclr} -4x+2y&=&0&\quad(1)\\\\-4x+8y+4&=&0&\quad(2)\end{array}\right.$$
En multipliant l'équation $(1)$ par $-1$, on obtient alors le système suivant :
$$\left\lbrace\begin{array}{rclr} 4x-2y&=&0&\quad(3)\\\\-4x+8y+4&=&0&\quad(2)\end{array}\right.$$
Par addition des équations $(3)\ $ et $\ (2)$, on trouve :
$\begin{array}{rcl} \text{équation }(3)+\text{équation }(2)&\Leftrightarrow&(4x-2y)+(-4x+8y+4)=0+0\\\\&\Leftrightarrow&4x-2y-4x+8y+4=0\\\\&\Leftrightarrow&6y+4=0\\\\&\Leftrightarrow&6y=-4\\\\&\Leftrightarrow&y=\dfrac{-4}{6}\\\\&\Leftrightarrow&y=-\dfrac{2\times 2}{2\times 3}\\\\&\Leftrightarrow&y=-\dfrac{2}{3}\end{array}$
Donc, $\boxed{y=-\dfrac{2}{3}}$
Ensuite, en remplaçant cette valeur de $y$ dans l'équation $(1)$, on trouve :
$\begin{array}{rcl} -4x+2\times\left(-\dfrac{2}{3}\right)=0&\Rightarrow&-4x-\dfrac{4}{3}=0\\\\&\Rightarrow&-4x=\dfrac{4}{3}\\\\&\Rightarrow&x=\dfrac{\dfrac{4}{3}}{-4}\\\\&\Rightarrow&x=\dfrac{4}{3}\times\dfrac{1}{-4}\\\\&\Rightarrow&x=\dfrac{1}{-3}\end{array}$
Donc, $\boxed{x=-\dfrac{1}{3}}$
D'où, l'ensemble des solutions est égal à : $\left\lbrace\left(-\dfrac{1}{3}\;;\ -\dfrac{2}{3}\right)\right\rbrace$
Ainsi, les coordonnées de $S$ sont données par :
$$\boxed{S\begin{pmatrix} -\dfrac{1}{3}\\\\-\dfrac{2}{3}\end{pmatrix}}$$
9) Détermine l'équation réduite de la droite $(\mathcal{T})$ tangente au cercle $(\mathcal{C}')$ en $K.$
Une équation réduite de la droite $(\mathcal{T})$ est de la forme :
$$y=ax+b$$
avec $a$ son coefficient directeur et $b$ son ordonnée à l'origine.
Comme $(\mathcal{T})$ tangente au cercle $(\mathcal{C}')$ en $K$ alors, la droite $(\mathcal{T})$ est perpendiculaire à la droite $(BK)$ au point $K.$
Ce qui signifie que leurs coefficients directeurs vérifient la condition d'orthogonalité.
Déterminons le coefficient directeur de la droite $(BK).$
Soit : $\overrightarrow{BK}$ un vecteur directeur de la droite $(BK).$
Alors, on a : $\overrightarrow{BK}\begin{pmatrix} 5-3\\-3-1\end{pmatrix}=\begin{pmatrix} 2\\-4\end{pmatrix}$
Par suite, le coefficient directeur de la droite $(BK)$ est égal à : $\dfrac{-4}{2}=-2$
Donc, en appliquant la condition d'orthogonalité, on trouve :
$$-2\times a=-1\ \Rightarrow\ a=\dfrac{-1}{-2}=\dfrac{1}{2}$$
D'où, $\boxed{a=\dfrac{1}{2}}$
Ainsi, en remplaçant le coefficient $a$ par sa valeur $\dfrac{1}{2}$, l'équation réduite de $(\mathcal{T})$ devient :
$$y=\dfrac{1}{2}x+b$$
Par ailleurs, on sait que la droite $(\mathcal{T})$ passe par $K$ donc, les coordonnées de ce point vérifient l'équation de $(\mathcal{T}).$
Ainsi, on a :
$\begin{array}{rcl} -3=\dfrac{1}{2}\times 5+b&\Rightarrow&b+\dfrac{5}{2}=-3\\\\&\Rightarrow&b=-3-\dfrac{5}{2}\\\\&\Rightarrow&b=-\dfrac{6}{2}-\dfrac{5}{2}\\\\&\Rightarrow&b=-\dfrac{11}{2}\end{array}$
Donc, $\boxed{b=-\dfrac{11}{2}}$
D'où, une équation réduite de la droite $(\mathcal{T})$ tangente au cercle $(\mathcal{C}')$ en $K$ est donnée par :
$$\boxed{(\mathcal{T})\ :\ y=\dfrac{1}{2}x-\dfrac{11}{2}}$$
10) Détermine l'équation réduite de la droite $(\Delta)$, parallèle à la droite $(MP)$, passant par $C.$
Une équation réduite de la droite $(\Delta)$ est de la forme :
$$y=a'x+b'$$
avec $a'$ son coefficient directeur et $b'$ son ordonnée à l'origine.
Comme $(\Delta)$ est parallèle à $(MP)$ alors, les deux droites ont même coefficient directeur.
Or, $(MP)$ est d'équation : $-4x+2y=0$
Donc, $\vec{u}\begin{pmatrix} -2\\-4\end{pmatrix}$ est un vecteur directeur de $(MP).$
Par suite, son coefficient directeur est égal à : $\dfrac{-4}{-2}=2$
Ainsi, le coefficient directeur de $(\Delta)$ est égal à $2.$
C'est-à-dire ; $\boxed{a'=2}$
Ensuite, en remplaçant le coefficient $a'$ par sa valeur $2$, l'équation réduite de $(\Delta)$ devient :
$$y=2x+b$$
Par ailleurs, on sait que $(\Delta)$ passe par $C$ donc, les coordonnées de ce point vérifient l'équation de $(\Delta).$
Ainsi, on a :
$\begin{array}{rcl} 3=2\times(-1)+b'&\Rightarrow&b'-2=3\\\\&\Rightarrow&b'=3+2\\\\&\Rightarrow&b'=5\end{array}$
Donc, $\boxed{b'=5}$
D'où, une équation réduite de la droite $(\Delta)$, parallèle à la droite $(MP)$, passant par $C$ est donnée par :
$$\boxed{(\Delta)\ :\ y=2x+5}$$

Exercice 35
On donne les points : $A(0\;;\ 4)\;;\ B(4\;;\ 0)\ $ et $\ C(-3\;;\ 0).$
1) Calculons les coordonnées du centre de gravité $G$ du triangle $ABC.$
En effet, le centre de gravité $G$ du triangle $ABC$ est le point de rencontre des médianes de ce triangle.
Soit $J$ milieu de $[AC]\ $ et $\ K$ milieu de $[AB].$
Donc, les droites $(BJ\ $ et $\ (CK)$ sont deux médianes du triangles $ABC.$
Déterminons d'abord les coordonnées de $J\ $ et $\ K$
$-\ $ les coordonnées de $J$ sont données par :
$\begin{array}{rcl}x_{J}&=&\dfrac{x_{A}+x_{C}}{2}\\\\&=&\dfrac{0-3}{2}\\\\&=&\dfrac{-3}{2}\end{array}$
Donc, $\boxed{x_{J}=-\dfrac{3}{2}}$
$\begin{array}{rcl}y_{J}&=&\dfrac{y_{A}+y_{C}}{2}\\\\&=&\dfrac{4+0}{2}\\\\&=&\dfrac{4}{2}\\\\&=&2\end{array}$
Donc, $\boxed{y_{J}=2}$
Ainsi,
$$\boxed{J\begin{pmatrix} -\dfrac{3}{2}\\\\2\end{pmatrix}}$$
$-\ $ les coordonnées de $K$ sont données par :
$\begin{array}{rcl}x_{K}&=&\dfrac{x_{A}+x_{B}}{2}\\\\&=&\dfrac{0+4}{2}\\\\&=&\dfrac{4}{2}\\\\&=&2\end{array}$
Donc, $\boxed{x_{K}=2}$
$\begin{array}{rcl}y_{K}&=&\dfrac{y_{A}+y_{B}}{2}\\\\&=&\dfrac{4+0}{2}\\\\&=&\dfrac{4}{2}\\\\&=&2\end{array}$
Donc, $\boxed{y_{K}=2}$
D'où,
$$\boxed{K\begin{pmatrix} 2\\2\end{pmatrix}}$$
Déterminons ensuite les équations des médianes $(BJ)\ $ et $\ (CK).$
$-\ $ équation de $(BJ)$
En effet, la médiane $(BJ)$ est la droite passant par les points $B\ $ et $\ J.$
Choisissons $M\begin{pmatrix} x\\y\end{pmatrix}\in(BJ)$ alors, $\overrightarrow{BM}\ $ et $\ \overrightarrow{BJ}$ sont colinéaires.
Soit :
$\overrightarrow{BM}\begin{pmatrix} x-4\\y-0\end{pmatrix}=\begin{pmatrix} x-4\\y\end{pmatrix}$
$\overrightarrow{BJ}\begin{pmatrix} -\dfrac{3}{2}-4\\\\2-0\end{pmatrix}=\begin{pmatrix} -\dfrac{3}{2}-\dfrac{8}{2}\\\\2\end{pmatrix}=\begin{pmatrix} -\dfrac{11}{2}\\\\2\end{pmatrix}$
Ainsi, en appliquant la condition de colinéarité, on obtient :
$\begin{array}{rcl}\overrightarrow{BM}\ \text{ et }\ \overrightarrow{BJ}\ \text{ sont colinéaires}&\Leftrightarrow&(x_{_{\overrightarrow{BM}}}\times y_{_{\overrightarrow{BJ}}})-(x_{_{\overrightarrow{BJ}}}\times y_{_{\overrightarrow{BM}}})=0\\\\&\Leftrightarrow&\left[(x-4)\times 2\right]-\left[-\dfrac{11}{2}\times y\right]=0\\\\&\Leftrightarrow&2x-8+\dfrac{11}{2}y=0\\\\&\Leftrightarrow&2x+\dfrac{11}{2}y-8=0\end{array}$
D'où, une équation de la droite $(BJ)$ est donnée par :
$$\boxed{(BJ)\ :\ 2x+\dfrac{11}{2}y-8=0}$$
$-\ $ équation de $(CK)$
La médiane $(CK)$ est la droite passant par les points $C\ $ et $\ K.$
Choisissons un point $M\begin{pmatrix} x\\y\end{pmatrix}$ appartenant à la droite $(CK)$ alors, les vecteurs $\overrightarrow{CM}\ $ et $\ \overrightarrow{CK}$ sont colinéaires.
Soit :
$\overrightarrow{CM}\begin{pmatrix} x-(-3)\\y-0\end{pmatrix}=\begin{pmatrix} x+3\\y\end{pmatrix}$
$\overrightarrow{CK}\begin{pmatrix} 2-(-3)\\2-0\end{pmatrix}=\begin{pmatrix} 5\\2\end{pmatrix}$
Ainsi, en appliquant la condition de colinéarité, on obtient :
$\begin{array}{rcl}\overrightarrow{CM}\ \text{ et }\ \overrightarrow{CK}\ \text{ sont colinéaires}&\Leftrightarrow&(x_{_{\overrightarrow{CM}}}\times y_{_{\overrightarrow{CK}}})-(x_{_{\overrightarrow{CK}}}\times y_{_{\overrightarrow{CM}}})=0\\\\&\Leftrightarrow&\left[(x+3)\times 2\right]-\left[5\times y\right]=0\\\\&\Leftrightarrow&2x+6-5y=0\\\\&\Leftrightarrow&2x-5y+6=0\end{array}$
D'où, une équation de la droite $(CK)$ est donnée par :
$$\boxed{(CK)\ :\ 2x-5y+6=0}$$
Calculons enfin les coordonnées du centre de gravité $G$ du triangle $ABC.$
En effet, $G$ est le point de rencontre des droites $(BJ)\ $ et $\ (CK).$
Donc, ses coordonnées sont solutions du système d'équations formé par les équations respectives de ces droites.
Soit alors, à résoudre le système suivant :
$$\left\lbrace\begin{array}{rclr} 2x+\dfrac{11}{2}y-8&=&0&\quad(1)\\\\2x-5y+6&=&0&\quad(2)\end{array}\right.$$
En multipliant l'équation $(2)$ par $-1$, on obtient alors le système suivant :
$$\left\lbrace\begin{array}{rclr} 2x+\dfrac{11}{2}y-8&=&0&\quad(1)\\\\-2x+5y-6&=&0&\quad(3)\end{array}\right.$$
Par addition des équations $(1)\ $ et $\ (3)$, on trouve :
$\begin{array}{rcl} \text{équation }(1)+\text{équation }(3)&\Leftrightarrow&\left(2x+\dfrac{11}{2}y-8\right)+(-2x+5y-6)=0+0\\\\&\Leftrightarrow&2x+\dfrac{11}{2}y-8-2x+5y-6=0\\\\&\Leftrightarrow&\dfrac{11}{2}y+\dfrac{10}{2}y-14=0\\\\&\Leftrightarrow&\dfrac{21}{2}y=14\\\\&\Leftrightarrow&y=\dfrac{14}{\dfrac{21}{2}}\\\\&\Leftrightarrow&y=\dfrac{14}{1}\times\dfrac{2}{21}\\\\&\Leftrightarrow&y=\dfrac{28}{21}\\\\&\Leftrightarrow&y=\dfrac{4}{3}\end{array}$
Donc, $\boxed{y=\dfrac{4}{3}}$
Ensuite, en remplaçant cette valeur de $y$ dans l'équation $(2)$, on trouve :
$\begin{array}{rcl} 2x-5\times\left(\dfrac{4}{3}\right)+6=0&\Rightarrow&2x-\dfrac{20}{3}+6=0\\\\&\Rightarrow&2x-\dfrac{20}{3}+\dfrac{18}{3}=0\\\\&\Rightarrow&2x-\dfrac{2}{3}=0\\\\&\Rightarrow&2x=\dfrac{2}{3}\\\\&\Rightarrow&x=\dfrac{\dfrac{2}{3}}{2}\\\\&\Rightarrow&x=\dfrac{2}{3}\times\dfrac{1}{2}\\\\&\Rightarrow&x=\dfrac{1}{3}\end{array}$
Donc, $\boxed{x=\dfrac{1}{3}}$
D'où, $S=\left\lbrace\left(\dfrac{1}{3}\;;\ \dfrac{4}{3}\right)\right\rbrace$
Ainsi, les coordonnées de $G$ sont données par :
$$\boxed{G\begin{pmatrix} \dfrac{1}{3}\\\\\dfrac{4}{3}\end{pmatrix}}$$
2) Calculons les coordonnées de l'orthocentre $H$ du triangle $ABC.$
En effet, l'orthocentre $H$ du triangle $ABC$ est le point de rencontre des hauteurs de ce triangle.
Soit : $(\Delta_{1})$ la hauteur issue de $B\ $ et $\ (\Delta_{2})$ la hauteur issue de $C.$
Déterminons alors les équations des droites $(\Delta_{1})\ $ et $\ (\Delta_{2}).$
$-\ $ équation de $(\Delta_{1})$
$(\Delta_{1})$ est la droite perpendiculaire à la droite $(AC)$ et passant par le point $B.$
Soit $M\begin{pmatrix} x\\y\end{pmatrix}$ un point appartenant à la droite $(\Delta_{1})$
Alors, $(\Delta_{1})$ est perpendiculaire à $(AC)$ si, et seulement si, les vecteurs $\overrightarrow{BM}\ $ et $\ \overrightarrow{AC}$ sont orthogonaux.
Soit alors :
$\overrightarrow{BM}\begin{pmatrix} x-4\\y-0\end{pmatrix}=\begin{pmatrix} x-4\\y\end{pmatrix}$
$\overrightarrow{AC}\begin{pmatrix} -3-0\\ 0-4\end{pmatrix}=\begin{pmatrix} -3\\-4\end{pmatrix}$
Ainsi, en utilisant la condition d'orthogonalité, on obtient :
$\begin{array}{rcl}\overrightarrow{BM}\ \text{ et }\ \overrightarrow{AC}\ \text{ sont orthogonaux}&\Leftrightarrow&(x_{_{\overrightarrow{BM}}}\times x_{_{\overrightarrow{AC}}})+(y_{_{\overrightarrow{BM}}}\times y_{_{\overrightarrow{AC}}})=0\\\\&\Leftrightarrow&\left[(x-4)\times(-3)\right]+[y\times(-4)]=0\\\\&\Leftrightarrow&-3x+12-4y=0\\\\&\Leftrightarrow&-3x-4y+12=0\end{array}$
D'où, une équation de la droite $(\Delta_{1})$ est donnée par :
$$\boxed{(\Delta_{1})\ :\ -3x-4y+12=0}$$
$-\ $ équation de $(\Delta_{2})$
$(\Delta_{2})$ est la droite perpendiculaire à la droite $(AB)$ et passant par le point $C.$
Considérons un point $M\begin{pmatrix} x\\y\end{pmatrix}$ appartenant à la droite $(\Delta_{2})$
Alors, $(\Delta_{2})$ est perpendiculaire à $(AB)$ si, et seulement si, les vecteurs $\overrightarrow{CM}\ $ et $\ \overrightarrow{AB}$ sont orthogonaux.
Soit alors :
$\overrightarrow{CM}\begin{pmatrix} x-(-3)\\y-0\end{pmatrix}=\begin{pmatrix} x+3\\y\end{pmatrix}$
$\overrightarrow{AB}\begin{pmatrix} 4-0\\ 0-4\end{pmatrix}=\begin{pmatrix} 4\\-4\end{pmatrix}$
Ainsi, en utilisant la condition d'orthogonalité, on obtient :
$\begin{array}{rcl}\overrightarrow{CM}\ \text{ et }\ \overrightarrow{AB}\ \text{ sont orthogonaux}&\Leftrightarrow&(x_{_{\overrightarrow{CM}}}\times x_{_{\overrightarrow{AB}}})+(y_{_{\overrightarrow{CM}}}\times y_{_{\overrightarrow{AB}}})=0\\\\&\Leftrightarrow&\left[(x+3)\times 4\right]+[y\times(-4)]=0\\\\&\Leftrightarrow&4x+12-4y=0\\\\&\Leftrightarrow&4x-4y+12=0\end{array}$
D'où, une équation de la droite $(\Delta_{2})$ est donnée par :
$$\boxed{(\Delta_{2})\ :\ 4x-4y+12=0}$$
Calculons ensuite les coordonnées de l'orthocentre $H$ du triangle $ABC.$
En effet, $H$ est le point de rencontre des droites $(\Delta_{1})\ $ et $\ (\Delta_{2}).$
Donc, ses coordonnées sont solutions du système d'équations formé par les équations respectives de ces droites.
Soit alors, à résoudre le système suivant :
$$\left\lbrace\begin{array}{rclr} -3x-4y+12&=&0&\quad(1)\\\\4x-4y+12&=&0&\quad(2)\end{array}\right.$$
En multipliant l'équation $(1)$ par $-1$, on obtient alors le système suivant :
$$\left\lbrace\begin{array}{rclr} 3x+4y-12&=&0&\quad(3)\\\\4x-4y+12&=&0&\quad(2)\end{array}\right.$$
Par addition des équations $(3)\ $ et $\ (2)$, on trouve :
$\begin{array}{rcl} \text{équation }(3)+\text{équation }(2)&\Leftrightarrow&\left(3x+4y-12\right)+(4x-4y+12)=0+0\\\\&\Leftrightarrow&3x+4y-12+4x-4y+12=0\\\\&\Leftrightarrow&7x=0\\\\&\Leftrightarrow&x=\dfrac{0}{7}\\\\&\Leftrightarrow&x=0\end{array}$
Donc, $\boxed{x=0}$
Ensuite, en remplaçant cette valeur de $x$ dans l'équation $(2)$, on trouve :
$\begin{array}{rcl} 4\times 0-4y+12=0&\Rightarrow&-4y+12=0\\\\&\Rightarrow&-4y=-12\\\\&\Rightarrow&y=\dfrac{-12}{-4}\\\\&\Rightarrow&y=3\end{array}$
Donc, $\boxed{y=3}$
D'où, $S=\left\lbrace\left(0\;;\ 3\right)\right\rbrace$
Par conséquent, les coordonnées de $H$ sont données par :
$$\boxed{H\begin{pmatrix} 0\\3\end{pmatrix}}$$
3) Calcule les coordonnées de $\Omega$ centre du cercle circonscrit au triangle $ABC.$
En effet, le centre $\Omega$ du cercle circonscrit au triangle $ABC$ est le point de rencontre des médiatrices de ce triangle.
Soit : $(d_{1})$ la médiatrice du segment $[AC]\ $ et $\ (d_{2})$ la médiatrice du segment $[AB].$
Déterminons alors les équations des droites $(d_{1})\ $ et $\ (d_{2}).$
$-\ $ équation de $(d_{1})$
$(d_{1})$ est la droite perpendiculaire à la droite $(AC)$ et passant par le point $J$ milieu de $[AC].$
Soit $M\begin{pmatrix} x\\y\end{pmatrix}$ un point appartenant à la droite $(d_{1})$
Alors, $(d_{1})$ est perpendiculaire à $(AC)$ si, et seulement si, les vecteurs $\overrightarrow{JM}\ $ et $\ \overrightarrow{AC}$ sont orthogonaux.
Soit alors :
$\overrightarrow{JM}\begin{pmatrix} x-\left(-\dfrac{3}{2}\right)\\\\y-2\end{pmatrix}=\begin{pmatrix} x+\dfrac{3}{2}\\\\y-2\end{pmatrix}$
$\overrightarrow{AC}\begin{pmatrix} -3\\-4\end{pmatrix}$
Ainsi, en utilisant la condition d'orthogonalité, on obtient :
$\begin{array}{rcl}\overrightarrow{JM}\ \text{ et }\ \overrightarrow{AC}\ \text{ sont orthogonaux}&\Leftrightarrow&(x_{_{\overrightarrow{JM}}}\times x_{_{\overrightarrow{AC}}})+(y_{_{\overrightarrow{JM}}}\times y_{_{\overrightarrow{AC}}})=0\\\\&\Leftrightarrow&\left[\left(x+\dfrac{3}{2}\right)\times(-3)\right]+[(y-2)\times(-4)]=0\\\\&\Leftrightarrow&-3x-\dfrac{9}{2}-4y+8=0\\\\&\Leftrightarrow&-3x-4y-\dfrac{9}{2}+\dfrac{16}{2}=0\\\\&\Leftrightarrow&-3x-4y+\dfrac{7}{2}=0\end{array}$
D'où, une équation de la droite $(d_{1})$ est donnée par :
$$\boxed{(d_{1})\ :\ -3x-4y+\dfrac{7}{2}=0}$$
$-\ $ équation de $(d_{2})$
$(d_{2})$ est la droite perpendiculaire à la droite $(AB)$ et passant par le point $K$ milieu de $[AB].$
Considérons un point $M\begin{pmatrix} x\\y\end{pmatrix}$ appartenant à la droite $(d_{2})$
Alors, $(d_{2})$ est perpendiculaire à $(AB)$ si, et seulement si, les vecteurs $\overrightarrow{KM}\ $ et $\ \overrightarrow{AB}$ sont orthogonaux.
Soit alors :
$\overrightarrow{KM}\begin{pmatrix} x-2\\y-2\end{pmatrix}$
$\overrightarrow{AB}\begin{pmatrix} 4\\-4\end{pmatrix}$
Ainsi, en utilisant la condition d'orthogonalité, on obtient :
$\begin{array}{rcl}\overrightarrow{KM}\ \text{ et }\ \overrightarrow{AB}\ \text{ sont orthogonaux}&\Leftrightarrow&(x_{_{\overrightarrow{KM}}}\times x_{_{\overrightarrow{AB}}})+(y_{_{\overrightarrow{KM}}}\times y_{_{\overrightarrow{AB}}})=0\\\\&\Leftrightarrow&\left[(x-2)\times 4\right]+[(y-2)\times(-4)]=0\\\\&\Leftrightarrow&4x-8-4y+8=0\\\\&\Leftrightarrow&4x-4y=0\end{array}$
D'où, une équation de la droite $(d_{2})$ est donnée par :
$$\boxed{(d_{2})\ :\ 4x-4y=0}$$
Calculons ensuite les coordonnées de $\Omega$ centre du cercle circonscrit au triangle $ABC.$
En effet, $\Omega$ est le point de rencontre des droites $(d_{1})\ $ et $\ (d_{2}).$
Donc, ses coordonnées sont solutions du système d'équations formé par les équations respectives de ces droites.
Soit alors, à résoudre le système suivant :
$$\left\lbrace\begin{array}{rclr} -3x-4y+\dfrac{7}{2}&=&0&\quad(1)\\\\4x-4y&=&0&\quad(2)\end{array}\right.$$
En multipliant l'équation $(1)$ par $-1$, on obtient alors le système suivant :
$$\left\lbrace\begin{array}{rclr} 3x+4y-\dfrac{7}{2}&=&0&\quad(3)\\\\4x-4y&=&0&\quad(2)\end{array}\right.$$
Par addition des équations $(3)\ $ et $\ (2)$, on trouve :
$\begin{array}{rcl} \text{équation }(3)+\text{équation }(2)&\Leftrightarrow&\left(3x+4y-\dfrac{7}{2}\right)+(4x-4y)=0+0\\\\&\Leftrightarrow&3x+4y-\dfrac{7}{2}+4x-4y=0\\\\&\Leftrightarrow&7x-\dfrac{7}{2}=0\\\\&\Leftrightarrow&7x=\dfrac{7}{2}\\\\&\Leftrightarrow&x=\dfrac{\dfrac{7}{2}}{7}\\\\&\Leftrightarrow&x=\dfrac{7}{2}\times\dfrac{1}{7}\\\\&\Leftrightarrow&x=\dfrac{1}{2}\end{array}$
Donc, $\boxed{x=\dfrac{1}{2}}$
Ensuite, en remplaçant cette valeur de $x$ dans l'équation $(2)$, on trouve :
$\begin{array}{rcl} 4\times\dfrac{1}{2}-4y=0&\Rightarrow&\dfrac{4}{2}-4y=0\\\\&\Rightarrow&2-4y=\\\\&\Rightarrow&-4y=-2\\\\&\Rightarrow&y=\dfrac{-2}{-4}\\\\&\Rightarrow&y=\dfrac{1}{2}\end{array}$
Donc, $\boxed{y=\dfrac{1}{2}}$
D'où, $S=\left\lbrace\left(\dfrac{1}{2}\;;\ \dfrac{1}{2}\right)\right\rbrace$
Ainsi, les coordonnées de $\Omega$ sont données par :
$$\boxed{\Omega\begin{pmatrix} \dfrac{1}{2}\\\\\dfrac{1}{2}\end{pmatrix}}$$
4) Vérifions que les points $\Omega\;,\ G\ $ et $\ H$ sont alignés.
Pour cela, il suffit de vérifier que les vecteurs $\overrightarrow{G\Omega}\ $ et $\ \overrightarrow{G\Omega}$ sont colinéaires.
Soit :
$\overrightarrow{G\Omega}\begin{pmatrix} \dfrac{1}{2}-\dfrac{1}{3}\\\\\dfrac{1}{2}-\dfrac{4}{3}\end{pmatrix}=\begin{pmatrix} \dfrac{3}{6}-\dfrac{2}{6}\\\\\dfrac{3}{6}-\dfrac{8}{6}\end{pmatrix}=\begin{pmatrix} \dfrac{1}{6}\\\\-\dfrac{5}{6}\end{pmatrix}$
$\overrightarrow{H\Omega}\begin{pmatrix} \dfrac{1}{2}-0\\\\\dfrac{1}{2}-3\end{pmatrix}=\begin{pmatrix} \dfrac{1}{2}\\\\\dfrac{1}{2}-\dfrac{6}{2}\end{pmatrix}=\begin{pmatrix} \dfrac{1}{2}\\\\-\dfrac{5}{2}\end{pmatrix}$
Alors, on a :
$\begin{array}{rcl} \dfrac{1}{6}\times\left(-\dfrac{5}{2}\right)-\dfrac{1}{2}\times\left(-\dfrac{5}{6}\right)&=&-\dfrac{5}{12}+\dfrac{5}{12}\\\\&=&0\end{array}$
On constate que les coordonnées des vecteurs $\overrightarrow{G\Omega}\ $ et $\ \overrightarrow{G\Omega}$ vérifient la condition de colinéarité.
Ce qui signifie que les vecteurs $\overrightarrow{G\Omega}\ $ et $\ \overrightarrow{G\Omega}$ sont colinéaires.
D'où, les points $\Omega\;,\ G\ $ et $\ H$ sont alignés.

Exercice 37
Dans le plan muni d'un repère orthonormal, on donne les points $A(-2\;;\ 2)\;;\ B(x\;;\ 0)\ $ et $\ C(1\;;\ 3).$
1) Déterminons la valeur de $x$ pour laquelle la droite $(CB)$ est orthogonale à la droite $(CA).$
On a : la droite $(CB)$ est orthogonale à la droite $(CA)$ si, et seulement si, les vecteurs $\overrightarrow{CB}\ $ et $\ \overrightarrow{CA}$ sont orthogonaux.
Soit :
$\overrightarrow{CB}\begin{pmatrix} x-1\\0-3\end{pmatrix}=\begin{pmatrix} x-1\\-3\end{pmatrix}$
$\overrightarrow{CA}\begin{pmatrix} -2-1\\2-3\end{pmatrix}=\begin{pmatrix} -3\\-1\end{pmatrix}$
Alors, en appliquant la condition de d'orthogonalité, on obtient :
$\begin{array}{rcl}\overrightarrow{CB}\ \text{ et }\ \overrightarrow{CA}\ \text{ sont orthogonaux}&\Leftrightarrow&[(x-1)\times(-3)]+\left[(-3)\times(-1)\right]=0\\\\&\Leftrightarrow&-3x+3+3=0\\\\&\Leftrightarrow&-3x+6=0\\\\&\Leftrightarrow&-3x=-6\\\\&\Leftrightarrow&x=\dfrac{-6}{-3}\\\\&\Leftrightarrow&x=2\end{array}$
D'où, $\boxed{x=2}$
Ainsi,
$$\boxed{B\begin{pmatrix} 2\\0\end{pmatrix}}$$
Montrons alors que $C$ appartient à la médiatrice de $[AB].$
En effet, on sait que si un point est équidistant des extrémités d'un segment alors, ce point appartient à la médiatrice de ce segment.
Donc, calculons les longueurs $CA\ $ et $\ CB$
Soit : $\overrightarrow{CA}\begin{pmatrix} -3\\-1\end{pmatrix}$ alors, on a :
$\begin{array}{rcl} CA&=&\sqrt{(-1)^{2}+(-3)^{2}}\\\\&=&\sqrt{1+9}\\\\&=&\sqrt{10}\end{array}$
Donc, $\boxed{CA=\sqrt{10}}$
Soit : $\overrightarrow{CB}\begin{pmatrix} 2-1\\0-3\end{pmatrix}=\begin{pmatrix} 1\\-3\end{pmatrix}$ alors, on a :
$\begin{array}{rcl} CB&=&\sqrt{(1)^{2}+(-3)^{2}}\\\\&=&\sqrt{1+9}\\\\&=&\sqrt{10}\end{array}$
Donc, $\boxed{CB=\sqrt{10}}$
On remarque alors que $CA=CB$
Par conséquent, le point $C$ appartient à la médiatrice du segment $[AB].$
2) On considère le cercle $(\mathcal{C})$ de centre $C$ passant par $A.$
Donc, ce cercle a pour rayon $r=CA=\sqrt{10}$
Montrons qu'il passe par $B\ $ et $\ O.$
En effet, un cercle passe par un point si la distance entre ce point et le rayon de ce cercle est égale au rayon.
Or, d'après le résultat de la question $1)$, on a : $CB=\sqrt{10}=r$
Par conséquent, le cercle $(\mathcal{C})$ passe par $B.$
En calculant la longueur $CO$ on trouve :
$\begin{array}{rcl} CO&=&\sqrt{(0-1)^{2}+(0-3)^{2}}\\\\&=&\sqrt{(-1)^{2}+(-3)^{2}}\\\\&=&\sqrt{1+9}\\\\&=&\sqrt{10}\end{array}$
Donc, $\boxed{CO=\sqrt{10}}$
Ce qui signifie que la distance entre le centre du cercle $(\mathcal{C})$ et le pont $O$ est égale au rayon de ce cercle.
D'où, $O$ appartient au cercle $(\mathcal{C}).$
3) Déterminons les points d'intersection de $(\mathcal{C})$ avec les axes du repère.
Le cercle $(\mathcal{C})$ coupe l'axe des abscisses au point $B$ et l'axe des ordonnées au point $D.$
Déterminons alors les coordonnées de $D.$
Comme $D$ est sur l'axe des ordonnées alors, on a : $\boxed{x_{D}=0}$
Par ailleurs, le cercle $(\mathcal{C})$ passe par $D$ donc,
$$CD=r$$
Soit : $\overrightarrow{CD}\begin{pmatrix} 0-1\\\\y_{D}-3\end{pmatrix}=\begin{pmatrix} -1\\\\y_{D}-3\end{pmatrix}.$
Alors, $CD=\sqrt{(-1)^{2}+(y_{D}-3)^{2}}=\sqrt{1+(y_{D}-3)^{2}}$
Ainsi, on a :
$\begin{array}{rcl}CD=r&\Leftrightarrow&\sqrt{1+(y_{D}-3)^{2}}=\sqrt{10}\\\\&\Leftrightarrow&\left(\sqrt{1+(y_{D}-3)^{2}}\right)^{2}=\left(\sqrt{10}\right)^{2}\\\\&\Leftrightarrow&1+(y_{D}-3)^{2}=10\\\\&\Leftrightarrow&(y_{D}-3)^{2}=10-1\\\\&\Leftrightarrow&(y_{D}-3)^{2}=9\\\\&\Leftrightarrow&\sqrt{(y_{D}-3)^{2}}=\sqrt{9}\\\\&\Leftrightarrow&\left|y_{D}-3\right|=3\\\\&\Leftrightarrow&\left|y_{D}-3\right|=3\\\\&\Leftrightarrow&y_{D}-3=3\quad\text{ou}\quad y_{D}-3=-3\\\\&\Leftrightarrow&y_{D}=3+3\quad\text{ou}\quad y_{D}=-3+3\\\\&\Leftrightarrow&y_{D}=6\quad\text{ou}\quad y_{D}=0\end{array}$
Comme l'ordonnée de $D$ est différent de $0$ alors, on trouve : $\boxed{y_{D}=6}$
D'où,
$$\boxed{D\begin{pmatrix} 0\\6\end{pmatrix}}$$

Exercice de Synthèse
Dans le plan muni d'un repéré orthonormal, on donne les points
$$A(2\;;\ 1)\;,\ B(-3\;;\ 2)\ \text{ et }\ C(-2\;;\ 7)$$
1) Plaçons les points dans le repère

2) Calculons les coordonnées de $\overrightarrow{AB}\;,\ \overrightarrow{BC}\ $ et $\ \overrightarrow{AC}$
On a :
$\overrightarrow{AB}\begin{pmatrix} -3-2\\2-1\end{pmatrix}=\begin{pmatrix} -5\\1\end{pmatrix}$
$\overrightarrow{BC}\begin{pmatrix} -2-(-3)\\7-2\end{pmatrix}=\begin{pmatrix} 1\\5\end{pmatrix}$
$\overrightarrow{AC}\begin{pmatrix} -2-2\\7-1\end{pmatrix}=\begin{pmatrix} -4\\6\end{pmatrix}$
Donc,
$$\boxed{\overrightarrow{AB}\begin{pmatrix} -5\\1\end{pmatrix}\;,\quad\overrightarrow{BC}\begin{pmatrix} 1\\5\end{pmatrix}\;,\quad\overrightarrow{AC}\begin{pmatrix} -4\\6\end{pmatrix}}$$
3) Montrons $ABC$ est un triangle rectangle en $B$
Pour cela, il suffit de montrer que les vecteurs $\overrightarrow{AB}\ $ et $\ \overrightarrow{BC}$ sont orthogonaux.
On a :
$\begin{array}{rcl} (x_{_{\overrightarrow{AB}}}\times x_{_{\overrightarrow{BC}}})+(y_{_{\overrightarrow{AB}}}\times y_{_{\overrightarrow{BC}}})&=&[(-5)\times 1]+[1\times 5]\\\\&=&-5+5\\\\&=&0\end{array}$
Donc, $\boxed{(x_{_{\overrightarrow{AB}}}\times x_{_{\overrightarrow{BC}}})+(y_{_{\overrightarrow{AB}}}\times y_{_{\overrightarrow{BC}}})=0}$
Ce qui signifie que les coordonnées des vecteurs $\overrightarrow{AB}\ $ et $\ \overrightarrow{BC}$ vérifient la condition d'orthogonalité.
Par conséquent, les vecteurs $\overrightarrow{AB}\ $ et $\ \overrightarrow{BC}$ sont orthogonaux en $B.$
D'où, $ABC$ est un triangle rectangle en $B.$
4) Calculons les coordonnées du point $E$ tel que $ABEC$ soit un parallélogramme
On a : $ABEC$ un parallélogramme alors, $\overrightarrow{CE}=\overrightarrow{AB}$
Soit :
$\overrightarrow{CE}\begin{pmatrix} x_{E}-(-2)\\y_{E}-7\end{pmatrix}=\begin{pmatrix} x_{E}+2\\y_{E}-7\end{pmatrix}$
$\overrightarrow{AB}=\begin{pmatrix} -5\\1\end{pmatrix}$
Donc, on a :
$\begin{array}{rcl}\overrightarrow{CE}=\overrightarrow{AB}&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{E}+2&=&-5\\\\y_{E}-7&=&1\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{E}&=&-5-2\\\\y_{E}&=&1+7\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{E}&=&-7\\\\y_{E}&=&8\end{array}\right.\end{array}$
D'où,
$$\boxed{E\begin{pmatrix} -7\\8\end{pmatrix}}$$
5) Soit $F$ l'image de $B$ par la translation de vecteur $\overrightarrow{CE}.$
Calculons les coordonnées de $F$
On a : $F=t_{\overrightarrow{CE}}(B).$
Cela signifie que : $\overrightarrow{BF}=\overrightarrow{CE}$
Soit :
$\overrightarrow{CE}=\begin{pmatrix} -5\\1\end{pmatrix}$
$\overrightarrow{BF}\begin{pmatrix} x_{F}-(-3)\\y_{F}-2\end{pmatrix}=\begin{pmatrix} x_{F}+3\\y_{E}-2\end{pmatrix}$
Alors, on a :
$\begin{array}{rcl}\overrightarrow{BF}=\overrightarrow{CE}&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{F}+3&=&-5\\ \\y_{F}-2&=&1\end{array}\right.\\ \\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{F}&=&-5-3\\ \\y_{F}&=&1+2\end{array}\right.\\ \\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{F}&=&-8\\ \\y_{F}&=&3\end{array}\right.\end{array}$
Ainsi,
$$\boxed{F\begin{pmatrix} -8\\3\end{pmatrix}}$$
6) Justifions que $B$ est le milieu de $[AF]$
$ABEC$ étant un parallélogramme alors, $\overrightarrow{AB}=\overrightarrow{CE}$
Or, d'après le résultat de la question $5)$, on a : $\overrightarrow{BF}=\overrightarrow{CE}$
Donc, $\overrightarrow{AB}=\overrightarrow{CE}=\overrightarrow{BF}$
Par suite, $\overrightarrow{AB}=\overrightarrow{BF}$
D'où, $B$ est milieu de $[AF]$
7) Soit $\overrightarrow{MN}$ un vecteur de coordonnées $\overrightarrow{MN}\left(\dfrac{5}{3}\;;\ -\dfrac{1}{3}\right)$
a) Démontrons que $\overrightarrow{AB}=-3\overrightarrow{MN}$
Soit : $\overrightarrow{MN}\begin{pmatrix} \dfrac{5}{3}\\ \\-\dfrac{1}{3}\end{pmatrix}$ alors, les coordonnées du vecteur $-3\overrightarrow{MN}$ sont obtenues en multipliant celles du vecteur $\overrightarrow{MN}$ par $-3.$
On obtient :
$$-3\begin{pmatrix}\dfrac{5}{3}\\ \\-\dfrac{1}{3}\end{pmatrix}=\begin{pmatrix} -3\times\dfrac{5}{3}\\ \\(-3)\times\left(\dfrac{-1}{3}\right)\end{pmatrix}=\begin{pmatrix} -5\\ \\1\end{pmatrix}$$
Ainsi, $-3\overrightarrow{MN}$ un vecteur de coordonnées $-3\overrightarrow{MN}\begin{pmatrix} -5\\ \\1\end{pmatrix}.$
Or, d'après le résultat de la question $2)$, on a : $\overrightarrow{AB}\begin{pmatrix} -5\\ \\1\end{pmatrix}.$
Ainsi, on remarque que les vecteur $-3\overrightarrow{MN}\ $ et $\ \overrightarrow{AB}$ ont les mêmes coordonnées.
Par conséquent, ces deux vecteurs sont égaux.
D'où, $\boxed{\overrightarrow{AB}=-3\overrightarrow{MN}}$
b) Vérifions que $\overrightarrow{AB}\ $ et $\ \overrightarrow{MN}$ sont colinéaires
D'après le résultat de la question $7)\;a)$, on a : $\overrightarrow{AB}=k\overrightarrow{MN}$ avec, $k=-3\in\mathbb{R}$
Ce qui justifie que $\overrightarrow{AB}\ $ et $\ \overrightarrow{MN}$ sont colinéaires.
Autrement, soit :
$\begin{array}{rcl} (x_{_{\overrightarrow{AB}}}\times y_{_{\overrightarrow{MN}}})-(x_{_{\overrightarrow{MN}}}\times y_{_{\overrightarrow{AB}}})&=&\left[(-5)\times\left(-\dfrac{1}{3}\right)\right]-\left[\left(\dfrac{5}{3}\right)\times 1\right]\\\\&=&\dfrac{5}{3}-\dfrac{5}{3}\\\\&=&0\end{array}$
Donc, $\boxed{(x_{_{\overrightarrow{AB}}}\times y_{_{\overrightarrow{MN}}})-(x_{_{\overrightarrow{MN}}}\times y_{_{\overrightarrow{AB}}})=0}$
Ce qui signifie que les coordonnées des vecteurs $\overrightarrow{AB}\ $ et $\ \overrightarrow{MN}$ vérifient la condition de colinéarité.
Par conséquent, les vecteurs $\overrightarrow{AB}\ $ et $\ \overrightarrow{MN}$ sont colinéaires.
Auteur:
Diny Faye

Commentaires
Anonyme (non vérifié)
lun, 06/29/2020 - 21:42
Permalien
Bonsoir je suis une élève de
Khady Fall (non vérifié)
lun, 05/09/2022 - 08:49
Permalien
Je veux faire un exercice sur
Anonyme (non vérifié)
mer, 05/11/2022 - 17:52
Permalien
Exercice 16
Anonyme (non vérifié)
mer, 07/22/2020 - 20:45
Permalien
Bonjour l'exo 35 la
Alhassane (non vérifié)
ven, 08/28/2020 - 02:51
Permalien
Salue j'ai fini l'exo n4 mais
fatbinetou tall (non vérifié)
mer, 09/02/2020 - 22:26
Permalien
l'exo 39 svp
Anonyme (non vérifié)
lun, 04/19/2021 - 20:47
Permalien
De même que moi j ai op vu l
Anonyme (non vérifié)
jeu, 07/08/2021 - 08:42
Permalien
Salut je suis une élève de
Aminata Diagne (non vérifié)
jeu, 07/29/2021 - 23:01
Permalien
Bonsoir aidez-moi svp je de
Khady Fall (non vérifié)
lun, 05/09/2022 - 09:02
Permalien
Bonjour aider_moi math je de
sokhna mai diouf (non vérifié)
sam, 07/16/2022 - 19:06
Permalien
bonjour pourais-je avoir la
ANANNYME (non vérifié)
mer, 08/31/2022 - 20:32
Permalien
svp pourais je avoir la
Ajouter un commentaire