Solution des exercices : repérage - 2nd

Classe:

Seconde

Mesures algébriques

Exercice 1

Les points

$A\;,\ B\;,\ C\$ et

$\ D$ sont situés sur un axe de telle sorte que :

$\overline{AB}=-8\;;\quad \overline{BC}=12\ \text{ et }\ \overline{CD}=-6$

Calculons

$\overline{AC}\;,\ \overline{AD}\;,\ \overline{BA}\;,\ \overline{BD}\;,\ \overline{DA}\$ et

$\ \overline{DB}.$

$-\$ Calcul de

$\overline{AC}$

D'après la relation de Chasles, on a :

$\overline{AC}=\overline{AB}+\overline{BC}$

Or,

$\overline{AB}=-8\$ et

$\ \overline{BC}=12$

Donc,

$\overline{AC}=-8+12=4$

D'où,

$\boxed{\overline{AC}=4}$

$-\$ Calcul de

$\overline{AD}$

De la même manière, en utilisant la relation de Chasles, on obtient :

$\begin{array}{rcl}\overline{AD}&=&\overline{AC}+\overline{CD}\\ \\&=&4-6\\ \\&=&-2\end{array}$

Ainsi,

$\boxed{\overline{AD}=-2}$

$-\$ Calcul de

$\overline{BA}$

On a :

$\overline{BA}=-\overline{AB}$

Or,

$\overline{AB}=-8$ donc,

$\overline{BA}=-(-8)=8$

D'où,

$\boxed{\overline{BA}=8}$

$-\$ Calcul de

$\overline{BD}$

On a :

$\begin{array}{rcl}\overline{BD}&=&\overline{BA}+\overline{AD}\\ \\&=&8-2\\ \\&=&6\end{array}$

Par suite,

$\boxed{\overline{BD}=6}$

$-\$ Calcul de

$\overline{DA}$

On a :

$\overline{DA}+\overline{AD}=0$

Donc,

$\overline{DA}=-\overline{AD}=-(-2)=2$

Ainsi,

$\boxed{\overline{DA}=2}$

$-\$ Calcul de

$\overline{DB}$

On a :

$\overline{DB}=-\overline{BD}=-6$

Donc,

$\boxed{\overline{DB}=-6}$

Exercice 2

Sur un axe

$(D)$ , on donne trois points

$A\;,\ B\$ et

$\ C$ tels que

$\overline{AB}=-9\$ et

$\ \overline{BC}=16.$

Déterminons la position de l'origine

$O$ pour que

$\overline{OA}+3\overline{OB}+5\overline{OC}=0$

En utilisant la relation de Chasles, on obtient :

$\overline{OB}=\overline{OA}+\overline{AB}$

Donc,

$3\overline{OB}=3\overline{OA}+3\overline{OB}$

De la même manière, on obtient :

$\overline{OC}=\overline{OA}+\overline{AC}$

Donc,

$5\overline{OC}=5\overline{OA}+5\overline{AC}$

Par suite,

$\begin{array}{rcl}\overline{OA}+3\overline{OB}+5\overline{OC}=0&\Leftrightarrow&\overline{OA}+3\overline{OA}+3\overline{AB}+5\overline{OA}+5\overline{AC}=0\\\\&\Leftrightarrow&9\overline{OA}+3\overline{AB}+5\overline{AC}=0\\\\&\Leftrightarrow&9\overline{OA}=-3\overline{AB}-5\overline{AC}\\\\&\Leftrightarrow&\overline{OA}=-\dfrac{3\overline{AB}}{9}-\dfrac{5\overline{AC}}{9}\end{array}$

Donc, le point

$O$ est tel que :

$\overline{OA}=-\dfrac{3\overline{AB}}{9}-\dfrac{5\overline{AC}}{9}$

Or, D'après la relation de Chasles, on a :

$\begin{array}{rcl}\overline{AC}&=&\overline{AB}+\overline{BC}\\ \\&=&-9+16\\ \\&=&7\end{array}$

Par suite, en remplaçant

$\overline{AB}\$ et

$\ \overline{AC}$ dans l'expression de

$\overline{OA}$ , on obtient :

$\begin{array}{rcl}\overline{OA}&=&-\dfrac{3\times(-9)}{9}-\dfrac{5\times 7}{9}\\ \\&=&\dfrac{27}{9}-\dfrac{35}{9}\\ \\&=&-\dfrac{8}{9}\end{array}$

Ainsi, la position de l'origine

$O$ du repère est tel que :

$\boxed{\overline{OA}=-\dfrac{8}{9}}$

Exercice 5

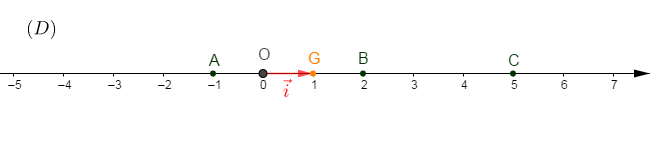
Sur un axe

$(D)$ , on considère deux points

$A\$ et

$\ B$ d'abscisses respectives

$-1\$ et

$\ 2.$

1) Plaçons le point

$C$ tel que

$\overline{CA}=2\overline{CB}.$

Considérons un repère

$(O\;,\ \vec{i})$ associé à l'axe

$(D)$ avec

$\vec{i}$ vecteur unitaire.

En effet, on a :

$\begin{array}{rcl}\overline{CA}=2\overline{CB}&\Leftrightarrow&\overline{CA}-2\overline{CB}=0\\\\&\Leftrightarrow&\overline{CO}+\overline{OA}-2\overline{CO}-2\overline{OB}=0\\\\&\Leftrightarrow&-\overline{CO}+\overline{OA}-2\overline{OB}=0\\\\&\Leftrightarrow&-\overline{CO}=-\overline{OA}+2\overline{OB}\\\\&\Leftrightarrow&\overline{OC}=-\overline{OA}+2\overline{OB}\\\\&\Leftrightarrow&\overline{OC}=1+4\\\\&\Leftrightarrow&\overline{OC}=5\end{array}$

Donc,

$C$ est tel que :

$\boxed{\overline{OC}=5}$

D'où,

$C$ est d'abscisse

$5$

2) Montrons qu'il existe un point

$M$ tel que :

$\overline{MA}+2\overline{MB}=0.$

Soit le système de points pondérés :

$\{(A\;;\ 1)\;,\ (B\;;\ 2)\}$

On a :

$1+2=3\neq 0$ donc, ce système admet un barycentre

$G$ vérifiant :

$\overrightarrow{GA}+2\overrightarrow{GB}=\vec{0}$

Cette relation peut encore s'écrire, en tenant compte des mesures algébriques :

$\overline{GA}\cdot\vec{i}+2\overline{GB}\cdot\vec{i}=\vec{0}\ \Leftrightarrow\ (\overline{GA}+2\overline{GB})\cdot\vec{i}=\vec{0}$

Or,

$\vec{i}$ étant un vecteur non nul donc,

$(\overline{GA}+2\overline{GB})\cdot\vec{i}=\vec{0}\ \Leftrightarrow\ \overline{GA}+2\overline{GB}=0$

Donc, il existe bien un point

$M=G$ vérifiant :

$\overline{MA}+2\overline{MB}=0.$

Soit :

$\begin{array}{rcl}\overline{OG}&=&\dfrac{\overline{OA}}{3}+2\dfrac{\overline{OB}}{3}\\\\&=&-\dfrac{1}{3}+\dfrac{4}{3}\\\\&=&\dfrac{3}{3}\\\\&=&1\end{array}$

Donc,

$G$ est tel que :

$\boxed{\overline{OG}=1}$ c'est-à-dire ;

$G$ est d'abscisse

$1$

3) Déterminons les points

$M$ de

$(D)$ tels que

$MA^{2}-4MB^{2}=0$

On a :

$\begin{array}{rcl}MA^{2}-4MB^{2}=0&\Leftrightarrow&(\overline{MA}-2\overline{MB})\cdot(\overline{MA}+2\overline{MB})=0\\\\&\Leftrightarrow&\overline{MA}-2\overline{MB}=0\quad\text{ou}\quad\overline{MA}+2\overline{MB}=0 \end{array}$

Or, d'après les questions précédentes, les points

$M$ de

$(D)$ vérifiant respectivement :

$\overline{MA}-2\overline{MB}=0\$ et

$\ \overline{MA}+2\overline{MB}=0$ sont respectivement les point

$C\$ et

$\ G.$

D'où, l'ensemble

$\mathbf{E}$ des points

$M$ de

$(D)$ tels que

$MA^{2}-4MB^{2}=0$ est donné par :

$\mathbf{E}=\{C\;,\ G\}$

Auteur:

Diny Faye

Commentaires

Lidy (non vérifié)

lun, 03/22/2021 - 09:00

Permalien

Merci

Merci pour les exercices çà m'a bien aidé

répondre

fatbintou seconde SB (non vérifié)

lun, 04/19/2021 - 22:20

Permalien

avis

Votre site est mon préfèré pour travailler. La correction de exercices nous aide beaucoup. Par contre tous les exercices n'en ont pas, ce qui est déplorable. S'il vous plait aider nous. Ne nous laissez pas dans le doute d'avoir trouvé ou pas