Série d'exercices sur le Calcul vectoriel, Repères et Barycentres 1e S

Vecteurs

Exercice 1

1) Démontrer que le point $I$ est milieu du segment $[AB]$ si et seulement si :
$$\overrightarrow{IA}+\overrightarrow{IB}=\vec{O}$$

2) Avec les mêmes notations qu'au $1^{\circ}$, démontrer que :

$$\overrightarrow{AI}=\dfrac{1}{2}\overrightarrow{AB}\qquad\text{et que}\qquad\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}$$

3) Soit $ABC$ un triangle, $E$ le milieu de $[AB]$, $F$ le milieu de $[AC]$.

Démontrer que :
$$\overrightarrow{EF}=\dfrac{1}{2}\overrightarrow{BC}$$

En déduire que :

a) $(EF)\parallel (BC)$

b) $EF=\dfrac{1}{2}BC$

(Théorème de la droite des milieux)

4) Soient $A\;,\ B\;,\ C\text{ et }D$ 4 points, $I$ le milieu de $[AC]$, $J$ le milieu de $[BD]$
 
Démontrer que $2\overrightarrow{IJ}=\overrightarrow{AB}+\overrightarrow{CD}$

Comment choisir le quadrilatère $ABCD$ pour que $I$ et $J$ soient confondus ?

5) Déterminer l'ensemble des points $M$ du plan tels que :

$a)\ ||\overrightarrow{MA}+\overrightarrow{MB}||=||\overrightarrow{AC}||\quad b)\ ||\overrightarrow{MA}+\overrightarrow{MB}||=2MC$

c) $\overrightarrow{MA}+\overrightarrow{MB}$ a même direction que $\overrightarrow{BC}$

Exercice 2

Soient $ABCD\text{ et }AECF$ des parallélogrammes.

Que peut-on dire des vecteurs $\overrightarrow{BE}\text{ et }\overrightarrow{FD}$

Exercice 3

Soient $A\;,\ B\;,\ C\text{ et }D$ des points du plan et $I$ et $J$ les milieux respectifs de $[AC]\text{ et }[BD]$.

Démontrer que :

$\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{CB}=2\overrightarrow{IJ}$

Exercice 4

Soient $ABC$ un triangle dont $O$ est le centre de gravité.

Si $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\vec{O}$, que peut-on dire du triangle $ABC$ ?

Exercice 5

Soient $\vec{u}\;,\ \vec{v}\text{ et }\vec{w}$ 3 vecteurs tels que :

$(1)\ \vec{u}+\vec{v}+\vec{w}=\vec{O}\qquad (2)\ ||\vec{v}||=\lambda||\vec{u}||\qquad (3)\ ||\vec{w}||=(\lambda+1)||\vec{u}||$

Démontrer que $\vec{u}\;,\ \vec{v}\;,\ \vec{w}$ sont colinéaires.

Exprimer $\vec{v}\text{ et }\vec{w}$ en fonction de $\vec{u}$

Exercice 6

On donne un triangle $ABC$ et les milieux respectifs

$A'\;,\ B'\text{ et }C'\text{ de }[BC]\;,\ [CA]\text{ et }[AB]$

Un point $M$ quelconque étant donné, on considère les points $N\text{ et }P$ tels que :
$$\overrightarrow{MN}=\overrightarrow{CC'}\qquad\text{et}\qquad\overrightarrow{MP}=-\overrightarrow{BB'}$$

1) Démontrer que les droites $(NP)\text{ et }(AA')$ sont parallèles.

2) Soit $I$ le milieu de $[NP]$.

Comparer les vecteurs $\overrightarrow{MI}\text{ et }\overrightarrow{BC}$

En déduire que les droites $(MI)\text{ et }(BC)$ sont parallèles.

Exercice 7

On considère deux triangles $ABC\text{ et }A'B'C'$ et leurs centres de gravité respectifs $G\text{ et }G'$

1) Démontrer que :
$$\overrightarrow{AA'}+\overrightarrow{BB'}+\overrightarrow{CC'}=3\overrightarrow{GG'}$$

2) En déduire une condition nécessaire te suffisante pour que les triangles aient même centre de gravité.

3) Comparer $G\text{ et }G'$ dans les cas suivants :

$a)\ A'\;,\ B'\text{ et }C'$ sont les milieux respectifs de $[BC]\;,\ [CA]\text{et}[AB]$

$b)\ A'\;,\ B'\text{ et }C'$ sont respectivement les points définis par :

$\overrightarrow{BA'}=t\overrightarrow{BC}\;;\ \overrightarrow{CB'}=t\overrightarrow{CA}\;;\ \overrightarrow{AC'}=t\overrightarrow{AB}$, où $t$ est un réel non nul.

$\left(\text{Faire une figure avec }t=\dfrac{3}{2}\right)$

Exercice 8

Soient $A\;,\ B\;,\ C\text{ et }D$ 4 points du plan.

A tout réel $t$, on associe les points $M\text{ et }N$ tels que :
$$\overrightarrow{AM}=t\overrightarrow{AB}\text{ et }\overrightarrow{DN}=t\overrightarrow{DC}$$

1) Démontrer que $\overrightarrow{MN}=t\overrightarrow{BC}+(1-t)\overrightarrow{AD}$

2) On suppose désormais que :

$\overrightarrow{BC}=3\overrightarrow{AD}$ et note $AD=||\overrightarrow{AD}||=a$

Exprimer le vecteur $\overrightarrow{MN}$ en fonction de $t\text{ et }\overrightarrow{AD}$

puis la distance $MN$ en fonction de $t\text{ et }a$

3) Pour quelles valeurs de $t$ a-t-on :

a) $M=N$ ?

b) $MN=\dfrac{7}{2}a ?$

Exercice 9

$ABCD$ est un quadrilatère.

1) $I\text{ et }J$ sont les milieux de $[AB]\text{ et }[CD]$.

Démontrer que : $2\overrightarrow{IJ}=\overrightarrow{AD}+\overrightarrow{BC}$

2) $P\text{ et }U$ sont tels que : $\overrightarrow{AP}=\overrightarrow{UP}=\overrightarrow{UD}$

$R\text{ et }V$ sont tels que : $\overrightarrow{BR}=\overrightarrow{RV}=\overrightarrow{VC}$

$S\text{ et }K$ sont tels que : $\overrightarrow{IS}=\overrightarrow{SK}=\overrightarrow{KJ}$

Démontrer que $S$ est le milieu de $[PR]\text{ et }K$ celui de $[UV]$.

Exercice 10

Droite et cercle d'Euler d'un triangle

Soit $ABC$ un triangle, $A'\;,\ B'\text{ et }C'$ les milieux respectifs de

$[BC]\;,\ [CA]\text{ et }[AB]\;,\ O$ le centre du cercle circonscrit et $G$ le centre de gravité.

1) Montrer qu'il existe un point $H$ unique tel que :
$$\overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\quad(1)$$

2) Montrer que

$\overrightarrow{AH}=2\overrightarrow{OA'}\;;\ \overrightarrow{BH}=2\overrightarrow{OB'}\;;\ \overrightarrow{CH}=2\overrightarrow{OC'}$

3) Démontrer que $H$ est l'orthocentre du triangle $ABC.$

4) En utilisant la relation $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\vec{0}$

démontrer que $\overrightarrow{OH}=3\overrightarrow{OG}$

En déduire que les trois points $O\:,\ G\text{ et }H$ sont alignés.

(La droite portant ces trois points est appelée droite d'Euler du triangle).

5) Soit $A_{1}$ le symétrique de $A$ par rapport à $O$ et $I$ le milieu de $[HA_{1}]$

Démontrer que $2\overrightarrow{OI}=\overrightarrow{AH}$, puis que $I=A'$.

En conclure que $A_{1}$ est aussi le symétrique de $H$ par rapport à $A'$.

6) Déduire de la question précédente le théorème suivant :

Les symétriques de l'orthocentre par rapport aux milieux des cotés du triangle appartiennent au cercle circonscrit.

7) Soit $\Omega$ l'isobarycentre de $A\:,\ B\;,\ C\text{ et }H$ et $U$ le milieu de $[HA]$, $\ V$ le milieu de $[HB]$, $\ W$ le milieu de $[HC]$ $\ (U\;,\ V\text{ et }W$ sont les points d'Euler)

a) Montrer en utilisant la relation (1) que $\Omega$ est le milieu de $[OH]$.

b) Établir les égalités :
$$\overrightarrow{\Omega U}=-\overrightarrow{\Omega A'}=\dfrac{1}{2}\overrightarrow{OA}\;;\qquad \overrightarrow{\Omega V}=-\overrightarrow{\Omega B'}=\dfrac{1}{2}\overrightarrow{OB}$$

$$\overrightarrow{\Omega W}=-\overrightarrow{\Omega C'}=\dfrac{1}{2}\overrightarrow{OC}$$

En déduire que les milieux $A'\;,\ B'\text{ et }C$ et les points d'Euler $U\;,\ V\text{ et }W$ appartiennent au cercle de centre $\omega$ admettant pour rayon la moitié du rayon du cercle circonscrit au triangle.

8) Montrer que ce cercle passe par les points $\alpha\;,\ \beta\text{ et }\gamma$, intersections respectives des hauteurs $(AH)\;,\ (BH)\text{ et }(CH)$ avec les cotés $[BC]\;,\ [CA]\text{ et }[AB]$ ( cercle des neuf points)

Mesures algébriques

Exercice 11

$\Delta$ est un axe muni d'un repère $(O\;,\ I)$.

Soient $A\text{ et }B$ deux points de $\Delta$ d'abscisses respectives 6 et -2.

1) Calculer l'abscisse du point $M$ de $\Delta$ tel que $\dfrac{\overline{MA}}{\overline{MB}}=\dfrac{5}{3}$

Calculer $\overline{MA}\text{ et }\overline{MB}$

2) Calculer l'abscisse du point $N$ de $\Delta$ tel que $\dfrac{\overline{NA}}{\overline{NB}}=-\dfrac{5}{3}$.

Calculer $\overline{NA}\text{ et }\overline{NB}$.

3) Calculer l'abscisse de $I$ milieu de $[MN]$

Calculer $\dfrac{\overline{IA}}{\overline{IB}}$

Exercice 12

Soient $A\;,\ B\;,\ C\text{ et }M$ 4 points d'une même droite $(D)$ munie d'un repère $(O\;,\ I)$

En observant que l'on a : $\overline{MA}=\overline{MC}+\overline{CA}\text{ et }\overline{MB}=\overline{MC}+\overline{CB}$,

1) Former l'expression $\overline{MA}\cdot\overline{BC}+\overline{MB}\cdot\overline{CA}$

et en déduire la relation d'Euler :
$$\overline{MA}\cdot\overline{BC}+\overline{MB}\cdot\overline{CA}+\overline{MC}\cdot\overline{AB}=0$$

2) Former l'expression $MA^{2}\cdot\overline{BC}+MB^{2}\cdot\overline{CA}$

et en déduire la relation de Stewart :
$$MA^{2}\cdot\overline{BC}+MB^{2}\cdot\overline{CA}+MC^{2}\cdot\overline{AB}+\overline{BC}\cdot\overline{CA}\cdot\overline{AB}=0$$

Exercice 13

Soient $A\;,\ B\;,\ C\text{ et }D$ 4 points d'un axe $\Delta$ de repère $(O\;,\ I)$.On désigne par $a\;,\ b\;,\ c\text{ et }d$ leurs abscisses respectives

c'est-à-dire que : $\overline{OA}=a\;,\ \overline{OB}=b\;,\ \overline{OC}=c\;,\ \overline{OD}=d$

On appelle birapport des 4 points $A\;,\ B\;,\ C\;,\text{ et }D$ dans cet ordre et on note $(ABCD)$ l'expression : $$(ABCD)=\dfrac{\overline{CA}}{\overline{CB}}:\dfrac{\overline{DA}}{\overline{DB}}$$

1) Exprimer le birapport $(ABCD)$ en fonction de $a\;,\ b\;,\ c\text{ et }d$.

2) Montrer que le birapport $(ABCD)$ reste invariant si on inverse simultanément chacun des couples $(AB)\text{ et }(CD)$ ou lorsqu'on échange ces deux couples.

3) L'ensemble ordonné des 4 points $A\;,\ B\;,\ C\text{ et }D$ est dit constituer une division harmonique lorsque le birapport $(ABCD)$ est égal à $-1$.

On dit alors que les points $C\text{ et }D$ sont conjugués harmoniques par rapport à $A\text{ et }B$

a) Utiliser $2^{\circ}$ pour montrer qu'alors les points $A\text{ et }B$ sont aussi conjugués harmoniques par rapport à $C\text{ et }D.$

b) Établir la relation $2(ab+cd)=(a+b)(c+d)$.

c) En prenant l'origine $O$ en $A$, démontrer la relation suivante, dite de NEWTON :
$$\dfrac{2}{\overline{AB}}=\dfrac{1}{\overline{AC}}+\dfrac{1}{\overline{AD}}$$

d) En prenant l'origine $O$ en $I$ milieu de $[AB]$, démontrer la relation suivante, dite de DESCARTES :

$\overline{IC}\cdot\overline{ID}=IA^{2}$.

Énoncés de Thalès

Exercice 14

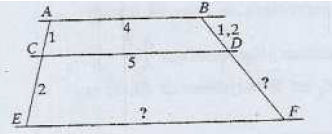
Les droites $(AB)\;,\ (CD)\text{ et }(EF)$ sont parallèles.

$AC=1\;,\ CE=2\;,\ AB=4\;,\ BD=1.2\text{ et }CD=5$.

Préciser les longueurs $DF\text{ et }EF$.

Exercice 15

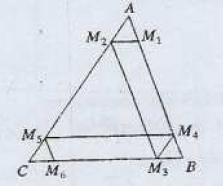
Dans un triangle $ABC$, $M_{1}$ est un point du segment $[AB]$ distinct des sommets $A\text{ et }B$.

On construit les points $M_{2}\;,\ M_{3}\;,\ M_{4}\;,\ M_{5}\text{ et }M_{6}$ tels que les droites $(M_{3}M_{4})\;,\ (M_{4}M_{5})\text{ et }(M_{5}M_{6})$ soient respectivement parallèles aux droites

$(BC)\;,\ (AB)\;,\ (AC)\;,\ (BC)\text{ et }(AB)$

Démontrer que la droite $(M_{1}M_{6})$ est parallèle à $(AC)$.

Exercice 16

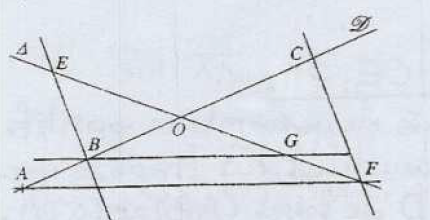
Théorème de Pappus

$(EB)$ est parallèle à $(CF)\text{ et }(BG)$ est parallèle à $(AF)$.

Montrer que $(AE)$ est parallèle à $(CG)$

Exercice 17

Étant donnés deux nombres positifs $a\text{ et }b$, on construit un trapèze convexe $ABCD$ de bases $(AB)\text{ et }(CD)\text{ et }J$ le projeté de $I$ sur $[BC]$ dans la direction des droites $(AB)\text{ et }(CD)$.

Montrer que : $\dfrac{1}{IJ}=\dfrac{1}{a}+\dfrac{1}{b}$

Exercice 18

$ABC$ est un triangle et $G$ son centre de gravité.

Une droite $\mathcal{D}$, ne contenant pas $G$, coupe respectivement les droites $(GA)\;,\ (GB)$

et $(GC)$ en $M\;,\ N\;,\ P$

Démontrer que :
$$\dfrac{\overline{GA}}{\overline{GM}}+\dfrac{\overline{GB}}{\overline{GN}}+\dfrac{\overline{GC}}{\overline{GP}}=0$$

On pourra utiliser la projection sur $(GA)$ parallèlement à $\mathcal{D}$

Exercice 19

Soient $D\text{ et }D'$ deux droites sécantes en $O$.

Soit $\Delta$ une droite ne passant pas par $O$ et qui coupe $D$ en $A\text{ et }D'$ en $B$.

Un point $M$ de $\Delta$ se projette en $E$ sur $D$ parallèlement à $D'$ et en $F$ sur $D'$ parallèlement à $D$.

1) Démontrer que :
$$\dfrac{\overline{OE}}{\overline{OA}}+\dfrac{\overline{OF}}{\overline{OB}}=1$$

2) Soient $E\text{ et }F$ deux points respectivement de $D\text{ et }D'$ et vérifiant la relation :

$$\dfrac{\overline{OE}}{\overline{OA}}+\dfrac{\overline{OF}}{\overline{OB}}=1$$

Soit $M$ le point tel que $OEFM$ soit un parallélogramme.

Démontrer que $M$ est sur la droite $\Delta$.

Exercice 20

Droites concourantes

$\mathcal{C}$ est un cercle de centre $O\text{ et }A\;,\ B\;,\ C\text{ et }D$ sont quatre points de ce cercle, tels que $ABCD$ ne soit pas un trapèze.

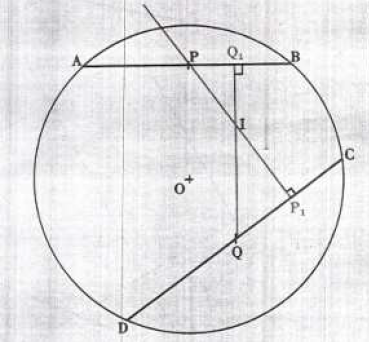
1) $P\text{ et }Q$ sont les milieux respectifs de $[AB]\text{ et }[CD]$.

La perpendiculaire à ($CD)$ passant par $P$ coupe $(CD)$ en $P_{1}$, la perpendiculaire à $(AB)$ passant par $Q$ coupe $(AB)$ en $Q_{1}$.

Les droites $(PP_{1})\text{ et }(QQ_{1})$ se coupent en $I.$

a) Démontrer que $OPIQ$ est un parallélogramme et que

$\overrightarrow{OP}=\dfrac{1}{2}(\overrightarrow{OA}+\overrightarrow{OB})$

b) En déduire que :
$$\overrightarrow{OI}=\dfrac{1}{2}(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD})$$
 
2) $R\text{ et }S$ sont les milieux respectifs de $[BC]\text{ et }[AD]$.

La perpendiculaire à $(BC)$ passant par $S$ coupe $(BC)$ en $S_{1}$, la perpendiculaire à $(AD)$ passant par $R$ coupe $(AD)$ en $R_{1}$.

Les droites $(RR_{1})\text{ et }(SS_{1})$ se coupent en $J.$

Démontrer que les points $I\text{ et }J$ sont confondus.

Exercice 21

Le parallélogramme de Wittenbauer

$ABCD$ est un quadrilatère convexe ; on partage chacun des cotés $[AB]\;,\ [BC]\;,\ [CD]$

et $[DA]$ en trois segments de même longueur et on joint deux à deux les points obtenus, comme indiqué sur la figure.

On obtient un quadrilatère $PQRS.$

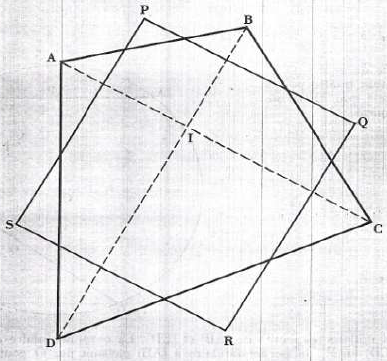
1) Démontrer que le quadrilatère $PQRS$ est un parallélogramme.

2) $I$ est le point d'intersection des diagonales $(AC)\text{ et }(BD)$ du quadrilatère $ABCD.$

Démontrer que : $\dfrac{2}{3}\overrightarrow{IA}+\dfrac{2}{3}\overrightarrow{IB}=\overrightarrow{IP}\qquad (1)$

3) $O$ est le centre du parallélogramme $PQRS$ et $G$ est l'isobarycentre du quadrilatère $ABCD.$

Démontrer que : $\overrightarrow{IO}=\dfrac{4}{3}\overrightarrow{IG}$

Indication :

on peut donner des relations comparables à la relation (1) pour les vecteurs $\overrightarrow{IQ}\;,\ \overrightarrow{IR}\;,\ \overrightarrow{IS}$ et utiliser ensuite la définition de l'isobarycentre.

4) A quelle condition le centre $O$ du parallélogramme $PQRS$ est-il confondu avec l'isobarycentre $G$ du quadrilatère $ABCD$ ?

Exercice 22

Théorèmes de MENELAUS et de CEVA

1) Théorème de Ménélaus

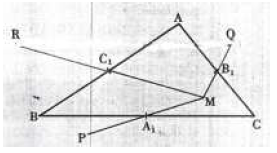
a) Soit $ABC$ un triangle.

Une droite $(D)$ coupe respectivement $(BC)\;,\ (CA)\text{ et }(AB)$ en $A'\;,\ B'\text{ et }C'$.

Soit $C_{1}$ le projeté de $C$ sur $(AB)$ parallèlement à $(D).$

Comparer les rapports

$\dfrac{\overline{A'B}}{\overline{A'C}}\text{ et }\dfrac{\overline{C'B}}{\overline{C'C_{1}}}\text{ puis }\dfrac{\overline{B'C}}{\overline{B'A}}\text{ et }\dfrac{\overline{C'C_{1}}}{\overline{C'A}}$

En déduire que :
$$\dfrac{\overline{A'B}}{\overline{A'C}}\times\dfrac{\overline{B'C}}{\overline{B'A}}\times\dfrac{\overline{C'A}}{\overline{C'B}}=1$$

b) Réciproquement, soient $A'\;,\ B'\;,\ C'$ trois points situés respectivement sur les cotés
$(BC)\;,\ (CA)\text{ et }(AB)$ du triangle $ABC.$

On désigne par $C''$ le point d'intersection de $(A'B')$ avec $(AB)$.

En utilisant a), comparer $\dfrac{\overline{C'A}}{\overline{C'B}}\text{ et }\dfrac{\overline{C''A}}{\overline{C''B}}$

En déduire que $C'=C''$, puis que $A'\;,\ B'\text{ et }C'$ sont alignés.

c) Conclusion : Pour trois points $A'\;,\ B'\text{ et }C'$ respectivement situés sur les cotés $(BC)\;,\ (CA)\text{ et }(AB)$ d'un triangle $ABC$, on a :

$A'\;,\ B'\;,\ C$ alignés $\Leftrightarrow\dfrac{\overline{A'B}}{\overline{A'C}}\times\dfrac{\overline{B'C}}{\overline{B'A}}\times\dfrac{\overline{C'A}}{\overline{C'B}}=1$

2) Théorème de Ceva

Soit $ABC$ un triangle, $A'\;,\ B'\;,\ C'$ trois points situés respectivement sur les cotés $(BC)\;,\ (CA)\text{ et }(AB)$ du triangle.

a) On suppose que les droites $(AA')\;,\ (BB')\text{ et }(CC')$ sont parallèles.

En utilisant le théorème de Thalès, montrer que :
$$\dfrac{\overline{A'B}}{\overline{A'C}}\times\dfrac{\overline{B'C}}{\overline{B'A}}\times\dfrac{\overline{C'A}}{\overline{C'B}}=-1$$

b) On suppose que les droites $(AA')\;,\ (BB')\text{ et }(CC')$ sont concourantes en un point $Q.$

Appliquer le théorème de Ménélaus au triangle $ACA'$ coupé par $(BQB')$ puis au triangle $ABA'$ coupé par $(CQC')$.

En déduire que :
$$\dfrac{\overline{A'B}}{\overline{A'C}}\times\dfrac{\overline{B'C}}{\overline{B'A}}\times\dfrac{\overline{C'A}}{\overline{C'B}}=-1$$

c) On suppose que les droites $(AA')\text{ et }(BB')$ sont parallèles et que :
$$\dfrac{\overline{A'B}}{\overline{A'C}}\times\dfrac{\overline{B'C}}{\overline{B'A}}\times\dfrac{\overline{C'A}}{\overline{C'B}}=-1$$

Soit $C''$ le point d'intersection de $(AB)$ avec la parallèle menée par $C$ à $(AA')$.

En utilisant a), conclure que $C''=C'.$

d) On suppose que les droites $(AA')\text{ et }(BB')$ se coupent en $Q$ et que :
$$\dfrac{\overline{A'B}}{\overline{A'C}}\times\dfrac{\overline{B'C}}{\overline{B'A}}\times\dfrac{\overline{C'A}}{\overline{C'B}}=-1$$

La droite $(QC)$ coupe $(AB)$ en $C''$.

En utilisant b), conclure que $C'=C''$.

e) Conclusion :

Pour trois points $A\;,\ B'\text{ et }C'$ respectivement situés sur les cotés $(BC)\;,\ (CA)$ et $(AB)$ d'un triangle $ABC$, on a : $\dfrac{\overline{A'B}}{\overline{A'C}}\times\dfrac{\overline{B'C}}{\overline{B'A}}\times\dfrac{\overline{C'A}}{\overline{C'B}}=-1$ si, et seulement si, ($(AA')\;,\ (BB)$ et $(CC')$ sont concourantes ou parallèles)

3) Application :

La droite de Newton

Les notations sont les mêmes qu'au $2^{\circ}$

Soient $(\Delta)$ une droite qui coupe les cotés

$(BC)\;,\ (CA)\text{ et }(AB)$ en $A'\;,\ B'\text{ et }C'$ respectivement,

et $A_{1}\;,\ B_{1}\text{ et }C_{1}$ les milieux respectifs de $[AA']\;,\ [BB']\text{ et }[CC']$.

Soient $I_{1}\;,\ I_{2}\text{ et }I_{3}$ les milieux respectifs de $[B'C']\;,\ [C'A]\text{ et }[AB']$.

a) Montrer que $$\overline{A_{1}I_{2}}=\dfrac{1}{2}\overline{A'C'}\text{ et }\overline{A_{1}I_{3}}=\dfrac{1}{2}\overline{A'B'}$$

En déduire que les points $A_{1}\;,\ I_{2}\text{ et }I_{3}$ sont alignés.

b) Montrer, de façon analogue, que $B_{1}\;,\ I_{3}\;,\ I_{1}$, d'une part, et $C_{1}\;,\ I_{1}\;,\ I_{2}$ sont alignés.

c) Appliquer le théorème de Ménélaus au triangle $AB'C'$ coupé par la droite portant les points $A'\;,\ B\text{ et }C$ et établir la relation :
$$\dfrac{\overline{A_{1}I_{3}}}{\overline{A_{1}I_{2}}}\times\dfrac{\overline{C_{1}I_{2}}}{\overline{C_{1}I_{1}}}\times\dfrac{\overline{B_{1}I_{1}}}{\overline{B_{1}I_{3}}}=1$$

d) Conclure que les trois points $A_{1}\;,\ B_{1}\text{ et }C_{1}$ sont alignés.

La droite qui porte ces trois points est appelée droite de Newton du quadrilatère complet formé par le triangle $ABC$ et la droite $AB'C'$.

N.B On appelle quadrilatère complet la figure formée par quatre droites deux à deux concourantes.

$(AA')\;,\ (BB')\text{ et }(CC')$ sont les diagonales du quadrilatère complet.

Le résultat que l'on vient de démontrer s'énonce aussi en disant que les milieux des diagonales d'un quadrilatère complet sont alignés.

Exercice 23

Soit $ABCD$ un parallélogramme non aplati.

1) Déterminer $b\text{ et }c$ réels tels que $D$ soit le barycentre de $\{(A\;,\ 1)(B\;,\ b)(C\;,\ c)\}$.

2) Les rées $b\text{ et }c$ ayant les valeurs obtenues et $H$ désignant le centre du parallélogramme, déterminer $h$, réel, pour que le barycentre de $\{(A\;,\ 1)(B\;,\ b)(C\;,\ c)(H\;,\ h)\}$ soit le milieu du segment $[HB]$.

Exercice 24

Soient $A\;,\ B\;,\ C$ 3 points non alignés du plan, $G$ le barycentre de

$\{(A\;,\ 1)(B\;,\ 2)(C\;,\ -1)\}\text{ et }M$ un point quelconque du plan. soient les vecteurs
$$\vec{u}=\overrightarrow{MA}+2\overrightarrow{MB}-\overrightarrow{MC}\text{ et }\vec{v}=2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}$$

1) Déterminer l'ensemble $\mathcal{E}$ des points $M$ du plan pour lesquels $\vec{u}\text{ et }\vec{v}$ sont colinéaires.

2) Déterminer l'ensemble $\mathcal{F}$ des points $M$ du plan pour lesquels
$$||\vec{u}||=||\vec{v}||$$

Exercice 25

$ABC$ est un triangle, $M$ est un point du plan.

$P\;,\ Q\;,\ R$ sont les symétriques de $M$ par rapport aux milieux $A_{1}\;,\ B_{1}\;,\ C_{1}$ des cotés $[BC]\;,\ [CA]\text{ et }[AB]$ du triangle.

$G\text{ et }K$ sont les centres de gravité des triangles $ABC\text{ et }PQR$.

1) Démontrer que $\overrightarrow{MP}=\overrightarrow{MB}+\overrightarrow{MC}$

En déduire que $\overrightarrow{MA}+\overrightarrow{MP}=3\overrightarrow{MG}$

2) Donner en fonction de $\overrightarrow{MG}$,

une expression de chacun des vecteurs suivants :
$$\overrightarrow{MB}+\overrightarrow{MQ}\;,\quad\overrightarrow{MC}+\overrightarrow{MR}\;,\quad\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\;,\quad\overrightarrow{MP}+\overrightarrow{MQ}+\overrightarrow{MR}$$

Démontrer que $G$ est le milieu de $[MK]$.

3) a) Démontrer que les triangles $ABC\text{ et }PQR$ ont leurs cotés parallèles deux à deux.

b) Démontrer que $\overrightarrow{PK}=\overrightarrow{GA}$

4) Les droites $(AP)\text{ et }(MG)$ se coupent en $L$.

a) Préciser la position de $L$ sur chacune des droites $(AP)\text{ et }(MG)$.

b) En déduire que les milieux des segments $[AP]\;,\ [BQ]\text{ et }[CR]$ sont confondus.

Quelle est la position relative des points $M\;,\ G\;,\ K\text{ et }L$ sur la droite $(MK)$ ?

Exercice 26

Soient $A\;,\ B\;,\ C$ 3 points du plan $\mathcal{P}$.

1) Déterminer l'ensemble des points $M$ de $\mathcal{P}$ tels que :
$$||3\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}||=||-\overrightarrow{MA}+3\overrightarrow{MB}-\overrightarrow{MC}||$$

2) Existe-t-il un point $M$ de $\mathcal{P}$ tel que :
$$||3\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}||=||-\overrightarrow{MA}+3\overrightarrow{MB}-\overrightarrow{MC}||=||-\overrightarrow{MA}-\overrightarrow{MB}+3\overrightarrow{MC}|| ?$$

3) Déterminer l'ensemble des points $M$ de $\mathcal{P}$ tels que :
$$||\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}||=||2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}||$$

Exercice 27

Soient $A\;,\ B\;,\ C$ 3 points non alignés et $\alpha\;,\ \beta\;,\ \gamma$ réels vérifiant les conditions d'existence des barycentres suivants :

$G$ barycentre de $\{(A\;,\ \alpha)(B\;,\ \beta)(C\;,\ \gamma)\}$ $G_{1}$ barycentre de $\{(A\;,\ -\alpha)(B\;,\ \beta)(C\;,\ \gamma)\}$

$G_{2}$ barycentre de $\{(A\;,\ \alpha)(B\;,\ \beta)(C\;,\ \gamma)\}$ $G_{3}$ barycentre de $\{(A\;,\ \alpha)(B\;,\ \beta)(C\;,\ \gamma)\}$.

1) Démontrer que les droites $(AG_{1})\;\ (BG_{2})\;,\ (CG_{3})$ concourent en $G$.

2) Démontrer que chacun des cotés du triangle $G_{1}G_{2}G_{3}$ passe par l'un des points $A\;,\ B\;,\ C.$

Exercice 28

Les points $A\;,\ B\;,\ C$ sont fixés et non alignés.

Soit $I$ le barycentre de $\{(A\;,\ 1)(B\;,\ -1)(C\;,\ 1)\}\text{ et }J$ le barycentre de $\{(A\;,\ -1)(C\;,\ 2)\}$.

1) Soit $M$ le barycentre de $\{(A\;,\ \alpha)(B\;,\ \beta)(C\;,\ \gamma)\}$.

Formuler une condition nécessaire et suffisante sur

$\alpha\;,\ \beta\;,\ \gamma$ pour que $I\;,\ J\;,\ M$ soient alignés.

2) La droite $(IJ)$ coupe $(BC)\text{ en }K\text{ et }(AB)\text{ en }L.$

Calculer $\dfrac{\overline{KB}}{\overline{KC}}\text{ et }\dfrac{\overline{LA}}{\overline{LB}}$

Déterminer $\lambda\text{ et }\mu$ pour que $L$ soit le barycentre de $\{(I\;,\ \lambda)(J\;,\ \mu)\}$.

Exercice 29

Soient $A\;,\ B\;,\ C$ 3 trois points non alignés du plan, $I$ le milieu de $[BC]\text{ et }M$ le barycentre du système $\{(A\;,\alpha)(B\;,\ \beta)(C\;,\gamma)\}$.

1) Formuler une condition nécessaire et suffisante sur $\alpha\;,\ \beta\;,\ \gamma$ pour que $M$ vérifie successivement :

a) $\overrightarrow{AM}$ est colinéaire à $\overrightarrow{BC}$

b) $\overrightarrow{IM}$ est colinéaire à $\overrightarrow{AB}$

2) $M$ satisfaisant à la fois aux conditions a) et b), la droite $(BM)$ coupe $(AC)$ en $J$ et la droite $(CM)$ coupe $(AB)$ en $K.$

Calculer les rapports
$$\dfrac{\overline{JA}}{\overline{JC}}\text{ et }\dfrac{\overline{KA}}{\overline{KB}}$$

Exercice 30

Soit $ABC$ un triangle et $M$ un point strictement intérieur à ce triangle.

Les droites $(AM)\;,\ (BM)\text{ et }(CM)$ coupent respectivement les cotés $[BC]\;,\ [CA]$ et $[AB]$ du triangle en $A'\;,\ B'\text{ et }C'$.

1) a) Démontrer que :
$$\dfrac{\text{aire}(MAB)}{\text{aire}(MAC)}=\dfrac{A'B}{A'C}$$

b) En déduire que $A'$ est le barycentre des points pondérés

$(B\;,\ \text{aire}(MAC))\text{et}(C\;,\ \text{aire}(MAB))$.

2) Soit $G$ le barycentre des points pondérés

$(A\;,\ \text{aire}(MBC)(B\;,\ \text{aire}(MAC))\text{et}(C\;,\ \text{aire}(MAB))$.

Démontrer que les points $G\text{ et }M$ sont confondus.

3) Soient $ABC$ un triangle, $\alpha\;,\ \beta\;,\ \gamma$ réels strictement positifs et $G$ le barycentre de $\{(A\;,\ \alpha)(B\;,\ \beta)(C\;,\ \gamma)\}$.

Démontrer, en utilisant les deux questions précédentes que :
$$\dfrac{\text{aire}(GBC)}{\alpha}=\dfrac{\text{aire}(GCA)}{\beta}=\dfrac{\text{aire}(GAB)}{\gamma}$$

4) Application :

Soit $I$ le centre du cercle inscrit dans le triangle $ABC.$

On pose : $BC=a\;,\ CA=b\text{ et }AB=c$.

En les résultats précédents, démontrer que $I$ est le barycentre des points $(A\;,\ a)\;,\ (B\;,\ b)\text{ et }(C\;,\ c)$.

5) On suppose désormais que les angles du triangle sont aigus.

Soit $H_{A}$ le pied de la hauteur issue de $A$ (donc $H_{A}$ est un point de $[BC]$).

a) Prouver que : $$\dfrac{\tan B}{\tan C}=\dfrac{H_{A}C}{H_{A}B}$$

en déduire que $H_{A}$ est le barycentre de $(B\;,\ \tan B)\text{ et }(C\;,\ \tan C)$

b) Établir que l'orthocentre $H$ du triangle $ABC$ est le barycentre de

$(A\;,\ \tan A)\;,\ (B\;,\ \tan B)\text{ et }(C\;,\ \tan C)$

Exercice 31

Déterminer graphiquement, ou analytiquement dans un repère convenablement choisi, le centre d'inertie de chacune des plaques homogènes, d'épaisseur constante et négligeable, suivantes :

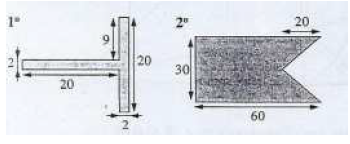
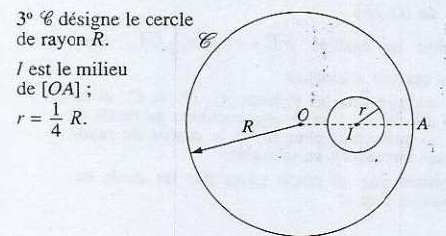
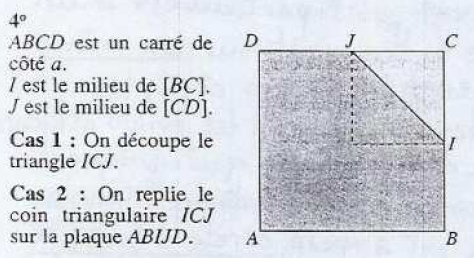
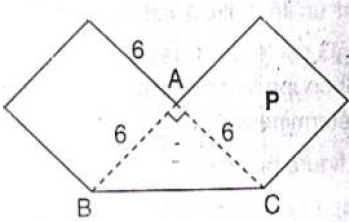
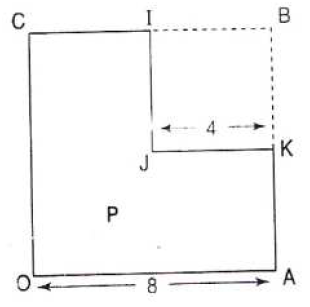
Exercice 32

Étant donné un triangle $ABC$, soient les points $M\text{ et }N$ définis par :
$$\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB}-\overrightarrow{AC}\text{ et }\overrightarrow{AN}=-\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}$$

1) Montrer que $(MN)$ est parallèle à $(BC)$

2) Donner les coordonnées de $M\text{ et }N$ dans les repères $(A\;,\ \overrightarrow{AB}\;,\ \overrightarrow{AC}\text{ puis }(B\;,\ \overrightarrow{BA}\;,\ \overrightarrow{BC})$

3) On définit maintenant les points $M\text{ et }N$ par :
$$\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB}+(1-k)\overrightarrow{AC}\text{ et }\overrightarrow{AN}=(1-k)\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\ (k\in\;\mathbb{R})$$

a) Exprimer

$\overrightarrow{MN}$ en fonction de $\overrightarrow{BC}$

b) Déterminer $k$ pour que $BCMN$ soit un parallélogramme.

Exercice 33

Soient $A\;,\ B\;,\ C$ non alignés.

$I$ le milieu de $[BC]$.

$\Delta$ une droite passant par $I$ et qui coupe $(AB)$ en $M\text{ et }(AC)\text{ en }N$.

$P$ est le point commun à $(BN)\text{ et }(CM)$.

Déterminer l'ensemble des points $P$ quand $\Delta$ pivote autour de $I$ en restant sécante à $(AB)\text{ et }(AC)$.

On pourra utiliser le repère $(A\;,\ \overrightarrow{AB}\;,\ \overrightarrow{AC})$

Exercice 34

Soient un triangle $OAB$ et deux points $C\text{ et }D$ alignés avec $O$.

Un point $M$ de la droite $(AB)$ est variable.

$(MC)$ coupe $(OA)\text{ en }N\text{ et }(MD)\text{ coupe }(OB)\text{ en }P$.

Démontrer que la droite $(NP)$ passe par un point fixe.

N.B On pourra rapporter le plan à un repère bien choisi.

Exercice 35

$ABCD$ est un parallélogramme.

Une parallèle à $(AB)\text{ coupe }(AD)\text{ en }I\text{ et }(BC)\text{ en }J$ ;

une parallèle à $(AD)\text{ coupe }(AB)\text{ en }E\text{ et }(CD)\text{ en }F$.

On se propose de montrer que les droites $(AC)\;,\ (EJ)\text{ et }(IF)$ sont soit parallèles, soit concourantes.

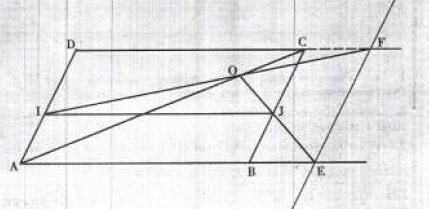
1) Faire une figure sur laquelle les droites $(AC)\;,\ (EJ)\text{ et }(IF)$ sont parallèles.

2) On choisit $(A\;,\ \overrightarrow{AB}\;,\ \overrightarrow{AD})$ pour repère.

a) Quelles sont les coordonnées de $A\;,\ B\;,\ C\;,\ D$ ?

Quelles sont les abscisses de $I\text{ et }J$ ?

Quelles sont les ordonnées de $E\text{ et }F$ ?

b) On désigne par $a$ l'abscisse de $E$ et par $b$ l'ordonnée de $I$.

Déterminer une équation cartésienne de chacune des droites $(AC)\;,\ (IF)\text{ et }(EJ)$.

c) Démontrer que si les droites $(AC)\text{ et }(IF)$ sont parallèles alors les droites $(AC)\;,\ (IF)\text{ et }(EJ)$ sont parallèles

d) Démontrer que si les droites $(AC)\text{ et }(IF)$ sont sécantes en $O$, alors les droites $(AC)\;,\ (IF)\text{ et }(EJ)$ sont concourantes en $O$.

e) Conclure.

Exercice 36

Le plan est rapporté au repère $(O\;,\ \vec{i}\\;,\ \vec{j})$

Soient $(O'\;,\ \vec{i'}\;,\ \vec{j'})$ tels que :

$\overrightarrow{OO'}=4\vec{i}+\vec{j}\;,\qquad\vec{i'}=3\vec{i}-2\vec{j}\;,\qquad\vec{j'}=\vec{i}+2\vec{j}$

1) Démontrer que $(O\;,\ \vec{i'}\;,\ \vec{j'})$ est un repère du plan.

2) Soit $M$ de coordonnées $(x\;,\ y)$ dans le premier repère, $(x'\;,\ y')$ dans le second repère.

Calculer $x'\text{ et }y'$ en fonction de $x\text{ et }y$.

Exercice 37

Soient $A\;,\ B\;,\ C$ trois points non alignés du plan.

On considère les repères $\mathcal{R}=(A\;,\ \overrightarrow{AB}\;,\ \overrightarrow{AC})\text{ et }\mathcal{R'}=(B\;,\ \overrightarrow{BA}\;,\ \overrightarrow{BC})$

Un point $M$ a pour coordonnées $(x\;,\ y)$ dans $\mathcal{R}$ et $(x'\;,\ y')$ dans $\mathcal{R'}$.

Exprimer $x\text{ et }y$ en fonction de $x'\text{ et }y'$.

Déterminer l'ensemble des points du plan qui ont les mêmes coordonnées dans les deux repères.

Exercice 38

Familles de droites

A) Déterminer suivant les valeurs du paramètre réel $a$, le nombre de solutions de l'équation :

$(a-2)x^{2}+2(a-1)x+a+4=0$, $x$ étant l'inconnue réelle.

B) Le plan est rapporté au repère $(O\;,\ \vec{i}\;,\ \vec{j})$

On considère l'ensemble $\mathcal{D}$ des droites $(d_{m})$ d'équations :

$(d_{m})\ :\ (m^{2}+m-2)x-(m+3)y-(m^{2}-5)=0$, $m$ étant un paramètre réel, et l'ensemble $\Delta$ des droites $(\delta_{a})$ d'équations :

$(\delta_{a})\ :\ ax+(a-2)y-6(a-1)=0$, $a$ étant un paramètre réel.

1) a) Déterminer et construire les droites de $\mathcal{D}$ parallèles aux axes.

b) Démontrer que toutes les droites de $\mathcal{D}$ passent par un point fixe $A$ que l'on déterminera.

2) a) Déterminer et construire les droites de $\Delta$ parallèles aux axes.

b) Démontrer que toutes les droites de $\Delta$ passent par un point fixe $C$ que l'on déterminera.

c) Discuter suivant la position d'un point $M_{0}(x_{0}\;,\ y_{0})$ dans le plan, le nombre de droites de $\Delta$ passant par $M_{0}$.

En déduire que l'ensemble des droites $\Delta$ est l'ensemble des droites passant par $C$ privé d'une droite que l'on précisera.

3) En prenant $a$ pour paramètre réel et $m$ pour inconnue, discuter suivant les valeurs de $a$ l'existence de droites $(d_{m})$ parallèles à une droite $(\delta_{a})$ donnée.

En déduire que l'ensemble $\mathcal{D}$ ne représente qu'une partie des droites passant par $A$.

4) Pour quelles valeurs de $a$ et $m$ les droites $(d_{m})\text{ et }(\delta_{a})$ sont-elles confondues ?

5) Les droites $(d_{1})\text{ et }(\delta_{2})$ se coupent en $B$.

Les droites $(\delta_{0})\text{ et }(\delta_{3})$ se coupent en $D$.

Quelle est la nature du quadrilatère $ABCD$ ?

Exercice 39

Notion de polaire

$ABC$ est un triangle et $J$ un point du segment $[BC]$.

Pour la suite, on utilisera le repère cartésien $(A\;,\ \overrightarrow{AB}\;,\ \overrightarrow{AC})$

1) Quelles sont les coordonnées de $B\text{ et }C$ ?

2) $(Bu)\;,\ (Cv)\;,\ (AJ)$ sont des droites de coefficients respectifs $a\;,\ a'\;,\ \alpha$.

De plus, $(Bu)$ coupe $(AC)\text{ en }P$ ; $(Cv)\text{ coupe }(AB)\text{ en }Q$, les droites $(Bu)\text{ et }(Cv)$ se coupent sur la droite $(AJ)$ au point $K$ distinct de $A$.

a) Déterminer les coordonnées des points $P\;,\ Q\text{ et }K$ en fonction de $a\text{ et }a'$.

b) Montrer que $a(1+a')=\alpha(1+a)$.

3) a) Déterminer les coordonnées du point d'intersection $O$ (lorsqu'il existe) des droites $(BC)\text{ et }(PQ)$.

b) Montrer que ces coordonnées sont indépendantes des réels $a\text{ et }a'$.

Que peut-on en déduire ?

4) Démontrer que
$$\dfrac{\overline{CO}}{\overline{CJ}}=-\dfrac{\overline{BO}}{\overline{BJ}}$$

La droite $(AJ)$ est appelée la polaire du point $O$ par rapport aux droites $(AB)\text{ et  }(AC)$.

5) $\Delta\text{ et }\Delta'$ sont des droites sécantes en $A$.

$O$ est un point qui n'appartient pas à $\Delta\text{ et }\Delta'$.

Construire la polaire du point $O$ par rapport aux droites $\Delta\text{ et }\Delta'$.

---