Série d'exercices sur la géométrie dans l'espace 1e S

Exercice 1

Soient deux plans distincts $\mathcal{P}\text{ et }\mathcal{P'}$, ayant au moins un point commun $A$.

Le plan $\mathcal{P}$ définit deux demi-espaces $\mathcal{E}_{1}\text{ et }\mathcal{E}_{2}.$

Soit $\mathcal{D'}$ une droite de $\mathcal{P'}$ coupant $P\text{ en } A\;,\ B$ un point de $\mathcal{D'}$ dans $\mathcal{E}_{1}$, $C$ un pont de $D'$ dans $\mathcal{E}_{2}.$

Soit $D$ un point de $\mathcal{P'}$ n'appartenant pas à $\mathcal{D'}$.

1) Si $D$ appartient à $\mathcal{P}$, que peut-on dire de l'intersection de $\mathcal{P}\text{ et }\mathcal{P'}$ ?

2) Si $D$ n'appartient pas à $\mathcal{P}$, $D$ appartient à l'un des demi-espaces,  par exemple.

Qu'en résulte-t-il pour le segment $[CD]$ ?

3) Déduire des questions 1) et 2) que deux plans distincts ayant au moins un point commun sont sécants.

Exercice 2

Soit un quadrilatère plan $ABCD$, tel que $(AB)\text{ et }(DC)\;,\ (AD)\text{ et }(BC)\;,\ (AC)\text{ et }(BD)$ soient sécants respectivement en $I\;,\ J\text{ et }K$.

Soit $S$ un point non situé dans le plan de $ABCD$.

On trace les droites $(SA)\;,\ (SB)\;,\ (SC)\text{ et }(SD)$.

1) Combien ces droites, associées deux à deux, déterminent-elles de plans ?

2) Construire les intersections de ces plans pris deux à deux.

Exercice 3

On donne deux droites sécantes $D\text{ et }D'$, deux points $A\text{ et }B\text{ de }D$, deux points $A'\text{ et }B'\text{ de }D'$.

Démontrer que les droites $(AB')\text{ et }(BA')$ sont sécantes ou parallèles.

Exerecice 4

Soit une droite $\mathcal{D}$ sécante à un plan $\mathcal{P}\text{ en }O$, et un point $A$ non situé sur $\mathcal{D}$ et sur $\mathcal{P}$

Un point $M$ décrit la droite $\mathcal{D}$ et la droite $(AM)$ coupe en général $\mathcal{P}$ en un point $I.$

1) Quel est l'ensemble des droites $(AM)$ ?

Démontrer que tous les points $I$ appartiennent à une droite fixée $\Delta$.

2) Tout point de $\Delta$ est-il un point $I$ ?

Exercice 5

Soit, dans un plan $\mathcal{P}$, deux droites $\mathcal{D}\text{ et }\mathcal{D'}$ sécantes en $O$.

Une droite $\Delta$ est sécante à $\mathcal{P}\text{ en }A\;,\ A$ n'appartenant pas à $\mathcal{D}\cup \mathcal{D'}$.

Soit $M$ un point de $\Delta$ distinct de $A.$

1) Déterminer l'intersection $\Delta'$ des plans $(M\;,\ \mathcal{D})\text{ et }(M\;,\ \mathcal{D'})$.

2) Lorsque $M$ décrit $\Delta$, démontrer que toutes les droites $\Delta'$ sont incluses dans un plan fixe.

Exercice 6

Soit un tétraèdre $ABCD\text{ et }\beta\;,\ \gamma\;,\ \delta$ les milieux respectifs de $[CD]\;,\ [DB]\;,\ [BC] $

1) Démontrer que $(BC)$ n'est pas dans le plan $(AD\delta).$

2) Démontrer que les trois plans $(AD\delta)\;,\ (AB\beta)\;,\ (AC\gamma)$ ont une droite commune que l'on précisera.

Exercice 7

Démontrer que trois droites, deux à deux sécantes, et non coplanaires ont un point commun.

Application :

Soit un tétraèdre $ABCD\;,\ A'\;,\ B'\;,\ C'\;,\ D'$ les centres de gravité des triangles $BCD\;,\ CDA\;,\ DAB\;,\ ABC.$

1) Soit $\beta$ le milieu de $[DC].$

Démontrer que $(AA')\;,\ (BB')$ sont dans le plan $(AB\beta)$.

2) En déduire que $(AA')\text{ et }(BB')$ sont concourantes en un point $G.$

3) Démontrer que $(AA')\;,\ (BB')\;,\ (CC')\text{ et }(DD')$ sont concourantes en $G.$

Exercice 8

On donne trois points non alignés $A\;,\ B\text{ et }C.$

Soit $D$ un point de la droite $(AB)\text{ et }E$ un point de la droite $(AC).$

Démontrer que les droites $(BC)\text{ et }(DE)$ sont sécantes ou parallèles.

Exercice 9

Soient dans un plan $P$ deux points $B\text{ et }C.$

Soit $D$ un point n'appartenant pas au plan $P.$

1) Démontrer que les points $B\;,\ C\;,\ D$ ne sont pas alignés ; en déduire qu'ils déterminent un plan.

2) Soit $E$ un point du plan $(BCD)$.

On suppose que la droite $(DE)$ coupe le plan $P\text{ en }F.$

Démontrer que les points $B\;,\ C\;,\ F$ sont alignés.

Exercice 10

Soit un tétraèdre $ABCD$ et trois points $M\;,\ N\;,\ P$, appartenant respectivement aux arêtes $(AB)\;,\ (AC)\;,\ (AD)$ de ce tétraèdre.

On suppose que les droites $(MN)\;,\ (NP)\;,\ (MP)$ percent le plan $(BCD)$ respectivement en $P'\;,\ M'\;,\ N'.$

Démontrer que que les points $M'\;,\ N'\;,\ P'$ appartiennent à la fois au plan $(MNP)$ et au plan $(BCD).$

En déduire que $M'\;,\ N'\;,\ P'$ sont alignés.

Exercice 11

Soit un plan $\mathcal{P}$, $A\text{ et }B$ deux points distincts non situés dans $\mathcal{P}.$

La droite $(AB)$ perce $\mathcal{P}\text{ en }I$.

Soit $M$ un point de l'espace distinct de $A\text{ et }B$, et $A'\text{ et }B'$ les points d'intersection de $\mathcal{P}$ et des droites $(MA)\text{ et }(MB)$ lorsqu'ils existent.

Démontrer que $A'\;,\ B'\text{ et }I$ sont alignés.

Exercice 12

Soit $Ox\;,\ Oy\;,\ Oz$ trois demi-droites concourantes non coplanaires.

On marque deux points $A\text{ et }A'$ sur $Ox\;,\ B\text{ et }B'\text{ sur }Oy\;,\ C\text{ et }C'\text{ sur }Oz.$

1) Démontrer qu'en général les droites $(BC)\text{ et }(B'C')\;,\ (CA)\text{ et }(C'A')\;,\ (AB)\text{ et }(A'B')$ se coupent respectivement en $\alpha\;,\ \beta\;,\ \gamma$.

2) Dans le cas où $\alpha\;,\ \beta\;,\ \gamma$ existent, démontrer que ces points sont alignés.

Exercice 13

Deux plans distincts $\mathcal{P}\text{ et }\mathcal{Q}$ se coupent suivant la droite $\mathcal{D}_{1}.$

Soit $\mathcal{D}_{2}$ une droite de $\mathcal{P}$ non parallèle à $\mathcal{D}_{1}\text{ et }A$ un point de $\mathcal{Q}$ non situé sur $\mathcal{D}_{1}.$

Démontrer que le plan $(A\;,\ \mathcal{D}_{2})$ coupe $\mathcal{Q}$ suivant une droite $\mathcal{D}_{3}$ concourante avec $\mathcal{D}_{1}\text{ et }\mathcal{D}_{2}.$

Exercice 14

Deux plans $\mathcal{P}\text{ et }\mathcal{Q}$ se coupent suivant la droite $\mathcal{D}$.

Soit $A$ un point de $\mathcal{P}$ et une droite $(BC)\text{ de }\mathcal{Q}.$

Déterminer l'intersection des plans $(ABC)\text{ et }\mathcal{P}.$

Exercice 15

Dans le cube ci-dessous, les points $I\;,\ J\;,\ K\;,\ L\;,\ M\;,\ P$ sont des milieux d'arêtes.

Dans chaque cas, préciser la position respective des deux droites :

a) $(AK)\text{ et }(BG)\;;$

b) $(IJ)\text{ et }(BG)\;;$

c) $(IP)\text{ et }(LM).$

Sont-elles strictement parallèles ?

Sont-elles sécantes ?

Sont-elles coplanaires ?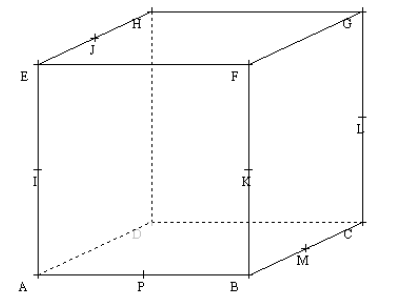

Exercice 16

On considère un cube.

Les points indiqués sont les sommets et les milieux de certaines arêtes

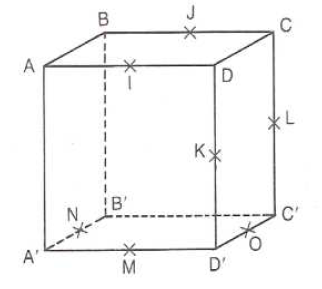
Dire si les droites suivantes sont sécantes, parallèles ou non coplanaires :

$a)\ (IJ)\text{ et }(D'C')\;;\qquad b)\ (MK)\text{ et }(B'C)$

$c)\ (AB)\text{ et }(KC)\qquad d)\ (AJ)\text{ et }(KC)$

$e)\ (A'I)\text{ et }(B'J)\;;\qquad f)\ (MD)\text{ et }(B'J)\;;\qquad g)\ (AM)\text{ et }(CO).$

Exercice 17

Configuration de Desargues

Soient trois droites non coplanaires $D_{1}\;,\ D_{2}\text{ et }D_{3}$ concourantes en $O$.

Soient deux points $A\text{ et }A'\text{ de }D_{1}$, deux points $B\text{ et }B'\text{ de }D_{2}$, deux points $C\text{ et }C'\text{ de }D_{3}.$

1) Démontrer que les droites $(AB)\text{ et }(A'B')$ sont coplanaires.

Établir des résultats analogues pour les droites $(BC)\text{ et }(B'C')$, pour les droites $(CA)\text{ et } (C'A').$

2) On suppose que les droites $(BC)\text{ et }(B'C')$ se coupent en $A_{1}$, que les droites $(CA)\text{ et }(C'A')$ se coupent en $B_{1}$, que les droites $(AB)\text{ et }(A'B')$ se coupent en $C_{1}.$

Démontrer que les points $A_{1}\;,\ B_{1}\text{ et }C_{1}$ sont alignés.

Exercice 18

Configuration des triangles homologiques

Soient $P\text{ et }Q$ deux plans sécants et $D$ leur droite d'intersection.

Soient $ABC\text{ et }A'B'C'$ deux triangles respectivement contenus dans les plans $P\text{ et }Q.$

On suppose que les triangles $ABC\text{ et }A'B'C'$ sont tels que $(BC)\text{ et }(B'C')$ se coupent en $A_{1}\;,\ (CA)\text{ et }(C'A')$ se coupent en $B_{1}\;,\ (AB)\text{ et }(A'B')$ se coupent en $C_{1}.$

(Deux triangles vérifiant ces propriétés sont dits homologiques).

1) Établir que $A_{1}\;,\ B_{1}\text{ et }C_{1}$ sont alignés et préciser la droite contenant $A_{1}\;,\ B_{1}\text{ et }C_{1}.$

2) On suppose que les droites $(BB')\text{ et }(CC')$ sont sécantes en $O.$

Démontrer que le point $O$ appartient au plan $(ACA')$ et au plan $(ABA')$ ;

en déduire que $O$ appartient à la droite $(AA')$, donc que les droites $(AA')\;,\ (BB')\text{ et }(CC')$ sont concourantes.

Exercice 19

On donne un plan $\mathcal{P}$ et une droite $\mathcal{D}$ non parallèle à $\mathcal{P}$.

A chaque plan $\mathcal{Q}$ non parallèle à $\mathcal{P}$, on associe la droite $\mathcal{D'}$, intersection du plan

$\mathcal{Q}$ et du plan $\mathcal{P}$.

Démontrer que toutes les droites $\mathcal{D'}$ passent par un point fixe.

Exercice 20

Soit un plan $\mathcal{P}$ et trois points $A\;,\ B\;,\ C$ non alignés et n'appartenant pas à $\mathcal{P}$.

On suppose que les droites $(BC)\;,\ (CA)\text{ et }(AB)$ percent respectivement le plan en $A'\;,\ B'\text{ et }C'.$

1) Démontrer que $A'\;,\ B'\;,\ C'$ sont alignés.

2) Soit $M$ un point de l'espace tel que les droites $(MA)\;,\ (MB)\;,\ (MC)$ percent respectivement $\mathcal{P}\text{ en }A_{1}\;,\ B_{1}\text{ et }C_{1}.$

Démontrer que les droites $(A_{1}B_{1})\;,\ (B_{1}C_{1})\;,\ (C_{1}A_{1})$ passent chacune par un point qui ne dépend pas du point $M$ choisi.

Exercice 21

Soit un tétraèdre $ABCD$ ; $E\;,\ F\text{ et }G$ trois points pris respectivement sur $]AB[\;,\ ]AC[\text{ et }]BD[.$

On suppose que $(EF)$ n'est pas parallèle à $(BC)$ et que $(FG)$ n'est pas parallèle à $(CD)$.

Construire :

1) l'intersection des plans $(EFG)\text{ et }(BCD)$ ;

2) l'intersection de chacune des droites $(AD)\text{ et }(CD)$ avec le plan $(EFG).$

Exercice 22

Soit un tétraèdre $ABCD.$

Une droite $\Delta$ du plan $(BCD)$ rencontre les cotés du triangle $BCD$ en trois points distincts $D'\;,\ B'\;,\ C'.$

Soit $I$ un point de $]AC[\;;\ I$ détermine avec $\Delta$ un plan $\mathcal{P}.$

1) Dessiner l'intersection de $\mathcal{P}$ et du plan $(ABC)$, puis l'intersection de $\mathcal{P}$ et du plan $(ACD).$

2) Construire les points d'intersection de $(AB)\text{ et }(AD)$ avec $\mathcal{P}$, en déduire l'intersection des plans $\mathcal{P}\text{ et }(ABD).$

Exercice 23

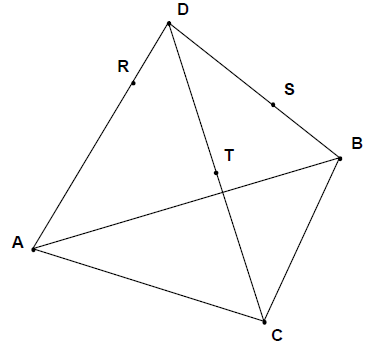
Les trois points $A\;,\ B\text{ et }C$ déterminent un plan $\mathcal{P}.$

Le point $D$ n'appartient pas à $\mathcal{P}.$

Le point $R$ appartient à $[AD]$ ; le point $S$ appartient à $[BD]$ ; le point $T$ appartient à $[CD].$

Dessiner l'intersection du plan contenant $R\;,\ S\;,\text{ et }T$ avec le plan $\mathcal{P}$ et expliquer la construction en indiquant les théorèmes que l'on a utilisés

Exercice 24

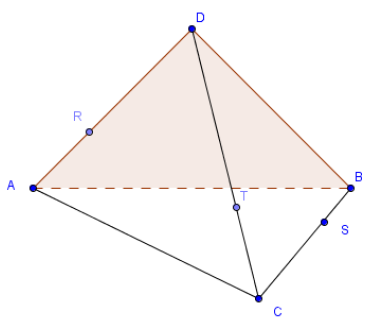
Les 3 points $A\;,\ B\text{ et }C$ déterminent un plan $\mathcal{P}.$

Le point $D$ n'appartient pas à $\mathcal{P}.$

Le point $R$ appartient à $[AD]$ ; le point $S$ appartient à $[BC]$ ; le point $T$ appartient à $[CD]$.

a) Dessiner l'intersection du plan contenant $R\;,\ S\text{ et }T$ avec le plan $\mathcal{P}.$

b) Dessiner l'intersection du plan contenant $R\;,\ S\text{ et }T$ avec le plan contenant $A\;,\ B\text{ et }D.$

c) Tracer en couleur l'intersection du plan contenant $R\;,\ S\text{ et }T$ avec le tétraèdre $ABCD$, c'est-à-dire avec chacun des triangles $ABC\;,\ DAB\;,\ DAC\text{ et }DBC$

Parallélisme

Exercice 25

Soit un tétraèdre $ABCD.$

On désigne par $I\;,\ J\;,\ K\;,\ L$ les milieux respectifs des segments $[AB]\;,\ [CD]\;,\ [BC]\;,\ [AD].$

1) En raisonnant dans le plan $(BCD)$, établir que les droites $(JK)\text{ et }(BD)$ sont parallèles.

2) Démontrer que les droites $(JK)\text{ et }(IL)$ sont parallèles, ainsi que les droites $(IK)\text{ et }(LJ).$

3) Démontrer que $I\;,\ J\;,\ K\;,\ L$ sont coplanaires, et préciser la nature du quadrilatère $IJKL.$

4) Démontrer que les segments $[IJ]\text{ et }[KL]$ ont le même milieu noté $O.$

5) Soient $M\text{ et }N$ les milieux respectifs des segments $[AC]\text{ et }[BD].$

Démontrer que $O$ est le milieu de $[MN].$

Exercice 26

On donne deux droites parallèles distinctes $D\text{ et }D'.$

Soit $O$ un point n'appartenant pas au plan déterminé par les droites $D\text{ et }D'.$

On désigne par $P$ le plan contenant le point $O$ et la droite $D$, par $P'$ le plan contenant le point $O$ et la droite $D'$.

Démontrer que la droite d'intersection des plans $P\text{ et }P'$ est parallèle à $D$ et à $D'.$

Exercice 27

Soit un tétraèdre $ABCD$ et $M$ un point de l'arête $[AD]$.

On désigne par $Q$ le plan contenant $M$ et parallèle aux droites $(AB)\text{ et }(CD).$

Étudier la nature de l'intersection du plan $Q$ et du tétraèdre $ABCD.$

Exercice 28

On considère le tétraèdre $ABCD.$

$I$ appartient à $[AB]$.

$J$ appartient au plan $ABC.$

$K$ appartient au plan $ACD.$

$L$ appartient au plan $ABD.$

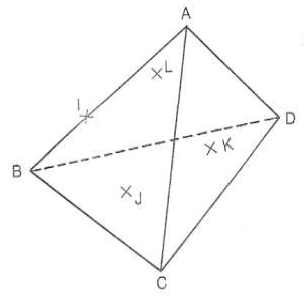
1) Déterminer l'intersection de la droite $(IJ)$ et du plan $BCD$

2) On veut déterminer l'intersection de la droite $(IK)$ et du plan $BCD.$

Soit $M$ un point de $(AC)$.

Déterminer l'intersection des plans $IMK\text{ et }BCD$

Déterminer l'intersection de $(IK)$ et du plan $BCD$

3) a) Construire la parallèle à $(CD)$ passant par $K$

b) Construire la parallèle à $(BD)$ passant par $K$ et déterminer son intersection avec le plan $ABC.$

Exercice 29

Deux plans $P\text{ et }P'$ sécants suivant une droite $\Delta$ sont parallèles à une droite $D$.

Soit $D'$ la parallèle à $D$ passant par un point $A\text{ de }\Delta$.

1) Démontrer que $D'\subset P$ et que $D'\subset P'.$ En déduire que $D'=\Delta$.

2) Conclure par une propriété.

Exercice 30

Soit un tétraèdre $ABCD\text{ et }M$ un point de $]A\;,\ B[$.

On mène par $M$ le plan parallèle à $(AC)\text{ et }(BD)$, qui coupe $(BC)\text{ en }N$, $(CD)\text{ en }P$, $(DA)\text{ en }Q.$

Démontrer que $MNPQ$ est un parallélogramme.

Exercice 31

On donne deux plans strictement parallèles $P\text{ et }P'.$

Soit trois points non alignés $A\;,\ B\;,\ C\text{ de }P$ et trois points non alignés $A'\;,\ B'\;,\ C'\text{ de }P'.$ tels que les droites $(BC)\text{ et }(B'C')$ ne soient pas parallèles.

Construire l'intersection des plans $(AB'C')\text{ et }(A'BC)$.

Exercice 32

Soient $D\text{ et }D'$ deux droites strictement parallèles et $A$ un point n'appartenant pas au plan déterminé par $D\text{ et }D'.$

Quelle est l'intersection des plans $(A\;,\ D)\text{ et }(A\;,\ D')$ ?

Exercice 33

Soit un plan $P$ et une droite $(AB)$ strictement parallèle à $P$.

$M\text{ et }N$ étant deux points de $P$, que peut-on dire des droites d'intersection $\Delta\text{ et }\Delta'$ des plans $(ABM)\text{ et }(ABN)\text{ avec }P$ ? Peut-on avoir $\Delta=\Delta'$ ?

Exercice 34

Soient $P\text{ et }P'$ deux plans parallèles. Une droite $D$ perce $P\text{ en }A\text{ et }P'\text{ en }A'.$

Soit une droite $\Delta$, parallèle à $D$.

1) Démontrer que $\Delta$ perce $P\text{ et }P'\text{ en }B\text{ et }B'.$

2) Que peut-on dire du quadrilatère $ABB'A'$ ?

Exercice 35

Soit dans un plan $P$ un parallélogramme $ABCD$ et soit $S$ un point non situé dans $P.$

Un plan $P'$ parallèle à $P\text{ coupe }(SA)\text{ en }A'\;,\ (SB)\text{ en }B'\;,\ (SC)\text{ en }C'\text{ et }(SD)\text{ en }D'.$

Démontrer que $A'B'C'D'$ est un parallélogramme.

Projections

Exercice 36

On donne un plan $P$ et une droite $D$ non parallèle à $P.$

Soient $D_{1}\text{ et }D_{2}$ deux droites.

On suppose que les projetées des droites $D_{1}\text{ et }D_{2}$ sur le plan parallèlement à la droite $D$ sont deux droites distinctes $D'_{1}\text{ et }D'_{2}.$

1) On suppose que $D_{1}\text{ et }D_{2}$ sont sécantes.

Démontrer que $D'_{1}\text{ et }D'_{2}$ sont sécantes.

Quelle est l'intersection des droites $D'_{1}\text{ et }D'_{2}$ ?

2) On suppose que $D'_{1}\text{ et }D'_{2}$ sont sécantes :

peut-on en déduire que $D_{1}\text{ et }D_{2}$ sont sécantes ?

Exercice 37

Trois points alignés peuvent-ils se projeter dans un plan suivant trois points alignés ? Si oui, préciser dans quel cas.

Exercice 38

Soient deux droites non coplanaires $D_{1}\text{ et }D_{2}$ qui percent un plan $P$ en deux points $A_{1}\text{ et }A_{2}.$

A chaque point $M_{1}\text{ de }D_{1}$ on associe le plan $Q$ contenant $M_{1}$ et parallèle à $P$.

On désigne par $M_{2}$ l'intersection du plan $Q$ et de $D_{2}$ et par $M$ le projeté de $M_{2}$ dans $P$ parallèlement à $D_{1}$.

1) Comparer les distances $M_{1}M_{2}\text{ et }A_{1}M$.

2) Démontrer que lorsque $M_{1}$ varie sur $D_{1}$ le point $M$ appartient à une droite fixe.

3) Déterminer le point $M_{1}$ pour que la distance $M_{1}M_{2}$ soit la plus courte possible.

Exercice 39

Soient deux droites $D\text{ et }D'$ non coplanaires et un plan $P$.

Déterminer la direction $\Delta$ de projection pour que $D\text{ et }D'$ se projettent suivant deux droites parallèles.

Exercice 40

Soit un plan $P$, une droite $\Delta$ et un parallélogramme $ABCD$ situé dans un plan $P$ non parallèle à $\Delta$.

Montrer que la projection de $ABCD$ sur $P$ parallèlement à $\Delta$ est un parallélogramme.

Exercice 41

Un quadrilatère plan $ABCD$ se projette sur un plan $P$ suivant un parallélogramme $A'B'C'D'$.

Déterminer la nature de $ABCD$.

Exercice 42

Trouver un plan $P$ et une droite $\Delta$ tels qu'un quadrilatère gauche donné $ABCD$ se projette sur $P$ parallèlement à $\Delta$ suivant un parallélogramme.

Exercice 43

Soit $A'B'C'$ la projection sur un plan $P$ parallèlement à une droite $\Delta$ d'un triangle $ABC$ situé dans un plan non parallèle à $\Delta$.

Montrer que les milieux des cotés de $A'B'C'$ sont les projections des milieux des cotés de $ABC$ et que le centre de gravité de $A'B'C'$ est la projection du centre de gravité de $ABC.$

Exercice 44

Soit un tétraèdre $ABCD$, $I$ le milieu de $[AB]\text{ et }J$ le milieu de $[CD]$.

1) Construire la projection du tétraèdre sur le plan $BCD$ parallèlement à la droite $(IJ)$.

2) Quelle est la nature de la figure obtenue ?

3) La figure peut-elle être un carré ; à quelles conditions ?

Exercice 45

Soit un cube $ABCDA'B'C'D'$.

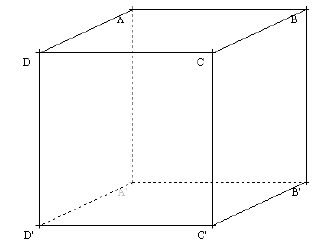
1) Construire l'image du cube par la projection sur le plan $A'B'C'$ parallèlement à la droite $(AA')$.

2) Construire l'image du cube par la projection sur le plan $A'B'C'$ parallèlement à la droite $(AD')$.

3) Construire l'image du cube par la projection sur le plan $A'B'C'$ parallèlement à la droite $(AC')$.

Problèmes de construction

Exercice 46

Soient deux droites strictement parallèles $D\text{ et }D'$ et deux droites quelconques $\Delta\text{ et } \Delta'$ sécantes avec le plan déterminé par $D\text{ et }D'$.

Si une droite $(x'x)$ rencontre $D\text{ et }D'$, dans quel plan se trouve-telle ?

Construire une droite rencontrant $D\;,\ D'\;,\ \Delta\text{ et }\Delta'$. Est-ce toujours possible ?

Exercice 47

Soit une droite $D$ et une droite $\delta$ non parallèle à $D$.

1) Démontrer que toutes les droites $\Delta$ parallèles à $\delta$ et sécantes à $D$ sont dans un même plan $P$.

2) Soit $D'$ une droite non coplanaire avec $D$ et sécante avec $P$.

Construire une droite $\Delta$ parallèle à $\delta$ et sécante à $D\text{ et }D'$.

Exercice 48

Soit deux droites non coplanaires $D\text{ et }D'\text{ et }A$ un point n'appartenant ni à $D$ ni à $D'.$

Dans quel cas peut-on mener par $A$ une droite parallèle à $D$ et sécante à $D'$ ?

Exercice 49

On donne un plan $P$, une droite $D$ sécante avec $P$, et un point $A$ n'appartenant ni à $D$ ni à $P$.

Construire une droite $\Delta$ passant par $A$ rencontrant $D$ et parallèle à $P$.

Vecteurs et repères

Dans les exercices 50 à 52, on considère un tétraèdre $ABCD$ (voir figure ci-dessous)

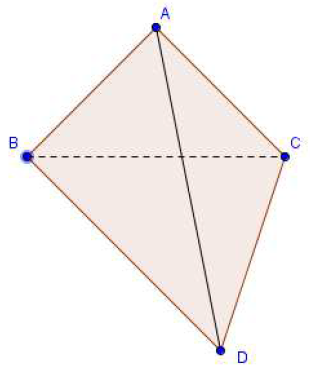
Exercice 50

1) Construire les représentants d'origine $A$ des vecteurs :

$a)\ \overrightarrow{AB}+\overrightarrow{CD}\qquad b)\ \overrightarrow{AC}+\overrightarrow{BA}+\overrightarrow{DA}$

$c)\ \overrightarrow{BD}+\overrightarrow{AB}+\overrightarrow{DA}\qquad d)\ \overrightarrow{BC}-2\overrightarrow{CD}-\overrightarrow{DB}$

Exercice 51

Soit $k$ un réel non nul et $\alpha\;,\ \beta\;,\ \gamma\text{ et }\delta$ les points définis par :
$$\overrightarrow{A\alpha}=k\overrightarrow{AB}\;,\ \overrightarrow{A\beta}=k\overrightarrow{AC}\;;\ \overrightarrow{D\gamma}=k\overrightarrow{DC}\;,\ \overrightarrow{D\delta}=k\overrightarrow{DB}$$

Démontrer que $\alpha\beta\gamma\delta$ est un parallélogramme.

Exercice 52

Soit $A'\;,\ B'\;,\ C'\text{ et }D'$ les centres de gravité des triangles $BCD\;,\ ACD\;,\ ABD\text{ et }ABC$.

1) Montrer que $\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}=3\overrightarrow{AA'}$

2) Simplifier la somme :

$\overrightarrow{AA'}+\overrightarrow{BB'}+\overrightarrow{CC'}+\overrightarrow{DD'}$

3) Soit $M$ un point quelconque, montrer que :

$$\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}=\overrightarrow{MA'}+\overrightarrow{MB'}+\overrightarrow{MC'}+\overrightarrow{MD'}$$

Exercice 53

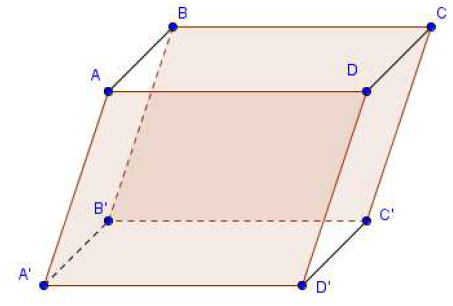
On considère le parallélépipède $ABCDA'B'C'D'$ ci-dessous.

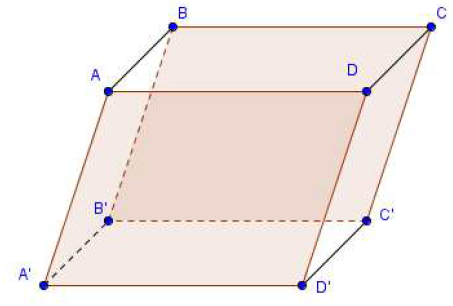
Construire un représentant d'origine $A$ des vecteurs suivants :

$a)\quad\overrightarrow{A'B'}+\overrightarrow{AD}+\overrightarrow{C'D'}$ $b)\quad\dfrac{1}{2}\overrightarrow{A'D'}+\dfrac{1}{2}\overrightarrow{AD'}$

$c)\quad\dfrac{1}{2}\overrightarrow{AC'}+\dfrac{1}{2}\overrightarrow{B'D}$

Exercice 54

On considère toujours le parallélépipède $ABCDA'B'C'D'$ de l'exercice 52.

1) Construire l'isobarycentre $G$ du parallélépipède.

2) Calculer $\overrightarrow{GA}+\overrightarrow{GC'}$

3) Montrer que $G$ est centre de symétrie du parallélépipède.

4) Construire les isobarycentres

$I\text{ de }A\;,\ B\;,\ B'\;,\ A'\;;\ J\text{ de }D\;,\ C\;,\ D'\;,\ C'\;;\ K\text{ de }A\;,\ B\;,\ C\;,\ D\;;\ L\text{ de }A'\;,\ B'\;,\ C'\;,\ D'.$

5) Montrer que les droites $(IJ)\text{ et }(KL)$ sont concourantes.

6) Quelle est la nature du quadrilatère $IKJL$ ?

Exercice 55

On considère encore le parallélépipède $ABCDA'B'C'D'$ de l'exercice 52.

Soit $I$ le point défini par :

$\overrightarrow{AI}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{BD}$

Soit $J$ le point défini par :$\overrightarrow{A'J}=\overrightarrow{A'C}+\overrightarrow{BD'}$

1) Montrer que $A\;,\ A'\;,\ I\text{ et }J$ sont coplanaires.

2) Quelle est la nature du quadrilatère $AA'JI$ ?

Exercice 56

Soit un tétraèdre $ABCD$.

Quelles sont dans le repère $(A\;;\ \overrightarrow{AB}\;,\ \overrightarrow{AC}\;,\ \overrightarrow{AD})$ les coordonnées des sommets du tétraèdre, des centres de gravité des faces du tétraèdre, et les coordonnées de l'isobarycentre des quatre points $A\;,\ B\;,\ C\text{ et }D.$

Exercice 57

Soit un parallélépipède $ABCDA'B'C'D'$ ($ABCD$ est un parallélogramme et on a $\overrightarrow{AA'}=\overrightarrow{BB'}=\overrightarrow{CC'}=\overrightarrow{DD'}$

Quelles sont, dans le repère $(A\;;\ \overrightarrow{AB}\;,\ \overrightarrow{AD}\;,\ \overrightarrow{AA'})$ les coordonnées des sommets de ce parallélépipède, des centres des six faces et du centre du parallélépipède ?

Exercice 58

L'espace est muni du repère $(O\;;\ \vec{i}\;,\ \vec{j}\;,\ \vec{k}$.

On considère les points $A(1\;,\ 2\;,\ 3)\;,\ B(-1\;,\ 3\;,\ 3)\text{ et }C(-2\;,\ 1\;,\ 4)$.

1) a) Existe-t-il des points d'abscisse 3 alignés avec $A\text{ et }B$ ?

b) Existe-t-il des points d'ordonnée 5 alignés avec $A\text{ et }B$ ?

c) Déterminer deux points coplanaires avec $A\;,\ B\text{ et }C$.

d) Déterminer un point d'abscisse 0 et d'ordonnée 1 coplanaire avec $A\;,\ B\text{ et }C$.

2) a) Les vecteurs $\overrightarrow{AB}\;,\ \overrightarrow{AC}\text{ et }\overrightarrow{BC}$ définissent-ils une base de l'ensemble des vecteurs de l'espace ?

b) Les vecteurs $\overrightarrow{AB}\;,\ \overrightarrow{AC}\text{ et }\overrightarrow{AO}$ définissent-ils une base de l'ensemble des vecteurs de l'espace ?

Si oui, donner dans cette base les coordonnées des vecteurs $\overrightarrow{BC}\;,\ \overrightarrow{OB}\text{ et }\overrightarrow{CO}$

Exercice 59

Soient $A\;,\ B\;,\ C\text{ et }D$ quatre points non coplanaires et $E$ tel que $BDCE$ soit un parallélogramme.

Soient $B'\;,\ C'\text{ et }D'$ les milieux de $[AB]\;,\ [AC]\text{ et }[AD]$ et $I$ le milieu de $[BE]$.

1) a) Montrer que les droites $(EB)\text{ et }(C'D')$ sont parallèles.

b) Les droites $(BC')\text{ et }(ID')$ sont-elles sécantes ou non coplanaires ?

c) Que peut-on dire des plans $(B'C'D')\text{ et }(BCD)$ ?

d) On trace par $B'$ la droite parallèle à $(ED)$.

Déterminer son intersection avec le plan $(ACD)$.

2) On considère le plan $(A\;;\ \overrightarrow{AB}\;,\ \overrightarrow{AC}\;,\ \overrightarrow{AD})$

a) Donner les coordonnées des différents points de la figure.

b) Démontrer analytiquement les résultats du 1).

Exercice 60

On considère un cube (cf. figure ci-dessous)

1) Montrer que les vecteurs $\overrightarrow{AB}\;,\ \overrightarrow{AB}\text{ et }\overrightarrow{AB}$ définissent une base de l'ensemble des vecteurs du plan.

2) Donner dans le repère $(O\;;\ \overrightarrow{OA}\;,\ \overrightarrow{OC}\;,\ \overrightarrow{OO'})$ les coordonnées des points de la figure.

3) Donner un système d'équations paramétriques des droites $(A'I)\text{ et }(C'J)$ et étudier l'intersection de ces deux droites.

Retrouver le résultat géométriquement.

4) Déterminer un système d'équations paramétriques de la droite $(BB')$ et du plan $(AA'C)$.

5) Soit $M$ un point de $(BB')\text{ et }G$ l'isobarycentre de $O$, $A\text{ et }M$.

Montrer que $G$ appartient au plan $AA'C'$ (analytiquement puis géométriquement).

6) $M$ décrit la droite $(BB')$ ; quel est l'ensemble des points $G$ ? (On pourra démontrer le résultat géométriquement ou analytiquement).