Vous êtes ici

Série d'exercices : Droites remarquables 4e

Classe:

Quatrième

Exercice 1

1) Construire un triangle

$ABC$ quelconque.

2) a) Construire

$(b_{2})$ bissectrice de l'angle

$\widehat{A}$ ; elle coupe

$(BC)$ en

$A'.$

b) Construire la droite

$(b_{1})$ bissectrice de l'angle

$\widehat{B}$ ; elle coupe

$(AC)$ en

$B'.$

3) a)

$(b_{1})$ et

$(b_{2})$ se coupent en

$O$ , marque

$O.$

4) a) La droite perpendiculaire à

$(AB)$ et passant par

$O$ coupe la droite

$(AB)$ en

$I.$

b) La droite perpendiculaire à

$(BC)$ et passant par

$O$ coupe la droite

$(BC)$ en

$J.$

c) La perpendiculaire à

$(AC)$ et passant par

$O$ coupe la droite

$(AC)$ en

$K.$

5) a) Démontrer que :

$OI=OJ=OK.$

b) En déduire que

$(b_{3})$ bissectrice de

$\widehat{C}$ passe par

$O.$

c) Énoncer la propriété que tu viens de démontrer pour les bissectrices.

d) Que représente le point

$O$ pour le triangle

$ABC\ ?$

Exercice 2

Construire un triangle

$MNP$ tel que :

$MN=6\;cm\;;\ NP=5\;cm$ et

$MP=7\;cm.$

1) La bissectrice de l'angle

$\widehat{M}$ coupe

$[NP]$ en

$E.$

2) La bissectrice de l'angle

$\widehat{N}$ coupe

$(ME)$ en

$I.$

3) Démontrer que

$(IP)$ est la bissectrice de l'angle

$\widehat{MPN}.$

Exercice 3

$ABCD$ est un parallélogramme de centre

$O\;,\ P$ est le milieu de

$[OB].$

Les droites

$(CP)$ et

$(DA)$ se coupent en

$R.$

$T$ est le symétrique de

$R$ par rapport à

$P$

Les droites

$(RO)$ et

$(DT)$ se coupent en

$M.$

1) Faire une figure complète.

2) Montrer que

$(DP)$ est une médiane de

$RDT.$

3) Montrer que

$DO=\dfrac{2}{3}DP$

4) Quel est le centre de gravité du triangle

$RDT.$

5) Démontrer que

$M$ est milieu du segment

$[DT].$

Exercice 4

1) Construire un triangle

$ABC$ tel que :

$AB=5\;cm\;,\ AC=4\;cm$ et

$BC=6\;cm.$

$I$ et

$J$ sont les milieux respectifs de

$[AB]$ et

$[AC].$

2) Montrer que les droites

$(IJ)$ et

$(BC)$ sont parallèles puis calculer

$IJ.$

3) Les demi-droites

$[BJ)$ et

$[CI)$ se coupent en

$G.$

a) Que représentent les demi-droites

$[BJ)$ et

$[CI)$ pour le triangle

$ABC\ ?$

b) Que représente le point

$G$ pour le triangle

$ABC\ ?$

4) Soit

$K$ le milieu du segment

$[BC]$ . Montrer que les points

$A\;,\ G$ et

$K$ sont alignés.

5) On donne

$AK=3\;cm$ . Calculer

$AG$ et

$GK.$

Exercice 5

1) Construire un triangle

$ABC$ quelconque.

2) a) Construire la droite

$(m_{1})$ médiatrice de

$[AB].$

b) Construire la droite

$(m_{2})$ médiatrice de

$[BC].$

2) a) Les droites

$(m_{1})$ et

$(m_{2})$ se coupent en

$O.$

3) a) Démontrer que :

$OA=OB=OC.$

b) En déduire que la droite

$(m_{3})$ médiatrice de

$[AC]$ passe par

$O.$

c) Énoncer la propriété que tu viens de démontrer pour les médiatrices.

d) Que représente le point

$O$ pour le triangle

$ABC\ ?$

Exercice 6

1) Construire un triangle

$ABC$ quelconque.

2) a) Construire

$(AM)$ hauteur issue de

$A.$

b) Construire la droite

$(BN)$ hauteur issue de

$B.$

3) Les deux droites

$(AM)$ et

$(BN)$ se coupent en

$H$ , placer le point

$H.$

4) a) Construire la droite

$(B'C')$ passant par

$A$ et parallèle à

$(BC).$

b) Construire la droite

$(A'C')$ passant par

$B$ et parallèle à

$(AC).$

c) Construire la droite

$(B'A')$ passant par

$C$ et parallèle à

$(AB).$

5) Démontrer que : les quadrilatères

$ABCB'\;;\ BCAC'$ et

$CABA'$ sont des parallélogrammes.

6) a) Démontrer que

$(AH)$ est la médiatrice de

$[B'C'].$

b) Démontrer que

$(BH)$ est la médiatrice de

$[A'C'].$

c) Démontrer que

$(CH)$ est la troisième médiatrice du triangle

$A'B'C'.$

7) a) Que représentent les médiatrices du triangle

$A'B'C'\ ?$

b) Énoncer la propriété que tu viens de démontrer pour les hauteurs du triangle.

c) Que représente le point

$H$ pour le triangle

$ABC$

Exercice 7

Soit

$ABCD$ un parallélogramme de centre

$H.$ La perpendiculaire à

$(DB)$ passant par

$A$ et la La perpendiculaire à

$(AC)$ passant par

$B$ se coupent en

$G.$

1) Faire une figure.

2) Que représente le point

$H$ pour le triangle

$AGB.$

3) Montrer que les droites

$(GH)$ et

$(AB)$ sont perpendiculaires.

4) Montrer que les droites

$(GH)$ et

$(DC)$ sont perpendiculaires.

Exercice 8

Soit

$ABC$ un triangle tel que :

$AB=6\;cm\;;\ AC=7\;cm$ et

$BC=8\;cm.$

Les points

$L\;,\ M$ et

$N$ sont les milieux respectifs des côtés

$[BC]\;,\ [AB]$ et

$[AC]$ d'un triangle

$ABC.$

$G$ est le centre de gravité.

1) Faire une figure complète.

2) Démontrer que

$MLNA$ est un parallélogramme. Soit

$K$ sont centre.

En déduire que :

$AK=\dfrac{1}{2}AL$ puis

$KG=\dfrac{1}{6}AL$

Exercice 9

Soit

$ABCD$ un parallélogramme et

$E$ le symétrique de

$D$ par rapport à

$C.$ Les droites

$(AD)$ et

$(BE)$ se coupent en

$F.$

1) Montrer que

$B$ est le milieu du segment

$[EF].$

2) Montrer que

$A$ est le milieu du segment

$[DF].$

3) Les droites

$(FC)$ et

$(DB)$ se coupent en

$G.$ Démontrer que les points

$A\;,\ G$ et

$E$ sont alignés.

Exercice 10

1) Construis un triangle

$ABC$ tel que

$AB=14\;cm\;,\ AC=10\;cm\text{ et }BC=12\;cm.$

2) Construis ses médiatrices en rouge, ses médianes en vert, ses hauteurs en bleu et ses bissectrices en noir.

3) Place le point

$G$ centre de gravité du triangle, le point

$O$ centre du cercle circonscrit, le point

$I$ centre du cercle inscrit et le point

$H$ orthocentre du triangle.

4) Pour ce triangle

$ABC$ , construis les cercles circonscrit et inscrit.

5) Trace la droite qui passe par

$O$ et

$G.$

Vérifie qu'elle passe par

$H.$

Exercice 11

Construis le triangle

$ABC$ tel que :

$AB=3.5\;cm\;,\ \widehat{ABC}=120^{\circ}\text{ et }BC=5\;cm.$

1) Trace en bleu la hauteur issue de

$A$ et en vert la médiatrice du segment

$[BC].$

2) Démontre que ces deux droites sont parallèles.

Exercice 12

$ABC$ est un triangle de centre de gravité

$G.$

$E\;,\ D\text{ et }F$ sont les milieux respectifs de

$[AC]\;,\ [AB]\text{ et }[BC].$

On donne :

$AE=2\;cm\;,\ AG=3\;cm\;,\ GD=1\;cm\text{ et }BE=6\;cm.$

Calcule

$AC\;,\ GF\;,\ GC\;,\ BG\text{ et }GE.$

Justifie.

Exercice 13

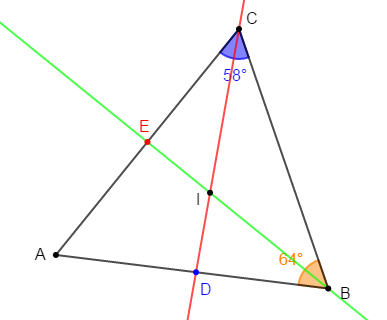
Sur la figure ci-dessous,

$\widehat{ABC}=64^{\circ}\text{ et }\widehat{ACB}=58^{\circ}.$

$(BE)$ est la bissectrice de l'angle

$\widehat{B}$ et

$(CD)$ est la bissectrice de l'angle

$\widehat{C}.$

Les deux bissectrices se coupent en

$I.$

Calcule la mesure des angles

$\widehat{ACD}$ ,

$\widehat{ADC}$ ,

$\widehat{BIC}$ ,

$\widehat{BAC}.$

Justifie.

Exercice 14

On donne un segment

$[AK].$

Soit

$J$ son milieu.

Place un point

$L$ n'appartenant pas à

$(AK)$ tel que

$JL=6\;cm.$

Place sur

$[JL]$ le point

$G$ tel que

$LG=4\;cm.$

$(KG)$ coupe

$(AL)$ en

$I.$

Démontre que

$I$ est le milieu de

$[AL].$

Exercice 15

$MNP$ est un triangle isocèle en

$M$ ,

$K$ est le milieu de

$[NP].$

Les bissectrices

$(PZ)$ et

$(NT)$ des angles

$\widehat{MPN}$ et

$\widehat{MNP}$ se coupent en

$I.$

Démontre que

$(MK)$ passe par

$I.$

Exercice 16

$KELI$ est un parallélogramme de centre

$O.$

1) Construis le point

$M$ centre de gravité du triangle

$KEI$ et le point

$N$ centre de gravité du triangle

$ILE.$

2) Démontre que les points

$K\;,\ M\;,\ O\;,\ N\$ et

$\ L$ sont alignés.

3) Démontre que

$KM=MN=NL.$

Exercice 17

1) Construis un segment

$[UV]$ et sa médiatrice

$(\Delta).$

Marque un point

$K$ sur cette médiatrice,

$K$ n'appartient pas à

$[UV]$ et le point

$M$ symétrique de

$U$ par rapport à

$K.$

2) Démontre que

$K$ est le centre du cercle circonscrit au triangle

$MUV.$

3) La parallèle à

$(UV)$ passant par

$K$ coupe

$(MV)$ en

$J.$

Démontre que

$(KJ)$ est la médiatrice du segment

$[MV].$

Exercice 18

Trace un triangle

$ABC.$

On appelle

$D$ le symétrique de

$A$ par rapport à

$B$ et

$E$ le symétrique de

$A$ par rapport à

$C.$

1) Démontre que les droites

$(BC)$ et

$(DE)$ sont parallèles.

2) On appelle

$I$ le milieu du segment

$[BC].$

La droite

$(AI)$ coupe

$(DE)$ en

$H.$

Démontre que

$I$ est le milieu du segment

$[AH].$

3) Démontre que les droites

$(DC)$ ,

$(AH)$ et

$(BE)$ sont concourantes.

Exercice 19

Soit un parallélogramme

$ABCD.$

Le point

$E$ est le symétrique de

$D$ par rapport à

$C.$

Les droites

$(AD)$ et

$(BE)$ se coupent en

$F.$

1) Montre que

$B$ est le milieu de

$[EF].$

2) Montre que

$A$ est le milieu de

$[DF].$

3) Les droites

$(DB)$ et

$(FC)$ se coupent en

$G.$

Démontre que les points

$E$ ,

$G$ et

$A$ sont alignés.

Exercice 20

1) Construis un triangle

$EFG$ rectangle en

$F.$

Place

$K$ le milieu du segment

$[EG].$

Trace la droite passant par

$K$ et perpendiculaire à

$(EF).$

Elle coupe

$[EF]$ en

$L.$

2) Démontre que

$L$ est le milieu du segment

$[EF].$

3) Les droites

$(FK)$ et

$(GL)$ se coupent en

$M.$

Que représentent les droites

$(FK)$ et

$(GL)$ pour le triangle

$EFG$ ?

Déduis-en que la droite

$(EM)$ coupe le segment

$[FG]$ en son milieu.

Exercice 21

$MIL$ est un triangle,

$A$ ,

$B$ et

$C$ les milieux respectifs des cotés

$[MI]$ ,

$[IL]$ et

$[ML].$

Soit

$G$ son centre de gravité.

1) Démontre que le quadrilatère

$MABC$ est un parallélogramme.

$(AC)$ et

$(MB)$ se coupent en

$J.$

Démontre que

$J$ est le milieu de

$[AC].$

3) Démontrer que

$G$ est le centre de gravité du triangle

$ABC.$

Exercice 22

$PQR$ est un triangle.

1) Construis le point

$M$ milieu de

$[PQ]$ et le point

$K$ , symétrique de

$P$ par rapport à

$R.$

La droite

$(KM)$ coupe le segment

$[RQ]$ en

$I$ et la droite

$(PI)$ coupe

$[KQ]$ en

$N.$

2) Démontre que

$N$ est le milieu du segment

$[KQ].$

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

Auteur:

Diny Faye & adem

Commentaires

Anonyme (non vérifié)

sam, 10/19/2019 - 15:56

Permalien

Bonjour j'ai besoin de la

Bonjour j'ai besoin de la série et correction si possible: sldlldiallo91@gmail.com

répondre

Anonyme (non vérifié)

dim, 04/12/2020 - 14:57

Permalien

Et moi j'ai besoin de la

Et moi j'ai besoin de la correction

répondre

OUSMANE DIOUF (non vérifié)

mer, 07/01/2020 - 14:31

Permalien

Bonjour j'ai besoin de la

Bonjour j'ai besoin de la correction de cette série

répondre

Bineta (non vérifié)

mer, 04/14/2021 - 07:44

Permalien

Correction svp

Correction

répondre

Anonyme (non vérifié)

ven, 05/21/2021 - 13:11

Permalien

On a besoin la correction des

On a besoin la correction des exercices concernant les droites remarquables. svp

répondre

merci (non vérifié)

jeu, 03/23/2023 - 23:37

Permalien

merci pour tout se que vous

merci pour tout se que vous faite

répondre

Miss talia (non vérifié)

mer, 03/06/2024 - 19:10

Permalien

Bitch

répondre

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.

Vous êtes ici

Série d'exercices : Droites remarquables 4e

Formulaire de recherche

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Exercice 5

Exercice 6

Exercice 7

Exercice 8

Exercice 9

Exercice 10

Exercice 11

Exercice 12

Exercice 13

Exercice 14

Exercice 15

Exercice 16

Exercice 17

Exercice 18

Exercice 19

Exercice 20

Exercice 21

Exercice 22

Commentaires

Ajouter un commentaire

Plain text