Fonction logarithme népérien - TL

I. Étude de la fonction logarithme népérien

1. Définition et notation

La fonction logarithme népérien notée $\ln$ est la fonction  définie et dérivable $]0\ ;\ +\infty[$ qui s'annule en $1$ et qui a pour fonction dérivée la fonction définie par $\dfrac{1}{x}.$

Autrement dit :

$\bullet\ $L'ensemble de définition de la fonction $\ln$ est $]0\ ;\ +\infty$ et pour tout $x\in]0\ ;\ +\infty[$,
 
l'image de $x$ par la fonction logarithme népérien est le réel noté $\ln x$

$\bullet\ \ln 1=0$

$\bullet\ $La fonction $\ln$ est dérivable sur $]0\ ;\ +\infty[$ et pour tout $x>0$, on a  $\left(\ln\right)^{'}(x)=\dfrac{1}{x}$

2. Propriétés :  

Si $a> 0$ et $b>0$ alors on a :

$\bullet\ \ln(a\times b)=\ln a+\ln b$ (propriété fondamentale )

$\bullet \ \ln\left(\dfrac{1}{a}\right)=-\ln a$

$\bullet\ \ln\left(\dfrac{a}{b}\right)=\ln a-\ln b$

$\bullet\ $Pour tout nombre rationnel $r$, $\ln  a^{r}=r\ln a$

$\bullet\ \ln\sqrt{a}=\dfrac{1}{2}\ln a$

Remarque

$\bullet\ \dfrac{\ln a}{\ln b}\neq a-\ln b$

$\bullet\ \left(\ln a\right)^{r}\neq r\ln a$

Exemple : Exprimons à l'aide de $\ln 2$ et $\ln 3$, le nombre suivant :

$\ln (2\times 3) +\ln\dfrac{1}{3}-\ln 2^{3}+\ln \dfrac{3}{2}$

3. Représentation graphique de $\ln$

Soit $f$ la fonction définie par $f(x)=\ln x$

$\bullet\ D_{f}=]0\ ;\ +\infty[$

$\bullet\ $limites aux bornes de $D_{f}$ :

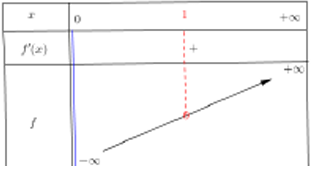
$\bullet\ \lim\limits_{x\longrightarrow 0^{+}}f(x)=\lim\limits_{x\longrightarrow 0^{+}}\ln x=-\infty$

$\bullet\ \lim\limits_{x\longrightarrow\,+\infty}f(x)=\lim\limits_{x\longrightarrow\,+\infty}\ln x=+\infty$

$\bullet\ $Branches infinies

$\bullet\ \lim\limits_{x\longrightarrow\longrightarrow +\infty}f(x)=-\infty$ donc la droite d'équation $x=0$ est une asymptote verticale de $C_{f}$

$\bullet\ \lim\limits_{x\longrightarrow\,+\infty}\dfrac{f(x)}{x}=\lim\limits_{x\longrightarrow\,+\infty}=0$ donc l'axe des abscisses est une branche parabolique de $C_{f}$ en $+\infty$

$\bullet\ $Tableau de variation

Pour tout $x\in]0\ ;\ +\infty[$, $f'(x)=(\ln)'(x)=\dfrac{1}{x}$ or $\dfrac{1}{x}>0$ sur $]0\ ;\ +\infty[$ donc $f$ est strictement croissante sur $]0\ ;\ +\infty[$

$\bullet\ $Remarque

Il existe un unique réel noté $\mathrm{e}$ tel que $\mathrm{e}\in]0\ ;\ +\infty[$ ; $\ln\mathrm{e}=1$ et qu'une valeur approchée de est $\mathrm{e}\approx 2.718$

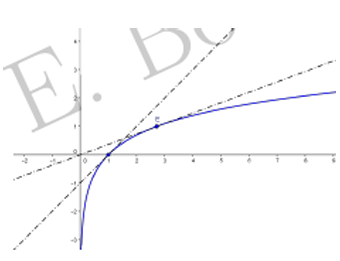
$\bullet\ $courbe représentative de $\ln$

$\bullet\ $Équations des tangentes aux points d'abscisses $1$ et $\mathrm{e}$

L'équation de la tangentes $\left(T'\right)$ à $C_{f}$ au points d(abscisse $1$ est $(T)$ : $y=f'(1)(x-1)+f(1)=x-1$

L'équation de la tangente $\left(T'\right)$ à $C_{f}$ au point d'abscisse $\left(T'\right)$ : $\begin{array}{rcl} y&=&f'(e)(x-e)+f(e)\\&=&\dfrac{1}{\mathrm{e}}(x-e)+1\\&=&\dfrac{1}{e}x \end{array}$

$\bullet\ $Tableau e valeurs $$\begin{array}{|c|c|c|c|c|c|} \hline x&1&e&4&5&6\\ \hline \ln x&0&1&1.4&1.6&1.8\\
\hline \end{array}$$

$\bullet\ $Courbe

Équations et inéquations faisant intervenir $\ln$
 
1. Équations

$\bullet\ $Propriété  

Si $a>0$ et $b<0$ alors on a : $\ln(a)=\ln(b)\Longleftrightarrow\,a=b$

$\bullet\ $Équation du type $\ln(u(x))=\ln(v(x))$

Pour résoudre une telle équation, on procède ainsi :

$\bullet\ $On résout le système d'inéquation $\left\lbrace\begin{array}{rcl} u(x)&>&0\\ v(x)&>&0
\end{array}\right.$

L'ensemble des solutions de ce  système est appelé domaine de validité de l'équation et est noté $D_{v}$
 
$\bullet\ $Dans $D_{v}$, l'équation $\ln(u(x))=\ln(v(x))$ devient $u(x)=v(x).$

Ainsi on résout dans $D_{v}$, l'équation $u(x)=v(x)$
 
$\bullet\ $Exemple : Résolvons dans $\mathbb{R}$ l'équation $\ln(-x+1)=\ln(2x+6)$

2. Inéquations
 
$\bullet\ $Propriété

Si $a> 0$ et $b> 0$ alors on a :

$\bullet\ \ln(a)\leq \ln(b)\Longleftrightarrow,a\leq b$

$\bullet\ \ln(a)\geq \ln(b)\Longleftrightarrow\, a\geq b$

NB : Dans chacun des cas ci-dessus, les inégalités larges peuvent être remplacées par des inégalités strictes.

$\bullet\ $Inéquation du type $\ln(u(x))\leq \ln(v(x))$

Pour résoudre une telle inéquation, on procède ainsi :

$\bullet\ $On détermine $D_{v}$ en résolvant le système $\left\lbrace\begin{array}{rcl} u(x)&>& 0\\
v(x)> 0 \end{array}\right.$

$\bullet\ $Dans $D_{v}$, l'inéquation $\ln(u(x))\leq (v(x))$ devient $u(x)\leq v(x)$

Ainsi on résout  l'inéquation $u(x)\leq v(x)$ dont l'ensemble des solutions sera notée $S_{1}$

L'ensemble des solutions $S$ de l'inéquation est donnée par $S=S_{1}\cap D_{v}$

$\bullet\ $Exemple : Résolvons dans $\mathbb{R}$ l'inéquation $\ln(2x-1)\leq \ln(x+1)$

$\bullet\ $Nb : Pour résoudre une inéquation du type $\ln(u(x))\geq \ln(v(x))$, on procède de la
même manière mais en remplaçant $\leq$ par $\geq$

 
1. Limites usuelles

$\bullet\ \lim\limits_{x\longrightarrow 0^{+}}x\ln x=0$
 
$\bullet\ $Si $n$ est un entier naturel non nul alors $\lim\limits_{x\longrightarrow 0^{+}}x^{n}\ln x=0$

2. Ensemble de définition
 
Soit $u$ une fonction et $f$ la fonction définie par $f(x)=\ln[u(x)]$

$f(x)$ existe ssi $u(x)$ existe et $u(x)> 0$

$\bullet\ $Exemple

Déterminons l'ensemble définition de la fonction  $f$ elle que $f(x)=\ln\left(\dfrac{x+1}{x-1}\right)$

3. Limites de $\ln[u(x)]$
 
Pour calculer $\lim\limits_{x\longrightarrow\, a}\ln[u(x)]$, on calcule d'abord $\lim\limits_{x\longrightarrow a}u(x)$

$\bullet\ $Si $\lim\limits_{x\longrightarrow\, a}u(x)=b$ avec $b> 0$ alors $\lim\limits_{x\longrightarrow\, a}\ln[u(x)]=\ln b$

$\bullet\ $Si $\lim\limits_{x\longrightarrow\,a}u(x)=0$ alors $\lim\limits_{x\longrightarrow\,a}\ln[u(x)]=-\infty$

$\bullet\ $Si $\lim\limits_{x\longrightarrow\,a}u(x)=+\infty$ alors $\lim\limits_{x\longrightarrow a}\ln[u(x)]=+\infty$

$\bullet\ $Exemple : calculons les limites suivantes

$\bullet\ \lim\limits_{x\longrightarrow\,+\infty}\ln\left(\dfrac{2x+1}{x-1}\right)$

$\bullet\ \lim\limits_{x\longrightarrow\,+\infty}\ln\left(\dfrac{x+1}{x^{2}+1}\right)$

$\bullet\ \lim\limits_{x\longrightarrow\, 0}\ln\left(\dfrac{1}{x^{2}}\right)$

4. Dérivée

Si $\begin{array}{rcl} f(x)&=&\ln[u(x)]\\&\text{alors }f'(x)\\&=&\ln'[u(x)]\\&=&\dfrac{u'(x)}{u(x)}
\end{array}$

$\bullet\ $Exemple

$f(x)=\ln\left(x^{x}+x-6\right)$.

Calculons $f'(x)$