Vous êtes ici

Exercices : Racine carrée 3e

Classe:

Troisième

Exercice 1

Donner une écriture simple des nombres réels suivants :

$A=\sqrt{200}-3\sqrt{18}+6\sqrt{2}+50$

$B=(\sqrt{2}+2)^{2}$

$C=(3\sqrt{2}-5)^{2}$

$D=(3\sqrt{2}+5)(3\sqrt{2}-5)$

$E=\sqrt{19-\sqrt{1+\sqrt{8^{2}}}}$

Exercice 2 "au BFEM du 2e groupe"

Répondre par vrai on faux en justifiant la réponse :

1) $\sqrt{40}=20\;,\quad$ 2) $7\sqrt{2}=\sqrt{98}\;,\quad$ 3) $\sqrt{64+25}=8+5=13$

Exercice 3

On considère les nombres réels définis par :

$X=\dfrac{\sqrt{5}}{\sqrt{5}-\sqrt{3}}-\dfrac{\sqrt{3}}{\sqrt{5}+\sqrt{3}}$ et $Y=(3\sqrt{2}-\sqrt{3})^{2}+6\sqrt{6}$

Montrer que $X$ et $Y$ sont des nombres entiers naturels.

Exercice 4

On donne les nombres réels suivants tels que :

$X=\sqrt{4+\sqrt{7}}-\sqrt{4-\sqrt{7}}$ et $Y=\sqrt{3-2\sqrt{2}}-\sqrt{3+2\sqrt{2}}$

1) Déterminer les signes respectifs de $X$ et $Y.$

2) Calculer $X^{2}$ et $Y^{2}.$

3) En déduire $X$ et $Y.$

Exercice 5

L'unité de longueur est le $hm.$ Les dimensions d'un champ rectangulaire sont : $2\sqrt{3}+2$ et $2\sqrt{3}-2.$

Calculer : Le périmètre, l'aire ensuite le diamètre du cercle circonscrit de ce champ rectangulaire.

Exercice 6 "BFEM 2009"

On donne les réels : $a=2-\dfrac{3\sqrt{2}}{2}$ et $b=\dfrac{1}{3\sqrt{2}+4}$

1) Rendre rationnel le dénominateur de $b$ puis montrer que les nombres $a$ et $b$ sont des opposés.

2) Soit $A=\sqrt{(1-2\sqrt{2})^{2}}+(\sqrt{2}-2)^{2}-\sqrt{18}.$

Montrer que $A=5-5\sqrt{2}$ puis encadre-le à $10^{-2}$ prés sachant que :

$1.414<\sqrt{2}<1.415.$

Exercice 7

1) Calculer la valeur numérique de l'expression suivante : $$C=\dfrac{2x}{2-x}-\dfrac{2-x}{x}\quad\text{ pour }x=2-\sqrt{3}$$

2) Écrire les expressions suivantes sous la forme $$a\sqrt{b}\quad\text{ avec }a\in\mathbb{Q}\text{ et }b\in\mathbb{N}$$

$A=\sqrt{363}+5\sqrt{3}+\sqrt{2}\times\sqrt{54}-3\sqrt{12}$

$B=\sqrt{20}-\dfrac{2}{3}\sqrt{80}+7\sqrt{2.45}$

$C=2\sqrt{75}-4\sqrt{48}+7\sqrt{192}$

$D=-15\sqrt{96}+18\sqrt{54}+3\sqrt{486}-21\sqrt{24}$

$E=\sqrt{2}\sqrt{3}-\sqrt{54}+\sqrt{\dfrac{24}{49}}$

$F=\dfrac{7}{3}\sqrt{\dfrac{54}{16}}-\dfrac{6}{5}\sqrt{\dfrac{30}{20}}-\dfrac{9}{2}\sqrt{\dfrac{24}{81}}$

Exercice 8

1) Rendre rationnel le dénominateur des nombres suivants :

$\dfrac{5-2\sqrt{3}}{3\sqrt{3}-5}\;,\quad\dfrac{3\sqrt{5}-3}{2\sqrt{3}}\;,\quad\dfrac{2}{3\sqrt{2}-2\sqrt{3}}$

2) Mettre les expressions suivantes sous la forme $$a+b\sqrt{c}\quad\text{ avec }a\in\mathbb{Q}\;,\ b\in\mathbb{Q}\text{ et }c\in\mathbb{N}$$

$A=\dfrac{2}{1-\sqrt{3}}+\dfrac{1}{1+\sqrt{3}}\;,\quad B=\dfrac{\sqrt{3}}{\sqrt{3}-\sqrt{2}}+\dfrac{\sqrt{2}}{\sqrt{3}+\sqrt{2}}$

3) Donner une écriture simplifiée de :

$C=3\sqrt{\dfrac{1}{75}}\times 2\sqrt{\dfrac{3}{4}}\;,\quad D=\sqrt{\left(\dfrac{3}{2}\right)^{2}}+4$

$E=(1-\sqrt{2})(5\sqrt{2}+3)+(1-\sqrt{2})^{2}\;,\quad F=\sqrt{\dfrac{1.6\times 2.5}{0.36}}$

4) Écris sans le grand radical.

$F=\sqrt{(1-\sqrt{5})^{2}}\;,\quad G=\sqrt{(-5-\sqrt{3})^{2}}$

$H=\sqrt{(5-2\sqrt{3})^{2}}\;,\quad I=\sqrt{(-2\sqrt{3}+4)^{2}}$

$J=\sqrt{\left(\dfrac{3}{2}-2\sqrt{2}\right)^{2}}$

Exercice 9

1) Écrire $A=\sqrt{121}-2\sqrt{112}+\sqrt{63}-\sqrt{81}$ sous la forme $$p+q\sqrt{c}\quad(p\in\mathbb{Z}\;,\ q\in\mathbb{Z}\;,\ c\in\mathbb{N})$$

2) Soit l'expression $B(x)=x^{2}-1+(x+7)(2-2x).$

a) Développer, réduire puis ordonner $B(x).$

b) Factoriser $B(x).$

3) Soit l'expression $q(x)=\dfrac{B(x)}{(x-1)(x+7)}$

a) Établir la condition d'existence de $q(x)$ et la Simplifier.

b) Calculer $q(\sqrt{2})$ (sans radicale au dénominateur).

c) Donner un encadrement de $q(\sqrt{2})$ d'amplitude 0.1 prés sachant que

$1.41<\sqrt{2}<1.42.$

Exercice 10

On donne $A=\dfrac{\dfrac{4}{-\sqrt{5}-2}}{\dfrac{1}{2-\sqrt{5}}}$ et $B=4-2\sqrt{5}$

1) Écrire $A$ et $B^{2}$ sous la forme $x+y\sqrt{5}$. En déduire une écriture simplifiée de $C=\sqrt{A}.$

2) Sachant que $2.23<\sqrt{5}<2.24$ ; donner un encadrement de $B$ et $C$ à $10^{-1}$ près.

Exercice 11

On donne $a=\dfrac{-6}{2\sqrt{3}-3\sqrt{2}}$ et $b=4-2\sqrt{3}$

1) Écrire $a$ sous la forme $x\sqrt{3}+y\sqrt{2}$ puis calculer $a^{2}.$

En déduire une écriture simplifiée de $C=\dfrac{30+12\sqrt{6}}{2\sqrt{3}-3\sqrt{2}}.$

2) Calculer $b^{2}$ puis montrer que $d=\dfrac{12-3\sqrt{12}}{\sqrt{28-16\sqrt{3}}}\in\mathbb{N}$

Exercice 12

1) Écrire sous la forme $a\sqrt{b}$ où $a$ et $b$ sont des entiers : $\sqrt{45}\;;\ \sqrt{12}\;;\ \sqrt{20}.$

2) Écrire $C=\sqrt{45}+\sqrt{12}+\sqrt{20}-2\sqrt{3}$ sous la forme $d\sqrt{5}$ où $d$ est un entier.

3) Montrer que $E=(1+\sqrt{2})^{2}-(\sqrt{8}-1)$ est un entier.

Exercice 13

On donne $a=\sqrt{10}-3$ et $b=\sqrt{\dfrac{\sqrt{10}-3}{\sqrt{10}+3}}$

1) Calculer $a^{2}$ puis rendre rationnel le dénominateur de $\dfrac{\sqrt{10}-3}{\sqrt{10}+3}$

2) Simplifier l'écriture de $b$.

3) Sachant que $3.162<\sqrt{10}<3.163$ ; donner un encadrement de $3-\sqrt{10}$ au dixième près.

Exercice 14

Soient les réels $x$ et $y$ tels que $$x=\dfrac{2+\sqrt{3}}{2-\sqrt{3}}+\dfrac{2-\sqrt{3}}{2+\sqrt{3}}\;;\quad y=\sqrt{50}-\sqrt{32}-\sqrt{18}$$

1) Montrer que $x$ est un entier que l'on précisera.

2) Écrire $y$ sous la forme $a\sqrt{b}$ avec $b$ un entier naturel.

3) Donner un encadrement de $x-y$ à $10^{-2}$ près.

Exercice 15

1) Simplifier les réels suivants :

$A=-\sqrt{49}3+\sqrt{12}-\sqrt{(-5)^{2}}$

$B=\sqrt{12}+\sqrt{32}-\sqrt{144}-\sqrt{2}$

$C=3\sqrt{a^{4}}+a\sqrt{a^{2}}-5a^{2}$ avec $a\in\mathbb{R}^{-}$

2) Comparer les réels

$-2\sqrt{5}\quad$ et $\quad-3\sqrt{5}$

$3-2\sqrt{2}\quad$ et $\quad-1+\sqrt{2}$

$\sqrt{5-2\sqrt{3}}\quad$ et $\quad\sqrt{3-\sqrt{3}}$

Exercice 16

1) On donne $a=2+\sqrt{5}$ et $b=2-\sqrt{5}$. Calculer $a^{2}$ et $b^{2}$ puis en déduire une écriture simplifiée de $A=\sqrt{9+4\sqrt{5}}+\sqrt{9-4\sqrt{5}}.$

2) On donne

$X=\sqrt{3+2\sqrt{2}}$ et $Y=\sqrt{3-2\sqrt{2}}$

a) Calculer $X.Y$ ; que peut-on dire de $X$ et $Y$ ?

b) On pose $M=X-Y$ ; calculer $M^{2}$ puis en déduire que $M=2.$

Exercice 17

1) On donne $C=\sqrt{5\sqrt{2}-7}$ et $D=\sqrt{5\sqrt{2}+7}.$

Montre que $C$ et $D$ sont inverses.

2) $E=\dfrac{3\sqrt{2}-1}{\sqrt{2}}$.

Après avoir rendu rationnel le dénominateur de $E$, encadrer $E$ à $10^{-2}$ près sachant que $1.414<\sqrt{2}<1.415.$

3) $F=\sqrt{2}\sqrt{48}-3\sqrt{54}+5\sqrt{6}$. Montrer que $F=0$

Exercice 18

1) On pose $a=1+\sqrt{5}$ et $b=1-\sqrt{3}$ ; calculer $a^{2}$ et $b^{2}.$

2) Simplifier $c=\dfrac{1+\sqrt{5}}{6+2\sqrt{5}}$ puis rendre rationnel son dénominateur.

3) Calculer $a.c$. Que représente $a$ pour $c$ ?

4) On donne $A=\sqrt{(6-2\sqrt{5})^{2}-2(6-2\sqrt{5})(3+3\sqrt{5})+(3+3\sqrt{5})^{2}}$

a) Simplifier $A$.

b) Donner la valeur approchée de $A$ à $10^{-2}$ près par défaut sachant que

$2.236<\sqrt{5}< 2.237.$

Exercice 19

On donne $a=1-\sqrt{3}$ et $b=6\sqrt{1-\dfrac{\sqrt{3}}{2}}$.

1) Calculer $a^{2}$ et $b^{2}$. Montrer que $b=-3a.$

2) On donne $E=\dfrac{2-\sqrt{12}}{6\sqrt{1-\dfrac{\sqrt{3}}{2}}}$ ; montrer que $E$ est un rationnel.

Exercice 20 "BFEM 2008"

On donne $a=\sqrt{7+4\sqrt{3}}\ $ et $\ b=\sqrt{7-4\sqrt{3}}$

1) Calculer $a^{2}\;;\ b^{2}\;;\ a\times b\;;\ (a+b)^{2}\ $ et $\ (a-b)^{2}$

2) En déduire $a+b\ $ et $\ a-b$

Exercice 21

Soit $A=\sqrt{2}-3\ $ et $\ B=\dfrac{5\sqrt{2}-1}{\sqrt{2}+1}$

1) Calculer $A^{2}$ puis rendre rationnel le dénominateur de $B.$

2) En déduire une écriture simplifiée de $\sqrt{B}.$

Résoudre dans $\mathbb{R}$, l'équation : $(\sqrt{2}+1)x^{2}-5\sqrt{2}+1=0$

Exercice 22

1) Comparer en justifiant :

$\dfrac{-2\sqrt{3}}{3}\quad $ et $\quad \dfrac{\sqrt{2}}{7}$

$\sqrt{7}+4\quad $ et $\quad \sqrt{7}-1$

$2\sqrt{2}-1\quad $ et $\quad 3-\sqrt{2}$

$\sqrt{9+4\sqrt{5}}\quad $ et $\quad \sqrt{9-4\sqrt{5}}$

2) Écrire plus simplement :

$\sqrt{2^{2}\times 4^{2}\times 3^{2}\times 5^{2}}\;,\quad\sqrt{7^{2}\times 2^{2}\times 5^{3}\times 3^{8}}$

$\sqrt{36^{2}\times b^{5}\times c^{4}\times a^{-2}}\quad$ avec $a>0$ et $b\geq 0$

$\sqrt{4+\sqrt{29-\sqrt{14+\sqrt{3+\sqrt{1}}}}}$

$\dfrac{1}{4}\sqrt{13+\sqrt{\dfrac{15}{2}+3\sqrt{\dfrac{1}{4}}}}$

Exercice 23

On donne : $P=2-\dfrac{3\sqrt{2}}{2}\ $ et $\ Q=\dfrac{1}{3\sqrt{2}+4}$

1) Montrer que $P$ et $Q$ sont des opposés.

2) Sachant que $1.414<\sqrt{2}<1.415$. Encadrer à $10^{-2}$ près $P$ et $Q$.

3) On donne $3.316<\sqrt{11}<3.317$ encadrer à $10^{-1}$ près $\dfrac{a}{b}$ sachant que $a=2\sqrt{11}-6$ et $b=2\sqrt{11}+6$

Exercice 24

On donne $a=\sqrt{28+16\sqrt{3}}\ $ et $\ b=\sqrt{28-16\sqrt{3}}$

1) Montrer que $a\times b=4$

2) On pose $u= a+b\ $ et $\ v=a-b$. Calculer $u^{2}$ et $v^{2}$ puis en déduire $u$ et $v.$

3) On donne $X=\dfrac{u+v}{2}\ $ et $\ Y=\dfrac{u-v}{2}$. Trouver $X$ et $Y$ puis montrer que $a=X$ et $b=Y.$

4) Donner la valeur approchée par défaut de $b$ à $10^{-2}$ près sachant que $1.732<\sqrt{3}<1.733.$

Exercice 25

Soient $a\;,\ b\;,\ c$ trois réels tels que :

$a(\sqrt{3}+1)=\sqrt{3}-1\;,\ b=\sqrt{2-\sqrt{3}}$ et $c=\left(\dfrac{\sqrt{6}-\sqrt{2}}{2}\right)^{2}$

1) Calculer $a$ et rendre rationnel son dénominateur.

2) Écrire $c$ sous la forme $x+y\sqrt{3}.$

3) a) Montrer que $a=c$ puis en déduire une écriture simplifiée de $b.$

b) Encadrer $b$ à $10^{-1}$ près sachant que

$1.414<\sqrt{2}<1.415$ et $2.449<\sqrt{6}<2.450$

Exercice 26

1) Déterminer le réel $a$ tel que $36a=1296$ puis en déduire $\sqrt{1296}.$

2) On donne $x=3+2\sqrt{2}\;;\ y=3-2\sqrt{2}$ et $z=\dfrac{\sqrt{5}+1}{2}$

a) Calculer $x^{2}\;,\ y^{2}\;,\ xy$ et $\dfrac{x}{y}$

b) Montrer que $\dfrac{x}{y}+\dfrac{y}{x}$ est un entier relatif.

c) Montrer que $\dfrac{1}{z}=z-1$

Exercice 27

1) On donne $P=\left(\dfrac{\sqrt{2}-\sqrt{3}}{\sqrt{2}}:\dfrac{1}{\sqrt{2}+\sqrt{3}}\right)\times \dfrac{\sqrt{2}}{4\sqrt{3}}$.

Montrer que $P=-\dfrac{\sqrt{3}}{12}$.

2) On donne $Q=-2\sqrt{48}+3\sqrt{192}-4\sqrt{75}$

a) Écrire $Q$ sous la forme $a\sqrt{b}\ $ ($a\in\mathbb{Z}\;;\ b\in\mathbb{N}$)

b) Encadrer $Q$ par deux entiers consécutifs.

3) Montrer que $P$ et $Q$ sont des inverses.

4) En déduire que $P(P-1)=\dfrac{P-1}{Q}$.

Exercice 28

1) On considère l'expression $X=\sqrt{300}+2\sqrt{3}-4\sqrt{75}.$

Écris $X$ sous la forme $a\sqrt{b}$ ; où $a$ et $b$ sont des entiers relatifs.

2) Calcule $\left(2-\sqrt{3}\right)^{2}$ puis déduis-en l'écriture de $Y=\sqrt{7-4\sqrt{3}}.$ avec un seul radical.

Exercice 29

Écris le plus simplement possible les expressions suivantes :

$A=5\sqrt{300}+\sqrt{27}-3\sqrt{147}$ et

$B=\dfrac{\sqrt{6-\sqrt{11}}\times\sqrt{6+\sqrt{11}}}{5}.$

Exercice 30

1) Calcule $\left(1+\sqrt{5}\right)^{2}$ et $\left(1-\sqrt{5}\right)^{2}$

2) On donne $X=\sqrt{6-2\sqrt{5}}$ et $Y=\sqrt{6+2\sqrt{5}}$

a) Écris $X$ et $Y$ avec un seul radical.

b) Calcule $X+Y$ et $X-Y.$

Exercice 31

On donne $a=5-2\sqrt{6}$ et $b=5+2\sqrt{6}.$

1) Calcule $a\times b.$

Que peux-tu en déduire ?

2) Calcule $a^{2}\;;\ b^{2}\text{ et }\dfrac{a}{b}.$

3) Vérifie que $\dfrac{a}{b}+\dfrac{b}{a}$ est un entier naturel.

4) Soit $X=\sqrt{49-20\sqrt{6}}$ et $Y=\sqrt{49+20\sqrt{6}}$

Écris $X$ et $Y$ avec un seul radical.

Exercice 32

On considère l'expression ci-dessous :

$H(x)=4\left( x+\sqrt{3}\right)^{2}-4\sqrt{3}\left(x+\sqrt{3}\right)+3$

1) Développe, réduis et ordonne $H(x).$

2) Déduis-en une factorisation de $H(x).$

Exercice 33

On donne :

$a=\dfrac{2-\sqrt{3}}{5+\sqrt{3}}$

$b=3\sqrt{18}+\sqrt{128}-\sqrt{338}$

$c=\sqrt{2}-3.$

1) Rends rationnel le dénominateur de $a.$

2) Simplifie $b.$

3) Calcule $c^{2}.$

Déduis-en que $p=\dfrac{\sqrt{5}-\sqrt{8}}{3\sqrt{5}-6\sqrt{2}}$ est un rationnel que l'on déterminera.

Exercice 34

Écris le plus simplement possible les expressions ci-dessous :

$$G=\sqrt{76-2\sqrt{37-\sqrt{\dfrac{21}{25}+\dfrac{1}{25}\times\sqrt{6+\sqrt{103-2\sqrt{\dfrac{9}{4}}}}}}}$$

On donne un triangle $ABC$ rectangle en $A$ tel que $AC=\sqrt{3}-1\ $ et $\ BC=2\sqrt{2}.$

1) Calcule $AB^{2}$, déduis-en que $AB=\sqrt{3}+1$ puis l'aire du triangle $ABC.$

2) Calcule $\dfrac{1}{AC}$ sans radical au dénominateur et déduis-en un encadrement de $\dfrac{1}{AC}$ d'amplitude $0.01$

sachant que $1.73<\sqrt{3}<1.74.$

Exercice 35

$ABCD$ et $CHIJ$ sont des carrés de côtés respectifs :

$5\sqrt{3}-1$ et $\sqrt{27}.$ (Voir figure ci-dessous)

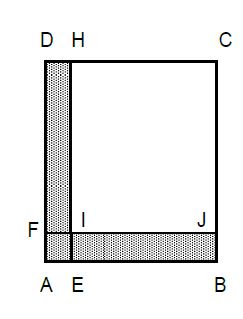
Calcule :

1) l'aire du carré $ABCD$ ;

2) l'aire du carré $CHIJ$ ;

3) la longueur $AE$ ;

4) le périmètre du rectangle $CDFJ$ ;

5) l'aire de la surface coloriée.

Exercice 36

1) Écris les expressions $x$ et $y$ ci-dessous sous la forme $a\sqrt{b}$ où $a$ et $b$ sont des entiers positifs.

a) $x=2\sqrt{50}-3\sqrt{18}+\sqrt{200}-\sqrt{2}.$

b) $y=\sqrt{20}+\sqrt{80}-\dfrac{\sqrt{32}}{\sqrt{12}}\times\sqrt{48}.$

2) On donne les réels $m=1-2\sqrt{3}$ et $n=1+\sqrt{12}$

a) Sans calculer $m^{2}$ et $n^{2}$ montre que $m+n$ , $m\times n$ sont des entiers relatifs.

b) Déduis-en que $m^{2}+n^{2}$ est un entier relatif.

3) On pose $p=\dfrac{m}{n}.$

Rends rationnel le dénominateur de $p.$

Exercice 37

On donne :

$A=\left(\sqrt{5}-\sqrt{3}\right)^{2}$ et $B=x^{2}-7x+10.$

1) Calcule $A$ puis déduis-en l'expression simplifiée du nombre :

$C=\dfrac{1}{2}\left(\sqrt{5}-\sqrt{8-2\sqrt{15}}\right).$

2) Calcule $B$ pour $x=\sqrt{2}.$

3) Donne un encadrement du nombre $D=12-7\sqrt{2}$ sachant que :

$1.414<\sqrt{2}<1.415$, puis déduis-en la valeur approchée de $D$ à $10^{-2}$ près par défaut.

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

Lien cours vidéo:

Exercice Video Racine Carréee

Commentaires

Dadal (non vérifié)

mar, 06/25/2019 - 13:22

Permalien

Dont

Merci

répondre

Tidiane (non vérifié)

dim, 10/27/2019 - 13:44

Permalien

Apprendre

Pour reussite

répondre

Samba ndour (non vérifié)

lun, 08/10/2020 - 11:53

Permalien

Pour réussi l'examen du BFM

Pour réussi l'examen du BFM comment ont fait

répondre

Morzo (non vérifié)

mar, 12/22/2020 - 20:25

Permalien

comment faire ?

C'est simple on apprend ses lecons au jour le jour, on suis en classe, on fait des exercices et le BFEM est dans la poche OK ? J'espére avoir répondu a ta question merci et bonne journée .