Exercices : Isométrie et transformation du plan 3e
Classe:
Troisième
Exercice 1
Le plan est muni d'un repère orthonormé $(O\;;\ \overrightarrow{OI}\;,\ \overrightarrow{OJ}).$ On donne les points $A\begin{pmatrix} 1\\ 1\end{pmatrix}\;,\ B\begin{pmatrix} 3\\ 2\end{pmatrix}$ et $C\begin{pmatrix} 2\\ 3\end{pmatrix}$
1) Trouver les coordonnées de $D$ pour que $ABDC$ soit un parallélogramme. On notera $ABDC$ la figure (1).
2) Construire la figure (2) image de la figure (1) par la translation de vecteur $\overrightarrow{BC}.$
3) Construire la figure (3) image de la figure (1) par la rotation de centre $A$ et d'angle $45^{\circ}$ dans le sens des aiguilles d'une montre.
4) Construire la figure (4) image de la figure (1) par la symétrie centrale de centre $O.$
5) Construire la figure (5) image de la figure (1) par la symétrie orthogonale d'axe $(yy')$ centrale de centre $O.$
(Utiliser des couleurs différentes).
Exercice 2
Le plan est muni d'un repère orthonormé $(O\;;\ \overrightarrow{OI}\;,\ \overrightarrow{OJ})$ On donne les points $K\begin{pmatrix} -2\\ 1\end{pmatrix}\;,\ M\begin{pmatrix} 1\\ -3\end{pmatrix}$ et $N\begin{pmatrix} 2\\ -5\end{pmatrix}.$
1) Trouver les coordonnées de $P$ image de $K$ par la translation de vecteur $\overrightarrow{MN}.$
2) Trouver les coordonnées de $F$ symétrique de $K$ par rapport à $O.$ (On demande de faire la figure).
Exercice 3 BFEM 2009
Dans le plan muni d'un repère orthonormal $(O\;,\ I\;,\ J)$, On donne les points : $A(5\;;\ 0)\;;\ B(6\;;\ 2)$ et $C(2\;;\ 4).$
1) Montrer que le triangle $ABC$ est rectangle en $B.$
2) Construis le point $D$ tel que $\overrightarrow{BD}=\overrightarrow{AB}$ puis calculer ces coordonnées.
3) Construis le point $E$ symétrique de $C$ par rapport à $B$, puis calcule ses coordonnées.
4) Justifier que le quadrilatère $ACDE$ est un losange.
5) Soit $F(12\;;\ 4)$ ; justifier que $F$ est l'image de $E$ par la translation de vecteur.
Exercice 4 Au BFEM du 2nd Groupe.
Répondre par vrai on faux en justifiant la réponse
1) La symétrie de centre $A$ suivie de la symétrie de centre $B$ est égale à la translation de vecteur $2\overrightarrow{BA}.$
2) La translation de vecteur $\vec{u}$ suivie de la translation de vecteur $\vec{v}$ est égale à la somme de $\vec{v}+\vec{u}.$
Exercice 5
Le plan est muni d'un repère orthonormé $(O\;;\ \overrightarrow{OI}\;,\ \overrightarrow{OJ}).$
1) Placer les points $A(1\;;\ -1)\;;\ B(3\;;\ 1)$ et $C(1\;;\ 3).$
2. Montrer que $\overrightarrow{AB}$ et $\overrightarrow{BC}$ sont orthogonaux. En déduire que les droites $(AB)$ et $(BC)$ sont perpendiculaires.
3) Calculer les coordonnées du point $E$ milieu de $[AC].$
4) Construire le point $F$ symétrique de $E$ par le symétrique orthogonal d'axe $(BC)$ suivi de $(AB).$
5) Calculer les coordonnées du point $F.$
Exercice 6 BFEM 2008
Dans le plan muni d'un repère orthonormé $(O\;;\ \overrightarrow{OI}\;,\ \overrightarrow{OJ})$, on donne les droites $(D)$ et $(D')$ telles que :
$(D)\ :\ x-y+1=0$ et $(D')\ :\ x+y+3=0.$
1) Montrer que les droites $(D)$ et $(D')$ sont perpendiculaires.
2) Tracer les droites $(D)$ et $(D')$ dans le repère.
3) Déterminer graphiquement les coordonnées du point d'intersection $A$ de $(D)$ et $(D').$
4) Soit $B(0\;;\ -5).$ Construire le point $E$ image de $B$ par le symétrique orthogonal d'axe $(D')$ suivie de celle d'axe $(D).$ Quelle est la nature de cette transformation du plan ?
5) Trouver les coordonnées de $E.$
Exercice 7
Dans le plan muni d'un repère orthonormé $(O\;;\ \overrightarrow{OI}\;,\ \overrightarrow{OJ})$, on donne les droites $(D_{1})$ et $(D_{2})$ telles que :
$(D_{1})\ :\ y=x$ et $(D_{2})\ :\ y=x+2.$
1) Montrer que les droites $(D_{1})$ et $(D_{2})$ sont parallèles.
2) Tracer les droites $(D_{1})$ et $(D_{2})$ dans le repère.
3) Construire le point $A'$ image $A$ par la symétrique orthogonale d'axe $(D_{1})$ suivi de $(D_{2}).$
4) Déterminer graphiquement les coordonnées du point $A'.$
Exercice 8
Le plan est muni d'un repère orthonormé $(O\;;\ \overrightarrow{OI}\;,\ \overrightarrow{OJ})$
1) Placer les points $N(-1\;;\ -1)\;;\ M(-3\;;\ 1)$ et $C(-1\;;\ 3).$
2) Placer le point $Q$ symétrique de $N$ par rapport à $M$ suivi de $P.$
3) Calculer les coordonnées du point $Q.$
Exercice 9
Trace un triangle équilatéral $ABC$ de $4\;cm$ de côté.
1) Construis l'image du triangle $ABC$ par la symétrie de centre $C$ et hachure au crayon noir l'intérieur de cette image.
2) Construis l'image du triangle $ABC$ par la symétrie orthogonale par rapport à la droite $(BC)$ et hachure au crayon rouge l'intérieur de cette image.
3) Construis l'image du triangle $ABC$ par la rotation de centre $C$, d'angle $120^{\circ}$ et de sens, le sens inverse des aiguilles d'une montre, et hachure au crayon bleu l'intérieur de cette image.
Exercice 10
1) Place trois points $A$, $B$ et $C$ distincts dans le plan.
2) Trace deux droites $(\mathcal{D})$ et $(\mathcal{D'})$ sécantes en $O$ et formant un angle aigu de $45^{\circ}.$
3) Construis le point $B'$ image de $B$ par la symétrie orthogonale par rapport à $(\mathcal{D})$ puis construis le point $B''$ image de $B'$ par la symétrie orthogonale par rapport à $(\mathcal{D'}).$
Par quelle transformation du plan, $B$ a pour image $B''$ ?
Exercice 11
$(\mathcal{D})$ et $(\mathcal{D'})$ sont deux droites parallèles et $ABC$ un triangle dont l'intersection avec chacune des droites $(\mathcal{D})$ et $(\mathcal{D'})$ est vide.
1) Construis les points $A'$, $B'$ et $C'$, images respectives des points $A$, $B$ et $C$ par la symétrie orthogonale par rapport à $(\mathcal{D}).$
2) Construis les points $A''$, $B''$ et $C''$, images respectives des points $A'$, $B'$ et $C'$ par la symétrie orthogonale par rapport à $(\mathcal{D'}).$
3) Quelle est la transformation qui associe $A$ à $A''$ ? $B$ à $B''$ ? $C$ à $C''$ ?
Exercice 12
Construis un triangle $EFG$, rectangle en $F$ tel que $EF=FG=4\;cm.$
(Utilise une feuille de papier quadrillé.)
1) Place le point $K$ image de $E$ par la symétrie de centre $F.$
2) Place le point $L$ image de $F$ par la symétrie orthogonale par rapport à $(EG).$
3) Place le point $J$ image de $G$ par la translation de vecteur $\overrightarrow{EF}.$
4) Place le point $H$ tel que $\overrightarrow{HE}=\overrightarrow{FG}.$
Quelle est l'image de $H$ par la rotation de centre $F$ qui transforme $E$ en $G$ ? Justifie ce résultat.
Exercice 13
Le plan est muni d'un repère orthonormal.
1) Place les points $A(1\;;\ -1)$ ; $B(3\;;\ 1)$ et $C(1\;;\ 3).$
2) Montre que $\overrightarrow{AB}$ et $\overrightarrow{BC}$ sont orthogonaux.
Déduis-en que les droites $(AB)$ et $(BC)$ sont perpendiculaires.
3) Calcule les coordonnées du point $E$ milieu de $[AC].$
4) Construis le point $F$ image de $E$ par la symétrie orthogonale par rapport à $(BC)$ suivi de la symétrie orthogonale par rapport à $(AB).$
5) Calcule les coordonnées du point $F.$
Exercice 14
Dans cet exercice on réalisera le dessin demandé sur une feuille à part.
On commencera le dessin au centre de la feuille.
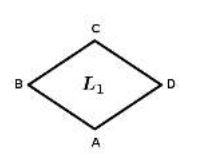
On considère un losange $ABCD$ tel que $AC=6\;cm$ et $BD=4\;cm.$
1) Représente le losange $ABCD$ en vraie grandeur.
On appelle $L_{1}$ ce losange.
2) Construis le symétrique $L_{2}$ du losange $L_{1}$ par rapport à la droite $(AD).$
3) Construis l'image $L_{3}$ du losange $L_{1}$ par la translation de vecteur $\overrightarrow{CB}.$
4) Construis l'image $L_{4}$ du losange $L_{1}$ par la translation de vecteur $\overrightarrow{CB}+\overrightarrow{CD}.$
(Les lettres $L_{2}$, $L_{3}$, $L_{4}$ seront écrites sur la figure.)
Exercice 15
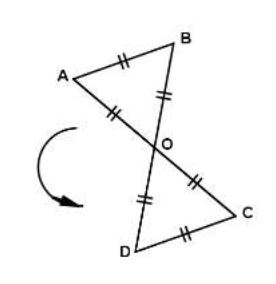
1) Reproduis cette figure en vraie grandeur sachant que $OA=3\;cm$ et que les points $A$, $O$ et $C$, d'une part, et les points $B$, $O$ et $D$, d'autre part, sont alignés.
2) Démontre que $ABCD$ est un rectangle.
3) Place, sur la figure, le point $E$ image du point $O$ par la translation de vecteur $\overrightarrow{BA}.$
4) Place le point $F$ image du point $C$ par la rotation de centre $O$ et d'angle $60^{\circ}$ dans le sens de la flèche.
5) Montre que les points $A$, $B$, $C$, $D$, $E$, $F$ sont sur un même cercle que l'on précisera.
6) Écris un vecteur égal au vecteur $\overrightarrow{CB}+\overrightarrow{CD}.$
Exercice 16
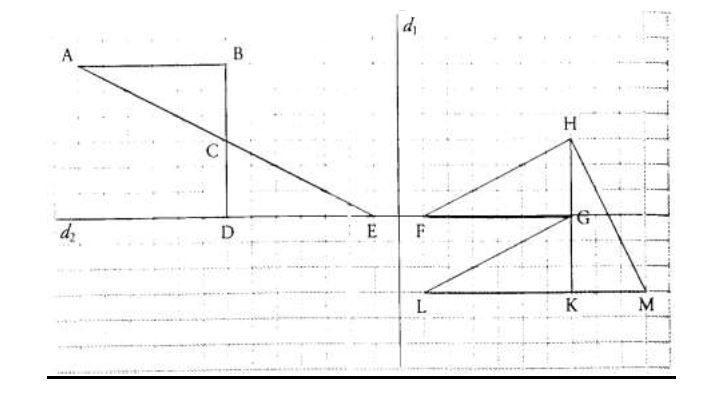
On a représenté sur le quadrillage ci-dessous cinq triangles rectangles de mêmes dimensions.
Sans justification, réponds aux questions ci-dessous :
1) Quelle est l'image du triangle $FGH$ par la symétrie orthogonale par rapport à $d_{1}$ ?
2) Quelle est l'image du triangle $GKL$ par la rotation de centre $K$, d'angle $90^{\circ}$ dans le sens des aiguilles
d'une montre ?
3) Quelle est la transformation par laquelle on passe du triangle $ABC$ au triangle $EDC$ ?
4) Quelle est la transformation par laquelle on passe du triangle $GKL$ au triangle $HGF$ ?
Exercice 17
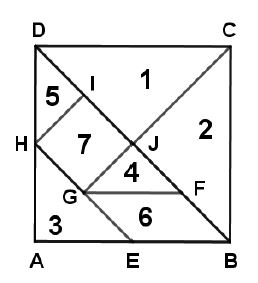
Le puzzle chinois découpé dans un carré est formé de $5$ triangles rectangles isocèles :
$1$, $2$, $3$, $4$, $5$ d'un parallélogramme $6$ et d'un carré $7.$
En observant le dessin de ce puzzle, réponds aux questions ci-dessous :
a) Quelle est l'image de $B$ par la symétrie de centre $F$ ?
b) Quelle est l'image de $A$ par la symétrie orthogonale par rapport à $(BD)$ ?
c) Quelle est l'image de $H$ par la translation de vecteur $\overrightarrow{GF}$ ?
d) Quelle est l'image de $I$ par la rotation de centre $J$, d'angle $90^{\circ}$, en tournant dans le sens contraire des aiguilles d'une montre ?
e) Quelle est l'image de $J$ par la symétrie de centre $G$, suivie de la symétrie de centre $H$ ?
f) Quelle est l'image de $H$ par la translation de vecteur $\overrightarrow{GF}$ , suivie de la translation de vecteur $\overrightarrow{BF}$ ?
Exercice 18
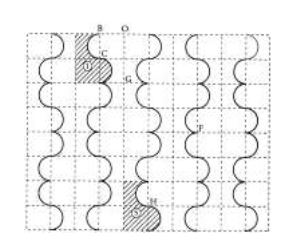
Un dessous de plat a la forme d'un rectangle, il est recouvert d'un carrelage comme le montre la figure.
1) a) Hachure l'image du motif 
dans la symétrie d'axe $(OG)$ et l'appeler $2.$
dans la symétrie d'axe $(OG)$ et l'appeler $2.$
b) Hachure l'image du motif $1$ dans la translation de vecteur $\overrightarrow{BF}$ et l'appeler $3$
c) Hachure l'image du motif $1$ dans la symétrie centrale de centre $C$ et l'appeler $4.$
2) Par quelle translation le motif va-t-il pour image le motif $5$ ?
Commentaires
Papa Abdourakhm... (non vérifié)
lun, 10/07/2024 - 01:42
Permalien
Solution des exercices sur l'isometrie et la transformation du p
Ajouter un commentaire