Exercices : Angle au centre - angle inscrit 3e
Classe:
Troisième
Exercice 1
$ABC$ est un triangle inscrit dans un cercle $(C)$ de centre $O$ et tel que les angles $\widehat{AOB}\ $ et $\ \widehat{BOC}$ sont adjacents.
$$mes\widehat{AOB}=50^{o}\;;\ mes\widehat{BOC}=100^{o}$$
Calculer la mesure de chacun des angles du triangle $ABC.$
Exercice 2
On considère un triangle $ABC$ isocèle en $A$, son cercle circonscrit $C(O\;;\ R)\ $ et $\ D$ un point diamétralement opposé à $B.$
1) Démontrer que $\widehat{ADB}=\widehat{ABC}$
2) Démontrer que $\widehat{DCA}\ $ et $\ \widehat{ADB}$ sont complémentaires.
Exercice 3
Tracer un cercle et un triangle $ABC$ dont les sommets appartiennent à ce cercle.
La bissectrice de l'angle $\widehat{BAC}$ coupe l'arc $\overset{\displaystyle\frown}{BC}$ en un point $I.$
Démontrer que le triangle $BIC$ est isocèle en $I.$
Exercice 4
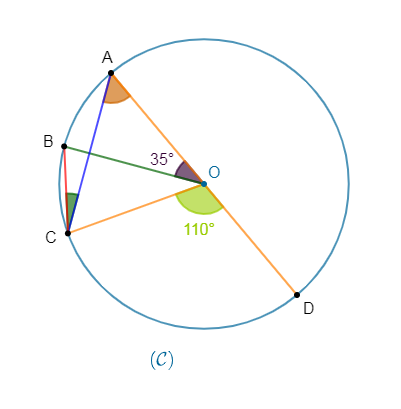
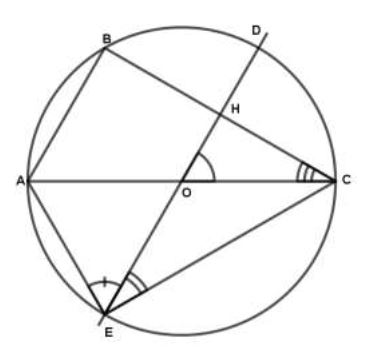
Soit la figure ci-dessous :
1) Quel est l'angle inscrit qui intercepte le même arc de cercle que $\widehat{AOB}$ ?
2) Calculer la mesure de $\widehat{ACB}$ puis la mesure de $\widehat{DAC}$. En déduire la mesure de $\widehat{AOC}\ ;;\ \widehat{AOB}=35^{o}\;;\ \widehat{COD}=110^{o}$
Exercice 5
Deux cercles sont sécants en $A\ $ et $\ B$. Une droite passant par $A$ coupe ces cercles en $M\ $ et $\ N$. Une autre droite passant par $A$ coupe ces cercles en $M'\ $ et $\ N'.$
Démontrer que les angles $\widehat{MBN}\ $ et $\ \widehat{M'BN'}$ ont même mesure.
Exercice 6
1) Soit un cercle $(\mathcal{C})$ de centre $O$ et de rayon $4\;cm$ et $[AD]$ un de ses diamètres.
a) D'un côté de la droite $(AD)$, construire le point $G$ tel que le triangle $ADG$ soit un triangle équilatéral.
b) De l'autre côté de la droite $(AD)$, placer le point $B$ du cercle $(\mathcal{C})$, tel que $AB=4\;cm.$
2) Démontrer que le triangle $OAB$ est équilatéral.
3) Justifier que les angles $\widehat{OAB}\ $ et $\ \widehat{ADG}$ sont égaux puis en déduire la position relative des droites $(AB)\ $ et $\ (DG).$
4) La droite $(BG)$ coupe $[AD]$ en $I\ $ et $\ (\mathcal{C})$ en $J.$
a) En utilisant le théorème de Thalès justifier que $\dfrac{IA}{ID}=\dfrac{1}{2}.$
b) Calculer la mesure de l'angle $\widehat{AJB}$
Exercice 7
Placer trois points $A\;,\ B\ $ et $\ C$ dans cet ordre sur un cercle $(\mathcal{C})$ de centre $O$ et de rayon $3\;cm$, de telle façon que les angles au centre $\widehat{AOB}\ $ et $\ \widehat{BOC}$ mesurent respectivement $40^{\circ}$ et $70^{\circ}.$
1) Calculer la mesure de tous les angles du triangle $ABC.$
2) Calculer la longueur des arcs $\overset{\displaystyle\frown}{AB}\ $ et $\ \overset{\displaystyle\frown}{AC}.$ (on donne $\pi\cong 3).$
3) Soit $M$ un point diamétralement opposés à $B.$ Calculer : $mes\widehat{BMC}\;;\ mes\widehat{AMC}\ $ et $\ mes\widehat{AMB}.$
Exercice 8 BFEM 2e groupe
Répondre par vrai ou faux en justifiant la réponse.
1) Si $a\ $ et $\ b$ sont deux angles inscrits qui interceptent le même arc de cercle alors $mes\;a= 2.mes\;b$
2) Si $x\ $ et $\ y$ représentent deux angles inscrits qui interceptent le même arc de cercle alors la mesure de $x$ est égale à la moitié de celle de $y.$
3) Si $(\mathcal{C})$ est un cercle de centre $O\ $ et $\ A\;,\ B\ $ et $\ M$ sont trois points de ce cercle tels que : $mes\widehat{AMB}=80^{\circ}$ alors l'angle $\widehat{AOB}=160^{\circ}.$
Exercice 9 BFEM 2006 2e groupe
1) Tracer un cercle $(\mathcal{C})$ de centre $I$ et de diamètre $[AB]$ tel que : $AB=8\;cm$, marque le point $E$ sur $(\mathcal{C})$ tel que : $AE=4\;cm.$
2) Quelle est la nature de chacun des triangles $ABE$ et $AEI\ ?$ Justifier chacune des réponses.
3) Déterminer la mesure de chacun des angles $\widehat{EAB}\ $ et $\ \widehat{BIE}.$
4) Soit $(d)$ la médiatrice du segment $[AB]$ ; la droite $(AE)$ coupe $(d)$ en $K.$
En posant : $\cos\widehat{BAE}=\cos\widehat{KAI}$, calculer les distances $AK\ $ et $\ KI.$
Exercice 10
Sur un demi-cercle de diamètre $[AA']$ et de rayon $4\;cm$, placer le point $B$ tel que : $\widehat{AOB}=30^{\circ}$ et appeler $H$, le projeté orthogonal de $B$ sur la droite $(AA').$
1) Faire une figure complète.
2) Calculer les longueurs : $OH\ $ et $\ HB.$
3) Trouver la mesure de l'angle $\widehat{AA'B}.$
Exercice 11
Soit $ABCD$ un quadrilatère inscriptible dans un cercle de centre $O$ et de rayon $3.5\;cm$ tel que : $mes\widehat{ADC}=65^{\circ}\ $ et $\ mes\widehat{DCB}=120^{\circ}.$
Calculer $mes\widehat{DAB}\ $ et $\ mes\widehat{ABC}.$ (On demande de faire la figure à main levée)
Exercice 12
$(\mathcal{C})$ est un cercle de centre $O$ et de rayon $r=3\;cm\ A\;,\ B\;,\ C\ $ et $\ D$ sont quatre points de $(\mathcal{C})$ tels que : $[AC]$ est un diamètre de $(\mathcal{C})\;;\ AB=r\;,\ D$ appartient au petit arc $\overset{\displaystyle\frown}{BC}\ $ et $\ mes\widehat{DCA}=50^{\circ}.$ Calculer la mesure de chacun des angles du quadrilatère $ABDC.$
Exercice 13
Soit $ABC$ un triangle.
$(\mathcal{C})$ est un cercle de centre $O$ passant par $B$ et par $C$ et recoupant le segment $[AB]$ en $D$ et le segment $[AC]$ en $E.$
1) Faire une figure.
2) Montrer que : $mes\widehat{BDC}=mes\widehat{CEB}$ et que : $mes\widehat{EBA}=mes\widehat{DCA}.$
Exercice 14
Définis les expressions suivantes :
Angle inscrit ; Angle au centre ; Angles associés.
Exercice 15
Les angles cités dans le tableau ci-dessous sont-ils des angles inscrits dans le cercle $\mathcal{C}(O\;;\ r)\ ?$
Si oui, quel est l'arc intercepté et nomme l'angle au centre associé.
Recopie et complète le tableau.
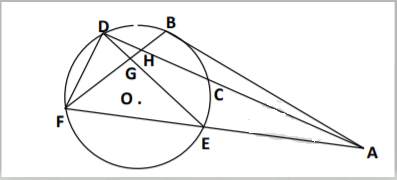
$$\begin{array}{|c|c|c|c|} \hline \text{Angles}&\text{Inscrit (oui/non)}&\text{Arc intercepté}&\text{Angle au centre associé}\\ \hline \widehat{EDF}& & &\\ \hline \widehat{ADE}& & &\\ \hline \widehat{DAF}& & &\\ \hline \widehat{BFA}& & &\\ \hline \widehat{DEF}& & &\\ \hline \end{array}$$
Exercice 16
Construis un cercle $\mathcal{C}(O\;;\ r)$ et marque sur $(\mathcal{C})$ les points $A\;,\ B\ $ et $\ E$ tels que $A\ $ et $\ E$ soient diamétralement opposés et $\widehat{AEB}=30^{\circ}.$
1) Calcule l'angle $\widehat{AOB}.$
2) Montre que le triangle $AOB$ est équilatéral.
Exercice 17
Construis un triangle $ABC$ puis trace le cercle $(\mathcal{C})$ circonscrit à ce triangle.
Soit $O$ le centre de ce cercle et $M$ le symétrique de $B$ par rapport à $O.$
1) a) Donne la relation entre les mesures des angles suivants :
$\widehat{MOC}\ $ et $\ \widehat{MBC}.$
$\widehat{MOA}\ $ et $\ \widehat{MBA}.$
b) Déduis-en $\widehat{ABC}$ en fonction de $\widehat{AOC}$
2) a) Compare $\widehat{BAM}\ $ et $\ \widehat{BCM}.$
b) Déduis-en la nature de chacun des triangles $ABM\ $ et $\ MCB.$
Exercice 18
On considère un cercle $(\mathcal{C})$ de centre $O$ et $A$, $M$ et $B$ trois points distincts de $(\mathcal{C})$ non diamétralement opposés deux à deux.
1) Justifie que les triangles $AOB\;,\ AOM\ $ et $\ BOM$ sont isocèles.
2) Exprime la mesure de l'angle $\widehat{AOB}$ en fonction de la mesure de l'angle $\widehat{OAB}.$
3) On note $\widehat{OAB}=a\;;\ \widehat{OMA}=b\ $ et $\ \widehat{OBM}=c.$
a) Exprime la somme des angles du triangle $AMB$ en fonction de $a\;,\ b\ $ et $\ c.$
b) En utilisant la propriété de la somme des angles dans un triangle, exprime $2a$ en fonction de $b\ $ et $\ c.$
c) Déduis du b) et du 2) l'expression de l'angle $\widehat{AOB}$ en fonction $b\ $ et $\ c.$
d) Déduis, en factorisant par $2$, l'expression de l'angle $\widehat{AOB}$ en fonction de l'angle inscrit $M$
Exercice 19
Sur la figure ci-dessous,
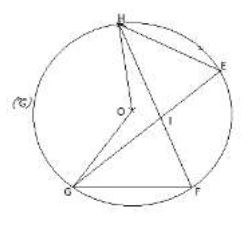
les points $E\;,\ F\;,\ G\ $ et $\ H$ sont sur le cercle $(\mathcal{C})$ de centre $O.$
Les droites $(FH)\ $ et $\ (EG)$ sont sécantes au point $I.$
$\widehat{HOG}=130^{\circ}\ $ et ̂$\ \widehat{EHF}=40^{\circ}$
Calcule la mesure de chaque angle du triangle $FGI.$
Justifier chaque réponse
Exercice 20
On considère la figure ci-dessous dans laquelle :
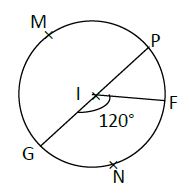
Les points $P\;,\ F\;,\ N\;,\ M\ $ et $\ G$ appartiennent au cercle de centre $I.$
Le segment $[GP]$ est un diamètre du cercle et le point $F$ appartient à la médiatrice de $[MG]$
1) Quelle est la nature du triangle $GNP\ ?$
2) Démontre que le triangle $MGF$ est un triangle équilatéral.
3) Calcule la mesure de l'angle $\widehat{GNF}.$
Exercice 21
$ABC$ est un triangle rectangle en $B$ tel que $AB=5\;cm\;;\ \widehat{BAC}=30^{\circ}.$
1) Construis $ABC.$
2) Construis le cercle circonscrit au triangle $ABC$ son centre est $O.$
3) La hauteur $(BI)$ de $ABC$ coupe $(AC)$ en $I$ et le cercle en $J.$
Détermine $\widehat{BJC}$
4) Calcule les mesures des angles du triangle $BOC$
5) Calcule les mesures des angles du triangle $ABJ.$
Exercice 22
On considère la figure ci-dessous
où le cercle de centre $O$ a pour diamètre $AC=10\;cm\;;\ B$ sur le cercle tel que $AB=5\;cm.$
1) Quelle est la nature du triangle $ABC\ ?$ Justifie ta réponse.
2) Calcule la valeur exacte de la distance $BC.$
3) Calcule la mesure de l'angle $\widehat{ACB}.$
4) La parallèle à la droite $(AB)$ passant par $O$ coupe le segment $[BC]$ en $H$ et le cercle en deux points $D\ $ et $\ E$ tels que $CD<CE.$
a) Calcule la mesure de l'angle $\widehat{HOC}.$
b) Déduis-en la mesure de l'angle $\widehat{DEC}$ et celle de l'angle $\widehat{DEA}.$
Exercice 23
Soit $SUD$ un triangle tel que $SU=6\;cm$, $\widehat{SUD}=60^{\circ}\ $ et $\ \widehat{DSU}=45^{\circ}\;,\ (\mathcal{C})$ est le cercle de centre $O$ circonscrit au triangle $SUD.$
1) Fais une figure.
2) Montre que $\widehat{UOD}=90^{\circ}$
3) Soit $A$ le point diamétralement opposé à $D.$
a) Calcule $\widehat{SAD}.$
b) Montre que $(SU)$ est la bissectrice de $\widehat{DSA}$
4) Soit $M$ un point de l'arc $\overset{\displaystyle\frown}{DU}$
a) Quel est l'angle au centre associé à $\widehat{DMU}\ ?$
b) En déduis la mesure de l'angle $\widehat{DMU}.$
Exercice de Synthèse
L'angle inscrit est égal :
a) $2$ angle au centre
b) $\dfrac{1}{2}$ angle au centre
c) angle au centre
$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

Commentaires
Aminata sow (non vérifié)
mar, 04/27/2021 - 20:31
Permalien
Merci
MOUHAMED ndiaye (non vérifié)
mar, 05/04/2021 - 02:48
Permalien
Correction d exercice n19
Aly kante (non vérifié)
dim, 06/13/2021 - 08:50
Permalien
mathématiques
gharbi (non vérifié)
jeu, 10/20/2022 - 13:15
Permalien
bien
Anonyme (non vérifié)
lun, 12/19/2022 - 22:47
Permalien
Correction de l'exercice n 22
Ajouter un commentaire