Devoir n° 3 maths - 4e
Classe:
Quatrième
Exercice 1
Sur la figure ci-dessous on a représenté la position de cinq (5) villages $A\;,\ B\;,\ C\;,\ E\ $ et $\ F$
Le village $E$ est équidistant des villages $A\ $ et $\ C.$
Le village $F$ est équidistant des villages $B\ $ et $\ C.$
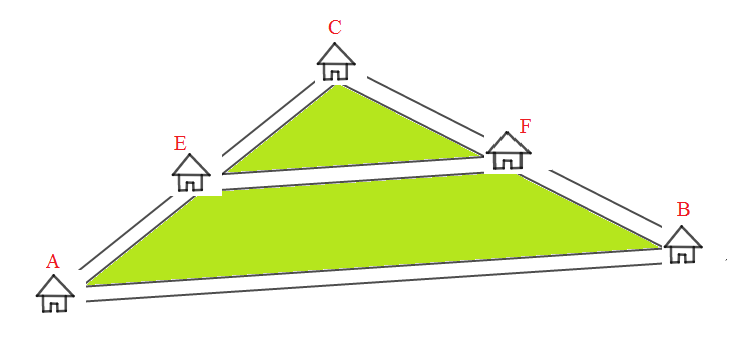
Partant du village $A$, Amadou a mis une demi-heure de marche pour rejoindre le village $B$ avec une vitesse de $2\;m.s^{-1}$
Au même moment, Badou part du village $E$ pour rejoindre le village $F$, à la même vitesse.
1) Calcule la distance qui sépare les villages $A\ $ et $\ B.$
2) Calcule le temps mis par Badou pour rejoindre le village $F.$
3) Énonce la propriété géométrique utilisée.
Exercice 2
Développer, réduire et ordonner les expressions suivantes.
$F=\left(\dfrac{5x}{2}-9\right)^{2}$
$G=\left(\dfrac{4x}{9}-\dfrac{2}{5}\right)\left(\dfrac{4x}{9}+\dfrac{2}{5}\right)$
$I=\left(5\dfrac{x}{3}-\dfrac{1}{2}\right)^{2}$
2) Factorisons les expressions suivantes.
$E=\left(\dfrac{4x}{5}-\dfrac{1}{7}\right)^{2}-\left(\dfrac{2x}{5}+\dfrac{1}{2}\right)^{2}$
$F=\left(2x-\dfrac{2}{3}\right)^{2}-9\left(\dfrac{3}{2}x+1\right)^{2}$
Exercice 3
On considère les encadrements suivants :
$$1.20<x<1.21\ \text{ et }\ 3.90<y<3.91$$
1) Donner un encadrement de $\dfrac{xy}{3}\ $ à $10^{-2}$ prés.
2) Donner un encadrement de $\left(\dfrac{1}{2}x-\dfrac{2}{3}y\right)\ $ à $10^{-2}$ prés.
3) Donner un encadrement de $\left(\dfrac{y-2}{x}\right)\ $ à $10^{-1}$ prés puis en déduire sa valeur approchée par excès.
$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction Devoir}}\end{array}$
Auteur:
Diny Faye

Commentaires
Anonyme (non vérifié)
ven, 04/30/2021 - 14:17
Permalien
ok
khadija dia (non vérifié)
lun, 03/18/2024 - 18:35
Permalien
pas satisfait
donald qui a un... (non vérifié)
dim, 06/02/2024 - 22:14
Permalien
pas mal le devoir mais il
Ajouter un commentaire