Corrigé Devoir n°32 - Ts2

On considère dans $\mathbb{C}$ l'équation $-z^{3}+(4+\mathrm{i})z^{2}+(8+6\mathrm{i})z+4+28\mathrm{i}=0.$

 

1) Montrer que cette équation admet une solution imaginaire pure que l'on notera $\alpha.$

 

Soit $\alpha=\mathrm{i}b$ avec $b\ \in\ \mathbb{R}^{\ast}$ une solution de $(E).$ On a alors :

 

$\begin{array}{rcl} -(\mathrm{i}b)^{3}+(4+\mathrm{i})(\mathrm{i}b)^{2}+(8+6\mathrm{i})(\mathrm{i}b)+4+28\mathrm{i}=0 &\Leftrightarrow&  \mathrm{i}b^{3}-b^{2}(4+\mathrm{i})+8\mathrm{i}b-6b+4+28\mathrm{i}=0 \\ \\ &\Leftrightarrow& -4b^{2}-6b+4+\mathrm{i}(b^{3}-b^{2}+8b+28)=0 \\ \\ &\Leftrightarrow& \left\lbrace\begin{array}{rcl} -4b^{2}-6b+4 & = & 0\quad(1) \\ \\ b^{3}-b^{2}+8b+28 &=& 0\quad(2)\end{array}\right.\end{array}$

 

En résolvant l'équation (1) on obtient $b=-2$ ou $b=\dfrac{1}{2}$

On vérifie aisément que seule la valeur $b=-2$ est solution de l'équation (2).

 

Par suite la solution imaginaire pure est $\boxed{\alpha=-2\mathrm{i}}$

 

2) Déterminons les autres solutions $\beta$ et $\gamma$ de l'équation.

 

Passons par la méthode de Hörner. Comme $\alpha=-2\mathrm{i}$ est solution de $(E)$ on a alors :

 

$$\begin{array}{|c|c|c|c|c|} \hline & -1 & 4+\mathrm{i} & 8+6\mathrm{i} & 4+28\mathrm{i} \\ \hline -2\mathit{i} & ||| & 2\mathrm{i} & 6-8\mathrm{i} & -4-28\mathrm{i} \\ \hline & -1 & 4+3\mathrm{i} & 14-2\mathrm{i} & 0 \\\hline  \end{array}$$

 

$(E): (z+2\mathrm{i})(-z^{2}+(4+3\mathrm{i})z+14-2\mathrm{i})=0$

 

Résolvons l'équation $-z^{2}+(4+3\mathrm{i})z+14-2\mathrm{i}=0$

 

On a $\Delta=(4+3\mathrm{i})^{2}+4(14-2\mathrm{i})=63+16\mathrm{i}\;\in\;\mathbb{C}-\mathbb{R}$

 

Cherchons une racine carrée de $\Delta.$

 

Soit $\delta=a+\mathrm{i}b$ une racine de $\Delta$ donc $\delta^{2}=\Delta$ On a alors :

 

$$\left\lbrace\begin{array}{lcl} |\delta|^{2} &=& |\Delta| \\ \delta^{2} &=& \Delta \end{array}\right.\;\ \Leftrightarrow\;\ \left\lbrace\begin{array}{lcl} a^{2}+b^{2} &=&\sqrt{63}^{2}+65^{2} \\ (a+\mathrm{i}b)^{2} &=& 63+16\mathrm{i} \end{array}\right.$$ 

 

donc $$\left\lbrace\begin{array}{lcl} a^{2}+b^{2} &=& 65 \\ \\ a^{2}-b^{2}+2\mathrm{i}ab &=& 63+16\mathrm{i} \end{array}\right.$$ 

 

Par identification on a : $$\left\lbrace\begin{array}{llll} a^{2}+b^{2} &=& 65 & (1) \\ a^{2}-b^{2} &=& 63 & (2) \\ ab &=& 8 & (3) \end{array}\right.$$

 

En combinant (1) et (2) on obtient $a=\pm8$ et $b=\pm1.$ Et comme $ab=8$ donc $a$ et $b$ ont même signe.

 

Par suite $a=8$ et $b=1$ ou $a=-8$ et $b=-1.$

 

Prenons $\delta=8+\mathrm{i}$ Donc $\boxed{\beta=6+2\mathrm{i}}$ et $\boxed{\gamma=-2+\mathrm{i}}$

 

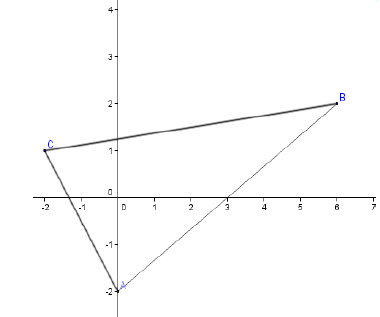
3) Soit $A\;,\ B$ et $C$ les points d'affixes respectives $-2\mathrm{i}\;,\ 6+2\mathrm{i}$ et $-2+\mathrm{i}$

 

a) Plaçons les points $A\;,\ B$ et $C.$

 

 

b) Calculons $\dfrac{\beta-\alpha}{\gamma-\alpha}$

 

On a $\dfrac{\beta-\alpha}{\gamma-\alpha} =\dfrac{6+2\mathrm{i}+2\mathrm{i}}{-2+\mathrm{i}+2\mathrm{i}}=\dfrac{6+4\mathrm{i}}{-2+3\mathrm{i}}=-2\mathrm{i}.$

 

$\boxed{\dfrac{\beta-\alpha}{\gamma-\alpha}=-2\mathrm{i}}$

 

c) Déduisons la nature du triangle $ABC.$ On a :

 

$\dfrac{\beta-\alpha}{\gamma-\alpha}=\dfrac{z_{B}-z_{A}}{z_{C}-z_{A}}=-2\mathrm{i}$

 

$\left|\dfrac{z_{B}-z_{A}}{z_{C}-z_{A}}\right|=|-2\mathrm{i}|=2\neq 1$

 

donc $AB\neq AC\ (1)$

 

$arg\left(\dfrac{z_{B}-z_{A}}{z_{C}-z_{A}}\right)=arg(-2\mathrm{i})=-\dfrac{\pi}{2}[2\pi]$

 

donc $(\overrightarrow{AC}\;,\ \overrightarrow{AB})=-\dfrac{\pi}{2}[2\pi]\ (2)$

 

(1) et (2) $\Longrightarrow ABC$ est un triangle rectangle en $A.$

Soit $z=-8\sqrt{3}+8\mathrm{i}\quad;\quad u=(\sqrt{6}-\sqrt{2})+\mathrm{i}(\sqrt{6}+\sqrt{2}$

 

1) Calculons le module et un argument de $z.$

 

On a $|z|=\sqrt{(-8\sqrt{3})^{2}+8^{2}}=16$

 

Soit $\theta$ un argument de $z$ on a alors :

 

$$\left\lbrace\begin{array}{lcl} \cos\theta &=& -\dfrac{8\sqrt{3}}{16} \\ \\ \sin\theta &=& \dfrac{8}{16}\end{array}\right.\;\ \Leftrightarrow\;\ \left\lbrace\begin{array}{lcl} \cos\theta &=& -\dfrac{\sqrt{3}}{2}\\ \\ \sin\theta &=& \dfrac{1}{2}\end{array}\right.$$

 

Donc $\theta=\dfrac{5\pi}{6}$ est un argument de $z.$

 

$\boxed{|z|=16}$ et $\boxed{arg(z)=\dfrac{5\pi}{6}}$

 

2) Déterminons sous forme trigonométrique, les racines carrées de $z.$

 

On a $z=16\mathrm{e}^\mathrm{i}\dfrac{5\pi}{6}$

 

Soit $a$ tel que $a^{2}=z$ Posons $a=r\mathrm{e}^{\mathrm{i}\alpha}$ On a :

 

$\begin{array}{rcl} a^{2}=z &\Leftrightarrow &(r\mathrm{e}^{\mathrm{i}\alpha})^{2}=16\mathrm{e}^{\mathrm{i}\dfrac{5\pi}{6}} \\ \\ &\Leftrightarrow & r^{2}\mathrm{e}^{\mathrm{i}2\alpha}=16\mathrm{e}^{\mathrm{i}\dfrac{5\pi}{6}}\\ \\ &\Leftrightarrow & \left\lbrace\begin{array}{rcl} r^{2} &=& 16 \\ \\ 2\alpha &=& \dfrac{5\pi}{6}+2k\pi\;,\ k\in\mathbb{Z} \end{array}\right. \\ \\ &\Leftrightarrow & \left\lbrace\begin{array}{rcl} r &=& 4 \\ \\ \alpha &=& \dfrac{5\pi}{12}+k\pi\;,\;k\in\mathbb{Z} \end{array}\right.\end{array}$

 

Donc les racines carrées de $z$ sont les $a_{k}=4\mathrm{e}^{\mathrm{i}(\frac{5\pi}{12}+k\pi)}$ avec $k=0\;;\ 1$

 

D'où $a_{0}=4\mathrm{e}^{\mathrm{i}(\frac{5\pi}{12})}$ et $a_{1}=4\mathrm{e}^{\mathrm{i}(\frac{17\pi}{12})}$ sont les racines carrées de $z.$

 

Sous forme trigonométrique on a :

 

$\boxed{a_{0}=4\left(\cos\dfrac{5\pi}{12}+\sin\dfrac{5\pi}{12}\right)}$ $\boxed{a_{1}=4\left(\cos\dfrac{17\pi}{12}+\mathrm{i}\sin\dfrac{17\pi}{12}\right)}$

 

3) Calculons $u^{2}$ puis exprimons les racines carrées de $z$ sous forme algébrique.

 

Calculons $u^{2}$

 

On a :

 

$\begin{array}{rcl} u^{2}&=& [(\sqrt{6}-\sqrt{2})+\mathrm{i}\sqrt{6}+\sqrt{2})]^{2} \\ \\ &=& (\sqrt{6}-\sqrt{2})^{2}-(\sqrt{6}+\sqrt{2})^{2}+2\mathrm{i}(\sqrt{6}-\sqrt{2})(\sqrt{6}+\sqrt{2}) \\ \\ &=& 6+2-2\sqrt{12}-6-2-2\sqrt{12}+2(6-2)\mathrm{i} \\ \\ &=& -4\sqrt{12}+8\mathrm{i} \\ \\ &=& -8\sqrt{3}+8\mathrm{i} \end{array}$

 

Alors $\boxed{u^{2}=-8\sqrt{3}+8\mathrm{i}}$

 

Exprimons les racines carrées de $z$ sous forme algébrique.

 

On a $u^{2}=-8\sqrt{3}+8\mathrm{i}=z$ donc $u=(\sqrt{6}-\sqrt{2})+\mathrm{i}(\sqrt{6}+\sqrt{2})$ est une racine carrée de $z$

 

et donc on obtient l'autre en multipliant $u$ par $-1$ qui est la deuxième racine carrée de l'unité.

 

Par suite l'autre racine est $u'=-(\sqrt{6}-\sqrt{2})-\mathrm{i}(\sqrt{6}+\sqrt{2})$ Sous forme algébrique

 

On a :

 

$\boxed{u=(\sqrt{6}-\sqrt{2})+\mathrm{i}(\sqrt{6}+\sqrt{2})}$ 

 

$\boxed{u'=-(\sqrt{6}-\sqrt{2})+\mathrm{i (\sqrt{6}+\sqrt{2})}}$

 

4) Déduisons la valeur exacte de $\cos\dfrac{5\pi}{6}$ et $\sin\dfrac{5\pi}{6}$

 

On a $u=a_{0}$ donc,

$\begin{array}{rcl} 4\left(\cos\dfrac{5\pi}{12}+\mathrm{i}\sin\dfrac{5\pi}{12}\right) &=& (\sqrt{6}-\sqrt{2})\mathrm{i}(\sqrt{6}\sqrt{2}) \\ \\ &\Leftrightarrow& \cos\dfrac{5\pi}{12}+\mathrm{i}\sin\dfrac{5\pi}{12} \left(\dfrac{\sqrt{6}-\sqrt{2}}{4}\right)+\mathrm{i}\left(\dfrac{\sqrt{6}+\sqrt{2}}{4}\right) \\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl} \cos\dfrac{5\pi}{12} &=& \dfrac{\sqrt{6}-\sqrt{2}}{4} \\ \\ \sin\dfrac{5\pi}{12} &=& \dfrac{\sqrt{6}+\sqrt{2}}{4}\end{array}\right. \end{array}$

Le plan complexe est rapporté à un repère orthonormal $(O\;,\ \vec{u}\ ,\ \vec{v})$

 

On appelle $A\;,\ B$ et $C$ les points d'affixes respectives

 

$z_{A}=-1+3\mathrm{i}\quad;\quad z_{B}=-2$ et $z_{C}=-\dfrac{3-3\mathrm{i}}{2}$

 

Soit $f$ l'application du plan privé de $A$ dans le plan qui, à tout point $M$ d'affixe $z$ distincte de $z_{A}$ associe le point $M$ d'affixe $z'$ définie par : $z'=\dfrac{z+2}{z+1-3\mathrm{i}}$

 

1) Factorisons $z^{2}-3\mathrm{i}z-2$ en remarquant que $z=\mathrm{i}$ en est une solution,

 

puis résolvons l'équation $(E)$ : $z^{2}-3\mathrm{i}z-2=0$

 

Factorisons $z^{2}-3\mathrm{i}z-2$ en remarquant que $z=\mathrm{i}$ en est une solution.

 

Comme $z_{1}=\mathrm{i}$ est solution de $z^{2}-3\mathrm{i}z-2-2$ alors si $z_{1}$ désigne l'autre racine on a :

 

$z_{1}z_{2}=-2$ D'où $z_{2}=-\dfrac{2}{\mathrm{i}}=2\mathrm{i}$

 

Par suite $\boxed{z^{2}-3\mathrm{i}z-2=(z-\mathrm{i})(z-2\mathrm{i})}$

 

résolvons l'équation $(E)$ : $z^{2}-3\mathrm{i}z-2=0$

 

$\begin{array}{rcl} z^{2}-3\mathrm{i}z-2=0 &\Leftrightarrow& (z-\mathrm{i})(z-2\mathrm{i})=0 \\ \\ &\Leftrightarrow& z=\mathrm{i}\quad ou\quad z=2\mathrm{i} \\ \\ &\Leftrightarrow& \boxed{S={\mathrm{i\;;\ 2\mathrm{i}}}} \end{array}$

 

2) Déterminons les affixes des points invariants par $f$. (Un point est invariant lorsque $z=z'$)

 

$\begin{array}{rcl} z\; \text{ est invariant par }\; f &\Leftrightarrow & f(z)=z \\ \\ &\Leftrightarrow & \dfrac{z+2}{z+1-3\mathrm{i}}=z \\ \\ &\Leftrightarrow & z+2=z^{2}+z-3\mathrm{i}z \\ \\ &\Leftrightarrow & -z^{2}+3\mathrm{i}z-2=0 \\ \\ &\Leftrightarrow & z^{2}-3\mathrm{i}z+2=0\\ \\ &\Leftrightarrow & z=\mathrm{i}\quad \text{ou} \quad z=2\mathrm{i}\end{array}$

 

Par suite les points invariants ont pour affixes $\boxed{z=\mathrm{i}}$ et $\boxed{z=2\mathrm{i}}$

 

3) Déterminons l'ensemble des points $M$ du plan tels que $M'$ appartienne au cercle de centre $O$ et de rayon $1.$

 

On a

 

$\begin{array}{rcl} M'\;\in\;C(O\;,\ 1) &\Leftrightarrow& OM'=1 \\ \\ &\Leftrightarrow& |z'-z_{0}|=1 \\ \\ &\Leftrightarrow& |z'|=1 \\ \\ &\Leftrightarrow& \left|\dfrac{z+2}{z+1-3\mathrm{i}}\right|=1 \\ \\ &\Leftrightarrow& |z+2|=|z+1-3\mathrm{i}| \\ \\ &\Leftrightarrow& |z-(-2)|=|z (1+3\mathrm{i})| \\ \\ &\Leftrightarrow&  |z-z_{B}|=|z-z_{A}|\\ \\ &\Leftrightarrow& MB=MA\\ \\ &\Leftrightarrow& M \text{appartient à la médiatrice de} [AB]\end{array}$

 

Par suite l'ensemble des points $M$ du plan tels que $M'$ appartienne au cercle de centre $O$ et de rayon 1 est la médiatrice du segment $[AB].$

 

4) En posant $z=x+\mathrm{i}y$, déterminons $\Im(z')$ en fonction de $x$ et $y$.

 

En déduire l'ensemble des points $M$ du plan tels que $M'$ appartienne à l'axe des abscisses. déterminons $\Im(z')$ en fonction de $x$ et $y$.

 

On a :

 

$\begin{array}{rcl} z' &=& \dfrac{z+2}{z+1-3\mathrm{i}} \\ \\ &=& \dfrac{x+\mathrm{i}y+2}{x+\mathrm{i}+1-3\mathrm{i}} \\ \\ &=& \dfrac{x+2+\mathrm{i} y}{x+1+\mathrm{i}(y-3)} \\ \\ &=& \dfrac{(x+2 \mathrm{i} y)(x+1-\mathrm{i})(y+3)}{(x+1)^{2}+(y-3)^{2}} \\ \\ &=&\dfrac{(x+2+\mathrm{i} y)(x+1-\mathrm{i} y-3\mathrm{i})}{(x+1)^{2}+(y-3)^{2}} \\ \\ &=&\dfrac{x^{2}+x-\mathrm{i} xy-3\mathrm{i} x+2x+2-2\mathrm{i} y-6\mathrm{i}\mathrm{i} xy+\mathrm{i} y+y^{2}+3y}{(x+1)^{2}+(y-3)^{2}} \\ \\ &=& \dfrac{x^{2}+y^{2}+3x+3y+2}{(x+1)^{2}(y-3)^{2}}\mathrm{i}\dfrac{-3x+y-6}{(x+1)^{2}+(y-3)^{2}} \end{array}$

 

Par identification on a $\boxed{\Im(z')=\dfrac{-3x+y-6}{(x+1)^{2}+(y-3)^{2}}}$

 

Déduisons l'ensemble des points $M$ du plan tels que $M'$ appartienne à l'axe des abscisses.

On a :

 

$\begin{array}{rcl} M\ \in\;(Ox) &\Leftrightarrow& \Im(z')=0 \\ \\ &\Leftrightarrow& \dfrac{-3x+y-6}{(x+1)^{2}+(y-3)^{2}}=0 \\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl} -3x+y-6 &=& 0 \\ (x+1)^{2}+(y-3)^{2} & \neq & 0 \end{array}\right. \\ \\ &\Leftrightarrow& \left\lbrace\begin{array}{rcl} -3x+y-6 &=& 0 \\ (x\;,\ y) &\neq & (-1\;,\ 3) \end{array}\right. \end{array}$

 

Par suite l'ensemble des points $M$ du plan tels que $M'$ appartienne à l'axe des abscisses est la droite $(D)\ :\ -3x+y-6=0$ privée du point $A.$

Soit $g$ la fonction définie par $$g(x)=\left\lbrace\begin{array}{lll} x\sqrt{\left|\dfrac{x+1}{x}\right|} &\text{si} & x<0 \\ \\ \dfrac{x^{3}-x^{2}}{x^{2}+1} & \text{si} & x\geq 0 \end{array}\right.$$

 

1) Montrons que $g$ est définie sur $\mathbb{R}$.

 

Écrivons $g$ sans barres de valeur absolue.

 

Montrons que $g$ est définie sur $\mathbb{R}$

 

Posons $g_{1}(x)=x\sqrt{\left|\dfrac{x+1}{x}\right|}\quad\text{si}\quad x<0$

 

$\begin{array}{rcl} g_{1}(x)\exists &\Leftrightarrow&\left\lbrace\begin{array}{rcl} x &<& 0 \\ \\ \dfrac{x+1}{x} &\geq & 0 \end{array}\right. \\ \\ &\Leftrightarrow& \left\lbrace\begin{array}{rcl} x &<& 0 \\  x &\in &\mathbb{R}\setminus\{0\} \end{array} \right. \\ \\ &\Leftrightarrow& Dg_{1}=]-\infty\;;\ 0[ \end{array}$

 

Posons $g_{1}(x)=\dfrac{x^{3}-x^{2}}{x^{2}+1}\quad \text{si}\quad x\geq 0$

 

$\begin{array}{rcl} g_{2}(x)\exists &\Leftrightarrow& \left\lbrace\begin{array}{rcl} x & \geq & 0 \\ x^{2}+1 &\neq & 0 \end{array}\right. \\ \\ &\Leftrightarrow& \left\lbrace\begin{array}{rcl} x &\geq & 0  \\ x &\in & \mathbb{R}  \end{array}\right. \\ \\ &\Leftrightarrow& Dg_{2}=[0\;;\ +\infty[ \end{array}$

 

Par suite $Dg=Dg_{1}\cup Dg_{2}=]-\infty\;;\ 0[\cup[0\;;\ +\infty[=\mathbb{R}.$

 

$\boxed{Dg=\mathbb{R}}$

 

Écrivons $g$ sans barres de valeur absolue.

 

Posons $\dfrac{x+1}{x}=0$ Donc on a  $x=-1\ $ et $\ x\neq 0$

 

$$\begin{array}{|c|lcr|lcr|} \hline x&-\infty& & -1 &  & & 0 \\ \hline x+1&  &-&  &  &+&   \\ \hline x&   &-&  &  &-&   \\ \hline \dfrac{x+1}{x}&   &+&   &   &-&   \\ \hline \left|\dfrac{x+1}{x}\right|&   &\dfrac{x+1}{x}&   &  &-\dfrac{x+1}{x}&  \\ \hline \end{array}$$

 

$$g(x)=\left\lbrace\begin{array}{lll} x\sqrt{\dfrac{x+1}{x}} & \text{si} & x\;\in]-\infty\;;\ -1] \\ \\ \sqrt{\dfrac{-x-1}{x}} & \text{si} & x\;\in]-1\;;\ 0[ \\ \\ \dfrac{x^{3}-x^{2}}{x^{2}+1} & \text{si} & x\in[0\;;\ +\infty[\end{array}\right.$$

 

2) Étudions la continuité et la dérivabilité de $g$ en 0 et en -1

 

Continuité en 0

 

Comme $0\in\;Dg$ on a $g(0)=\dfrac{0^{3}-0^{2}}{0^{2}+1}=0$

 

$\lim\limits_{x\rightarrow 0^{+}}g(x)=\lim\limits_{x\rightarrow 0^{+}}\dfrac{x^{3}-x^{2}}{x^{2}+1}=0=g(0)$

 

Par suite $g$ est continue à droite de $0$

 

$\lim\limits_{x\rightarrow 0^{-}}g(x)=\lim\limits_{x\rightarrow 0^{-}}x\sqrt{\dfrac{-x-1}{x}}.$

 

Or $\lim\limits_{x\rightarrow 0^{-}}\dfrac{-x-1}{x}=\dfrac{-1}{0^{-}}=+\infty$

 

Donc par composée on a $\lim\limits_{x\rightarrow 0^{-}}\sqrt{\dfrac{-x-1}{x}}=+\infty$

 

De plus $\lim\limits_{x\rightarrow 0^{-}}x=0$ donc par produit nous avons une forme indéterminée.

 

Levons l'indétermination

 

On a

 

$$\begin{array}{rcl} \lim\limits_{x\rightarrow 0^{-}}x\sqrt{\dfrac{-x-1}{x}} &=& \lim\limits_{x\rightarrow 0^{-}}x\sqrt{\dfrac{-x+1}{-x}} \\ \\ &=& \lim\limits_{x\rightarrow 0^{-}}\dfrac{x}{\sqrt{-x}}\times\sqrt{x+1} \\ \\ &=& \lim\limits_{x\rightarrow 0^{-}}\sqrt{-x}\times\sqrt{x+1} \\ \\ &=& 0\times 1 \\ \\ &=& 0 \end{array}$$

 

Donc $\lim\limits_{x\rightarrow 0^{-}}g(x)=0=g(0).$

 

Par suite $g$ est continue à gauche de 0

 

Conclusion :

 

On a $\lim\limits_{x\rightarrow 0^{-}}g(x)=\lim\limits_{x\rightarrow 0^{+}}g(x)=g(0)=0$

 

donc $g$ est continue en $0.$

 

Continuité en $-1$

 

Comme $-1\;\in\;Dg$ on a $g(-1)=-1\times\sqrt{\dfrac{0}{-1}}=0$

 

$\lim\limits_{x\rightarrow -1^{+}}g(x)=\lim\limits_{x\rightarrow -1^{+}}x\sqrt{\dfrac{-x-1}{x}}=0=g(-1).$

 

Par suite $g$ est continue à droite de -1

 

$\lim\limits_{x\rightarrow -1^{+}}g(x)=\lim\limits_{x\rightarrow -1^{+}}x\sqrt{\dfrac{x+1}{x}}=0=g(-1).$

 

Par suite $g$ est continue à gauche de -1

 

Conclusion : 

On a $\lim\limits_{x\rightarrow -1^{+}}g(x)=\lim\limits_{x\rightarrow -1^{+}}=g(-1)=0$

 

donc $g$ est continue en $-1$

 

Dérivabilité en $0$

 

$$\begin{array}{rcl} \lim\limits_{x\rightarrow 0^{-}}\dfrac{g(x)-g(0)}{x-0} &=& \lim\limits_{x\rightarrow 0^{-}}\dfrac{g(x)}{x} \\ \\ &=& \lim\limits_{x\rightarrow 0^{-}}x\sqrt{\dfrac{-x-1}{x}} \\ \\ &=& \lim\limits_{x\rightarrow 0^{-}}\dfrac{1}{\sqrt{-x}}\times\sqrt{x+1} \\ \\ &=& \dfrac{1}{0^{+}} \nonumber \\ &=& +\infty \end{array}$$

 

$\boxed{\lim\limits_{x\rightarrow 0^{-}}\dfrac{g(x)-g(0)}{x-0}=+\infty}$

 

Par suite $g$ n'est pas dérivable à droite de $0$ et par conséquent $(Cg)$ admet une tangente verticale en $0^{+}$

 

$$\begin{array}{rcl} \lim\limits_{x\rightarrow 0^{+}}\dfrac{g(x)-g(0)}{x-0} &=& \lim\limits_{x\rightarrow 0^{+}}\dfrac{g(x)}{x}\\ \\ &=& \lim\limits_{x\rightarrow 0^{+}}\dfrac{x^{3}-x^{2}}{x(x^{2}+1} \\ \\ &=& \lim\limits_{x\rightarrow 0^{+}}\dfrac{x^{2}-x}{x^{2}+1} \\ \\ &=& 0 \end{array}$$

 

$\boxed{\lim\limits_{x\rightarrow 0^{+}}\dfrac{g(x)-g(0)}{x-0}=-1}$

 

Par suite $g$ est dérivable à gauche de $0$ et par conséquent $(Cg)$ admet $0^{+}$ une tangente $(D)$ d'équation $y=f'(0)x+0=0.$ Donc $(D)\ :\ y=0$

 

Conclusion $g$ n'est pas dérivable en $0.$

 

Par conséquent :

 

$(C_{g})$ admet une demi-tangente verticale en $0^{+}$

 

$(C_{g})$ admet $0^{+}$ une tangente $(D)$ d'équation $(D)$ : $y=0$

 

Dérivabilité en $-1$

 

$$\begin{array}{rcl} \lim\limits_{x\rightarrow -1^{-}}\dfrac{g(x)-g(-1)}{x+1} &=& \lim\limits_{x\rightarrow -1^{-}}\dfrac{g(x)}{x-1} \\ \\ &=& \lim\limits_{x\rightarrow -1^{-}}\dfrac{x}{x+1}\times\sqrt{\dfrac{x+1}{x}} \\ \\ &=& \lim\limits_{x\rightarrow -1^{-}}\sqrt{\left(\dfrac{x}{x+1}\right)^{2}\times\dfrac{x+1}{x}} \\ \\ &=& \lim\limits_{x\rightarrow -1^{-}}\sqrt{\dfrac{x}{x+1}} \\ \\ &=& +\infty \end{array}$$

$\boxed{\lim\limits_{x\rightarrow -1^{-}}}\dfrac{g(x)-g(-1)}{x+1}=+\infty$

 

Par suite $g$ n'est pas dérivable à gauche de -1 et par conséquent $(Cg)$ admet une demi-tangente verticale en $-1^{-}$

 

$$\begin{array}{rcl} \lim\limits_{x\rightarrow -1^{+}}\dfrac{g(x)-g(-1)}{x+1}&=& \lim\limits_{x\rightarrow -1^{+}}\dfrac{g(x)}{x-1} \\ \\ &=& \lim\limits_{x\rightarrow -1^{+}}\dfrac{x}{x+1}\times\sqrt{\dfrac{-x-1}{x}} \\ \\ &=& \lim\limits_{x\rightarrow -1^{+}}-\sqrt{\left(\dfrac{x}{x+1}\right)^{2}\times\dfrac{-x-1}{x}} \\ \\ &=& \lim\limits_{x\rightarrow -1^{+}}-\sqrt{\dfrac{-x}{x+1}} \\ \\ &=& -\infty \end{array}$$

 

$\boxed{\lim\limits_{x\rightarrow -1^{+}}\dfrac{g(x)-g(-1)}{x+1}=-\infty}$

 

Par suite $g$ n'est pas dérivable à droite de $-1$ et par conséquent $(C_{g})$ admet une demi-tangente verticale en $-1^{+}$

 

Conclusion $g$ n'est pas dérivable en -1.

 

Par conséquent :

 

$(C_{g})$ admet deux demi-tangentes verticales en $-1.$

 

3) Étudier les branches infinies et la position de la courbe par rapport aux éventuelles asymptotes.

 

On a :

 

$\lim\limits_{x\rightarrow -\infty}g(x)=\lim\limits_{x\rightarrow -\infty}x\sqrt{\dfrac{x+1}{x}}=-\infty$

 

$\lim\limits_{x\rightarrow +\infty}g(x)=\lim\limits_{x\rightarrow +\infty}\dfrac{x^{3}-x^{2}}{x^{2}+1}=+\infty$

 

En $-\infty$ on a :

 

$\lim\limits_{x\rightarrow -\infty}\dfrac{g(x)}{x}=\lim\limits_{x\rightarrow -\infty}\sqrt{\dfrac{x+1}{x}}=1$

 

$\lim\limits_{x\rightarrow -\infty}[g(x)-x]=\lim\limits_{x\rightarrow -\infty}\left[x\sqrt{\dfrac{x+1}{x}}-x\right].$

 

Nous avons ici une forme indéterminée.

 

Levons l'indétermination On a :

 

$$\begin{array}{rcl} \lim\limits_{x\rightarrow -\infty}[g(x)-x] &=&\lim\limits_{x\rightarrow -\infty}\left[x\sqrt{\dfrac{x+1}{x}}-x\right] \\ \\ &=& \lim\limits_{x\rightarrow -\infty}\left[\dfrac{x^{2}(\frac{x+1}{x})-x^{2}}{x\sqrt{\frac{x+1}{x}}+x}\right]\\ \\ &=& \lim\limits_{x\rightarrow -\infty}\dfrac{1}{\sqrt{\frac{x+1}{x}}+1} \\ \\ &=&\lim\limits_{x\rightarrow -\infty}\dfrac{1}{\sqrt{1+\frac{1}{x}}+1} \\ \\ &=& \dfrac{1}{2} \end{array}$$

Par suite la droite $\boxed{(D_{1})\ :\ y=x+\dfrac{1}{2}}$ est asymptote oblique à $(Cg)$ en $-\infty$

 

En $+\infty$ on a :

 

$\lim\limits_{x\rightarrow +\infty}=\lim_{x\rightarrow +\infty}\dfrac{x^{3}-x^{2}}{x^{3}+x}=1$

$$\begin{array}{rcl} \lim\limits_{x\rightarrow +\infty}[g(x)-x] &=&\lim\limits_{x\rightarrow +\infty}\left[\dfrac{x^{3}-x^{2}}{x^{2}+1}-x\right]\\ \\ &=& \lim\limits_{x\rightarrow +\infty}\left[\dfrac{x^{3}-x^{2}-x^{3}-x}{x^{2}+1}\right] \\ \\ &=& \lim\limits_{x\rightarrow +\infty}\left[\dfrac{-x^{2}-x}{x^{2}+1}\right]\\ \\ &=& -1\end{array}$$

Par suite la droite $\boxed{(D_{2}): y=x-1}$ est asymptote oblique à $Cg$ en $+\infty$

 

Position de $Cg$ par rapport au asymptote

 

Position de $Cg$ par rapport à $(D_{1}): y=x+\dfrac{1}{2}$

 

On a en $-\infty$ :

 

$g(x)-y=x\sqrt{\dfrac{x+1}{x}}-x-\dfrac{1}{2}.$

 

Sur $]-\infty\;;\ -1]:$

 

Posons $g(x)-y\leq 0.$

 

Alors on a :

 

$\begin{array}{rcl} g(x)-y\leq 0 &\Leftrightarrow& x\sqrt{\dfrac{x+1}{x}}\leq x+\dfrac{1}{2} \\ \\ &\Leftrightarrow& \left(x\sqrt{\dfrac{x+1}{x}}\right)\geq \left(x+\dfrac{1}{2}\right)^{2}\quad \text{car les deux membres sont tous négatifs} \\ \\ &\Leftrightarrow& x^{2}\left(\dfrac{x+1}{x}\right)\geq \left(x+\dfrac{1}{2}\right)^{2} \\ \\ &\Leftrightarrow& x^{2}+x-x^{2}-\dfrac{1}{4}-x\geq 0 \\ \\ &\Leftrightarrow& -\dfrac{1}{4}\geq 0\quad \text{ce qui est impossible} \end{array}$

 

Donc $\forall\;x\ \in\;]-\infty\;;\ -1]\;,f(x)-y>0.$

 

Par conséquent :

 

sur $]-\infty\;;\ -1]$ $(Cg)$ est au dessus de $(D_{1}): y=x+\dfrac{1}{2}$

 

Sur $]-1\;;\ 0[$ :

 

Posons $g(x)-y\geq 0.$

 

Alors on a :

 

$\begin{array}{rcl} g(x)-y\geq 0 &\Leftrightarrow& x\sqrt{\dfrac{-x-1}{x}}\geq x+\dfrac{1}{2}\quad \text{avec } x\leq\dfrac{1}{2}\;\text{ car impossible si }\;x>-\dfrac{1}{2} \\ \\ &\Leftrightarrow& \left(x\sqrt{\dfrac{-x-1}{x}}\right)\leq\left(x+\dfrac{1}{2}\right)^{2}\;\text{ car les deux membres sont tous négatifs} \\ \\  &\Leftrightarrow& x^{2}\left(\dfrac{-x-1}{x}\right)\leq\left(x+\dfrac{1}{2}\right)^{2}\\ \\ &\Leftrightarrow& -x^{2}-x-x^{2}-\dfrac{1}{4}-x\leq 0 \\ \\ &\Leftrightarrow& -2x^{2}-2x-\dfrac{1}{4}\leq 0 \\ \\ &\Leftrightarrow&-8x^{2}-8x-1\leq 0 \\ \\ &\Leftrightarrow& x\in\left]-1\;;\ \dfrac{-2-\sqrt{2}}{4}\right] \end{array}$

 

Donc $\forall\;x\ \in\left]-1\;;\ \dfrac{-2-\sqrt{2}}{4}\right]\;,g(x)-y\geq 0$

 

Par conséquent :

 

sur $\left]-1\;;\ \dfrac{-2-\sqrt{2}}{4}\right]\;,\ (Cg)\;\text{est au dessus de} (D_{1}) : y=x+\dfrac{1}{2}$

 

sur $\left]\dfrac{-2-\sqrt{2}}{4}\;;\ 0\right[\;,\ (Cg)\;\text{est au dessous de}\;(D_{1}) : y=x+\dfrac{1}{2}$

 

Position de $Cg$ par rapport à $(D_{2}) : y=x-1$

 

Sur $[0\;;\ +\infty[$ : $g(x)-y=\dfrac{x^{3}-x^{2}}{x^{2}+1}-x+1$

 

Posons $g(x)-y\geq 0$

 

Alors on a :

 

$\begin{array}{rcl} g(x)-y\geq 0 &\Leftrightarrow& \dfrac{x^{3}-x^{2}}{x^{2}+1}-x+1\geq 0 \\ \\ &\Leftrightarrow& \dfrac{x^{3}-x^{2}-x^{3}+x^{2}-x+1}{x^{2}+1}\geq 0 \\ \\ &\Leftrightarrow& \dfrac{-x+1}{x^{2}+1}\geq 0 \\ \\ &\Leftrightarrow& x\;\in\ ]0\;;\ 1] \end{array}$

 

Donc $\forall\;x\in]0\;;\ 1]\;;\ g(x)-y\geq 0$

 

Par conséquent :

 

sur $]0\;;\ ]\;,(Cg)$ est au dessus de $(D_{1}) : y=x-1$

 

sur $]1\;;\ +\infty[\;,\ (Cg)$ est en dessous de $(D_{1}) : y=x-1$

 

4) Calculer $g'(x)$ sur les intervalles où $g$ est dérivable.

 

Sur $]-\infty\;;\ -1]$

 

La fonction $x\mapsto x$ est dérivable sur $\mathbb{R}$, en particulier elle l'est sur $]-\infty\;;\ -1[.$

 

La fonction $x\mapsto \sqrt{\dfrac{x+1}{x}}$ est dérivable sur $]-\infty\;;\ -1[$

 

Donc $g(x)$ est dérivable sur $]-\infty\;;\ -1[$

 

comme produit de fonctions dérivables sur $]-\infty\;;\ -1[$ et on a :

 

$\begin{array}{rcl} g'(x) &=& \sqrt{\dfrac{x+1}{x}}+x\left(\sqrt{\dfrac{x+1}{x}}\right)^{'} \\ \\ &=& \sqrt{\dfrac{x+1}{x}}+x\left(\dfrac{(\frac{x+1}{x})^{'}}{2\sqrt{\frac{x+1}{x}}}\right)\\ \\ &=& \sqrt{\dfrac{x+1}{x}}+x\left(\dfrac{\frac{x-x-1}{x^{2}}}{2\sqrt{\frac{x+1}{x}}}\right) \\ \\ &=& \sqrt{\dfrac{x+1}{x}}+x\left(\dfrac{\frac{-1}{x^{2}}}{2\sqrt{\frac{x+1}{x}}}\right) \\ \\ &=& \dfrac{2x+1}{2x\sqrt{\dfrac{x+1}{x}}} \end{array}$

 

Sur $]-1\;;\ 0[$

 

La fonction $x\mapsto x$ est dérivable sur $\mathbb{R}$, en particulier elle l'est sur $]-1\;;\ 0[.$

 

La fonction $x\mapsto \sqrt{\dfrac{-x-1}{x}}$ est dérivable sur $]-1\;;\ 0[.$

 

Donc $g(x)$ est dérivable sur $]-1\;;\ 0[$ comme produit de fonctions dérivables sur $]-1\;;\ 0[$

 

$\begin{array}{rcl} g'(x) &=& \sqrt{\dfrac{-x-1}{x}}+x\left(\sqrt{\dfrac{-x-1}{x}}\right)^{'}\\ \\ &=&\sqrt{\dfrac{-x-1}{x}}+x\left(\dfrac{(\frac{-x-1}{x})^{'}}{2\sqrt{\frac{-x-1}{x}}}\right) \\ \\ &=&\sqrt{\dfrac{-x-1}{x}}+x\left(\dfrac{\frac{-x+x+1}{x^{2}}}{2\sqrt{\dfrac{-x-1}{x}}}\right)\\ \\ &=&\sqrt{\dfrac{-x-1}{x}}+x\left(\dfrac{\frac{1}{x^{2}}}{2\sqrt{\frac{-x-1}{x}}}\right)\\ \\ &=&\dfrac{-2x-1}{2x\sqrt{\dfrac{-x-1}{x}}}\end{array}$

 

Sur $[0\;;\ +\infty[$

 

La fonction $x\mapsto\dfrac{x^{3}-x^{2}}{x^{2}+1}$ est dérivable sur $\mathbb{R}$, en particulier elle l'est sur $[0\;;\ +\infty[.$

 

Par suite $g$ est dérivable sur $[0\;;\ +\infty[$ et on a :

 

$\begin{array}{rcl} g'(x) &=& \dfrac{(3x^{2}-1)(x^{2}+1)-2x(x^{3}-x^{2})}{(x^{2}+1)^{2}}\\ \\ &=& \dfrac{3x^{4}+3x^{2}-2x^{3}-2x-2x^{4}+2x^{3}}{(x^{2}+1)^{2}} \\ \\ &=& \dfrac{x^{4}+3x^{2}-2x}{(x^{2}+1)^{2}} \end{array}$

 

Finalement on a :

 

$$g'(x)=\left\lbrace\begin{array}{lll} \dfrac{2x+1}{2x\sqrt{\frac{x+1}{x}}}& \text{si} & x\;\in\;]-\infty\;;\ -1[ \\ \\ \dfrac{-2x-1}{2x\sqrt{\frac{-x-1}{x}}} & \text{si} & x\;\in\;]-1\;;\ 0[ \\ \\ \dfrac{x^{4}+3x^{2}-2x}{(x^{2}+1)^{2}} & \text{si} & x\;\in\;[0\;;\ +\infty[ \end{array} \right.$$

5) Soit $\phi=x^{3}+3x-2$

 

a) Montrons que l'équation $\phi=0$ admet une solution unique $\alpha$ sur $\mathbb{R}$ puis donnons un encadrement de $\alpha$ par deux entiers consécutifs.

 

Montrons que l'équation $\phi(x)=0$ admet une solution unique $\alpha$ sur $\mathbb{R}$ $D\phi=\mathbb{R}$ car $\phi$ est une fonction polynômiale.

 

$\lim_{x\rightarrow -\infty}\phi(x)=-\infty$ et $\lim_{x\rightarrow +\infty}\phi(x)=+\infty$

 

$\phi$ est dérivable sur $\mathbb{R}$ (car $\phi$ est une fonction polynômiale).

 

$\forall\;x\;\in\;\mathbb{R}$ on a $\phi'(x)=3x^{2}+1>0$

 

Donc $\phi$ est strictement croissante sur $\mathbb{R}.$

 

$\phi$ étant continue et strictement croissante sur $\mathbb{R}$

 

donc elle réalise une bijection de $\mathbb{R}$ sur $\mathbb{R}.$

 

Or $0\;\in\;\mathbb{R}$ donc il existe un unique $\alpha\;\in\mathbb{R}$ tel que $\phi(\alpha)=0$

 

Donnons un encadrement de $\alpha$ par deux entiers consécutifs.

 

Comme $\phi(0)=-2$ et $\phi(1)=2$ donc $\phi(0)\times\phi(1)<0.$

 

Par suite $0<\alpha<1$

 

b) En déduire le signe de $\phi$ sur $\mathbb{R}.$

 

On a :

 

$\forall\;x\ \in\;]-\infty\;;\ \alpha]\;,\ \phi(x)\leq 0$

 

$\forall\;x\in\;]\alpha\;;\ +\infty[\;,\ \phi(x)>0$

 

6) Montrons que $g'(x)=\dfrac{x\phi(x)}{(x^{2}+1)^{2}} sur [0\;;\ +\infty[$ puis établir le tableau de variation de $g$ sur $\mathbb{R}$

 

On a :

 

$\forall\;x\ \in\;[0\;;\ +\infty[\;,\;g'(x)=\dfrac{x^{4}+3x^{2}-2x}{(x^{2}+1)^{2}}=\dfrac{x(x^{3}+3x-2)}{(x^{2}+1)^{2}}=\dfrac{x\phi(x)}{(x^{2}+1)^{2}}$

 

Tableau de variations de $g.$

 

Sur $[0\;;\ +\infty[$

 

Le signe de $\phi(x)$ dépend de celui de $x\phi(x).$

 

$\forall\;x\ \in\;]\alpha\;;\ +\infty[\;,\ \phi(x)\leq 0$

 

donc $x\phi(x)>0$ ou encore $g'(x)\leq 0$

 

D'où $g$ est strictement croissante sur $]\alpha\;;\ +\infty[$

 

$\forall\;x\ \in\;]0\;;\ \alpha]\;,\ \phi(x)\leq 0$ donc $x\phi(x)\leq 0$ ou encore $g'(x)\leq 0$

 

D'où $g$ est décroissante sur $]\alpha\;;\ +\infty[$

 

Sur $]-\infty\;;\ -1[$

 

on a $g'(x)=\dfrac{2x+1}{2x\sqrt{\frac{x+1}{x}}}$

 

Sur $\left]\alpha\;;\ -\dfrac{1}{2}\right]\;,\ g'(x)\geq 0$ donc $\forall\;x\;\in\;]-\infty\;;\ -1[\;g'(x)\geq 0$

 

D'où $g$ est croissante sur $]-\infty\;;\ -1[.$

 

Sur $]-1\;;\ 0[$

 

on a $g'(x)=\dfrac{-2x-1}{2x\sqrt{\dfrac{-x-1}{x}}}.$

 

Sur $\left]-1\;;\ -\dfrac{1}{2}\right]\;,\;g'(x)\leq 0$ donc $\forall\;x\;\in\;\left]-1\;;\ -\dfrac{1}{2}\right[\;,\ g'(x)\leq 0$

 

D'où $g$ est décroissante sur $\left]-1\;;\ -\dfrac{1}{2}\right]$

 

Sur $\left]-\dfrac{1}{2}\;;\ 0\right]\;,\ g'(x)>0$ donc $\forall\;x\ \;\left]-\dfrac{1}{2}\;;\ 0\right[\;,\ g'(x)\leq 0$

 

D'où $g$ est croissante sur $\left]-\dfrac{1}{2}\;;\ 0\right[.$

 

$$\begin{array}{|c|lcr|lcr|lcr|lcr|lcr|} \hline x&-\infty&    &-1&   & &-\dfrac{1}{2}&     & &0&     & &\alpha&     &   &+\infty \\ \hline g'(x) &   &+&   &   &-&   &   &+&   &   &-&   &   &+&   \\ \hline  &   & &   &   & &   &   & &   &   & &   &   & &   \\  g &   &\nearrow&   &   &\searrow&   &   &\nearrow&    &   &\searrow&   &    &\nearrow&  \\  &   & &   &   & &   &   & &   &   & &   &   & &   \\ \hline \end{array}$$

 

Les maximums (locaux) de $g$ sont $A(-1\;;\ 0)$ et $O(0\;;\ 0)$

 

Les minimums (locaux) de $g$ sont $C\left(-\dfrac{1}{2}\;;\ -\dfrac{1}{2}\right)\ $ et $\ D(\alpha\;;\ g(\alpha)) $

 

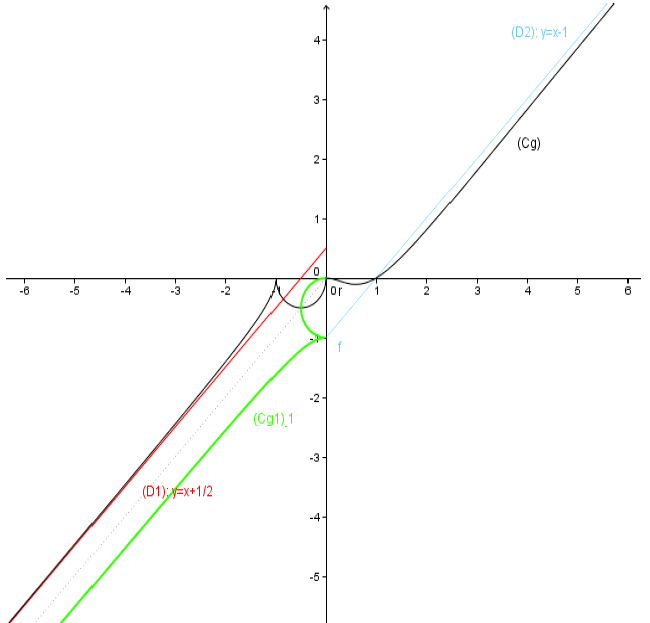
7) Traçons les droites remarquables puis tracer $Cg$ la courbe de $g.$

 

Asymptote oblique en $-\infty$ : $(D_{1}): y=x+\dfrac{1}{2}$

 

Asymptote oblique en $+\infty$ :$(D_{2}) : y=x-1$

 

 

a) Montrons que la restriction $g_{1}$ de $g$ à $]-\infty\;;\ -1]$ est bijective de $]-\infty\;;\ -1]$ sur un intervalle $J$ à préciser.

 

$g_{1}(x)=x\sqrt{\dfrac{x+1}{x}}$

 

D'après le tableau de variation, $g_{1}$ est continue et croissante sur $]-\infty\;;\ -1]$

 

donc elle réalise une bijection de $]-\infty\;;\ -1]$ sur $J=g_{1}(]-\infty\;;\ -1])=]-\infty\;;\ 0]$

 

b) $g_{1}^{-1}$ la bijection réciproque de $g_{1}$, est-elle dérivable sur $J$ ?

 

Calculer $g_{1}(-2)$ puis $(g_{1}^{-1})'(-\sqrt{2})$

 

Comme $g_{1}$ est dérivable et $g'_{1}(x)\neq 0$ sur $]-\infty\;;\ -1[$ donc $g_{1}^{-1}$ est dérivable sur $]-\infty\;;\ 0[$

 

on a $g_{1}(-2)=-2\sqrt{\dfrac{-2+1}{-2}}=-\dfrac{2}{\sqrt{2}}=-\sqrt{2}$

 

$(g_{1}^{-1})'(-\sqrt{2})=\dfrac{1}{g'_{1}(-\sqrt{2})}=\dfrac{-2\sqrt{2}}{3}$

 

c) Donnons les variations de $g_{1}^{-1}$

 

$g_{1}$ et $g_{1}^{-1}$ ont même sens de variation.

 

Puisque $g_{1}$ est croissante sur $]-\infty\;;\ -1]$ donc $g_{1}^{-1}$ est aussi croissante sur $]-\infty\;;\ 0]$

 

Traçons $Cg_{1}^{-1}.$ 

 

$Cg_{1}^{-1}$ se déduit de $Cg_{1}$ par la symétrie d'axe la première bissectrice (la droite $y=x$) (voir figure)