Corrigé devoir n° 5 maths - 4e
Classe:
Quatrième
Exercice 1
1) Effectuons les opérations suivantes :
Soit : $A=\dfrac{2}{3}+\left[\dfrac{5}{3}\times\left(1-\dfrac{1}{2}\right)-\dfrac{2}{6}\right]$
Alors,
$\begin{array}{rcl} A&=&\dfrac{2}{3}+\left[\dfrac{5}{3}\times\left(\dfrac{2}{2}-\dfrac{1}{2}\right)-\dfrac{2}{6}\right]\\\\&=&\dfrac{2}{3}+\left[\dfrac{5}{3}\times\left(\dfrac{1}{2}\right)-\dfrac{2}{6}\right]\\\\&=&\dfrac{2}{3}+\left[\dfrac{5}{6}-\dfrac{2}{6}\right]\\\\&=&\dfrac{2}{3}+\dfrac{3}{6}\\\\&=&\dfrac{4}{6}+\dfrac{3}{6}\\\\&=&\dfrac{7}{6}\end{array}$
Donc, $\boxed{A=\dfrac{7}{6}}$
Soit : $B=\dfrac{1}{4}-\dfrac{1}{2}\times\dfrac{2}{5}+\dfrac{2}{3}$
Alors,
$\begin{array}{rcl} B&=&\dfrac{1}{4}-\dfrac{1}{2}\times\dfrac{2}{5}+\dfrac{2}{3}\\\\&=&\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{2}{3}\\\\&=&\dfrac{15}{60}-\dfrac{12}{60}+\dfrac{40}{60}\\\\&=&\dfrac{15-12+40}{60}\\\\&=&\dfrac{43}{60}\end{array}$
D'où, $\boxed{B=\dfrac{43}{60}}$
Soit : $C=4-\dfrac{7}{10}+\dfrac{1}{3}-\dfrac{1}{6}-\dfrac{7}{3}$
Alors,
$\begin{array}{rcl} C&=&4-\dfrac{7}{10}+\dfrac{1}{3}-\dfrac{1}{6}-\dfrac{7}{3}\\\\&=&4-\dfrac{7}{10}+\dfrac{1}{3}-\dfrac{7}{3}-\dfrac{1}{6}\\\\&=&4-\dfrac{7}{10}-\dfrac{6}{3}-\dfrac{1}{6}\\\\&=&\dfrac{120}{30}-\dfrac{21}{30}-\dfrac{60}{30}-\dfrac{5}{30}\\\\&=&\dfrac{120-21-60-5}{30}\\\\&=&\dfrac{34}{30}\\\\&=&\dfrac{17}{15}\end{array}$
Ainsi, $\boxed{C=\dfrac{17}{15}}$
Soit : $D=\dfrac{\dfrac{\dfrac{1}{4}}{5}-\dfrac{1}{3}}{\dfrac{1}{7}-\dfrac{3}{\dfrac{5}{2}+4}}$
Alors,
$\begin{array}{rcl} D&=&\dfrac{\dfrac{\dfrac{1}{4}}{5}-\dfrac{1}{3}}{\dfrac{1}{7}-\dfrac{3}{\dfrac{5}{2}+4}}\\\\&=&\dfrac{\dfrac{1}{4}\times\dfrac{1}{5}-\dfrac{1}{3}}{\dfrac{1}{7}-\dfrac{3}{\dfrac{5}{2}+\dfrac{8}{2}}}\\\\&=&\dfrac{\dfrac{1}{20}-\dfrac{1}{3}}{\dfrac{1}{7}-\dfrac{3}{\dfrac{13}{2}}}\\\\&=&\dfrac{\dfrac{3}{60}-\dfrac{20}{60}}{\dfrac{1}{7}-\dfrac{3}{1}\times\dfrac{2}{13}}\\\\&=&\dfrac{-\dfrac{17}{60}}{\dfrac{1}{7}-\dfrac{6}{13}}\\\\&=&\dfrac{-\dfrac{17}{60}}{\dfrac{13}{91}-\dfrac{42}{91}}\\\\&=&\dfrac{-\dfrac{17}{60}}{-\dfrac{29}{91}}\\\\&=&\left(-\dfrac{17}{60}\right)\times\left(-\dfrac{91}{29}\right)\\\\&=&\dfrac{1547}{1740}\end{array}$
D'où, $\boxed{D=\dfrac{1547}{1740}}$
2) Écrivons le plus simple possible les expressions suivantes :
$\begin{array}{rcl} E&=&\dfrac{\left(2^{-1}\right)^{3}\times 3^{2}}{\left(2^{2}\times3\right)^{3}\times\left(3^{2}\right)^{2}}\\\\&=&\dfrac{2^{(-1)\times 3}\times 3^{2}}{2^{2\times 3}\times 3^{3}\times 3^{2\times 2}}\\\\&=&\dfrac{2^{-3}\times 3^{2}}{2^{6}\times 3^{3}\times 3^{4}}\\\\&=&2^{-3}\times 3^{2}\times 2^{-6}\times 3^{-3}\times 3^{-4}\\\\&=&2^{-3}\times 2^{-6}\times 3^{2}\times 3^{-3}\times 3^{-4}\\\\&=&2^{-3-6}\times 3^{2-3-4}\\\\&=&2^{-9}\times 3^{-5}\end{array}$
Donc, $\boxed{E=2^{-9}\times 3^{-5}}$
$\begin{array}{rcl} F&=&\dfrac{a^{4}\times b^{3}\times c^{2}}{a^{5}\times b^{4}\times c^{3}}\\\\&=&a^{4}\times b^{3}\times c^{2}\times a^{-5}\times b^{-4}\times c^{-3}\\\\&=&a^{4}\times a^{-5}\times b^{3}\times b^{-4}\times c^{2}\times c^{-3}\\\\&=&a^{4-5}\times b^{3-4}\times c^{2-3}\\\\&=&a^{-1}\times b^{-1}\times c^{-1}\\\\&=&(a\times b\times c)^{-1}\\\\&=&\dfrac{1}{a\times b\times c}\end{array}$
D'où, $\boxed{F=(a\times b\times c)^{-1}=\dfrac{1}{a\times b\times c}}$
3) Donnons l'écriture scientifique des expressions suivantes :
On a :
$\begin{array}{rcl} G&=&40^{2}\\\\&=&1\,600\\\\&=&1.6\times 1\,000\\\\&=&1.6\times 10^{3}\end{array}$
Donc, $\boxed{G=1.6\times 10^{3}}$
Soit :
$\begin{array}{rcl} H&=&\dfrac{2\times 10^{-2}\times 3\times10^{-3}}{3\times 10^{4}\times 0.0001}\\\\&=&\dfrac{2\times 3\times 10^{-2}\times 10^{-3}}{3\times 10^{4}\times 10^{-4}}\\\\&=&\dfrac{2\times 10^{-2-3}}{10^{4-4}}\\\\&=&\dfrac{2\times 10^{-5}}{10^{0}}\\\\&=&\dfrac{2\times 10^{-5}}{1}\\\\&=&2\times 10^{-5}\end{array}$
D'où, $\boxed{H=2\times 10^{-5}}$
4) Donner un encadrement de $\dfrac{22}{7}$ à $10^{-3}$ près.
On a : $\dfrac{22}{7}=3.142857...$
Alors, un encadrement de $\dfrac{22}{7}$ à $10^{-3}$ près est donné par :
$$3.142<\dfrac{22}{7}<3.143$$
a) Donnons l'approximation décimale par défaut et par excès de $\dfrac{22}{7}$
Comme $3.142<\dfrac{22}{7}<3.143$ alors :
$-\ $ l'approximation décimale par défaut de $\dfrac{22}{7}$ est égale à $3.142$
$-\ $ l'approximation décimale par excès de $\dfrac{22}{7}$ est égale à $3.143$
b) Arrondissons au dixième et au centième près $\dfrac{22}{7}.$
au dixième près, $\dfrac{22}{7}$ est égale à $3.1$
au centième près, $\dfrac{22}{7}$ est égale à $3.14$
Exercice 2
$C_{1}$ est un cercle de centre $O_{1}$ et de rayon $R_{1}$, $C_{2}$ est un cercle de centre $O_{2}$ et de rayon $R_{2}.$
Complétons le tableau ci-dessous.
$$\begin{array}{|c|c|c|c|c|c|}\hline R_{1}&5&5&6&10&10\\\hline R_{2}&3&6&9&7&5\\\hline O_{1}O_{2}&5&1&15&2&20\\\hline R_{1}+R_{2}&8&11&15&17&15\\\hline|R_{1}-R_{2}|&2&1&3&3&5\\\hline\text {Positions relatives}&\text{sécants}&\text{tangents}&\text{tangents}&\text{disjoints}&\text{disjoints}\\\text {de } C_{1} \text { et } C_{2}&&\text{intérieurement}&\text{extérieurement}&\text{intérieurement}&\text{extérieurement}\\\hline\end{array}$$
Exercice 3
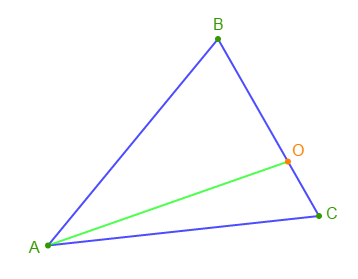
$ABC$ est un triangle et $O$ un point de $[BC]$

1.a) Démontrons que :
$$BC=BO+OC\;;\quad OA<AB+OB\;;\quad OA<AC+OC$$
Comme $O\in[BC]$ alors, $BC=BO+OC$
Par ailleurs, $ABC$ étant un triangle et $O$ un point de $[BC]$ alors, $ABO\ $ et $\ ACO$ sont des triangles.
Ainsi, en utilisant l'inégalité triangulaire, on a :
$B\notin[OA]$ donc, $OA<AB+OB$
$C\notin[OA]$ donc, $OA<AC+OC$
b) En déduisons que $OA<\dfrac{1}{2}(AB+BC+AC)$
On a :
$$\begin{array}{rcl} OA&<&AB+OB\\\\ OA&<&AC+OC\end{array}$$
Alors, en additionnant membre à membre ces deux inégalités, on obtient :
$$OA+OA<AB+OB+AC+OC$$
Ce qui donne,
$$2OA<AB+OB+OC+AC$$
Or, on sait que : $OB+OC=BC$
Donc, en remplaçant $OB+OC$ par $BC$, on obtient :
$$2OA<AB+BC+AC$$
D'où,
$$OA<\dfrac{1}{2}(AB+BC+AC)$$
Exercice 4
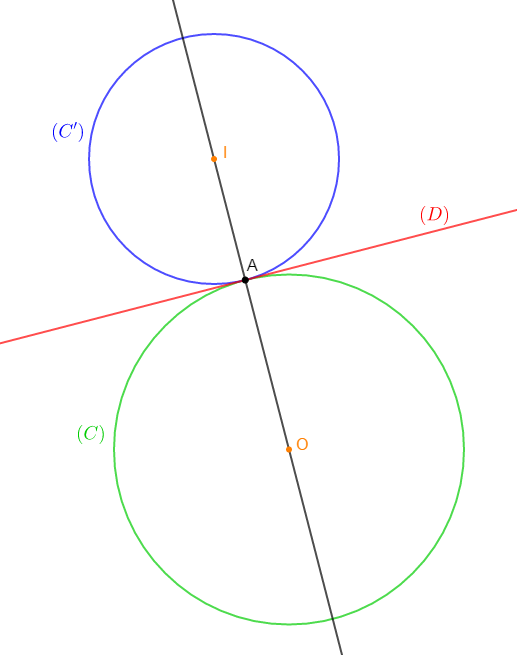
Soit $(C)$ un cercle de centre $O$ et de rayon $r=3.5\;cm$ et un point $A$ sur le cercle
1) Traçons la droite $D$ perpendiculaire à la droite $(OA)$ en $A.$
Justifions que la droite $(D)$ est tangente en $A$ à $(C).$
On constate que la droite $(D)$ touche le cercle $(C)$ au point $A$ et perpendiculairement au rayon $[OA].$
Par conséquent, la droite $(D)$ est tangente en $A$ à $(C).$
2) Plaçons le point $I$ sur la demi-droite $[OA)$ tel que $OI=6\;cm$ puis tracer le cercle $(C')$ de centre $I$ et de rayon $r'=2.5\;cm$
3) Montrons que les cercles $(C)\ $ et $\ (C')$ sont tangents.
On a : $OI=6\;cm\ $ et $\ r+r'=3.5+2.5=6\;cm$
Ainsi, on constate que : $OI=r+r'$
Ce qui montre que les cercles $(C)\ $ et $\ (C')$ sont tangents extérieurement.

Auteur:
Diny Faye

Commentaires
Moouhamadou Lam... (non vérifié)
jeu, 11/23/2023 - 22:28
Permalien
Jejizifzkeijd
Ju (non vérifié)
mer, 11/27/2024 - 20:43
Permalien
Vous avez commis une erreur à
Ajouter un commentaire