Corrigé Bac Maths S2 1er groupe 2011
Classe:
Terminale
Exercice 1
I. 1) $Z$ est écrit sous forme algébrique, $X$ est sa partie réelle et $y$ sa partie imaginaire (ou $\mathrm{i}y).$
2) Son module est $|Z|=\sqrt{x^{2}+y^{2}}.$
3) $\cos\alpha=\dfrac{\Re e(Z)}{|Z|}\:,\quad\sin\alpha=\dfrac{\Im m(Z)}{|Z|}$
4) Soit $O(0)\;,\ Z’- Z_{O}=\mathrm{e}^{\mathrm{i}\theta}\left(Z-Z_{O}\right)$
$$\boxed{Z'=Z\mathrm{e}^{\mathrm{i}\theta}}$$
II. $(E) : \dfrac{1}{2}Z^{2}+4Z\sqrt{3}+32=0$
1)
$\begin{array}{rcl} \Delta'&=&(2\sqrt{3})^{2}-16\\ \\&=&-4\\ \\&=&(2\mathrm{i})^{2}\end{array}$
Donc, $\Delta'=(2\mathrm{i})^{2}$
Par suite, $Z_{1}=\dfrac{-2\sqrt{3}-2\mathrm{i}}{\dfrac{1}{2}}\ $ et $\ Z_{2}=\dfrac{-2\sqrt{3}+2\mathrm{i}}{\dfrac{1}{2}}$
On obtient : $\boxed{Z_{1}=-4\sqrt{3}-4\mathrm{i}}\ $ et $\ \boxed{Z_{2}=-4\sqrt{3}+4\mathrm{i}} $
2) $a=-4\sqrt{3}-4\mathrm{i}\;,\ b=-4\sqrt{3}+4\mathrm{i}$
On a : $OA=|a|=8\;,\ OB=|b|=8\ $ et $\ AB=|8\mathrm{i}|=8.$ Donc $OAB$ est un triangle équilatéral.
3)
$\begin{array}{rcl} Z_{D}&=&Z_{C}\mathrm{e}^{\mathrm{i}\tfrac{\pi}{3}}\\ \\&=&\left(\dfrac{1}{2}+\mathrm{i}\dfrac{\sqrt{3}}{2}\right)\left(\sqrt{3}+\mathrm{i}\right)\\ \\&=&\dfrac{1}{2}\mathrm{i}(\sqrt{3}-\mathrm{i})(\sqrt{3}+\mathrm{i})\\ \\&=&\dfrac{1}{2}\mathrm{i}\times 4\end{array}$
$$\boxed{Z_{D}=2\mathrm{i}}$$
4) $G$ = barycentre du système $\{(O\;,\ 1)\;,\ (D\;,\ -1)\;,\ (B\;,\ -1)\}.$
a)
$\begin{array}{rcl} g&=&\dfrac{1.Z_{0}-1.Z_{D}-1.Z_{B}}{-1}\\ \\&=&Z_{D}+Z_{B}\\ \\&=&2\mathrm{i}+(-4\sqrt{3}+4\mathrm{i})\\ \\&=&-4\sqrt{3}+6\mathrm{i}\end{array}$
$$\boxed{g=-4\sqrt{3}+6\mathrm{i}}$$
b) Plaçons les points $A\;,\ B\;,\ C\ $ et $\ G$ dans le repère $(O\;,\ \vec{u}\;,\ \vec{v})$
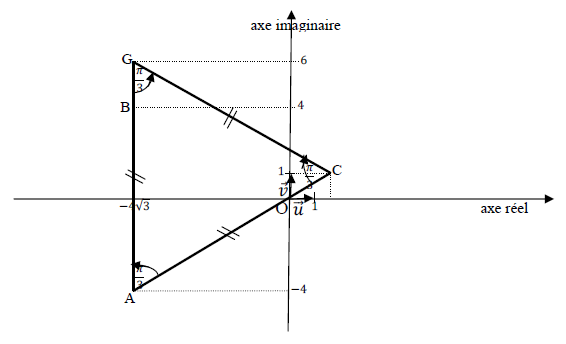
On vérifie que : $\dfrac{c-g}{a-g}=\dfrac{1}{2}+\mathrm{i}\dfrac{\sqrt{3}}{2}$
Donc, $\left\lbrace\begin{array}{rcl} |c-g|&=&|a-g|\\ \\arg\left(\dfrac{c-g}{a-g}\right)&=&\dfrac{\pi}{3}\;[2\pi]\end{array}\right.$
D'où :
$$\left\lbrace\begin{array}{rcl} GA&=&GC\\ \\(\overrightarrow{GA}\;,\ \overrightarrow{GC})&=&\dfrac{\pi}{3}\; [2\pi]\end{array}\right.$$
Donc, $GAC$ est un triangle équilatéral direct.
Exercice 2
I. $p(A)=\dfrac{Card\;A}{Card\;\Omega}\;,\quad p(A/B)=\dfrac{Card\;(A\cap B)}{Card\;B}$
$p(A)=p(A\cap\overline{B})+p(A\cap B)$, car $A=(A\cap\overline{B})\cup(A\cap B)\ $ et $\ A\cap\overline{B}\ $ et $\ A\cap B$ sont deux événements incompatibles.
II. 1) $p(D_{1})=1\;,\quad p(D_{n+1}/D_{n})=\dfrac{2}{9}\;,\quad p(D_{n+1}/\overline{D}_{n})=\dfrac{5}{6}$
2) $p(D_{n+1})=p_{n+1}$
$p(D_{n+1})=p(D_{n+1}\cap D_{n})+p(D_{n+1}\cap\overline{D}_{n})\ $ or, $p(D_{n+1})=p_{n+1}$
Donc, $p_{n+1}=p(D_{n})p(D_{n+1}/D_{n})+p(\overline{D}_{n})p(D_{n+1}/\overline{D}_{n})$
D'où, $p_{n+1}=\dfrac{2}{9}p_{n}+(1-p_{n})\dfrac{5}{6}$
Ainsi,
$$\boxed{p_{n+1}=-\dfrac{11}{18}p_{n}+\dfrac{5}{6}}$$
3) $U_{n}=6p_{n}-\dfrac{90}{29}\;;\ n\in\mathbb{N}^{*}$
a)
$\begin{array}{rcl} U_{n}&=&6p_{n}-\dfrac{90}{29}\\ \\&=&6\left(p_{n}-\dfrac{15}{29}\right)\end{array}$
Donc, $U_{n+1}=6\left(p_{n+1}-\dfrac{15}{29}\right)$
En remplaçant $p_{n+1}$ par son expression, on a :
$\begin{array}{rcl} U_{n+1}&=&6\left(-\dfrac{11}{18}p_{n}+\dfrac{5}{6}-\dfrac{15}{29}\right)\\ \\&=&6\left(-\dfrac{11}{18}p_{n}+\dfrac{55}{6\times 29}\right)\\ \\&=&6\times\dfrac{-11}{18}\left(p_{n}-\dfrac{55}{11}\times\dfrac{18}{6\times 29}\right)\\ \\&=&-\dfrac{11}{18}\left(6p_{n}-\dfrac{90}{29}\right)\end{array}$
Donc, $\boxed{q=-\dfrac{11}{18}}$
b) $U_{n}=U_{1}\times q^{n-1}$
$\begin{array}{rcl} U_{1}&=&6p_{1}-\dfrac{90}{29}\\ \\&=&6-\dfrac{90}{29}\\ \\&=&\dfrac{84}{29}\end{array}$
Donc, $\boxed{U_{1}=\dfrac{84}{29}}$
D'où :
$$\boxed{U_{n}=\dfrac{84}{29}\times\left(\dfrac{-11}{18}\right)^{n-1}\;;\ n\in\mathbb{N}^{*}}$$
$p_{n}=\dfrac{1}{6}\left(U_{n}+\dfrac{90}{29}\right)$
Par suite,
$$\boxed{p_{n}=\dfrac{1}{6}\left[\dfrac{84}{29}\times\left(\dfrac{-11}{18}\right)^{n-1}+\dfrac{90}{29}\right]}$$
c) Soit $q_{20}$ la probabilité que la ville soit sans délestage le $20^{eme}$ jour.
Alors, $q_{20}=1-p_{20}$
Ainsi, $\boxed{q_{20}\cong 6.483}$ à $10^{-3}$ prés par défaut.
Problème
I. $f(x)=\dfrac{3(x-1)^{3}}{3x^{2}+1}$
Soit $D_{f}$ le domaine de définition de la fonction $f\;,$
$D_{f}=\mathbb{R}\ $ car $\ 3x^{2}+1\neq 0$ pour tout $x\in\mathbb{R}$
1)
$$\lim_{x\rightarrow -\infty}f(x)=-\infty\qquad\lim_{x\rightarrow +\infty}f(x)=+\infty$$
2) $x\mapsto(x-1)^{3}$ est dérivable sur $\mathbb{R}$ comme puissance d'une fonction dérivable sur $\mathbb{R}.$
D'où par produit $x\mapsto 3(x-1)^{3}$ est dérivable sur $\mathbb{R}$
$x\mapsto 3x^{2}+1$ dérivable sur $\mathbb{R}$ et $3x^{2}+1\neq 0$ pour tout réel ; par quotient $x\mapsto f(x)$ dérivable sur $\mathbb{R}.$
Calculons $f'(x)$
$\begin{array}{rcl} f'(x)&=&3\dfrac{3(x-1)^{2}(3x^{2}+1)-(x-1)^{3}(6x)}{(3x^{2}+1)^{2}}\\ \\&=&3(x-1)^{2}\left[\dfrac{3(3x^{2}+1)-(x-1)(6x)}{(3x^{2}+1)^{2}}\right]\\ \\&=&3(x-1)^{2}\left[\dfrac{9x^{2}+3-6x^{2}+6x}{(3x^{2}+1)^{2}}\right]\\ \\&=&\dfrac{9(x-1)^{2}(x+1)^{2}}{(3x^{2}+1)^{2}}\end{array}$
Ainsi, $$\boxed{f'(x)=\dfrac{9(x-1)^{2}(x+1)^{2}}{(3x^{2}+1)^{2}}}$$
Pour tout réel $x\;;\ f'(x)\geq 0$
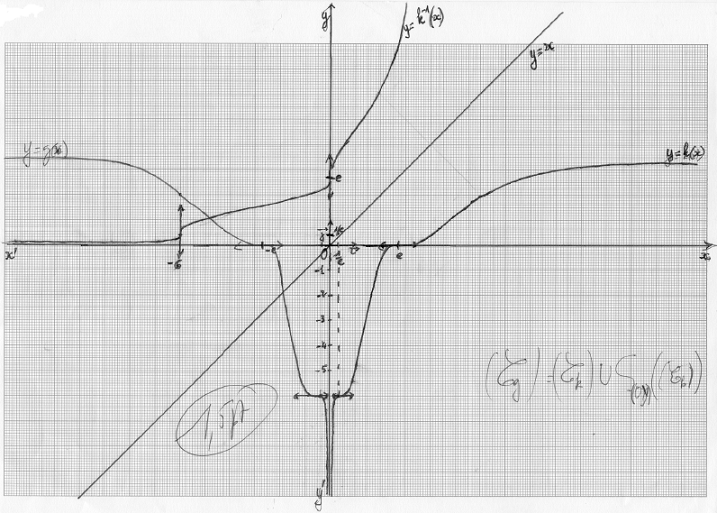
Tableau de variation de $f$
$$\begin{array}{|c|lcccccr|}\hline x&-\infty&&-1&&1&&+\infty\\ \hline f'(x)&&+&0&+&0&+&\\ \hline&&&&&&&+\infty\\&&&\vdots&&\vdots&\nearrow&\\f&&&\vdots&&0&&\\&&&\vdots&\nearrow&\vdots&&\\&&&-6&&\vdots&&\\&&\nearrow&\vdots&&\vdots&&\\&-\infty&&&&&&\\ \hline\end{array}$$
3) $f$ continue et strictement croissante sur $\mathbb{R}$ donc $f$ réalise une bijection continue de $\mathbb{R}$ sur $f(\mathbb{R})=\mathbb{R}$ et $1\in\;f(\mathbb{R}).$
Donc, d'après le corollaire du théorème des valeurs intermédiaires l'équation $f(x)=1$ admet une
solution unique $\alpha\in\mathbb{R}$
Montrons $3<\alpha<4.$
La restriction de $f$ à $[3\;;\ 4]$ est une bijection continue et $f(3)<1<f(4)$ donc, l'équation $f(x)=1$ admet une solution $\alpha\in]3\;;\ 4[.$
II. $g(x)=\dfrac{3(\ln|x|-1)^{3}}{3\ln^{2}|x|+1}$
1) a) $g(x)$ existe si, et seulement, $\left\lbrace\begin{array}{rcl} x&\neq&0\\3\ln^{2}|x|+1&\neq&0\end{array}\right.$
Or, $3\ln^{2}|x|+1\neq 0$ pour tout réel $x\neq 0$
D'où :
$$\boxed{D_{g}=\mathbb{R}^{*}}$$
b) $g(x)=\dfrac{3(\ln|x|-1)^{3}}{3(\ln|x|)^{2}+1}$
$g(x)=f(\ln|x|)$ en posant $h(x)=\ln|x|$, on a :
$$\boxed{g(x)=(f\circ h)(x)\;;\ x\neq 0}$$
c) $D_{g}=\mathbb{R}^{*}$
Soit $x\in D_{g}$ donc $-x \in D_{g}$ (car $\mathbb{R}^{*}$ stable par passage à l'opposé)
$g(-x)=f(h(-x))$ or $h$ est paire $\Rightarrow h(-x)=x$
D'où :
$$\boxed{g(-x)=g(x),\;x\neq 0}$$
$$\boxed{g(-x)=g(x),\;x\neq 0}$$
Ainsi, $g$ est paire sur $D_{g}.$
d) $D_{E}=]0\;,\ +\infty[$
$x>0$ donc, $h(x)=\ln x\ $ or $\ k(x)=f(h(x))$
$$\lim_{x\rightarrow 0^{+}}h(x)=-\infty\quad\text{et}\quad\lim_{x\rightarrow -\infty}f(x)=-\infty$$
Par composée, on obtient :
$$\boxed{\lim_{x\rightarrow 0^{+}}k(x)=-\infty}$$
$$\lim_{x\rightarrow +\infty}h(x)=+\infty\quad\text{et}\quad\lim_{x\rightarrow +\infty}f(x)=+\infty$$
Par composée, on obtient :
$$\boxed {\lim_{x\rightarrow +\infty}k(x)=+\infty}$$
Étude des branches infinies en $+\infty$
Soit $k(x)=\dfrac{3(\ln x-1)^{3}}{3\ln^{2}x+1}$ alors :
$\begin{array}{rcl}\text{Pour } x>0\;;\ \dfrac{k(x)}{x}&=&\dfrac{3(\ln^{3}x-3\ln x^{2}+3\ln x-1)}{x(3\ln^{2}x+1)}\\ \\&=&\dfrac{3\ln x}{x}\dfrac{\left[1-\dfrac{3}{\ln x}+\dfrac{3}{\ln x^{2}}-\dfrac{1}{\ln x^{3}}\right]}{\left[3+\dfrac{1}{\ln^{2}x}\right]}\end{array}$
Ainsi,
$$\lim_{x\rightarrow +\infty}\dfrac{k(x)}{x}=0$$
D'où, $(\mathcal{C}_{k})$ admet en $+\infty$ une branche parabolique de direction celle de l'axe des abscisses.
2)a) On a : $k(x)=(f\circ h)(x)$
En utilisant la forme de la dérivation d'une forme composée on obtient :
$\begin{array}{rcl} k'(x)&=&h'(x)\times f'(h(x))\\ \\&=&\dfrac{1}{x}f'(h(x))\end{array}$
Donc, $\boxed{k'(x)=\dfrac{1}{x}f'(h(x))}$
$k'(x)$ garde un signe positif sur $]0\;,\ +\infty[$ mais $k’(x)$ s'annule en $x$ vérifiant $\ln x-1=0\ $ ou $\ \ln x+1=0$
c'est à dire ; $x=\mathrm{e}\ $ ou $\ x=\dfrac{1}{\mathrm{e}}$
Tableau de variation de $k$
$$\begin{array}{|c|lcccccr|}\hline x&0&&1/\mathrm{e}&&\mathrm{e}&&+\infty\\ \hline k'(x)&|&+&0&+&0&+&\\ \hline&|&&&&&&+\infty\\&|&&\vdots&&\vdots&\nearrow&\\k&|&&\vdots&&0&&\\&|&&\vdots&\nearrow&\vdots&&\\&|&&-6&&\vdots&&\\&|&\nearrow&\vdots&&\vdots&&\\&-\infty&&&&&&\\ \hline\end{array}$$
$k\left(\dfrac{1}{\mathrm{e}}\right)=\dfrac{3(-1-1)^{3}}{3+1}=-6$
b)
$\begin{array}{rcrcl} k(x)=0&\Leftrightarrow&3(\ln x-1)^{3}&=&0\\ \\&\Leftrightarrow&\ln x-1&=&0\\ \\&\Leftrightarrow&\ln x&=&1\\ \\&\Leftrightarrow&x&=&\mathrm{e}\end{array}$
$(\mathcal{C}_{k})$ coupe l'axe des abscisses en $A(\mathrm{e}\;,\ 0)$
$\boxed{\begin{array}{l}\text{Si}\quad x\in\; ]0\;,\ \mathrm{e}[\;,\ k(x)<0\\ \\ \text{Si}\quad x\in\; ]\mathrm{e}\;,\ +\infty\;,\ k(x)>0\\ \\ \text{Si}\quad x=\mathrm{e}\;,\ k(x)=0\end{array}}$
3) a) $k$ est continue et strictement croissante sur $]0\;,\ +\infty[$ par composée de deux fonctions continue et strictement croissante. D'où, $k$ réalise une bijection de $]0\;,\ +\infty[$ sur $\mathbb{R}.$
Par suite, $k(]0\;;\ +\infty[)=\mathbb{R}$
Ainsi, $J=\mathbb{R}$


Commentaires
Anonyme (non vérifié)
lun, 05/31/2021 - 23:03
Permalien
Stdtdtr
Ajouter un commentaire