Calcul Vectoriel - 2nd
Classe:
Seconde
I. Addition vectorielle
Activité
Soient $A$ un point, $\vec{u}\ $ et $\ \vec{v}$ deux vecteurs du plan.
1) Construire $B\ $ et $\ C$ tels que $\vec{u}=\overrightarrow{AB}\ $ et $\ \vec{v}=\overrightarrow{AC}.$
2) Construire le point $D$ tel que $[BC]\ $ et $\ [AD]$ aient même milieu.
3) a) Montrer que $\overrightarrow{AC}=\overrightarrow{BD}$
b) En déduire que $\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AD}.$
Résolution
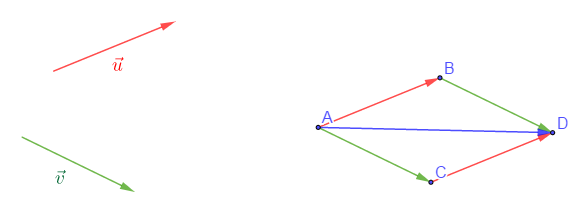
3) a) $ABDC$ est un parallélogramme donc, $\overrightarrow{AC}=\overrightarrow{BD}$
b) Comme $\overrightarrow{AC}=\overrightarrow{BD}$ alors on a : $\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BD}=\overrightarrow{AD}$
I.1 Définitions
$A$ un point du plan , $\vec{u}\ $ et $\ \vec{v}$ deux vecteurs.
$B$ et $C$ les points tels que $\vec{u}=\overrightarrow{AB}\ $ et $\ \vec{v}=\overrightarrow{AC}.$
Soit $D$ le point du plan tel que $[BC]\ $ et $\ [AD]$ aient même milieu.
On appelle vecteur somme de $\vec{u}\ $ et $\ \vec{v}$ le vecteur $\vec{w}=\overrightarrow{AD}$ et on a : $$\vec{w}=\vec{u}+\vec{v}$$
Remarques :
$\centerdot\ \ \overrightarrow{AB}=\vec{u}$, on dira que le point $B$ est l'image du point $A$ par la translation du vecteur $\vec{u}$ qui est notée
$$t_{\vec{u}}\;;\quad t_{\vec{u}}(A)=B$$
$\centerdot\ \ \overrightarrow{AC}=\vec{v}$, on dira que le point $C$ est l'image du point $A$ par la translation du vecteur $\vec{v}$ qui est notée
$$t_{\vec{v}}\;;\quad t_{\vec{v}}(A)=C$$
$$t_{\vec{u}}\;;\quad t_{\vec{u}}(A)=B$$
$\centerdot\ \ \overrightarrow{AC}=\vec{v}$, on dira que le point $C$ est l'image du point $A$ par la translation du vecteur $\vec{v}$ qui est notée
$$t_{\vec{v}}\;;\quad t_{\vec{v}}(A)=C$$
I.2 Propriétés
$\centerdot\ \ \overrightarrow{MM}=\vec{0}$ si l'origine et l'extrémité du vecteur sont confondues alors, on a un vecteur nul noté $\vec{0}.$
$\centerdot\ \ \vec{u}+\vec{0}=\vec{0}+\vec{u}=\vec{u}$, on dira que le vecteur $\vec{0}$ est l'élément neutre de l'addition vectorielle.
$\centerdot\ \ \vec{u}+\vec{v}=\vec{v}+\vec{u}$, on dira que l'addition vectorielle est commutative.
$\centerdot$ $\forall\; \vec{u}$, $\ \vec{v}\ $ et $\ \vec{w}$ trois vecteurs on a : $\vec{u}+\vec{v}+\vec{w}=(\vec{v}+\vec{u})+\vec{w}=\vec{v}+(\vec{u}+\vec{w})$
$\centerdot\ \ \overrightarrow{AB}=-\overrightarrow{BA}$
$\centerdot\ \ $ Relation de Chasles : $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\;;\quad\forall\;A\;,\ B\ $ et $\ C$
II. Multiplication d'un vecteur par un réel
Activité
Sur un axe gradué, placer $A\ $ et $\ B$ tels que $x_{A}=0\ $ et $\ x_{B}=1$. Posons $\vec{u}=\overrightarrow{AB}.$
1) Placer les points $M$, $\ N\ $ et $\ P$ d'abscisses respectives $-2\;,\ 3\;,\ 1/2$ puis exprimer $\overrightarrow{AM}$, $\ \overrightarrow{AN}$, $\ \overrightarrow{AP}$, $\ \overrightarrow{MN}$, $\ \overrightarrow{NP}$ en fonction de $\vec{u}.$
2) Construire $C$ tel que $\overrightarrow{AC}=2\vec{u}\ $ et $\ D$ tel que $\overrightarrow{AD}=-3\vec{u}.$
Résolution
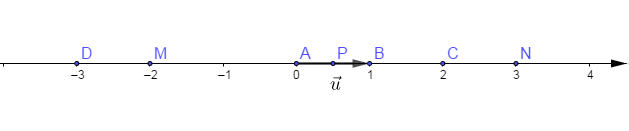
$\overrightarrow{AM}=-2\vec{u}\;,\quad \overrightarrow{AN}=3\vec{u}\;,\quad \overrightarrow{AP}=\dfrac{1}{2}\vec{u}\;,\quad \overrightarrow{MN}=5\vec{u}\;,\quad \overrightarrow{NP}=-\dfrac{5}{2}\vec{u}$
Remarque :
$A$ est l'origine et $\overrightarrow{AB}=\vec{u}$ est le vecteur de base. $(A,\ \overrightarrow{AB})$ est un repère de l'axe.
II.1 Définitions
$A$ un point du plan, $\vec{u}$ un vecteur non nul. $B$ l'unique point tel que $\overrightarrow{AB}=\vec{u}.$ Si $M\in(AB) \: \exists\;\alpha\in\mathbb{R}$ tel que $x_{M}=\alpha$
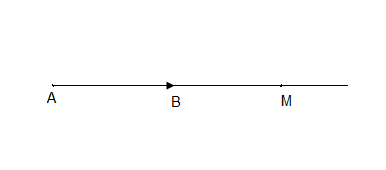
$\overrightarrow{AM}$ est un vecteur produit de $\vec{u}$ par $\alpha$. $\ \overrightarrow{AM}=\alpha.\vec{u}$
$\centerdot\ \ $ Si $\alpha>0 \ $ alors, $\ \overrightarrow{AM}\ $ et $\ \vec{u}$ ont même sens
$\centerdot\ \ $ Si $\alpha<0 \ $ alors, $\ \overrightarrow{AM}\ $ et $\ \vec{u}$ sont de sens contraires
II.2 Propriétés
$\centerdot\ \ \forall\; \vec{u}$ on a $1.\vec{u}=\vec{u}$
$\centerdot\ \ a\;,\ b\in\mathbb{R}$ alors, $a(b\vec{u})=(ab)\vec{u}$
$\centerdot\ \ (a+b)\vec{u}=a.\vec{u}+b.\vec{u} \quad$ $\forall\; a, b\in\mathbb{R}$
$\centerdot\ \ \forall\; a\in\mathbb{R} \quad a(\vec{u}+\vec{v})=a.\vec{u}+a.\vec{v}$
$\centerdot\ \ \forall\; k\in\mathbb{R} \quad k.\vec{u}=\vec{0}$ $\Leftrightarrow$ $\ k=0\ $ ou $\ \vec{u}=\vec{0}$
II.3 Vecteurs colinéaires
II.3.1 Définitions
Deux vecteurs $\vec{u}\ $ et $\ \vec{v}$ sont colinéaires si l'un est le produit de l'autre vecteur par un réel $k$. Donc, $\vec{u}\ $ et $\ \vec{v}$ sont colinéaires si, et seulement si, il existe un réel $k$ tel que $$\vec{u}=k.\vec{v}$$
II.3.2 Remarques
$\centerdot\ \ $ Le vecteur nul est colinéaire à tout vecteur.
$\centerdot\ \ $ Trois points $M$, $\ N\ $ et $\ P$ sont alignés $\Rightarrow \overrightarrow{MN}$ est colinéaire à $\overrightarrow{MP}.$
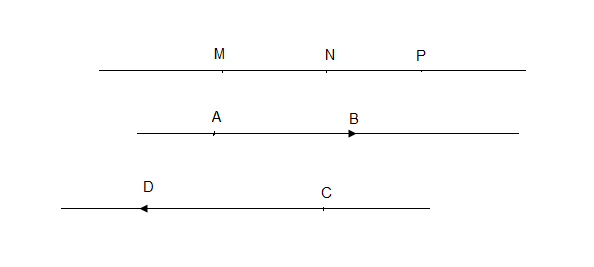
Les droites $(AB)\ $ et $\ (CD)$ sont parallèles si, et seulement si, les vecteurs $\overrightarrow{AB}\ $ et $\ \overrightarrow{CD}$ sont colinéaires.
Exercice d'application
Soit $ABC$ un triangle, $E$ le point défini par : $$3\overrightarrow{EA}+\overrightarrow{EB}=\vec{0}$$
1) Construire le point $E$
2) Construire le point $F$ tel que $\overrightarrow{EF}=\dfrac{1}{4}\overrightarrow{BC}$
3) Montrer que les points $A\;,\ C$ et $F$ sont alignés.
Résolution
1) On a :
$\begin{array}{rcl} 3\overrightarrow{EA}+\overrightarrow{EB}=\vec{0}&\Rightarrow&3\overrightarrow{EA}+\overrightarrow{EA}+\overrightarrow{AB}=\vec{0}\\ \\&\Rightarrow&4\overrightarrow{EA}+\overrightarrow{AB}=\vec{0}\\ \\&\Rightarrow&-4\overrightarrow{AE}+\overrightarrow{AB}=\vec{0}\\ \\&\Rightarrow&4\overrightarrow{AE}=\overrightarrow{AB}\\ \\&\Rightarrow&\overrightarrow{AE}=\dfrac{1}{4}\overrightarrow{AB} \end{array}$
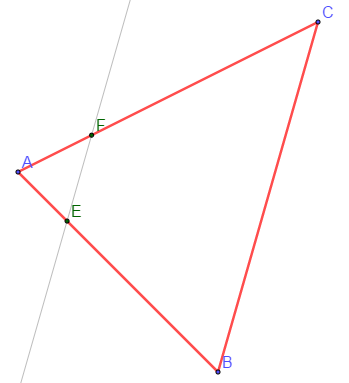
3) $A\;,\ C\ $ et $\ F$ sont alignés si, et seulement si, $\overrightarrow{AC}$ colinéaire à $\overrightarrow{AF}$, c'est à dire $\overrightarrow{AC}=k\overrightarrow{AF}\;,\ k\in\mathbb{R}^{*}$
On a :
$\begin{array}{rcl} \overrightarrow{AC}&=&\overrightarrow{AB}+\overrightarrow{BC}\quad \text{or }\overrightarrow{AB}=4\overrightarrow{AE}\ \text{ et }\overrightarrow{BC}=4\overrightarrow{EF}\\ \\&=&4\overrightarrow{AE}+4\overrightarrow{EF}\\ \\&=&4(\overrightarrow{AE}+\overrightarrow{EF})\\ \\&=&4\overrightarrow{AF} \end{array}$
$\overrightarrow{AC}=4\overrightarrow{AF}$ donc les points $A\;,\ C\ $ et $\ F$ sont alignés.
III. Vecteurs de base du plan
III.1 Définitions
Deux vecteurs $\vec{u}\ $ et $\ \vec{v}$ non colinéaires forment une base du plan vectoriel. Donc quelque soit le vecteur $\vec{w}$, il existe deux réels $\alpha$ et $\beta$ tels que $\vec{w}=\alpha\vec{u}+\beta\vec{v}$. $\ \alpha\ $ et $\ \beta$ sont les coordonnées de $\vec{w}$ dans la base $(\vec{u},\ \vec{v}).$
Si $A$ est un point du plan, le triplet $(A;\ \vec{u},\ \vec{v})$ sera un repère du plan $\mathcal{P}.$
$\forall\; M\in\mathcal{P} \quad \exists \: x\ $ et $\ y$ des réels tels que
$$\overrightarrow{AM}=x\vec{u}+y\vec{v}$$
$$\overrightarrow{AM}=x\vec{u}+y\vec{v}$$
$A$ est l'origine des vecteurs.
$\vec{u}\ $ et $\ \vec{v}$ sont les vecteurs de base du repère.
Si $\vec{u}\ $ et $\ \vec{v}$ sont orthogonaux, on dira que le repère $(A;\ \vec{u},\ \vec{v})$ est orthogonal.
III.2 Condition de colinéarité de deux vecteurs
$\vec{a}\begin{pmatrix}
x\\
y
\end{pmatrix}$, $\vec{b}\begin{pmatrix}
x'\\
y'
\end{pmatrix}$ dans le plan muni du repère $(A;\ \vec{u},\ \vec{v})$ sont colinéaires si et seulement si $$xy'-x'y=0$$
x\\
y
\end{pmatrix}$, $\vec{b}\begin{pmatrix}
x'\\
y'
\end{pmatrix}$ dans le plan muni du repère $(A;\ \vec{u},\ \vec{v})$ sont colinéaires si et seulement si $$xy'-x'y=0$$
III.3 Condition d'orthogonalité de vecteurs
$(A;\ \vec{u},\ \vec{v})$ repère orthonormé, $\vec{a}\begin{pmatrix}
x\\
y
\end{pmatrix}$, $\vec{b}\begin{pmatrix}
x'\\
y'
\end{pmatrix}$ sont orthogonaux si et seulement si $$xx'+yy'=0$$
x\\
y
\end{pmatrix}$, $\vec{b}\begin{pmatrix}
x'\\
y'
\end{pmatrix}$ sont orthogonaux si et seulement si $$xx'+yy'=0$$
III.4 Norme d'un vecteur - Distance entre deux vecteurs
III.4.1 Définitions
$A$ un point du plan, $\vec{u}$ un vecteur non nul et $B$ l'unique point tel que $\overrightarrow{AB}=\vec{u}.$
On appelle norme du vecteur $\vec{u}$ notée $||\vec{u}||$ la longueur de $[AB]$ qui est la distance entre $A\ $ et $\ B$ notée $d(A,\ B)$ $$||\vec{u}||=d(A, B)=||\overrightarrow{AB}||=AB$$
Si $||\vec{u}||=1$, on dit que le vecteur est unitaire ou que le vecteur est normé.
III.4.2 Expression dans un repère orthonormé
$\left(A;\ \vec{u},\ \vec{v}\right)$ repère orthonormé tel que $||\vec{u}||=||\vec{v}||=1$ et $\vec{u}\perp\vec{v}$.
Soit $\vec{a}\begin{pmatrix} x\\y\end{pmatrix}$. On a $||\vec{a}||=\sqrt{x^{2}+y^{2}}$.
De même, en considérant les points $A\begin{pmatrix}
x_{A}\\
y_{A}
\end{pmatrix}$ et $B\begin{pmatrix}
x_{B}\\
y_{B}
\end{pmatrix}$ nous obtenons $$||\overrightarrow{AB}||=d(A,\ B)=AB=\sqrt{(x_{B}-x_{A})^{2}+(y_{B}-y_{A})^{2}}$$
IV. Vecteurs de configurations géométriques
IV.1 Milieu d'un segment et centre de gravité d'un triangle
Activité 1
Soient $A\ $ et $\ B$ deux points du plan, $I$ milieu de $[AB].$
1) Déterminer la relation entre $\overrightarrow{AB}$ et $\overrightarrow{AI}\;$, $\ \overrightarrow{AB}$ et $\overrightarrow{BI}\;$, $\ \overrightarrow{IA}$ et $\overrightarrow{IB}\;$, $\ \overrightarrow{BA}\ $ et $\ \overrightarrow{IA}$
2) Montrer que $\forall\;M\;;\quad \overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}$
Résolution
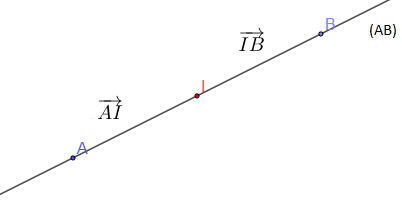
1) Nous avons :
$\overrightarrow{AB}=2\overrightarrow{AI}\;,\ \overrightarrow{AB}=-2\overrightarrow{BI}\;,\ \overrightarrow{IA}=\overrightarrow{IB}$ et $\overrightarrow{BA}=2\overrightarrow{IA}$
2)
$\begin{array}{rcl} \forall\;M\;;\quad \overrightarrow{MA}+\overrightarrow{MB}&=&\overrightarrow{MI}+\overrightarrow{IA}+\overrightarrow{MI}+\overrightarrow{IB}\\ \\&=&2\overrightarrow{MI}+\underbrace{\overrightarrow{IA}+\overrightarrow{IB}}_{\vec{0}}\quad\text{car }I\text{ milieu de }[AB]\\ \\&=&2\overrightarrow{MI} \end{array}$
Activité 2
Soit $ABC$ un triangle de centre de gravité $G\ $ et $\ I$ milieu de $[BC].$
1) Rappeler la définition du centre de gravité.
2) a) Exprimer $\overrightarrow{GA}$ en fonction de $\overrightarrow{GI}$, puis $\overrightarrow{GA}$ en fonction de $\overrightarrow{AI}.$
b) En déduire que $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\vec{0}.$
c) Montrer que $\forall\;M\;;\quad \overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}$
Résolution
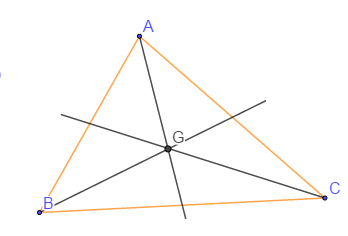
1) On appelle centre de gravité d'un triangle, le point de rencontre des trois médianes.
2) a) $\overrightarrow{GA}=-2\overrightarrow{GI}$ et $\overrightarrow{GA}=-\dfrac{2}{3}\overrightarrow{AI}$
b)
$\begin{array}{rcl} \overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}&=&\overrightarrow{GA}+\overrightarrow{GI}+\overrightarrow{IB}+\overrightarrow{GI}+\overrightarrow{IC}\\ \\&=&\overrightarrow{GA}+2\overrightarrow{GI}+\underbrace{\overrightarrow{IB}+\overrightarrow{IC}}_{\vec{0}}\quad\text{car }I\text{ milieu de }[BC]\\ \\&=&-2\overrightarrow{GI}+2\overrightarrow{GI}\\ \\&=&\vec{0}\end{array}$
c)
$\begin{array}{rcl} \forall\;M\;;\quad \overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}&=&\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}\\ \\ &=&3\overrightarrow{MG}+\underbrace{\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}}_{\vec{0}}\\ \\&=&3\overrightarrow{MG}\end{array}$
IV.2 Théorème de Thalès (Forme vectorielle)
$ABC$ un triangle, $I\in[AB]\ $ et $\ J\in[AC]$ tels que $(IJ)//(BC)$
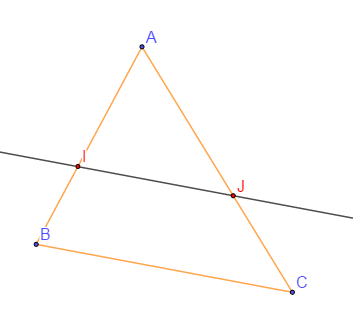
D'après théorème de Thalès on a : $$\dfrac{AI}{AB}=\dfrac{AJ}{AC}=\dfrac{IJ}{BC}=k$$
Auteur:
Diny Faye & Seyni Ndiaye

Commentaires
Anonyme (non vérifié)
mar, 09/29/2020 - 15:32
Permalien
c'est un cours bien et qui
Kientega Youba (non vérifié)
lun, 10/05/2020 - 08:04
Permalien
J'AI
Anonyme (non vérifié)
mer, 11/11/2020 - 20:25
Permalien
Merci
M Pouye (non vérifié)
lun, 01/11/2021 - 07:05
Permalien
Le cous est intéressant
Modou Dieng (non vérifié)
dim, 02/07/2021 - 23:37
Permalien
Merci
Fallou Ndiaye (non vérifié)
lun, 02/08/2021 - 10:59
Permalien
Etud
M Ndiaye (non vérifié)
mer, 02/17/2021 - 08:29
Permalien
Document
Anonyme (non vérifié)
sam, 02/20/2021 - 09:29
Permalien
Bjr,
Anonyme (non vérifié)
dim, 03/07/2021 - 15:51
Permalien
c bien ce que vous faite
Anonyme (non vérifié)
sam, 11/20/2021 - 16:58
Permalien
Bon doc
diallomamoudoum... (non vérifié)
ven, 11/04/2022 - 14:04
Permalien
merci beaucoup
Ali Lom (non vérifié)
sam, 09/13/2025 - 22:21
Permalien
Un cours bien fait
Rokhaya (non vérifié)
mer, 11/05/2025 - 07:34
Permalien
C'est mieux comme ça bien
Ajouter un commentaire