I Primitive
I.1 Définition
Soit $I$ un intervalle de $\mathbb{R}\ $ et $\ f$ une fonction continue sur $I.$ On dit que $F$ est une primitive de $f$ sur $I$ notée $\int f$ si, $$F\ \text{ est dérivable sur }I\ \text{ et }\ \forall\;x\in I\;,\ F'(x)=f(x)$$
Exemple
Soit $f\ $ et $\ F$ deux fonctions définies par :
$f(x)=x^{2}\;,\quad F(x)=\left\lbrace\begin{array}{rcl} \dfrac{1}{3}x^{3}&\text{si}&x\leq 0 \\ \\ \dfrac{1}{3}x^{3}-1&\text{si}&x>0\end{array}\right.$
$F$ est-elle une primitive de $f$ sur :
$]-\infty\;,\ 0]\ ?\;,\quad[0\;,\ +\infty[\ ?\;,\quad]0\;,\ +\infty[\ ?\;,\quad\mathbb{R}\ ?$
Résolution
$\begin{array}{rcl}\lim\limits_{x\to 0^{-}}\dfrac{F(x)-F(0)}{x-0}&=&\lim\limits_{x\rightarrow 0^{-}}\dfrac{\dfrac{1}{3}x^{3}}{x}\\ \\&=&\lim\limits_{x\to 0^{-}}\dfrac{1}{3}x^{2}\\\ \\&=&0\end{array}$
Donc, $F$ est dérivable à gauche de $0.$
$\begin{array}{rcl}\lim\limits_{x\to 0^{+}}\dfrac{F(x)-F(0)}{x-0}&=&\lim\limits_{x\to 0^{+}}\dfrac{\dfrac{1}{3}x^{3}-1}{x}\\ \\&=&\lim\limits_{x\to 0^{+}}\dfrac{1}{3}x^{2}-\dfrac{1}{x}\\ \\&=&-\infty\end{array}$
Donc, $F$ n'est pas dérivable à droite de $0.$
$F$ est dérivable sur $]-\infty\;,\ 0]$ et $F'(x)=x^{2}=f(x)$, donc $F$ est une primitive de $f$ sur $]-\infty\;,\ 0].$
$F$ n'est pas dérivable sur $[0\;,\ +\infty[$, donc $F$ n'est pas une primitive de $f$ sur $[0\;,\ +\infty[.$
$F$ est dérivable sur $]0\;,\ +\infty[$ et $F'(x)=f(x)$, donc $F$ est une primitive de $f$ sur $]0\;,\ +\infty[.$
$F$ non dérivable sur $\mathbb{R}$, donc $F$ n'est pas une primitive de $f$ sur $\mathbb{R}.$
Théorème 1
Toute fonction continue sur $I$ y admet une primitive.
Théorème 2
Si $F$ est une primitive de $f$ sur $I$, alors toute fonction $G$ définie par $$G(x)=F(x)+c\;;\quad c\ \text{ une constante}$$ est aussi une primitive de $f$ sur $I.$
Donc deux primitives quelconques d'une fonction diffèrent d'une constante et il existe une unique primitive qui prend une valeur $y$ en $x_{0}.$
Théorème 3
Soit $f$ une fonction dérivable sur $I$ de dérivée $f'$ continue sur $I$ et $g$ une fonction continue sur $I$ de primitive $G$ définie sur un intervalle $J$ contenant $f(I)$, alors $(g\circ f)f'$ a pour primitive sur $I\;,\ G\circ f$
I.2 Opération sur les primitives
Si $F$ est une primitive de $f$ et $G$ une primitive de $g$, alors
$\alpha F+\beta G$ est une primitive de $\alpha f+\beta g\;;\quad\alpha\;,\ \beta\in\mathbb{R}$
Tableau de quelques primitives
$u$ et $v$ sont deux fonctions continues et $c$ une constante.
$$\begin{array}{|c|c|}\hline f&F \\ \hline a\in\mathbb{R}&ax+c \\ \hline\dfrac{1}{x}\;;\ x>0&\ln|x|+c \\ \hline\mathrm{e}^{x}&\mathrm{e}^{x} \\ \hline\sin x&-\cos x+c \\ \hline\cos x&\sin x+c \\ \hline\dfrac{1}{\sqrt{x}}\;;\ x>0&2\sqrt{x} \\ \hline\dfrac{1}{x^{2}}\;;\ x>0&-\dfrac{1}{x} \\ \hline\end{array}\quad\begin{array}{|c|c|}\hline f&F \\ \hline x^{n}&\dfrac{x^{n+1}}{n+1}+c \\ \hline\dfrac{1}{\cos^{2}x}=1+\tan^{2}x&\tan x \\ \hline u'u^{n}&\dfrac{u^{n+1}}{n+1} \\ \hline \dfrac{u'}{u}&\ln|u| \\ \hline u'\mathrm{e}^{u}&\mathrm{e}^{u} \\ \hline\dfrac{u'}{u^{2}}&-\dfrac{1}{u} \\ \hline \end{array}$$
$$\begin{array}{|c|c|}\hline f&F \\ \hline u'\cos u&\sin u \\ \hline u'\sin u&-\cos u \\ \hline\dfrac{u'}{\cos^{2}u}=1+\tan^{2}u&\tan u \\ \hline\dfrac{u'}{\sqrt{u}}&2\sqrt{u} \\ \hline u'v+v'u&uv \\ \hline\lambda f\;;\ \lambda\in\mathbb{R}&\lambda F \\ \hline\dfrac{u'v-uv'}{v^{2}}&\dfrac{u}{v} \\ \hline \end{array}$$
Théorème
Si $u$ et $v$ sont dérivables sur $I$ de dérivées $u'$ et $v'$ continues sur $I$, alors $$\int u'v=uv-\int uv'$$
En effet, \begin{eqnarray} (uv)'=u'v+v'u&\Rightarrow&u'v=(uv)'-uv'\nonumber\\ \\&\Rightarrow&\int u'v=\int(uv)'-\int uv'\nonumber\\ \\&\Rightarrow&\int u'v=uv-\int uv'\nonumber\end{eqnarray}
Exemple
Déterminer les primitives de :
$f(x)=x\cos x\;,\quad g(x)=x\mathrm{e}^{x}\;,\quad h(x)=\ln x$
Résolution
Posons $u'=\cos x\ \Rightarrow\ u=\sin x\ $ et $\ v=x\ \Rightarrow\ v'=1$ donc, \begin{eqnarray} \int f(x)&=&F(x)\nonumber \\ \\&=&x\sin x-\int\sin x\nonumber \\ \\&=&x\sin x+\cos x\nonumber \end{eqnarray}
On pose : $u'=\mathrm{e}^{x}\ \Rightarrow\ u=\mathrm{e}^{x}\ $ et $\ v=x\ \Rightarrow\ v'=1$ alors, \begin{eqnarray} \int g(x)&=&G(x)\nonumber \\ \\&=&x\mathrm{e}^{x}-\int\mathrm{e}^{x}\nonumber \\ \\&=&x\mathrm{e}^{x}-\mathrm{e}^{x}\nonumber \end{eqnarray}
Posons : $u=x\ \Rightarrow\ u'=1\ $ et $\ v=\ln x\ \Rightarrow\ v'=\dfrac{1}{x}$ alors, \begin{eqnarray} \int h(x)&=&H(x)\nonumber \\ \\&=&x\ln x-\int 1\nonumber \\ \\&=&x\ln x-x\nonumber \end{eqnarray}
II Définition et propriétés
II.1 Définition
Soit $I$ un intervalle de $\mathbb{R}\;,\ a\;,\ b\in I$ et $f$ une fonction continue sur $I.$ On appelle intégrale de $a$ à $b$ de $f$ le réel noté $$\int_{a}^{b}f(x)\mathrm{d}x=\left[F(x)\right]_{a}^{b}=F(b)-F(a)$$
où $F$ est une primitive quelconque de $f$ sur $[a\;,\ b]$ ou $[b\;,\ a]$
Remarques
$\centerdot\ \ $ Le choix de la primitive $F$ n'influe pas le résultat de l'intégrale. En effet, si $F$ et $G$ sont deux primitives d'une même fonction $f$ sur $I$, alors elles différent d'une constante. Les quantités $F(b)-F(a)$ et $G(b)-G(a)$ sont donc égales. \begin{eqnarray} \text{Soit }G(x)=F(x)+c\;,\ \text{ alors }\int_{a}^{b}f(x)\mathrm{d}x&=&\left[G(x)\right]_{a}^{b}\nonumber \\ \\&=&G(b)-G(a)\nonumber \\ \\&=&F(b)+c-(F(a)+c)\nonumber \\ \\&=&F(b)-F(a)\nonumber \end{eqnarray}
$\centerdot\ \ $ Soit $I$ un intervalle et $x_{0}\in I$, Pour tout réel $x$ de $I$, nous avons : $$\int_{x_{0}}^{x}f(t)\mathrm{d}t=\left[F(t)\right]_{x_{0}}^{x}=F(x)-F(x_{0})$$ La fonction $\mathcal{F}$ définie sur $I$ par $$\mathcal{F}(x)=\int_{x_{0}}^{x}f(t)\mathrm{d}t$$ est donc la primitive de $f$ sur $I$ qui s'annule en $x_{0}.$
$\centerdot\ \ $ La lettre $t$ ( ou $x$) choisie pour la variable est une variable "muette" ; elle peut être notée par toute autre lettre. Ce qui signifie que : $$\int_{a}^{b}f(x)\mathrm{d}x=\int_{a}^{b}f(t)\mathrm{d}t=\int_{a}^{b}f(u)\mathrm{d}u=F(b)-F(a)$$
Exemple
Calculer $$I=\int_{4}^{5}\dfrac{1}{x^{2}-9}\mathrm{d}x\;,\quad J=\int_{0}^{1}\dfrac{x}{x+1}\mathrm{d}x\;,\quad K=\int_{1}^{\mathrm{e}}\dfrac{\ln x}{x}\mathrm{d}x$$
Résolution
Soit $I=\int_{4}^{5}\dfrac{1}{x^{2}-9}\mathrm{d}x$.
On a : $\dfrac{1}{x^{2}-9}=\dfrac{1}{(x-3)(x+3)}=\dfrac{1}{6(x-3)}-\dfrac{1}{6(x+3)}$, alors \begin{eqnarray} I&=&\int_{4}^{5}\dfrac{1}{x^{2}-9}\mathrm{d}x\nonumber \\ \\&=&\int_{4}^{5}\left(\dfrac{1}{6(x-3)}-\dfrac{1}{6(x+3)}\right)\mathrm{d}x\nonumber \\ \\&=&\left[\dfrac{1}{6}\ln|x-3|-\dfrac{1}{6}\ln|x+3|\right]_{4}^{5}\nonumber \\ \\&=&\dfrac{1}{6}\ln 2-\dfrac{1}{6}\ln 8-\left(\dfrac{1}{6}\ln 1-\dfrac{1}{6}\ln 7\right)\nonumber \\ \\&=&\dfrac{1}{6}\ln 2-\dfrac{1}{6}\ln 2^{3}+\dfrac{1}{6}\ln 7\nonumber \\ \\&=&\dfrac{1}{6}\ln 2-\dfrac{3}{6}\ln 2+\dfrac{1}{6}\ln 7\nonumber \\ \\&=&-\dfrac{1}{3}\ln 2+\dfrac{1}{6}\ln 7\nonumber \end{eqnarray}
Donc, $$I=\int_{4}^{5}\dfrac{1}{x^{2}-9}\mathrm{d}x=-\dfrac{1}{3}\ln 2+\dfrac{1}{6}\ln 7$$
$J=\int_{0}^{1}\dfrac{x}{x+1}\mathrm{d}x.\ \text{ Or}\;,\ \dfrac{x}{x+1}=1-\dfrac{1}{x+1}$ donc, \begin{eqnarray} J&=&\int_{0}^{1}\dfrac{x}{x+1}\mathrm{d}x\nonumber \\ \\&=&\int_{0}^{1}\left(1-\dfrac{1}{x+1}\right)\mathrm{d}x\nonumber \\ \\&=&\left[x-\ln|x+1|\right]_{0}^{1}\nonumber \\ \\&=&1-\ln 2\nonumber \end{eqnarray}
Donc $$J=\int_{0}^{1}\dfrac{x}{x+1}\mathrm{d}x=1-\ln 2$$
\begin{eqnarray} K&=&\int_{1}^{\mathrm{e}}\dfrac{\ln x}{x}\mathrm{d}x\nonumber \\ \\&=&\left[\dfrac{1}{2}\ln^{2}|x|\right]_{1}^{\mathrm{e}}\nonumber \\ \\&=&\dfrac{1}{2}\ln^{2}\mathrm{e}-0\nonumber\\ \\&=&\dfrac{1}{2}\nonumber \end{eqnarray}
Donc, $$K=\int_{1}^{\mathrm{e}}\dfrac{\ln x}{x}\mathrm{d}x=\dfrac{1}{2}$$
II.2 Propriétés
Soit $I$ un intervalle de $\mathbb{R}\;,\ a\;,\ b\;,\ c\in I\;,\ f$ et $g$ deux fonctions continues sur $I\;,\ \alpha\;,\ \beta\in\mathbb{R}$, alors
$\centerdot\ \ $ $$\int_{a}^{a}f(x)\mathrm{d}x=0$$
$\centerdot\ \ $ $$\int_{a}^{b}f(x)\mathrm{d}x=-\int_{b}^{a}f(x)\mathrm{d}x$$
$\centerdot\ \ $ Relation de Chasles $$\int_{a}^{b}f(x)\mathrm{d}x=\int_{a}^{c}f(x)\mathrm{d}x+\int_{c}^{b}f(x)\mathrm{d}x$$
$\centerdot\ \ $ Linéarité de l'intégration $$\int_{a}^{b}(\alpha f+\beta g)(x)\mathrm{d}x=\alpha\int_{a}^{b}f(x)\mathrm{d}x+\beta\int_{a}^{b}g(x)\mathrm{d}x$$
$\centerdot\ \ $ Si $f$ est paire, alors $$\int_{-a}^{a}f(x)\mathrm{d}x=2\int_{0}^{a}f(x)\mathrm{d}x$$
$\centerdot\ \ $ Si $f$ est impaire, alors $$\int_{-a}^{a}f(x)\mathrm{d}x=0$$
$\centerdot\ \ $ Si $f$ est périodique de période $T$, alors $$\int_{a}^{a+T}f(x)\mathrm{d}x=\int_{0}^{T}f(x)\mathrm{d}x$$
$\centerdot\ \ $ Positivité de l'intégration : Si $a\leq b$ et $f\geq 0$ sur $[a\;,\ b]$, alors $$\int_{a}^{b}f(x)\mathrm{d}x\geq 0$$
$\centerdot\ \ $ Conservation de l'ordre de l'intégration : Si $a\leq b$ et $f\leq g$ sur $[a\;,\ b]$, alors $$\int_{a}^{b}f(x)\mathrm{d}x\leq\int_{a}^{b}g(x)\mathrm{d}x$$
$\centerdot\ \ $ $$\left|\int_{a}^{b}f(x)\mathrm{d}x\right|\leq\int_{a}^{b}|f(x)|\mathrm{d}x$$
$\centerdot\ \ $ Inégalité de la moyenne : La fonction $f$ étant continue sur $[a\;,\ b]$, alors il existe deux réels $m$ et $M$ tels que, pour tout réel $x\in[a\;,\ b]$ on ait $m\leq f(x)\leq M$ et donc : $$m(b-a)\leq\int_{a}^{b}f(x)\mathrm{d}x\leq M(b-a)$$
En effet \begin{eqnarray} m\leq f(x)\leq M&\Rightarrow&\int_{a}^{b}m\mathrm{d}x\leq\int_{a}^{b}f(x)\mathrm{d}x\leq\int_{a}^{b}M\mathrm{d}x\nonumber \\ \\&\Rightarrow&m(b-a)\leq\int_{a}^{b}f(x)\mathrm{d}x\leq M(b-a)\nonumber \end{eqnarray}
Théorème de la moyenne
Pour toute fonction $f$ définie et continue sur l'intervalle $[a\;,\ b]$, d'après le théorème des valeurs intermédiaires, il existe au moins un réel $c\in[a\;,\ b]$ tel que
$$f(c)=\dfrac{1}{b-a}\int_{a}^{b}f(x)\mathrm{d}x$$ Le réel $f(c)$ est appelé valeur moyenne de $f$ sur $[a\;,\ b].$
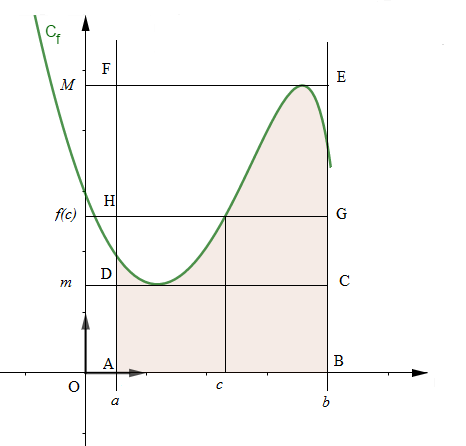
Interprétations géométriques
Le plan est muni d'un repère orthogonal $(O\;;\ \vec{i}\;,\ \vec{j})$. Soit $f$ une fonction continue et positive de courbe représentative $(C_{f})$, alors
$\centerdot\ \ $ L'encadrement $$m(b-a)\leq\int_{a}^{b}f(x)\mathrm{d}x\leq M(b-a)$$ signifie que l'aire du domaine coloré est minorée par l'aire du rectangle $ABCD$, et majorée par celle du rectangle $ABEF.$
$\centerdot\ \ $ L'égalité $$f(c)=\dfrac{1}{b-a}\int_{a}^{b}f(x)\mathrm{d}x$$ signifie que l'aire du domaine coloré est égale à celle du rectangle $ABGH.$
Exercice d'application
Soit la suite $(u_{n})$ définie par $$u_{n}=\int_{1}^{\mathrm{e}}x(\ln x)^{n}\mathrm{d}x$$ Montrer que $u_{n}$ est décroissante.
Résolution
\begin{eqnarray} u_{n+1}-u_{n}&=&\int_{1}^{\mathrm{e}}x(\ln x)^{n+1}\mathrm{d}x-\int_{1}^{\mathrm{e}}x(\ln x)^{n}\mathrm{d}x\nonumber \\ \\&=&\int_{1}^{\mathrm{e}}\left(x(\ln x)^{n+1}-x(\ln x)^{n}\right)\mathrm{d}x\nonumber \\ \\&=&\int_{1}^{\mathrm{e}}x(\ln x)^{n}(\ln x-1)\mathrm{d}x\nonumber \end{eqnarray}
Or, $x\leq\mathrm{e}\ \Rightarrow\ \ln x\leq 1$, donc $\ln x-1\leq 0$. De plus $x(\ln x)^{n}>0.$
Alors, $x(\ln x)^{n}(\ln x-1)<0$ et donc $$\int_{1}^{\mathrm{e}}x(\ln x)^{n}(\ln x-1)\mathrm{d}x<0$$ d'où $u_{n+1}-u_{n}<0$ ce qui signifie que $(u_{n})$ est décroissante.
III Méthodes d'intégration
III.1 A l'aide du tableau de primitives
Exemple
Calculer $$I=\int_{0}^{1}x\sqrt{1-x^{2}}\mathrm{d}x\;,\quad J=\int_{0}^{\tfrac{\pi}{6}}\sin 2x\cos 3x\mathrm{d}x$$
Posons $u=1-x^{2}\ \Rightarrow\ u'=-2x$, donc $x\sqrt{1-x^{2}}=-\dfrac{1}{2}u'u^{1/2}.$
Or, $u'u^{1/2}$ a pour primitive $\dfrac{2}{3}u^{3/2}$ donc $-\dfrac{1}{2}\left(\dfrac{2}{3}u^{3/2}\right)=-\dfrac{1}{3}u^{3/2}$ est primitive de $-\dfrac{1}{2}u'u^{1/2}.$
Donc, \begin{eqnarray} I&=&\int_{0}^{1}x\sqrt{1-x^{2}}\mathrm{d}x\nonumber \\ \\&=&\left[-\dfrac{1}{3}(1-x^{2})\sqrt{1-x^{2}}\right]_{0}^{1}\nonumber \\ \\&=&\dfrac{1}{3}\nonumber \end{eqnarray}
On a : $\sin 2x\cos 3x=\dfrac{1}{2}[\sin 5x+\sin(-x)]$ donc, \begin{eqnarray} J&=&\int_{0}^{\tfrac{\pi}{6}}\sin 2x\cos 3x\mathrm{d}x\nonumber \\ \\&=&\int_{0}^{\tfrac{\pi}{6}}\left(\dfrac{1}{2}\sin 5x-\dfrac{1}{2}\sin x\right)\mathrm{d}x\nonumber \\ \\&=&\left[-\dfrac{1}{10}\cos 5x+\dfrac{1}{2}\cos x\right]_{0}^{\tfrac{\pi}{6}}\nonumber \\ \\&=&\dfrac{\sqrt{3}}{20}+\dfrac{\sqrt{3}}{4}+\dfrac{1}{10}-\dfrac{1}{2}\nonumber \\ \\&=&\dfrac{6\sqrt{3}}{20}-\dfrac{4}{10}\nonumber \end{eqnarray}
Donc, $$J=\int_{0}^{\tfrac{\pi}{6}}\sin 2x\cos 3x\mathrm{d}x=\dfrac{3\sqrt{3}}{10}-\dfrac{2}{5}$$
III.2 A l'aide de la linéarisation
Exemple
Calculer $$I=\int_{0}^{\pi}\sin^{5}x\mathrm{d}x$$
On a $\sin^{5}x=\left(\dfrac{\mathrm{e}^{\mathrm{i}x}-\mathrm{e}^{-\mathrm{i}x}}{2\mathrm{i}}\right)^{5}$,
après développement (chapitre - nombres complexes) on obtient $\sin^{5}x=\dfrac{1}{16}\left(\sin 5x-5\sin 3x+10\sin x\right)$,
donc, \begin{eqnarray} I&=&\int_{0}^{\pi}\sin^{5}x\mathrm{d}x\nonumber \\ \\&=&\int_{0}^{\pi}\dfrac{1}{16}\left(\sin 5x-5\sin 3x+10\sin x\right)\mathrm{d}x\nonumber \\ \\&=&\left[-\dfrac{1}{80}\cos 5x+\dfrac{5}{48}\cos 3x-\dfrac{5}{8}\cos x\right]_{0}^{\pi}\nonumber \\ \\&=&\dfrac{1}{80}-\dfrac{5}{48}+\dfrac{5}{8}+\dfrac{1}{80}-\dfrac{5}{48}+\dfrac{5}{8}\nonumber \\ \\&=&\dfrac{1}{40}-\dfrac{5}{24}+\dfrac{5}{4}\nonumber \end{eqnarray}
III.3 Par changement de variables
Théorème
Si $g$ est continue sur $[a\;,\ b]$ et de dérivée $g'$ continue sur $[a\;,\ b].$
Si $f$ est continue sur $[\alpha\;,\ \beta]$ avec $\alpha=g(a)$ et $\beta=g(b)$, alors $$\int_{a}^{b}f\circ g(x)g'(x)\mathrm{d}x=\int_{\alpha}^{\beta}f(u)\mathrm{d}u$$
Exemple
Calculer $$A=\int_{0}^{\tfrac{\pi}{4}}\tan x\mathrm{d}x\;,\quad B=\int_{0}^{\pi}\sin x\cos^{4}x\mathrm{d}x$$
Résolution
Soit $$A=\int_{0}^{\tfrac{\pi}{4}}\tan x\mathrm{d}x=\int_{0}^{\tfrac{\pi}{4}}\dfrac{\sin x}{\cos x}\mathrm{d}x$$
Posons : $u=\cos x\ \Rightarrow\ \mathrm{d}u=-\sin x\mathrm{d}x$, alors $u'=\dfrac{\mathrm{d}u}{\mathrm{d}x}\ \Rightarrow\ \mathrm{d}u=u'\mathrm{d}x$ et donc \begin{eqnarray} A&=&\int_{0}^{\tfrac{\pi}{4}}\tan x\mathrm{d}x\nonumber \\ \\&=&\int_{1}^{\tfrac{\sqrt{2}}{2}}-\dfrac{\mathrm{d}u}{u}\nonumber \\ \\&=&[-\ln|u|]_{1}^{\sqrt{2}/2}\nonumber \\ \\&=&-\ln\dfrac{1}{\sqrt{2}}\nonumber \\ \\&=&\ln\sqrt{2}\ =\ \dfrac{1}{2}\ln 2\nonumber \end{eqnarray}
Soit $$B=\int_{0}^{\pi}\sin x\cos^{4}x\mathrm{d}x$$
Posons : $u=\cos x\ \Rightarrow\ \mathrm{d}u=-\sin x\mathrm{d}x$,
alors, \begin{eqnarray} B&=&\int_{0}^{\pi}\sin x\cos^{4}x\mathrm{d}x\nonumber \\ \\&=&\int_{1}^{-1}-u^{4}\mathrm{d}u\nonumber \\ \\&=&\int_{-1}^{1}u^{4}\mathrm{d}u\nonumber \\ \\&=&2\int_{0}^{1}u^{4}\mathrm{d}u\ \text{ car }g(u)=u^{4}\ \text{ est paire}\nonumber \\ \\&=&2\left[\dfrac{1}{5}u^{5}\right]_{0}^{1}\nonumber \\ \\&=&\dfrac{2}{5}\nonumber \end{eqnarray}
Remarque
$$\int_{a}^{b}\alpha f(\alpha t+\beta)\mathrm{d}t=\int_{\alpha a+\beta}^{\alpha b+\beta}f(u)\mathrm{d}u$$
$u=\alpha t+\beta\ \Rightarrow\ \mathrm{d}u=\alpha\mathrm{d}t$
III.4 Intégration par parties
Si $u$ et $v$ sont dérivables sur $I$ de dérivées $u'$ et $v'$ continues sur $I$ et $a\;,\ b\in I$, alors $$\int_{a}^{b}u'(x)v(x)\mathrm{d}x=[u(x)v(x)]_{a}^{b}-\int_{a}^{b}u(x)v'(x)\mathrm{d}x$$
Exemple
Calculer les intégrales suivantes $$A=\int_{0}^{\pi}x\cos x\mathrm{d}x\;,\quad B=\int_{1}^{\mathrm{e}}x\ln x\mathrm{d}x$$
Résolution
Posons : $u'=\cos x\ \Rightarrow\ u=\sin x\ $ et $\ v=x\ \Rightarrow\ v'=1$, donc \begin{eqnarray} A&=&\int_{0}^{\pi}x\cos x\mathrm{d}x\nonumber \\ \\&=&[x\sin x]_{0}^{\pi}-\int_{0}^{\pi}\sin x\mathrm{d}x\nonumber \\ \\&=&0+[\cos x]_{0}^{\pi}\nonumber \\ \\&=&-2\nonumber \end{eqnarray}
On pose $u'=x\ \Rightarrow\ u=\dfrac{x^{2}}{2}\ $ et $\ v=\ln x\ \Rightarrow\ v'=\dfrac{1}{x}$,
alors, \begin{eqnarray} B&=&\int_{1}^{\mathrm{e}}x\ln x\mathrm{d}x\nonumber \\ \\&=&\left[\dfrac{x^{2}}{2}\ln x\right]_{1}^{\mathrm{e}}-\int_{1}^{\mathrm{e}}\dfrac{x}{2}\mathrm{d}x\nonumber \\ \\&=&\dfrac{\mathrm{e}^{2}}{2}-\left[\dfrac{x^{2}}{4}\right]_{1}^{\mathrm{e}}\nonumber \\ \\&=&\dfrac{\mathrm{e}^{2}}{2}-\dfrac{\mathrm{e}^{2}}{4}+\dfrac{1}{4}\nonumber \\ \\&=&\dfrac{\mathrm{e}^{2}+1}{4}\nonumber \end{eqnarray}
IV Calcul approché d'une intégrale
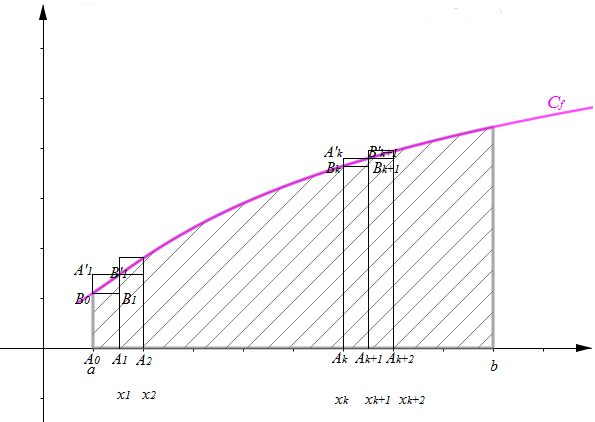
Méthode des rectangles
Soit $I=[a\;,\ b]$ un intervalle $(a<b)$ de $\mathbb{R}\;,\ f$ une fonction continue strictement croissante et positive sur $I.$
$\int_{a}^{b}f(x)\mathrm{d}x$ est la surface du plan ou l'aire du domaine comprise entre la courbe $C_{f}$, l'axe $(x'Ox)$ et les droites d'équations $x=a$ et $x=b.$
On subdivise $[a\;,\ b]$ en $n$ segments de même longueur $\dfrac{b-a}{n}$, on a donc :
$x_{0}=a\;,\ x_{1}=a+\dfrac{b-a}{n}\;,\ x_{2}=a+\dfrac{2(b-a)}{n}\;,\ldots\;,\ x_{k}=a+\dfrac{k(b-a)}{n}$ et $x_{n}=a+\dfrac{n(b-a)}{n}=b.$
On a ainsi un découpage régulier de l'intervalle $I$ car $\forall\;k\in[0\;,\ (n-1)]\;,\ x_{k+1}-x_{k}=\dfrac{b-a}{n}.$
Soit $s_{n}$ la somme des aires des rectangles $A_{k}A_{k+1}B_{k+1}B_{k}$ et $\mathcal{S}_{n}$ la somme des aires des rectangles $A_{k}A_{k+1}B'_{k+1}A'_{k}\;,\quad 0\leq k\leq n-1.$
L'aire du domaine sous la courbe est donc encadrée par deux suites adjacentes d'aires de rectangles associés à une subdivision de l'intervalle $[a\;,\ b]$,
on a alors $$s_{n}\leq\int_{a}^{b}f(x)\mathrm{d}x\leq\mathcal{S}_{n}$$ avec : \begin{eqnarray} s_{n}&=&f(a)\left(\dfrac{b-a}{n}\right)+f\left(a+\dfrac{b-a}{n}\right)\times\dfrac{b-a}{n}+\ldots+f\left(a+\dfrac{(n-1)(b-a)}{n}\right)\times\dfrac{b-a}{n}\nonumber \\ \\&=&\dfrac{b-a}{n}\sum_{k=0}^{n-1}f\left(a+\dfrac{k(b-a)}{n}\right)\nonumber \end{eqnarray} donc $$s_{n}=\dfrac{b-a}{n}\sum_{k=0}^{n-1}f\left(a+\dfrac{k(b-a)}{n}\right)$$
\begin{eqnarray} \mathcal{S}_{n}&=&f\left(a+\dfrac{b-a}{n}\right)\times\dfrac{b-a}{n}+f\left(a+\dfrac{2(b-a)}{n}\right)\times\dfrac{b-a}{n}+\ldots+f\left(a+\dfrac{(n-1)(b-a)}{n}\right)\times\dfrac{b-a}{n}+f(b)\times\dfrac{b-a}{n}\nonumber \\ \\&=&\dfrac{b-a}{n}\sum_{k=1}^{n}f\left(a+\dfrac{k(b-a)}{n}\right)\nonumber \end{eqnarray} donc, $$\mathcal{S}_{n}=\dfrac{b-a}{n}\sum_{k=1}^{n}f\left(a+\dfrac{k(b-a)}{n}\right)$$
Autre méthode
Sur $[x_{k}\;,\ x_{k+1}]\;,\ f$ est croissante alors, $f(x_{k})\leq f(x)\leq f(x_{k+1})$ et donc \begin{eqnarray} \int_{x_{k}}^{x_{k+1}}f(x_{k})\mathrm{d}x&\leq&\int_{x_{k}}^{x_{k+1}}f(x)\mathrm{d}x\;\leq\;\int_{x_{k}}^{x_{k+1}}f(x_{k+1})\mathrm{d}x\nonumber \\ \\ f(x_{k})(x_{k+1}-x_{k})&\leq&\int_{x_{k}}^{x_{k+1}}f(x)\mathrm{d}x\;\leq\; f(x_{k+1})(x_{k+1}-x_{k})\nonumber \\ \\ \dfrac{b-a}{n}f\left(a+\dfrac{k(b-a)}{n}\right)&\leq&\int_{x_{k}}^{x_{k+1}}f(x)\mathrm{d}x\;\leq\;\dfrac{b-a}{n}f\left(a+\dfrac{(k+1)(b-a)}{n}\right)\nonumber \\ \\ \dfrac{b-a}{n}\sum_{k=0}^{n-1}f\left(a+\dfrac{k(b-a)}{n}\right)&\leq&\sum_{k=0}^{n-1}\int_{x_{k}}^{x_{k+1}}f(x)\mathrm{d}x\;\leq\;\dfrac{b-a}{n}\sum_{k=0}^{n-1}f\left(a+\dfrac{(k+1)(b-a)}{n}\right)\nonumber \\ \\ \dfrac{b-a}{n}\sum_{k=0}^{n-1}f\left(a+\dfrac{k(b-a)}{n}\right)&\leq&\int_{a}^{b}f(x)\mathrm{d}x\;\leq\;\dfrac{b-a}{n}\sum_{k=1}^{n}f\left(a+\dfrac{k(b-a)}{n}\right)\nonumber \end{eqnarray}
Ainsi, $$s_{n}\leq\int_{a}^{b}f(x)\mathrm{d}x\leq\mathcal{S}_{n}$$
$\dfrac{\mathcal{S}_{n}+s_{n}}{2}$ est une valeur approchée de $\int_{a}^{b}f(x)\mathrm{d}x$ à $\dfrac{\mathcal{S}_{n}-s_{n}}{2}$ près.
$\dfrac{\mathcal{S}_{n}-s_{n}}{2}=(f(b)-f(a))\left(\dfrac{b-a}{n}\right)$
Donc en subdivisant de plus en plus finement l'intervalle $[a\;,\ b]$, les suites $s_{n}$ et $\mathcal{S}_{n}$ convergent vers un même nombre, ce nombre est l'aire sous la courbe $C_{f}.$
$$\lim_{n\rightarrow+\infty}s_{n}=\lim_{n\rightarrow+\infty}\mathcal{S}_{n}=\int_{a}^{b}f(x)\mathrm{d}x$$
V Fonction définie par une intégrale
$\centerdot\ \ $ Soit $I$ un intervalle de $\mathbb{r}$ et $a\;,\ b\in\mathbb{R}$, l'intégrale $\int_{a}^{b}f(x)\mathrm{d}x$ existe si $f$ est continue sur $[a\;,\ b].$
$\centerdot\ \ $ Soit $f$ une fonction continue sur $I$, pour tous $a\;,\ x\in I$ la fonction $F$ définie par $$F(x)=\int_{a}^{x}f(t)\mathrm{d}t$$ est une fonction définie par une intégrale.
$\centerdot\ \ f$ est continue sur $I$, alors $f$ admet une primitive $G$ sur $I$, donc $F(x)=[G(t)]_{x}^{a}=G(x)-G(a).$ Ainsi, $F'(x)=G'(x)=f(x)$
Exemple
Soit $F$ la fonction définie par $$F(x)=\int_{0}^{x}\dfrac{1}{\sqrt{1+t^{2}}}\mathrm{d}t$$
On a $\dfrac{1}{\sqrt{1+t^{2}}}$ continue sur $\mathbb{R}$, donc $F$ est définie sur $\mathbb{R}$ et $$\forall\;-x\in\mathbb{R}\;,\ F(-x)=\int_{0}^{-x}\dfrac{1}{\sqrt{1+t^{2}}}\mathrm{d}t=-\int_{0}^{x}\dfrac{1}{\sqrt{1+u^{2}}}\mathrm{d}u=-F(x)$$ après changement de variables $u=-t\ \Rightarrow\ \mathrm{d}u=-\mathrm{d}t$, donc $F$ est impaire.
$\dfrac{1}{\sqrt{1+t^{2}}}$ est continue sur $\mathbb{R}$, donc admet une primitive $F_{1}$ et donc
$F(x)=F_{1}(x)-F_{1}(0)\ \Rightarrow\ F'(x)=F'_{1}(x)=\dfrac{1}{\sqrt{1+x^{2}}}>0$, donc $F$ est strictement croissante. On a :
\begin{eqnarray}1+t^{2}\geq t^{2}&\Rightarrow&\dfrac{1}{\sqrt{1+t^{2}}}\leq\dfrac{1}{t^{2}}\nonumber \\ \\&\Rightarrow&0\leq\int_{0}^{x}\dfrac{1}{\sqrt{1+t^{2}}}\mathrm{d}t\leq\int_{0}^{x}\dfrac{1}{t^{2}}\mathrm{d}t\nonumber \\ \\&\Rightarrow&0\leq F(x)\leq\left[-\dfrac{1}{t}\right]_{0}^{x}\nonumber \\ \\&\Rightarrow&0\leq F(x)\leq -\dfrac{1}{x}+1\nonumber \end{eqnarray}
Ainsi, $$0\leq\lim_{x\rightarrow+\infty}F(x)\leq 1$$
$\centerdot\ \ f$ continue sur $\mathbb{R}\;,\ u(x)$ et $v(x)$ dérivable sur $\mathbb{R}$, alors
$$F(x)=\int_{u(x)}^{v(x)}f(t)\mathrm{d}t$$ existe si, et seulement, $u(x)$ et $v(x)$ existent et appartiennent au domaine de continuité de $f.$
$f$ continue sur $\mathbb{R}$ donc admet une primitive $F_{1}$, alors $$F(x)=[F_{1}(t)]_{u(x)}^{v(x)}=F_{1}(v(x))-F_{1}(u(x))$$
$F_{1}$ dérivable sur $\mathbb{R}$, alors $F_{1}(u(x))$ est dérivable sur $\mathbb{R}$, idem pour $F_{1}(v(x))$, d'où $F$ dérivable sur $\mathbb{R}.$
Donc \begin{eqnarray} F'(x)&=&v'(x)F'_{1}(v(x))-u'(x)F'_{1}(u(x))\nonumber \\ \\&=&v'(x)f(v)-u'(x)f(u)\nonumber \end{eqnarray}
VI Calcul d'aire et de volume
VI.1 Calcul d'aires
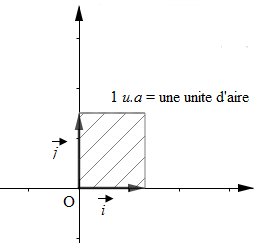
Soit $(O\;;\ \vec{i}\;,\ \vec{j})$ un repère orthogonal, $||\vec{i}||=m\;cm\;,\ ||\vec{j}||=n\;cm.$
L'unité d'aire est l'aire du quadrilatère construit sur les vecteurs de bases du repères. $$1\text{ unité d'aire }(u.a)=m\times n\;cm^{2}$$
$\centerdot\ \ $ Soit $f\geq 0$ sur $[a\;,\ b]$.
L'aire $\mathcal{A}$ de la partie du plan comprise entre $C_{f}$, l'axe des abscisses et les droites d'équation $x=a$ et $x=b$ est égale à : $$\mathcal{A}=\int_{a}^{b}f(x)\mathrm{d}x\;u.a$$
Exemple
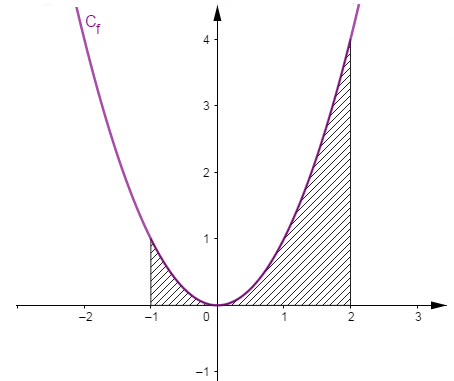
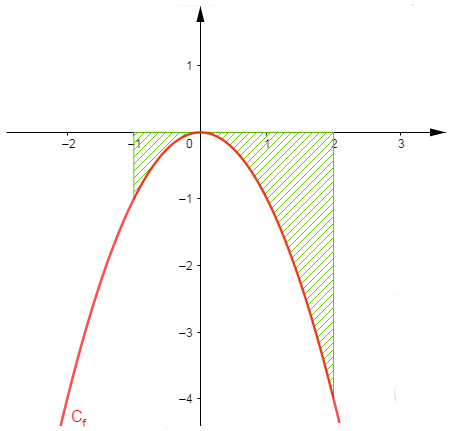
Soit $(O\;;\ \vec{i}\;,\ \vec{j})$ un repère orthogonal, $||\vec{i}||=||\vec{j}||=1\;cm.$ On considère la parabole $C_{f}$ représentant la fonction $f$ définie sur $\mathbb{R}$ par $f(x)=x^{2}.$
Calculer l'aire $\mathcal{A}$ en $cm^{2}$ du domaine délimité par $C_{f}$, l'axe des abscisses et les droites d'équation $x=-1$ et $x=2$
Résolution
On a $1\;u.a=1\;cm^{2}$
\begin{eqnarray} \mathcal{A}&=&\int_{-1}^{2}f(x)\mathrm{d}x\nonumber \\ \\&=&\int_{-1}^{2}x^{2}\mathrm{d}x\nonumber \\ \\&=&\left[\dfrac{x^{3}}{3}\right]_{-1}^{2}\nonumber \\ \\&=&\dfrac{8}{3}+\dfrac{1}{3}\nonumber \\ \\&=&3\;cm^{2}\nonumber \end{eqnarray}
$\centerdot\ \ $ Soit $f\geq 0$ sur $[a\;,\ b]$.
L'aire de la partie du plan comprise entre $C_{f}$, l'axe des abscisses et les droites d'équation $x=a$ et $x=b$ est égale à : $$\int_{a}^{b}-f(x)\mathrm{d}x\;u.a$$
Exemple
Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x)=-x^{2}.$
Calculer l'aire $\mathcal{A}$ du domaine délimité par $C_{f}$, l'axe des abscisses et les droites d'équation $x=-1$ et $x=2$
Résolution
\begin{eqnarray} \mathcal{A}&=&\int_{-1}^{2}-f(x)\mathrm{d}x\nonumber \\ \\&=&\int_{-1}^{2}x^{2}\mathrm{d}x\nonumber \\ \\&=&\left[\dfrac{x^{3}}{3}\right]_{-1}^{2}\nonumber \\ \\&=&\dfrac{8}{3}+\dfrac{1}{3}\nonumber \\ \\&=&3\;cm^{2}\nonumber \end{eqnarray}
$\centerdot\ \ $ Soit $f$ et $g$ deux fonctions continues sur $[a\;,\ b].$
L'aire de la partie du plan comprise entre $C_{f}\;,\ C_{g}$ et les droites d'équation $x=a$ et $x=b$ est égale à : $$\int_{a}^{b}|f(x)-g(x)|\mathrm{d}x\;u.a$$
Exemple : cas particulier d'une fonction changeant de signe
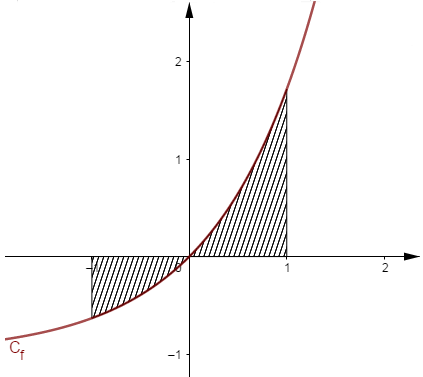
Soit $f$ et $g$ les fonctions définies sur $\mathbb{R}$ par $f(x)=\mathrm{e}^{x}-1$ et $g(x)=0$
Calculer l'aire $\mathcal{A}$ du domaine délimité par $C_{f}\;,\ C_{g}$ et les droites d'équation $x=-1$ et $x=1$
Résolution
\begin{eqnarray} \mathcal{A}&=&\int_{-1}^{1}|f(x)-g(x)|\mathrm{d}x\nonumber \\ \\&=&\int_{-1}^{1}|\mathrm{e}^{x}-1|\mathrm{d}x\nonumber \\ \\&=&\int_{-1}^{0}-(\mathrm{e}^{x}-1)\mathrm{d}x+\int_{0}^{1}\mathrm{e}^{x}-1\mathrm{d}x\nonumber \\ \\&=&-[\mathrm{e}^{x}-x]_{-1}^{0}+[\mathrm{e}^{x}-x]_{0}^{1}\nonumber \\ \\&=&-\left[1-\dfrac{1}{\mathrm{e}}-1\right]+[\mathrm{e}-1-1]\nonumber \\ \\&=&\dfrac{1}{\mathrm{e}}+\mathrm{e}-2\nonumber \end{eqnarray}
$\centerdot\ \ $ Soit $f$ une fonction continue sur $[a\;,\ b]$ et $D$ une droite d'équation $\alpha x+\beta.$
L'aire de la partie du plan comprise entre $C_{f}\;,\ D$ et les droites d'équation $x=a$ et $x=b$ est égale à : $$\int_{a}^{b}|f(x)-(\alpha x+\beta)|\mathrm{d}x\;u.a$$
Exemple
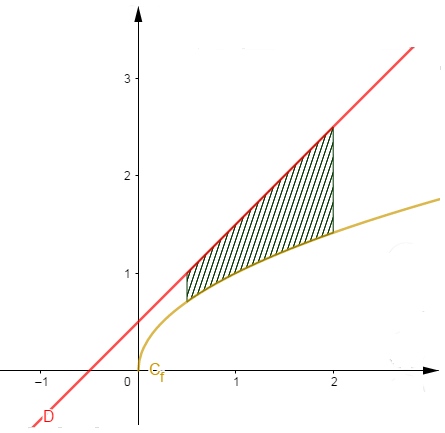
Soit $f$ la fonction définie sur $\mathbb{R}_{+}$ par $f(x)=\sqrt{x}$ et $D\ :\ x+\dfrac{1}{2}$
Calculer l'aire $\mathcal{A}$ du domaine délimité par $C_{f}\;,\ D$ et les droites d'équation $x=\dfrac{1}{2}$ et $x=2$
\begin{eqnarray} \mathcal{A}&=&\int_{1/2}^{2}|f(x)-(\alpha x+\beta)|\mathrm{d}x\nonumber \\ \\&=&\int_{1/2}^{2}(x+\dfrac{1}{2}-\sqrt{x})\mathrm{d}x\nonumber \\ \\&=&\left[\dfrac{x^{2}}{2}+\dfrac{1}{2}x-\dfrac{x^{3/2}}{\dfrac{3}{2}}\right]_{1/2}^{2}\nonumber \\ \\&=&\left(2+1-\dfrac{4\sqrt{2}}{3}\right)-\left(\dfrac{1}{8}+\dfrac{1}{4}-\dfrac{\sqrt{2}}{6}\right)\nonumber \\ \\&=&3-\dfrac{3}{8}-\dfrac{7\sqrt{2}}{6}\nonumber \end{eqnarray}
VI.2 Calcul de volume
Soit $(O\;;\ \vec{i}\;,\ \vec{j}\;,\ \vec{k})$ un repère orthogonal.
L'unité de volume est le volume du parallélépipède construit sur les vecteurs de bases du repères.
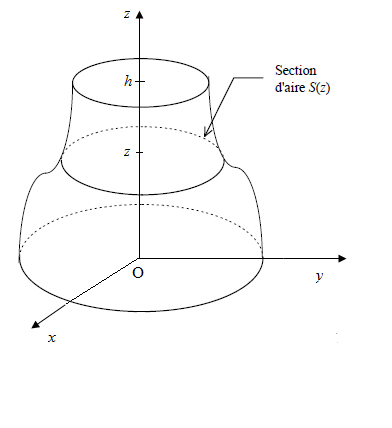
Soit $S$ un solide de hauteur $h$. Un plan $\mathcal{P}$ parallèle au plan $(x'Ox)$ coupe $S$ suivant une figure plane de surface $S(z).$ Le volume $\mathcal{V}$ de $S$ est égal à $$\mathcal{V}=\int_{0}^{h}S(z)\mathrm{d}z\;u.v$$
$1\;u.v=\text{une unité de volume}$
Exemples
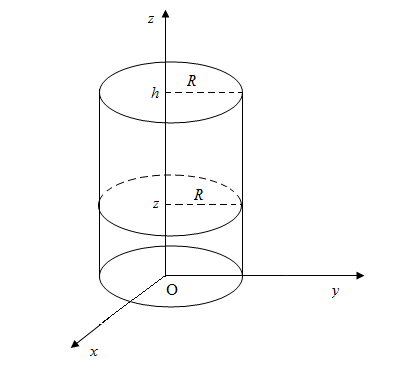
a) Cylindre $(R\;,\ h)$
$S(z)=\pi R^{2}$ \begin{eqnarray} \mathcal{V}&=&\int_{0}^{h}S(z)\mathrm{d}z\nonumber \\ \\&=&\int_{0}^{h}\pi R^{2}\mathrm{d}z\nonumber \\ \\&=&[\pi R^{2}]_{0}^{h}\nonumber \\ \\&=&\pi R^{2}h\nonumber \end{eqnarray}
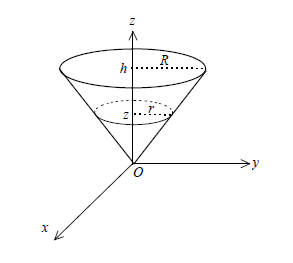
b) Cône $(R\;,\ h)$
$S(z)=\pi r^{2}$, d'après Thalès $\dfrac{r}{R}=\dfrac{z}{h}$, donc $S(z)=\pi\dfrac{R^{2}}{h^{2}}z^{2}.$
Donc \begin{eqnarray} \mathcal{V}&=&\int_{0}^{h}S(z)\mathrm{d}z\nonumber \\ \\&=&\int_{0}^{h}\pi\dfrac{R^{2}}{h^{2}}z^{2}\mathrm{d}z\nonumber \\ \\&=&\pi\dfrac{R^{2}}{h^{2}}\int_{0}^{h}z^{2}\mathrm{d}z\nonumber \\ \\&=&\pi\dfrac{R^{2}}{h^{2}}\left[\dfrac{z^{3}}{3}\right]_{0}^{h}\nonumber \\ \\&=&\pi\dfrac{R^{2}h}{3}\nonumber \end{eqnarray}
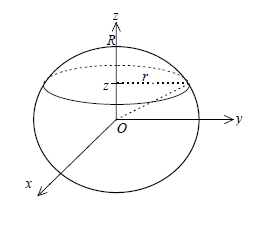
c) Sphère de rayon $R$
$S(z)=\pi r^{2}$ or $r^{2}+z^{2}=R^{2}\ \Rightarrow\ r^{2}=R^{2}-z^{2}$, donc $S(z)=\pi(R^{2}-z^{2}).$
Alors \begin{eqnarray} \mathcal{V}&=&\int_{-R}^{R}S(z)\mathrm{d}z\nonumber \\ \\&=&\int_{-R}^{R}\pi(R^{2}-z^{2})\mathrm{d}z\nonumber \\ \\&=&2\pi\int_{0}^{R}(R^{2}-z^{2})\mathrm{d}z\nonumber \\ \\&=&2\pi\left[R^{2}z-\dfrac{z^{3}}{3}\right]_{0}^{R}\nonumber \\ \\&=&2\pi\left(R^{3}-\dfrac{R^{3}}{3}\right)\nonumber \\ \\&=&\dfrac{4}{3}\pi R^{3}\nonumber \end{eqnarray}
Remarque
Soit $f$ une fonction continue sur $[a\;,\ b]$, alors le volume engendré par la rotation de $C_{f}\;,\ x=a$ et $x=b$ autour de l'axe des abscisses est égal à $$\mathcal{V}=\int_{a}^{b}\pi(f(x))^{2}\mathrm{d}x$$

Commentaires
Anonyme (non vérifié)
sam, 07/27/2019 - 13:51
Permalien
Merci à vous pour tout ce que
M Pouye (non vérifié)
lun, 01/11/2021 - 07:22
Permalien
C'est très intéressant, merci
Anonyme (non vérifié)
lun, 04/17/2023 - 18:20
Permalien
ghferuipguitg-ioiuug tefg"o
Ajouter un commentaire