EXERCICE 1  5 points

Cet exercice est un questionnaire à choix multiples (QCM). Pour chacune des questions suivantes, une seule des trois réponses est exacte. Aucune justification n'est demandée. Une bonne réponse rapporte un point, une mauvaise réponse, une réponse multiple ou l'absence de réponse à une question ne rapporte ni n'enlève de point. Indique sur ta copie le numéro de la question et la réponse correspondante.

		Réponses
N°	Questions	A	B	C
1	On considère la série statistique dont les modalités sont : $12$ ; $14$ ; $13$ ; $14$ ; $x$. La moyenne de cette série vaut $12$. La valeur de la modalité $x$ est égale à :	$12$	$7$	$13$
2	Un sac contient $5$ boules rouges, $3$ boules noires et $2$ jaunes, toutes identiques et indiscernables au toucher. La probabilité de tirer une boule jaune est égale à :	$\dfrac{2}{8}$	$\dfrac{1}{2}$	$\dfrac{1}{5}$
3	Le nombre de diviseurs entiers naturels de $7^2$ est :	$4$	$7$	$3$
4	On considère la figure ci-contre. On donne $Mes(\widehat{CAB}) = 37°$. $Mes(\widehat{DOF})$ est égal à :	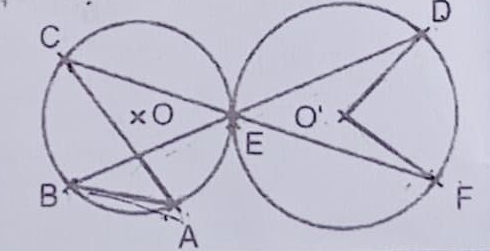$74°$	$18,50°$	$37°$
5	On considère les intervalles $I = ]−∞ ; 3]$ et $J = [−2 ; 0[$. L’intersection de $I$ et $J$ est représentée par :	$−2 ≤ x ≤ 0$	$−2 ≤ x < −3$	$−3 ≤ x < −2$

EXERCICE 2  5 points

Les questions 1 et 2 sont indépendantes. Pour chacune des questions ci-dessous, on fera apparaître les différentes étapes de calcul.

On donne : $A = \dfrac{5}{4} - \dfrac{1}{4} \times \dfrac{5}{2}$ et $B = 4x^2 - 12x + 9 - (x + 3)(2x - 3)$.

1. Calcule $A$, puis écris le résultat en notation scientifique.

2. a) Développe, réduis et ordonne $B$ suivant les puissances décroissantes de $x$.

     b) Factorise $B$ sous la forme d'un produit de facteurs du premier degré.

     c) Résous dans $\mathbb{R}$ l'équation : $(x - 6)(2x - 3) = 0$.

     d) Calcule la valeur numérique de $B$ pour $x = \sqrt{3}$.

     e) Donne un encadrement à $10^{-1}$ près de $E = 24 - 15\sqrt{3}$ sachant que $1,732 \leq \sqrt{3} \leq 1,733$.

     f) En déduis une écriture simplifiée de $|24 - 15\sqrt{3}|$.

EXERCICE 3  5 points

Soit $(O,\vec{i},\vec{j})$ un repère orthonormé. L'unité de longueur est le centimètre. On donne les points : $A(-2;-4)$, $B(-4;0)$ et $C(2;3)$.

1. a) Place les points $A$, $B$ et $C$ dans le repère.

$\textit{La figure sera complétée au fur et à mesure.}$

     b) Calcule les coordonnées des vecteurs $\overrightarrow{AB}$ et $\overrightarrow{BC}$, puis montre que les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{BC}$ sont orthogonaux.

2.a) Où se situe le centre d'un cercle circonscrit à un triangle rectangle ?

    b) Vérifie que le point $K$ milieu du segment $[AC]$ a pour coordonnées $(0;-\dfrac{1}{2})$.

     c) Place le point $K$, puis construis le cercle $(\mathcal{C})$ circonscrit au triangle rectangle $ABC$.

3.a) Construis le point $E$ image du point $B$ par la symétrie centrale de centre $K$.

   b) Calcule les coordonnées du point $E$.

    c) Justifie que le quadrilatère $ABCE$ est un rectangle.

4. a) Démontre qu'une équation cartésienne de la droite $(D)$ perpendiculaire à $(AC)$ et passant par le point $K$ est : $8x + 14y + 7 = 0$.

    b) Comment appelle-t-on la droite $(D)$ relativement au cercle $(\mathcal{C})$ ?

EXERCICE 4  5 points

L'unité de longueur est le mètre.

Pour son approvisionnement en eau potable dans un quartier de Libreville, Monsieur Ndong a construit un château d'eau (figure1). Ce château est constitué d'un cylindre de révolution accolé à un tronc de cône réalisé à partir de la section d'un cône par un plan parallèle à sa base (figure 2).

On donne : $S0 = 6,4$ ; $SB = 8$ et $SI = 3,6$.

1. a) À partir de la figure 2, montre que : $OB = 4,8$.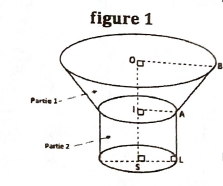

   b) Calcule le volume exact $V_c$ du cône de sommet $S$ et de base le disque de centre $O$.

2. Calcule la distance $AI$.

3. a) Calcule le quotient $\dfrac{SI}{SO}$ sous la forme d'une fraction irréductible.

    b) Que représente ce nombre ?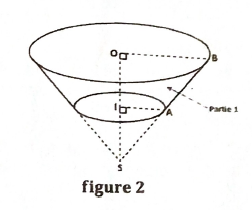

4. Soit $V_T$ le volume du tronc de cône. Montre que $V_T = 40,404\pi$.

5. En déduis la valeur exacte du volume total $V$ du château d'eau.

6. Calcule $\tan \widehat{OSB}$, puis en déduis la mesure de l'angle $\widehat{OSB}$ arrondie au degré près.

Correction du BEPC