Application linéaire - 4e
Classe:
Quatrième
I. Définition
Soit $a$ un nombre rationnel. On appelle application linéaire toute correspondance qui à tout nombre rationnel $x$ associe le nombre rationnel $a\times x.$
Si on note par $f$ l'application linéaire alors :
$\centerdot\ \ f(x)$ ("lire $f$ de $x$") est l'image de $x$ par l'application linéaire $f.$
On écrit alors :
$$f(x)=ax$$
$\centerdot\ \ a$ est appelé le coefficient de l'application linéaire.
$\centerdot\ \ x$ est l'antécédent de $f(x)$ par l'application linéaire $f.$
Exemple :
$$f(x)=4x\;,\quad g(x)=\dfrac{2}{3}x\quad\text{et}\quad A(x)=-x$$
sont toutes des applications linéaires de coefficients respectifs $4\;,\ \dfrac{2}{3}\;,\ $ et $\ -1$
On a :
$f(0)=4\times 0=0.$
Ainsi, $0$ est l'image de $0$ par $f$
$0$ est l'antécédent de $0$ par $f$
$f(-4)=4\times(-4)=-16.$
Donc, $-16$ est l'image de $-4$ par $f$
$-4$ est l'antécédent de $-16$ par $f$
Application 1
1) Quelle est l'image de $\dfrac{3}{2}$ par $g\ ?$
2) Quel est l'antécédent de $-5$ par $g\ ?$
Solution
1) Soit $g(x)=\dfrac{2}{3}x$
Alors, $g\left(\dfrac{3}{2}\right)=\dfrac{2}{3}\times\dfrac{3}{2}=1$
Ainsi, l'image de $\dfrac{3}{2}$ par $g$ est $1.$
2) $g(x)=-5$ donc, $\dfrac{2}{3}x=-5$
Ce qui entraine :
$\begin{array}{rcl} x&=&\dfrac{-5}{\dfrac{2}{3}}\\ \\&=&\dfrac{-5}{1}\times\dfrac{3}{2}\\ \\&=&\dfrac{-15}{2}\end{array}$
D'où, l'antécédent de $-5$ par $g$ est $\dfrac{-15}{2}$
Application 2
Soit $A(x)=\dfrac{-1}{3}x$ une application linéaire.
1) Calculer l'image de : $0\;,\ -1\;,\ \dfrac{-1}{2}$
2) Déterminer les nombres rationnels $x$ tels que leurs images par $A$ sont : $\dfrac{5}{3}\;,\ -12\ $ et $\ 0$
Solution
1) Calculons l'image de $0\;,\ $ de $\ -1\;,\ $ et de $\ \dfrac{-1}{2}$
$A(0)=\dfrac{-1}{3}\times 0=0$ donc, l'image de $0$ par $A$ est $0$
$A(-1)=\dfrac{-1}{3}\times(-1)=\dfrac{1}{3}$ donc, l'image de $-1$ par $A$ est $\dfrac{1}{3}$
$A\left(\dfrac{-1}{2}\right)=\dfrac{-1}{3}\times\dfrac{-1}{2}=\dfrac{1}{6}$ donc, $\dfrac{1}{6}$ est l'image de $\dfrac{-1}{2}$ par $A$
2) Déterminons les antécédents par $A$ des nombres rationnels $\dfrac{5}{3}\;,\ -12\ $ et $\ 0$
$A(x)=\dfrac{5}{3}$ donc, $\dfrac{-1}{3}x=\dfrac{5}{3}$
Par suite :
$\begin{array}{rcl} x&=&\dfrac{\dfrac{5}{3}}{\dfrac{-1}{3}}\\ \\&=&\dfrac{5}{3}\times\dfrac{3}{-1}\\ \\&=&\dfrac{-15}{3}\\ \\&=&-5\end{array}$
D'où, $x=-5$
Ainsi, $-5$ est l'antécédent de $\dfrac{5}{3}$ par $A$
Soit $A(x)=-12$ alors, $\dfrac{-1}{3}x=-12$
Donc,
$\begin{array}{rcl} x&=&\dfrac{-12}{\dfrac{-1}{3}}\\ \\&=&\dfrac{-12}{1}\times\dfrac{3}{-1}\\ \\&=&36\end{array}$
Ainsi, $x=36$
D'où, $36$ est l'antécédent de $-12$ par $A$
Soit $A(x)=0$ alors, $\dfrac{-1}{3}x=0$
Ce qui donne $x=0$
Par suite, l'antécédent de $0$ par $A$ est $0$
Remarque
Toute situation de proportionnalité est une application linéaire et inversement.
Exemple
Considérons un véhicule roulant à une vitesse de $60\;km/h.$
La distance $d$ parcourue et le temps mis sont deux grandeurs proportionnelles.
On écrit : $d=60t$ qui est une application linéaire de coefficient $60.$
II. Propriétés des applications linéaires
Soit $f$ une application linéaire.
Quels que soient les nombres rationnels $u\;,\ v\ $ et $\ w$, on a :
$\centerdot\ f(u+v)=f(u)+f(v)$
$\centerdot\ f(kw)=kf(w)\;,\quad k$ un nombre.
Exemple
On considère l'application linéaire $f(x)=\dfrac{4}{3}x$
1) Calculer $f(5)\ $ et $\ f(2)$
2) Calculer de deux manières différentes $f(7)\ $ et $\ f(12)$
Solution
1) $f(5)=\dfrac{4}{3}\times 5=\dfrac{20}{3}$
$f(2)=\dfrac{4}{3}\times 2=\dfrac{8}{3}$
2) 1er méthode
$f(7)=\dfrac{4}{3}\times 7=\dfrac{28}{3}$
$f(12)=\dfrac{4}{3}\times 12=16$
2èm méthode
$\begin{array}{rcl} f(7)&=&f(5+2)\\ \\&=&f(5)+f(2)\\ \\&=&\dfrac{20}{3}+\dfrac{8}{3}\\ \\&=&\dfrac{28}{3}\end{array}$
Donc, $f(7)=\dfrac{28}{3}$
$\begin{array}{rcl} f(12)&=&f(6\times 2)\\ \\&=&6\times f(2)\\ \\&=&6\times\dfrac{8}{3}\\ \\&=&\dfrac{48}{3}\\ \\&=&16\end{array}$
Ainsi, $f(12)=16$
III. Représentation graphique d'une application linéaire
Un repère est un ensemble de deux axes perpendiculaires en un point souvent noté $O$ et appelé l'origine du repère.
Ainsi, la représentation graphique d'une application linéaire est une droite qui passe par $O$ et par le point $A\begin{pmatrix} 1\\a\end{pmatrix}$ avec $a$ le coefficient de l'application linéaire.
Exemple
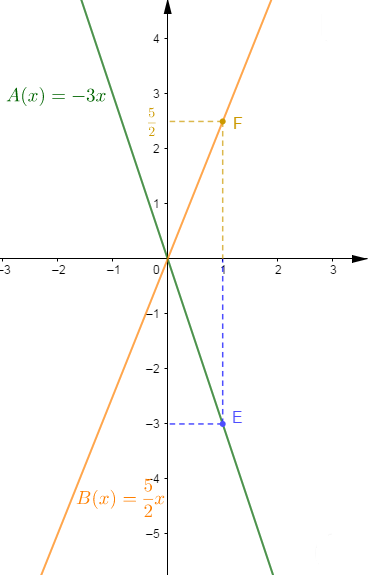
Représenter les applications linéaires $A(x)=-3x\ $ et $\ B(x)=\dfrac{5}{2}x$
Solution
Pour l'application linéaire $A$, on trace la droite passant par $O$ et par le point $E\begin{pmatrix} 1\\-3\end{pmatrix}$
Donc, on place le point $E$ dans un repère et on trace la droite qui passe par $O\ $ et $\ E$
Pour l'application linéaire $B$, on trace la droite passant par $O$ et par le point $F\begin{pmatrix} 1\\ \\\dfrac{5}{2}\end{pmatrix}$
De la même manière, on place le point $F$ dans le même repère et on trace la droite passant par $O\ $ et $\ F$
Auteur:
Mamadou Siradji Dia

Commentaires
Anonyme (non vérifié)
dim, 06/06/2021 - 20:10
Permalien
Déterminer l'aplication
Anonyme (non vérifié)
dim, 06/06/2021 - 20:10
Permalien
Déterminer l'aplication
Ousmane diouf (non vérifié)
dim, 04/30/2023 - 17:19
Permalien
Super
Ousmane diouf (non vérifié)
dim, 04/30/2023 - 17:19
Permalien
Super
Mbongo (non vérifié)
mar, 12/12/2023 - 21:04
Permalien
Cenprendre les maths
Mbongo (non vérifié)
mar, 12/12/2023 - 21:04
Permalien
Cenprendre les maths
Ajouter un commentaire