Étude de fonctions - 1er S

Soit $f$ une fonction dérivable sur un intervalle ouvert $I$ et soit $a$ un élément de $I$ et $A(a\;,\ f(a))$ un point de $\mathcal{C_{f}}.$ 

 

Si la courbe $\mathcal{C_{f}}$ traverse sa tangente au point $A$ alors $A$ est un point d'inflexion de $\mathcal{C_{f}}.$

Soit $f$ une fonction dérivable sur un intervalle ouvert $I.$ 

 

Si au point $a$ de $I$ $f'(x)$ s'annule en changeant de signe, alors le point $A(a\;,\ f(a))$ est un point d'inflexion de la courbe $\mathcal{C_{f}}.$

 

Nous verrons une autre condition suffisante

 

La réciproque du théorème est fausse.

1) Détermination des ensembles de définition, de continuité et, si possible de dérivabilité

 

2) Étude des propriétés de la fonction : parité, périodicité. 

 

En déduire les propriétés éventuelles de la courbe représentative. 

 

Choisir le domaine d'étude.

 

3) Calcul des limites aux bornes du domaine d'étude ; détermination des branches infinies, des asymptotes éventuelles.

 

4) Calcul de la dérivée, après avoir déterminé le domaine de dérivabilité.

5) Tableau de variation de la fonction

 

6) Tracé de la courbe représentative. 

 

Préciser, si possible, les points particuliers (inflexion, anguleux, etc ...) et les tangentes en ces points.

 

L'ordre n'est pas obligatoire

1) $f(x)=x^{2}-2x-3$

 

$\mathcal{D_{f}}=\mathbb{R}$

 

$f$ n'est ni paire ni impaire, on va donc l'étudier sur $\mathbb{R}$

 

$\lim_{x\rightarrow +\infty}f(x)=\lim_{x\rightarrow +\infty}f(x)=+\infty$

 

la courbe présente donc deux branches infinies

 

$\lim_{x\rightarrow +\infty}\dfrac{f(x)}{x}=+\infty\text{ et }\lim_{x\rightarrow -\infty}\dfrac{f(x)}{x}=-\infty$

 

La courbe présente donc deux branches paraboliques de direction l'axe des ordonnées.

 

$F$ est dérivable sur $\mathbb{R}$ comme fonction polynôme et pour tout $x$ réel $f'(x)=2x-2.$

 

L'étude du signe de cette dérivée est simple et nous avons le tableau de variation suivant :

Il serait utile pour tracer la courbe de $f$ d'avoir quelques points. 

 

Nous voyons que $f(1)=-4$ mais un seul point ne saurait suffire.

 

Remplissons le tableau suivant et utilisons les points ainsi obtenus.

 

$$\begin{array}{|c|c|c|c|c|c|c|c|} \hline x&-2&-1&0&2&3&4&5\\ \hline f(x)&5&0&-3&-3&0&5&12\\ \hline \end{array}$$

 

D'où la courbe suivante

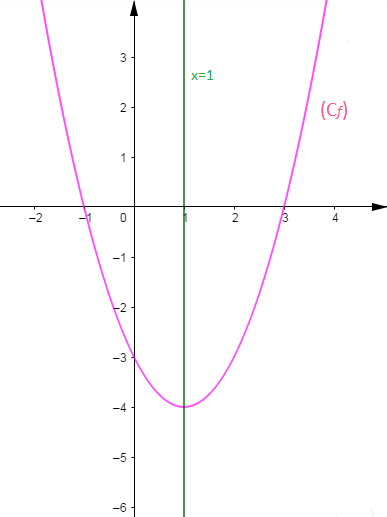
Le tableau des valeurs et la courbe montre qu'il y'a un axe de symétrie qui est la droite d'équation $x=1.$

 

Vous le montrerez aisément.

 

Nous constatons aussi que la courbe coupa l'axe des abscisses en deux points. 

 

Pour avoir l'abscisse de ces deux points, il faut résoudre l'équation $f(x)=0$ (si possible).

 

$f(0)$ donne l'ordonnée du point d'intersection de la courbe avec l'axe des ordonnées.

 

La courbe obtenue est une parabole vue en principe en classe de seconde.

 

2) $f(x)=x^{3}-3x^{2}\;,\quad f'(x)=3x^{2}-6x$

 

Le signe de la dérivée ne pose aucun problème et nous avons le tableau de variations suivant :

 

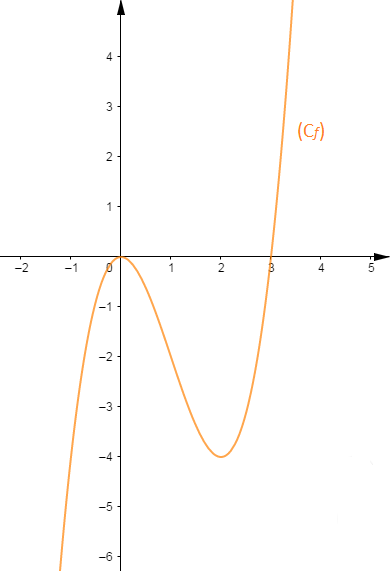
La courbe de cette fonction a été dessinée pour illustrer la notion de point d'inflexion.

 

$f''(x)=6x-6.$ 

 

Cette dérivée seconde s'annule pour $x=1$ et change de signe.

 

On retrouve une condition suffisante pour l'existence du point d'inflexion.

3) $f(x)=\dfrac{2x+3}{x-1}$ une telle fonction est appelée fonction homographique.

 

Elle est définie sur $\mathbb{R}\setminus\{1\}=]-\infty\;;\ 1[\cup]1\;;\ +\infty[.$ 

 

Le domaine de définition n'est pas symétrique par rapport à $0$ donc la fonction n'est ni paire ni impaire. 

 

Nous avons donc $4$ limites à calculer

 

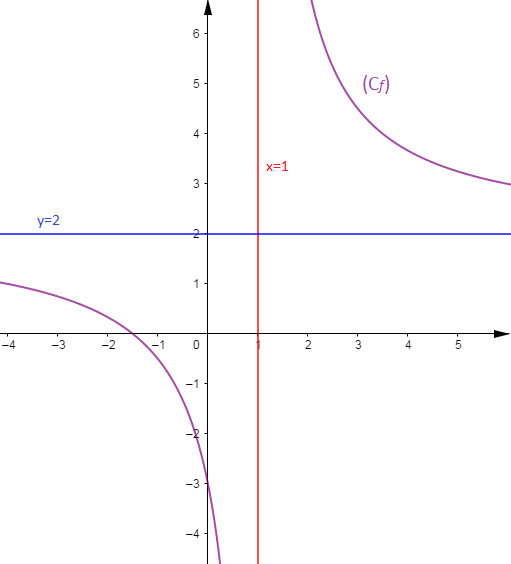
$\lim_{x\rightarrow +\infty}f(x)=\lim_{x\rightarrow -\infty}f(x)=2$ donc la droite d'équation $y=2$ est asymptote horizontale pour la courbe

 

$\lim_{x\rightarrow 1^{-}}f(x)=-\infty\text{ et }\lim_{x\rightarrow 1^{+}}f(x)=+\infty$ donc la droite d'équation $x=1$ est asymptote verticale pour la courbe

 

$f$ est dérivable sur son domaine de définition comme fonction rationnelle et pour tout $x$ différent de $1$ $f'(x)=\dfrac{-5}{(x-1)^{2}}$ nous voyons aisément que cette dérivée est toujours négative et la fonction est strictement décroissante dans chaque intervalle où elle est définie d'où le tableau de variation suivant :

Pour la courbe il convient de faire comme sur le $1^{er}$ exemple : 

 

Chercher des points en particulier (lorsqu'ils existent) les intersections de la courbe avec les axes.

4) $f(x)=2x-1+\dfrac{2}{x-3}$

 

$f$ est défini sur $\mathbb{R}\setminus\{3\}$ est continue et dérivable sur son domaine de définition car c'est une fonction rationnelle.

 

$f$ n'est ni paire ni impaire car son domaine de définition n'est pas symétrique par rapport à $0.$

 

D'où le domaine d'étude est le domaine de définition.

 

$\lim_{x\rightarrow -\infty}f(x)=-\infty\ $ car $\ \lim_{x\rightarrow -\infty}(2x-1)\ $ et $\ \lim_{x\rightarrow -\infty}\dfrac{2}{x-3}=0$

 

$\lim_{x\rightarrow +\infty}f(x)=+\infty\ $ car $\ \lim_{x\rightarrow +\infty}(2x-1)=+\infty\ $ et $\ \lim_{x\rightarrow +\infty}\dfrac{2}{x-3}=0$

 

$\lim_{x\rightarrow 3^{-}}\dfrac{2}{x-3}=-\infty\ $ car $\ \lim_{x\rightarrow 3^{-}}(x-3)=0^{-}\ $ donc, $\ \lim_{x\rightarrow 3^{-}}f(x)=-\infty$

 

$\lim_{x\rightarrow 3^{+}}\dfrac{2}{x-3}=+\infty\ $ car $\ \lim_{x\rightarrow 3^{+}}(x-3)=0^{+}\ $ donc, $\ \lim_{x\rightarrow 3^{+}}=+\infty$

 

La droite d'équation $x=3$ est asymptote verticale à la courbe de $f.$

 

Nous sommes en présence de deux branches infinies mais l'écriture de $f(x)$ suggère l'équation de l'asymptote oblique.

 

En effet $\lim_{x\rightarrow +\infty}\left(f(x)-(2x-1)\right)=\lim_{x\rightarrow +\infty}\dfrac{2}{x-3}=0$

 

Donc la droite d'équation $y=2x-1$ est asymptote (oblique)à la courbe de $f.$

$$f'(x)=2-\dfrac{2}{(x-3)^{2}}=\dfrac{2\left[(x-3)^{2}-1\right]}{(x-3)^{2}}=\dfrac{2(x-4)(x-2)}{(x-3)^{2}}$$

 

Nous avons le tableau de variation suivant :

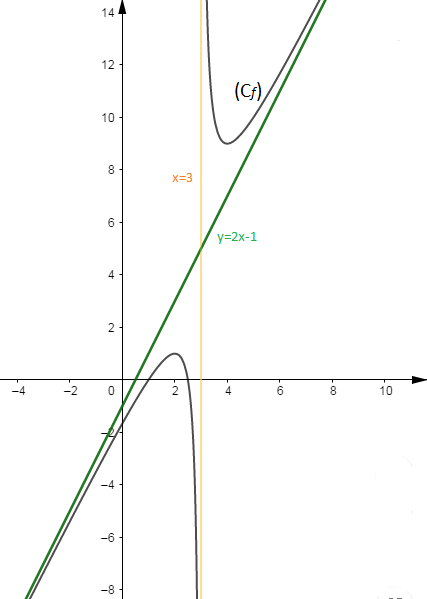
Il faut des points pour dessiner la courbe donc il faut en chercher et il faut dessiner les asymptotes. 

 

On démontre aisément que le point de rencontre des asymptotes est centre de symétrie pour la courbe.

 

On peut étudier la position de la courbe et de son asymptote en étudiant le signe de $\left(f(x)-(2x-1)\right)=\dfrac{2}{x-3}$

 

Lorsque la différence est positive, la courbe est au dessus de la droite et lorsque la différence est négative, la courbe est en dessous de la droite

5) soit la fonction $f$ définie par :

$$f(x)=\left\lbrace\begin{array}{ll} \dfrac{1}{3}x^{3}-x+\dfrac{2}{3}&\text{si }x<2\\ \\ \dfrac{x^{2}}{x+1}&\text{si }x\geq 2 \end{array}\right.$$

 

1) Donner l'ensemble de définition de $f.$

 

2) Calculer les limites de $f$ aux bornes de son ensemble de définition.

 

3) Étudier la continuité et la dérivabilité de en $x=2.$ 

 

Donner la conséquence graphique de l'étude de la dérivabilité de $f$ en $x=2.$

 

4) Calculer $f'(x)$ dans chaque intervalle où $f$ est dérivable et étudier le signe de $f'(x).$ 

 

Dresser le tableau de variations de $f.$

 

5) Étudier les branches infinies de la courbe de $f$ et préciser les asymptotes éventuelles.

 

6) Tracer la courbe de $f$ ainsi que toutes les droites remarquables rencontrées au cours de l'étude de $f.$

Sur $]-\infty\;;\ 2[$ $f$ est définie par un polynôme donc définie en tout point de cet intervalle.

 

Sur $[2\;;\ +\infty[$ $f$ est définie par une fonction rationnelle dont le dénominateur s'annule pour $x=-1$ donc définie en tout point de cet intervalle. 

 

D'où, $\mathcal{D}_{f}=\mathbb{R}.$

 

$\lim_{x\rightarrow -\infty}f(x)=\lim_{x\rightarrow -\infty}\left(\dfrac{1}{3}x^{3}-x+\dfrac{2}{3}\right)=-\infty$

 

$\lim_{x\rightarrow +\infty}f(x)=\lim_{x\rightarrow +\infty}\dfrac{x^{2}}{x+1}=+\infty$

 

$\lim_{x\rightarrow 2^{-}}f(x)=\lim_{x\rightarrow 2}\left(\dfrac{1}{3}x^{3}-x+\dfrac{2}{3}\right)=\dfrac{4}{3}$

 

$\lim_{x\rightarrow 2^{+}}f(x)=\lim_{x\rightarrow 2}\dfrac{x^{2}}{x+1}=\dfrac{4}{3}=f(2)$

 

$\lim_{x\rightarrow 2^{-}}f(x)=\lim_{x\rightarrow 2^{+}}f(x)=f(2)\;,\ f$ est donc continue en $x=2.$

 

$f$ est dérivable sur $\mathbb{R}$ privé de $2$ et :

$$f'(x)=\left\lbrace\begin{array}{ll} x^{2}-1&\text{si }x<2\\ \\ \dfrac{x^{2}+2x}{(x+1)^{2}}&\text{si }x\geq 2 \end{array}\right.$$

 

Pour $x<2$ la dérivée s'annule pour $x=-1$ et $x=1.$ 

 

Pour $x\geq 2$ la dérivée s'annule pour $x=-2$ et $x=0$ qui n'appartiennent pas à cet intervalle donc la dérivée ne s'annule pas dans cet intervalle.

 

Cela donne le tableau de variations suivant :

En $-\infty$ la branche infinie est une branche parabolique de direction l'axe des ordonnées (car nous avons un polynôme)

 

En $+\infty$ $f(x)$ peut s'écrire $f(x)=x-1+\dfrac{1}{x+1}$ par division euclidienne du numérateur par le dénominateur. 

 

Donc $\lim_{x\rightarrow +\infty}\left(f(x)-(x-1)\right)=\lim_{x\rightarrow +\infty}\dfrac{1}{x+1}=0$ et par suite la droite d'équation réduite $y=x-1$ est asymptote oblique de la courbe en $+\infty.$

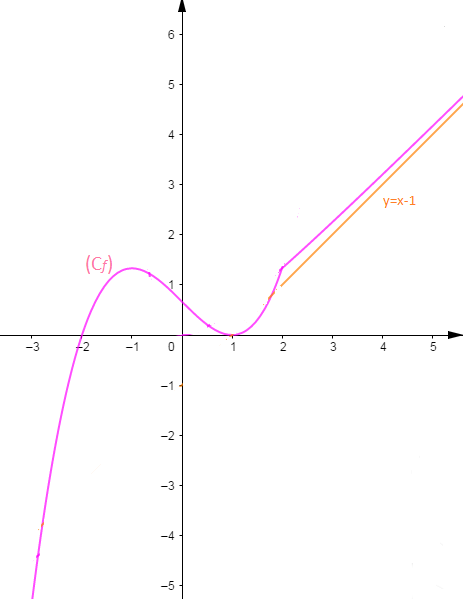
Remarquons que comme pour toute courbe, la représentation graphique nécessite la recherche de quelques points en dehors de ceux qui pourraient intervenir sur le tableau de variations.