Vous êtes ici

Solution des exercices : Statistique 3e

Classe:

Troisième

Exercice 1 BFEM 1994

Voici les tailles en $cm$ des vingt élèves d'une classe de 3e.

\begin{array}{cccccccccc} 165 & 145 & 150 & 166 & 165 & 160 & 158 & 162 & 165 & 150 \\ 158 & 165 & 154 & 158 & 160 & 162 & 162 & 154 & 165 & 160 \end{array}

1) a) L'étude porte sur des élèves d'une classe de 3e.

Donc, la population étudiée trouve être les élèves d'une classe de 3e.

b) Le caractère étudié est la taille.

La taille étant une grandeur mesurable donc, ce caractère est de nature quantitative.

2) Dressons le tableau des : $\text{Effectifs}\;;\ E.C.C\;;\ E.C.D\;;\ \text{Fréquences}\;;\ F.C.C\ $ et $\ F.C.D$ en $\%.$

\begin{array}{lcccccccc} Taille en c m & 145 & 150 & 154 & 158 & 160 & 162 & 165 & 166 \\ Effectifs & 1 & 2 & 2 & 3 & 3 & 3 & 5 & 1 \\ E . C . C & 1 & 3 & 5 & 8 & 11 & 14 & 19 & 20 \\ E . C . D & 20 & 19 & 17 & 15 & 12 & 9 & 6 & 1 \\ Fréquences en % & 5 & 10 & 10 & 15 & 15 & 15 & 25 & 5 \\ F . C . C en % & 5 & 15 & 25 & 40 & 55 & 70 & 95 & 100 \\ F . C . D en % & 100 & 95 & 85 & 75 & 60 & 45 & 30 & 5 \end{array}

3) a) D'après la ligne des $E.C.C$, on constate que $8$ élèves ont au plus $158\;cm.$

b) D'après la ligne des $E.C.D$, on trouve $12$ élèves qui ont plus de $158\;cm.$

4) a) Le mode de la série statistique est caractérisé par la modalité $165.$

Le mode d'une série statistique correspond à la modalité qui a le plus grand effectif.

b) Calculons la taille moyenne de cette série

La moyenne $M$ d'une série statistique à caractère quantitatif est égale au quotient de la somme de toutes les valeurs prises par le caractère par l'effectif total de la population.

Ainsi, on peut écrire :

M = \frac{total des "Produits"}{effectif total}

Par suite,

\begin{array}{rcl} M & = & \frac{1 \times 145 + 2 \times 150 + 2 \times 154 + 3 \times 158 + 3 \times 160 + 3 \times 162 + 5 \times 165 + 1 \times 166}{20} \\ = & \frac{145 + 300 + 308 + 474 + 480 + 486 + 825 + 166}{20} \\ = & \frac{3184}{20} \\ = & 159.2 \end{array}

D'où, $\boxed{M=159.2\;cm}$

Cette valeur de $M$ représente la taille de référence pour cette classe de 3e.

Cela signifie que la plupart des élèves ont une taille très proche de $159.2\;cm.$

Exercice 2 BFEM BLANC 2005

Le tableau ci-dessous représente les tailles de 40 élèves d'une classe de 3e.

\begin{array}{lccccc} Tailles en c m & [140; 150 [ & [150; 160 [ & [160; 170 [ & [170; 180 [ & [180; 190 [ \\ Effectifs & 8 & 5 & 18 \\ Fréquences en % \\ F.C.C en % \\ F.C.D en % \end{array}

1) Complétons le tableau sachant que l'effectif de la classe $[140\;;\ 150[$ est la moitié de $[180\;;\ 190[.$

Soit $x$ l'effectif de la classe $[140\;;\ 150[$ et $y$ l'effectif de la classe $[180\;;\ 190[$

Alors, $x=\dfrac{y}{2}\ $ soit : $2x=y\qquad(1)$

De plus, l'effectif total de la classe étant $40$ alors, cela signifie :

$x+8+5+18+y=40\ $ soit : $x+y=9\qquad(2)$

Les équations (1) et (2) forment alors un système dont la solution constitue les valeurs exactes de $x$ et de $y.$

Soit donc à résoudre le système suivant :

{\begin{array}{rcl} 2 x & = & y (1) \\ x + y & = & 9 (2) \end{array}

En remplaçant $y$ par $2x$ dans l'équation (2), on obtient :

\begin{array}{rcl} x + y = 9 & \Rightarrow & x + 2 x = 9 \\ \Rightarrow & 3 x = 9 \\ \Rightarrow & x = \frac{9}{3} \\ \Rightarrow & x = 3 \end{array}

Donc, $\boxed{x=3}$

Pour déterminer $y$, on remplace cette valeur trouvée de $x$ dans l'équation (1).

On a : $2x=y$ donc, $y=2\times 3=6$

Ainsi, $\boxed{y=6}$

Par conséquent :

\begin{array}{lccccc} Tailles en c m & [140; 150 [ & [150; 160 [ & [160; 170 [ & [170; 180 [ & [180; 190 [ \\ Effectifs & 3 & 8 & 5 & 18 & 6 \\ Fréquences en % & 7.5 & 20 & 12.5 & 45 & 15 \\ F.C.C en % & 7.5 & 27.5 & 40 & 85 & 100 \\ F.C.D en % & 100 & 92.5 & 72.5 & 60 & 15 \end{array}

2) Déterminons le pourcentage d'élèves dont la taille est inférieure à $1.80\;m$ et supérieure à $150\;cm.$

On a : $1.80\;m=180\;cm$ alors, sur le tableau ci-dessus, d'après la ligne des fréquences, on constate que les tailles inférieures à $180\;cm$ et supérieures à $150\;cm$ correspondent à :

20 % + 12.5 % + 45 % = 77.5 %

Donc, $77.5\%$ des élèves ont une taille inférieure à $1.80\;m$ et supérieure à $150\;cm.$

3) Déterminons le nombre d'élèves qui ont une taille au moins égale à $160\;cm$

Sur la ligne des $\text{F.C.D}$, on remarque que $72.5\%$ des élèves ont une taille au moins égale à $160\;cm.$

Ce qui correspond à :

n = \frac{72.5}{100} \times 40 = 0.725 \times 40 = 29

Donc, 29 élèves ont une taille au moins égale à $160\;cm$

4) La classe médiane de cette série est donnée par :

[170; 180 [

En effet, l'effectif total étant $40$ alors, sa moitié est égale à $20.$

Donc, la médiane de cette série correspond à la $20^{e}$ valeur de la taille et cette valeur appartient à la classe $[170\;;\ 180[.$

D'où, $[170\;;\ 180[$ représente la classe médiane de cette série.

5) Déterminons le nombre d'élève qui ont une taille supérieure à la taille moyenne.

Pour cela, déterminons d'abord la taille moyenne.

Comme nous avons une série statistique à caractère quantitatif continu, groupée en classes d'amplitude 10 alors, nous allons utiliser les centres de ces classes pour calculer la moyenne de la série.

Soient :

$\ast\ \ C_{1}\;,\ C_{2}\;,\ C_{3}\;,\ C_{4}\ $ et $\ C_{5}$ les centres respectifs de ces classes.

$\ast\ \ n_{1}\;,\ n_{2}\;,\ n_{3}\;,\ n_{4}\ $ et $\ n_{5}$ les effectifs partiels respectifs et $N$ l'effectif total.

$\ast\ \ f_{1}\;,\ f_{2}\;,\ f_{3}\;,\ f_{4}\ $ et $\ f_{5}$ les fréquences respectives

Alors, on a :

\begin{array}{rcl} M & = & \frac{n_{1} \times C_{1} + n_{2} \times C_{2} + n_{3} \times C_{3} + n_{4} \times C_{4} + n_{5} \times C_{5}}{N} \\ = & \frac{n_{1}}{N} C_{1} + \frac{n_{2}}{N} C_{2} + \frac{n_{3}}{N} C_{3} + \frac{n_{4}}{N} C_{4} + \frac{n_{5}}{N} C_{5} \\ = & f_{1} C_{1} + f_{2} C_{2} + f_{3} C_{3} + f_{4} C_{4} + f_{5} C_{5} \end{array}

Les centres sont donnés dans le tableau suivant :

\begin{array}{lccccc} Tailles en c m & [140; 150 [ & [150; 160 [ & [160; 170 [ & [170; 180 [ & [180; 190 [ \\ Effectifs & 3 & 8 & 5 & 18 & 6 \\ Fréquences en % & 7.5 & 20 & 12.5 & 45 & 15 \\ F.C.C en % & 7.5 & 27.5 & 40 & 85 & 100 \\ F.C.D en % & 100 & 92.5 & 72.5 & 60 & 15 \\ Centres & 145 & 155 & 165 & 175 & 185 \end{array}

Par suite, $M=0.075\times 145+0.20\times 155+0.125\times 165+0.45\times 175+0.15\times 185=169$

Donc, $\boxed{M=169\;cm}$

Par conséquent, d'après la ligne des $\text{F.C.D}$, on constate que $60\%$ des élèves ont une taille supérieure à la taille moyenne.

Ce qui correspond à :

n = \frac{60}{100} \times 40 = 0.6 \times 40 = 24

Donc, 24 élèves ont une taille supérieure à la taille moyenne.

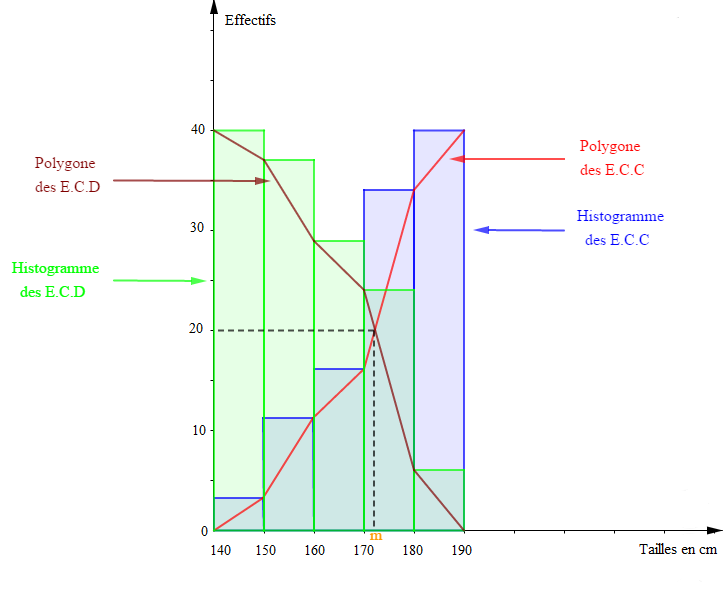
6) Construisons les histogrammes cumulatifs dans un même repère.

On prendra comme échelle :

\begin{array}{rcl} 1 c m & ⟶ & 10 c m \\ 1 c m & ⟶ & 5 élèves \end{array}

7) Faisons apparaître les polygones et déterminons graphiquement la médiane puis interprétons le résultat.

Le point de rencontre des deux polygones constitue le point médian.

Donc, son abscisse $m$ correspond exactement à la médiane.

Ainsi, en tenant compte de l'échelle, on trouve : $m=172$

Par ailleurs, l'ordonnée du point médian correspond à la moitié de l'effectif total.

Par conséquent, cette valeur médiane partage les élèves de la classe en deux groupes de même effectif.

$\ast\ $ un premier groupe de 20 élèves de taille inférieure à $172\;cm$

$\ast\ $ un second groupe de 20 élèves de taille supérieure à $172\;cm$

Exercice 3 BFEM 2006

Pour préparer une "opération Tabaski", un éleveur pèse ses 30 moutons afin de les répartir par catégories de poids, en quatre classes de poids, d'amplitude $4\;kg$, qu'il désigne respectivement par : "4e choix" ; "3e

choix" ; "2e choix" ; "1e choix".

Le relevé ci-dessous donne le poids en kilogramme des moutons pesés :

\begin{array}{cccccccccc} 50 & 52 & 52.5 & 54.5 & 52 & 59 & 58 & 55 & 55.5 & 56 \\ 55 & 55 & 57 & 58 & 58.5 & 60 & 60.5 & 65 & 63 & 60 \\ 61 & 65 & 64 & 65 & 55 & 59 & 58 & 59 & 59.5 & 65 \end{array}

1) Donnons les classes de cette répartition

Comme la borne inférieure de la première classe de poids est 50 et que les classes sont d'amplitude $4\;kg$ alors, en ajoutant 4 à 50 on trouve la seconde borne de la première classe.

Donc, la première classe sera donnée par :

[50; 54 [

En procédant de la même manière on obtient les autres classes :

[54; 58 [, [58; 62 [, [62; 66 [

2) Dressons le tableau des effectifs de la série groupée en classes obtenue.

\begin{array}{ccccc} Classes & [50; 54 [ & [54; 58 [ & [58; 62 [ & [62; 66 [ \\ Effectifs & 4 & 8 & 12 & 6 \end{array}

Déterminons la classe médiane.

En effet, la moitié de l'effectif étant est égale à 15. Or, le 15e mouton dans l'ordre du décompte appartient à la classe $[58\;;\ 62[.$

Donc, la classe médiane est la classe $[58\;;\ 62[$

3) On suppose dans la suite que le tableau des effectifs obtenu est :

\begin{array}{ccccc} "4e choix" & "3e choix" & "2e choix" & "1e choix" \\ Classes & [50; 54 [ & [54; 58 [ & [58; 62 [ & [62; 66 [ \\ Nombre de moutons : & 4 & 8 & 12 & 6 \\ Effectifs \end{array}

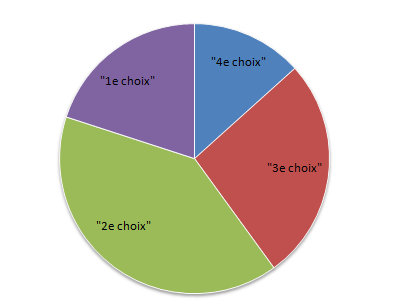
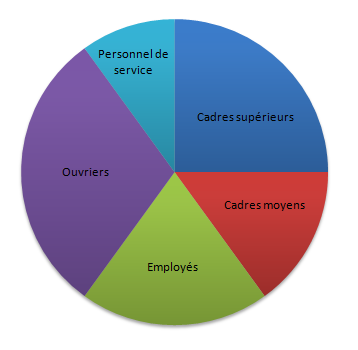
Dessinons le diagramme circulaire de cette série.

On sait que l'angle d'occupation $\alpha^{\circ}$ de chaque classe est donné par :

α^{\circ} = \frac{360^{\circ} \times n}{N}

où, $n$ est l'effectif partiel et $N$ effectif total.

Ces angles d'occupation sont donnés dans le tableau ci-dessous :

\begin{array}{ccccc} "4e choix" & "3e choix" & "2e choix" & "1e choix" \\ Classes & [50; 54 [ & [54; 58 [ & [58; 62 [ & [62; 66 [ \\ Effectifs & 4 & 8 & 12 & 6 \\ α^{\circ} & 48 & 96 & 144 & 72 \end{array}

Nous obtenons diagramme circulaire ci-dessous :

4) Déterminons le prix de vente d'un mouton "3e choix" $(P_{3})$

Soient :

$\ast\ \ P_{1}$ le prix de vente d'un mouton "1er choix" $(70000\;\text{F})$

$\ast\ \ P_{2}$ le prix de vente d'un mouton "2e choix" $(65000\;\text{F})$

$\ast\ \ P_{3}$ le prix de vente d'un mouton "3e choix"

$\ast\ \ P_{4}$ le prix de vente d'un mouton "4e choix" $(52000\;\text{F})$

$\ast\ \ P_{m}$ le prix de vente moyen des moutons $(62000\;\text{F})$

$\ast\ \ n_{1}\;;\ n_{2}\;;\ n_{3}\;;\ n_{4}$ les effectifs respectifs des classes

On a alors :

P_{m} = \frac{n_{1} \times P_{1} + n_{2} \times P_{2} + n_{3} \times P_{3} + n_{4} \times P_{4}}{n_{1} + n_{2} + n_{3} + n_{4}}

Donc, $62000=\dfrac{6\times 70000+12\times 65000+8\times P_{3}+4\times 52000}{30}$

Par suite,

\begin{array}{rcl} 62000 \times 30 & = & 6 \times 70000 + 12 \times 65000 + 8 \times P_{3} + 4 \times 52000 \\ 1860000 & = & 420000 + 780000 + 8 P_{3} + 208000 \\ 8 P_{3} & = & 1860000 - 420000 - 780000 - 208000 \\ 8 P_{3} & = & 452000 \\ P_{3} & = & \frac{452000}{8} \\ P_{3} & = & 56500 \end{array}

Par conséquent, un mouton "3e choix" sera vendu au prix de $56500\;\text{F}$

Exercice 4 BFEM 2007

Le tableau ci-dessous donne la répartition des joueurs d'une équipe de football, selon la taille en $m\ :$

\begin{array}{ccccc} Tailles & [1.65; 1.75 [ & [1.75; 1.85 [ & [1.85; 1.95 [ & [1.95; 2.05 [ \\ Effectifs & 6 & 15 & 20 & 9 \end{array}

1) Complétons le tableau en y faisant figurer : $E.C.D\;;\ F$ en $\%$ et $F.C.C.$

\begin{array}{lcccc} Tailles & [1.65; 1.75 [ & [1.75; 1.85 [ & [1.85; 1.95 [ & [1.95; 2.05 [ \\ Effectifs & 6 & 15 & 20 & 9 \\ E . C . D & 50 & 44 & 29 & 9 \\ F en % & 12 & 30 & 40 & 18 \\ F . C . C en % & 12 & 42 & 82 & 100 \\ Centres & 1.70 & 1.80 & 1.90 & 2 \end{array}

2) Déterminons le nombre de joueurs qui ont une taille au moins égale à $1.75\;m$

D'après la ligne des $E.C.D$, on constate que 44 joueurs ont une taille au moins égale à $1.75\;m$

3) Donnons la taille moyenne dans cette équipe en centimètre prés par défaut.

Comme nous avons une série statistique à caractère quantitatif continu, groupée en $4$ classes alors, nous allons utiliser les centres de ces classes pour calculer la moyenne de la série.

Soient :

$\ast\ \ C_{1}\;,\ C_{2}\;,\ C_{3}\ $ et $\ C_{4}$ les centres respectifs de ces classes.

$\ast\ \ n_{1}\;,\ n_{2}\;,\ n_{3}\ $ et $\ n_{4}$ les effectifs partiels respectifs et $N$ l'effectif total.

Les centres sont donnés dans le tableau ci-dessus.

Soit $M$ la taille moyenne alors, on a :

M = \frac{n_{1} \times C_{1} + n_{2} \times C_{2} + n_{3} \times C_{3} + n_{4} \times C_{4}}{N}

Par suite,

\begin{array}{rcl} M & = & \frac{6 \times 1.7 + 15 \times 1.8 + 20 \times 1.9 + 9 \times 2}{50} \\ = & \frac{10.2 + 27 + 38 + 18}{50} \\ = & \frac{93.2}{50} \\ = & 1.864 \end{array}

Ainsi, la taille moyenne est de $1.86\;m$

4) Indiquons la classe modale de cette série statistique.

On constate que le plus grand effectif $(20)$ se trouve dans la classe $[1.85\;;\ 1.95[.$

Par conséquent, cette classe constitue la classe modale de cette série statistique.

Exercice 5 BFEM 2009

1e Partie :

Le tableau statistique ci-dessous donne la répartition de notes d'élèves obtenues lors d'un examen.

1) Complétons le tableau

\begin{array}{lcccccccccccccccc} Notes & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16 & 17 \\ Effectifs & 2 & 1 & 1 & 2 & 3 & 2 & 4 & 6 & 7 & 6 & 5 & 3 & 2 & 3 & 2 & 1 \\ E.C.C & 2 & 3 & 4 & 6 & 9 & 11 & 15 & 21 & 28 & 34 & 39 & 42 & 44 & 47 & 49 & 50 \\ E.C.D & 50 & 48 & 47 & 46 & 44 & 41 & 39 & 35 & 29 & 22 & 16 & 11 & 8 & 6 & 3 & 1 \\ F en % & 4 & 2 & 2 & 4 & 6 & 4 & 8 & 12 & 14 & 12 & 10 & 6 & 4 & 6 & 4 & 2 \\ F.C.C en % & 4 & 6 & 8 & 12 & 18 & 22 & 30 & 42 & 56 & 68 & 78 & 84 & 88 & 94 & 98 & 100 \end{array}

$\ast\ \ $ L'effectif de la modalité $6$ représente le nombre d'élèves qui ont obtenu la note $6$ lors de cet examen.

$\ast\ \ $ Le $E.C.C$ de la modalité $8$ représente le nombre d'élèves qui ont obtenu une note inférieure ou égale à $8$, lors de cet examen.

$\ast\ \ $ Le $E.C.D$ de la modalité $5$ représente le nombre d'élèves qui ont obtenu une note supérieure ou égale à $5$, lors de cet examen.

$\ast\ \ $ La $F.C.C$ de la modalité $16$ représente le pourcentage d'élèves qui ont obtenu une note inférieure à $17$, lors de cet examen.

3) Déduisons de ce tableau le pourcentage des élèves qui ont moins de $14.$

D'après la ligne des $F.C.C$, on constate que la modalité $13$ a une $F.C.C$ égale à $84.$

Ce qui signifie que $84\%$ des élèves ont obtenu une note inférieure ou égale à $13$, lors de cet examen.

Autrement dit, $84\%$ des élèves ont moins de $14.$

2e Partie :

On groupe les notes précédentes en classes d'amplitude 4 dans le tableau ci-dessous.

1) Complétons le tableau.

\begin{array}{lccccc} Notes & [0; 4 [ & [4; 8 [ & [8; 12 [ & [12; 16 [ & [16; 20 [ \\ Effectifs & 3 & 8 & 23 & 13 & 3 \\ E.C.C & 3 & 11 & 34 & 47 & 50 \\ Centres & 2 & 6 & 10 & 14 & 18 \end{array}

2) Calculons la moyenne des notes obtenues par ces élèves.

Soit $M$ cette moyenne et soient :

$\ast\ \ C_{1}\;,\ C_{2}\;,\ C_{3}\;;\ C_{4}$ et $\ C_{5}$ les centres respectifs des classes de notes.

$\ast\ \ n_{1}\;,\ n_{2}\;,\ n_{3}\;;\ n_{4}$ et $\ n_{5}$ les effectifs partiels respectifs et $N$ l'effectif total.

Les centres sont donnés dans le tableau ci-dessus.

On a :

M = \frac{n_{1} \times C_{1} + n_{2} \times C_{2} + n_{3} \times C_{3} + n_{4} \times C_{4} + n_{5} \times C_{5}}{N}

Par suite,

\begin{array}{rcl} M & = & \frac{3 \times 2 + 8 \times 6 + 23 \times 10 + 13 \times 14 + 3 \times 18}{50} \\ = & \frac{6 + 48 + 230 + 182 + 54}{50} \\ = & \frac{520}{50} \\ = & 10.4 \end{array}

D'où, la moyenne des notes obtenues est égale à $10.4$

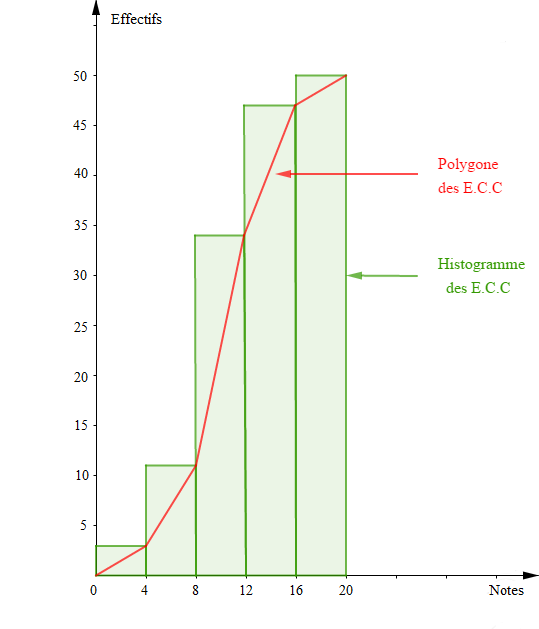
3) Construisons l'histogramme des effectifs cumulés croissants.

Exercice 6 BFEM 2008

\begin{array}{cccccc} Nombre de jours à l'hôtel & 2 & 3 & 4 & 5 & 6 \\ Effectifs cumulés décroissants & 180 & 90 & 50 & 20 & 15 \end{array}

Le tableau statistique ci-dessus est réalisé par la direction commerciale d'un hôtel qui a reçu des invités lors du dernier sommet de $\text{l'O.C.I}$ organisé à Dakar.

1) En effet, l'étude porte sur des invités reçu dans un hôtel lors du dernier sommet de $\text{l'O.C.I}$ organisé à Dakar.

La population étudiée est alors les invités du dernier sommet de $\text{l'O.C.I}$ organisé à Dakar.

2) Indiquons le caractère étudié et précisons sa nature.

Le caractère étudié est le nombre de jours passés à l'hôtel.

Comme le nombre de jours est une grandeur mesurable alors, ce caractère est de nature quantitative.

3) Déterminons la médiane de cette série.

On rappelle que la médiane d'une série statistique à caractère quantitatif est la valeur de ce caractère qui sépare la population en deux parties de même effectif.

Alors, en suivant la ligne des effectifs cumulés décroissants, nous constatons que l'effectif total de cette série est : $N=180.$

Par suite, sa moitié est égale à $\dfrac{180}{2}=90.$

Donc, la médiane $m$ de cette série est donnée par :

m = \frac{Nombre de jours du 90e invité + Nombre de jours du 91e invité}{2}

Or, en ajoutant dans le tableau statistique ci-dessus, la ligne des effectifs, on obtient :

\begin{array}{lccccc} Nombre de jours à l'hôtel & 2 & 3 & 4 & 5 & 6 \\ Effectifs cumulés décroissants & 180 & 90 & 50 & 20 & 15 \\ Effectifs & 90 & 40 & 30 & 5 & 15 \end{array}

Donc, d'après ce tableau, nous remarquons que la $90e$ et la $91e$ invité, dans l'ordre du décompte, ont passé à l'hôtel $2\,j\ $ et $\ 3\,j$ respectivement.

Ainsi, $m=\dfrac{2+3}{2}=\dfrac{5}{2}=2.5$

D'où, la médiane de cette série est égale à $2$ jours et demi.

Ce qui signifie alors :

$90$ invités ont passé à l'hôtel un nombre de jours inférieur à $2.5$

$90$ invités ont passé à l'hôtel un nombre de jours supérieur à $2.5$

4) a) Calculons le pourcentage des invités qui ont passé au moins $3$ jours à l'hôtel.

Cela correspond alors au pourcentage des invités qui ont passé à l'hôtel un nombre de jours supérieur ou égal à $3.$

En suivant la ligne des effectifs cumulés décroissants, le pourcentage $f$ des invités qui ont passé au moins 3 jours à l'hôtel est donné par :

\begin{array}{rcl} f & = & \frac{90}{180} \times 100 \\ = & 50 \end{array}

Donc, $50\%$ des invités ont passé au moins $3$ jours à l'hôtel.

b) Calculons le nombre d'invités qui ont passé moins de $4$ jours à l'hôtel.

Cela correspond donc au nombre d'invités qui ont passé à l'hôtel un nombre de jours inférieur à $4.$

Alors, d'après la ligne des effectifs, le nombre $n$ d'invités qui ont passé moins de $4$ jours à l'hôtel est donné par :

\begin{array}{rcl} n & = & 90 + 40 \\ = & 130 \end{array}

Donc, $130$ invités ont passé moins de $4$ jours à l'hôtel.

c) Déterminons le nombre d'invités qui ont passé plus de $4$ jours à l'hôtel.

En suivant la ligne des effectifs cumulés décroissants, le nombre d'invités qui ont passé plus de $4$ jours à l'hôtel est égal à $20.$

Ce qui signifie que $20$ invités ont passé plus de $4$ jours à l'hôtel.

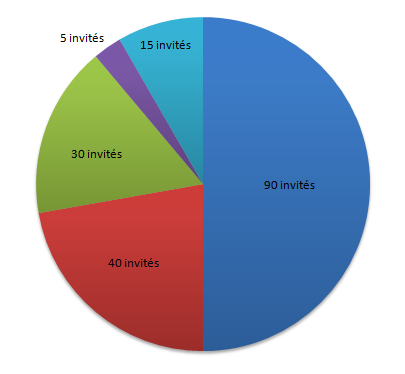
5) Construisons le diagramme circulaire des effectifs de cette série.

On sait que l'angle d'occupation $\alpha^{\circ}$ de chaque effectif partiel est donné par :

α^{\circ} = \frac{360^{\circ} \times n}{N}

où, $n$ est l'effectif partiel et $N$ effectif total.

En ajoutant les angles d'occupation de chaque effectif dans le tableau statistique, on obtient :

\begin{array}{lccccc} Nombre de jours à l'hôtel & 2 & 3 & 4 & 5 & 6 \\ Effectifs cumulés décroissants & 180 & 90 & 50 & 20 & 15 \\ Effectifs & 90 & 40 & 30 & 5 & 15 \\ α^{\circ} & 180^{\circ} & 80^{\circ} & 60^{\circ} & 10^{\circ} & 30^{\circ} \end{array}

Nous obtenons alors le diagramme circulaire ci-dessous :

Exercice 7

Le tableau ci-dessous représente la répartition des notes de mathématiques lors d'un test de niveau où la note moyenne est $12.5$

\begin{array}{lcccccc} Notes sur 20 & 6 & 8 & 9 & 12 & 15 & x \\ Nombre d'élèves & 6 & 9 & 15 & 9 & 15 & 18 \end{array}

1) Calculons $x$, la meilleure note attribuée lors de ce test.

On sait que la note moyenne $M$ est $12.5$

Or, $M=\dfrac{\text{total des "Produits"}}{\text{effectif total}}$

Par suite,

\begin{array}{rcl} M & = & \frac{6 \times 6 + 9 \times 8 + 15 \times 9 + 9 \times 12 + 15 \times 15 + 18 \times x}{6 + 9 + 15 + 9 + 15 + 18} \\ = & \frac{36 + 72 + 135 + 108 + 225 + 18 x}{72} \\ = & \frac{576 + 18 x}{72} \\ = & \frac{32 + x}{4} \end{array}

Donc, on a :

$\left.

\begin{array}{rcc} M & = & 12.5 \\ M & = & \frac{32 + x}{4} \end{array}

\right\rbrace\ \Rightarrow\ \dfrac{32+x}{4}=12.5$

La résolution de cette dernière équation d'inconnue $x$ nous donne la meilleure note.

Soit alors :

\begin{array}{rcrcl} \frac{32 + x}{4} = 12.5 & \Leftrightarrow & 32 + x & = & 4 \times 12.5 \\ \Leftrightarrow & x & = & 50 - 32 \\ \Leftrightarrow & x & = & 18 \end{array}

Donc, $\boxed{x=18}$

D'où, la meilleure note attribuée lors de ce test est $18.$

2) Déterminons le nombre d'élèves qui ont une note au moins égale à $12.$

Cela représente les élèves qui ont une note supérieure ou égale à $12.$

Ce qui correspond à : $n=9+15+18=42$

Donc, $42$ élèves ont une note au moins égale à $12.$

3) Déterminons le pourcentage des élèves qui ont au plus $15.$

Soit :

f = \frac{Nombre d'élèves qui ont au plus 15}{Effectif total}

Or, le nombre d'élèves qui ont au plus $15$ représente les élèves qui ont une note inférieure ou égale à $15.$

Ce qui correspond à : $n'=6+9+15+9+15=54$

Par suite, $f=\dfrac{54}{72}=0.75$

Ainsi, $75\%$ des élèves ont au plus $15$ de note.

4) Déterminons la note médiane.

L'effectif total étant $N=72$ alors, sa moitié est égale à $\dfrac{72}{2}=36.$

Donc, la note médiane $m$ sera donnée par :

m = \frac{note du 36e élève + note du 37e élève}{2}

Or, le $36e$ et le $37e$ élève dans l'ordre du décompte ont obtenu la note $12.$

Par suite, $m=\dfrac{12+12}{2}=\dfrac{24}{2}=12$

D'où, la note médiane pour ce test de niveau est égale à $12.$

Exercice 8 BFEM 1997

Sur une période donnée les recettes d'une essencerie se répartissent comme suit :

\begin{array}{ccccc} Carburant & Essence ordinaire & Essence super & Gasoil & Mélange \\ Pourcentage \\ de toutes & 30 % & 25 % & 40 % & 5 % \\ les recettes \end{array}

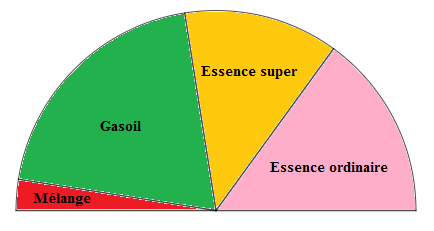
1) Représentons cette série par un diagramme semi-circulaire.

Soit $\alpha^{\circ}$ l'angle d'occupation correspondant à chaque catégorie de carburant. Alors, on a :

α^{\circ} = \frac{n \times 180^{\circ}}{N}

où, $n$ est le pourcentage partiel de recette et $N=100\%$ le pourcentage total.

En ajoutant les angles d'occupation de chaque catégorie de carburant dans le tableau statistique, on obtient :

\begin{array}{ccccc} Carburant & Essence ordinaire & Essence super & Gasoil & Mélange \\ Pourcentage \\ de toutes & 30 % & 25 % & 40 % & 5 % \\ les recettes \\ α^{\circ} & 54^{\circ} & 45^{\circ} & 72^{\circ} & 9^{\circ} \end{array}

Nous obtenons alors le diagramme semi-circulaire ci-dessus.

$\text{Diagramme semi-circulaire}$

2) Sachant que l'essence ordinaire vendue a rapporté $126\,000$ francs et que $42$ litres de mélange ont été vendus, trouvons :

a) La somme rapportée par le gasoil

Soit : $R$ les recettes totales de cette essencerie.

Comme l'essence ordinaire vendue a rapporté $126\,000$ francs et que cette somme représente $30\%$ des recettes totales de cette essencerie alors, cela se traduit par :

126 000 = \frac{30}{100} \times R

Ainsi, $R=\dfrac{126\,000\times 100}{30}=420\,000$

Les recettes totales s'élèvent alors à $420\,000$ francs.

Or, la somme rapportée par le gasoil représente $40\%$ des recettes totales.

Donc, si $R_{g}$ est la somme rapportée par le gasoil alors, on a :

R_{g} = \frac{40}{100} \times R

Ce qui donne :

\begin{array}{rcl} R_{g} & = & \frac{40}{100} \times 420 000 \\ = & \frac{40 \times 420 000}{100} \\ = & 168 000 \end{array}

Ainsi, $\boxed{R_{g}=168\,000\;\text{francs}}$

Le gasoil a donc rapporté $168\,000$ francs.

b) Le prix du litre de mélange

On sait que la somme rapportée par le mélange représente $5\%$ des recettes totales.

Soit $R_{m}$ les recettes du mélange alors, on a :

R_{m} = \frac{5}{100} \times R

Par suite, $R_{m}=\dfrac{5}{100}\times 420\,000=21\,000$

Ainsi, le mélange a rapporté $21\,000$ francs.

Comme $42$ litres de mélange ont été vendus alors, le prix $P$ d'un litre de mélange sera donné par :

P = \frac{R_{m}}{42}

Ce qui donne : $P=\dfrac{21\,000}{42}=500$

Ainsi, un litre de mélange coûte $500$ francs.

Exercice 9

Une entreprise a effectué une étude sur l'âge de ses clients en les classant par tranche d'amplitude 5 ans.

\begin{array}{ccccccccc} Age & [15; 20 [ & [20; 25 [ & [25; 30 [ & [30; 35 [ & [35; 40 [ & [40; 45 [ & [45; 50 [ & [50; 55 [ \\ Effectif & 2 & 5 & 8 & x & 18 & 4 & 6 & 3 \end{array}

1) Sachant que l'étude a porté sur un échantillon de $55$ clients, déterminons l'effectif manquant.

En effet, comme l'étude a porté sur un échantillon de $55$ clients alors, l'effectif total $N=55.$

Par ailleurs, on sait que l'effectif total $N$ est égal à la somme des effectifs partiels.

C'est-à-dire ;

\begin{array}{rcl} N & = & 2 + 5 + 8 + x + 18 + 4 + 6 + 3 \\ = & 46 + x \end{array}

Donc, $N=46+x$

Or, on a : $N=55$

Alors, par comparaison, on obtient :

46 + x = 55

En résolvant cette équation, on trouve l'effectif manquant $x.$

On a :

\begin{array}{rcl} 46 + x = 55 & \Leftrightarrow & x = 55 - 46 \\ \Leftrightarrow & x = 9 \end{array}

Ainsi, l'effectif manquant est $9.$

2) Calculons l'âge moyen des clients, en utilisant le centre des intervalles.

En calculant et en ajoutant le centre de chaque intervalle dans le tableau statistique, on obtient :

\begin{array}{ccccccccc} Age & [15; 20 [ & [20; 25 [ & [25; 30 [ & [30; 35 [ & [35; 40 [ & [40; 45 [ & [45; 50 [ & [50; 55 [ \\ Centre & 17.5 & 22.5 & 27.5 & 32.5 & 37.5 & 42.5 & 47.5 & 52.5 \\ Effectif & 2 & 5 & 8 & 9 & 18 & 4 & 6 & 3 \end{array}

L'âge moyen $M$ des clients est donc donné par :

\begin{array}{rcl} M & = & \frac{2 \times 17.5 + 5 \times 22.5 + 8 \times 27.5 + 9 \times 32.5 + 18 \times 37.5 + 4 \times 42.5 + 6 \times 47.5 + 3 \times 52.5}{55} \\ = & \frac{35 + 112.5 + 220 + 292.5 + 675 + 170 + 285 + 157.5}{55} \\ = & \frac{1947.5}{55} \\ = & 35.409 \end{array}

Ainsi, l'âge moyen des clients est de $35$ ans.

3) Reproduisons le tableau et complétons par la ligne des effectifs cumulés croissants

\begin{array}{ccccccccc} Age & [15; 20 [ & [20; 25 [ & [25; 30 [ & [30; 35 [ & [35; 40 [ & [40; 45 [ & [45; 50 [ & [50; 55 [ \\ Effectif & 2 & 5 & 8 & 9 & 18 & 4 & 6 & 3 \\ E.C.C & 2 & 7 & 15 & 24 & 42 & 46 & 52 & 55 \end{array}

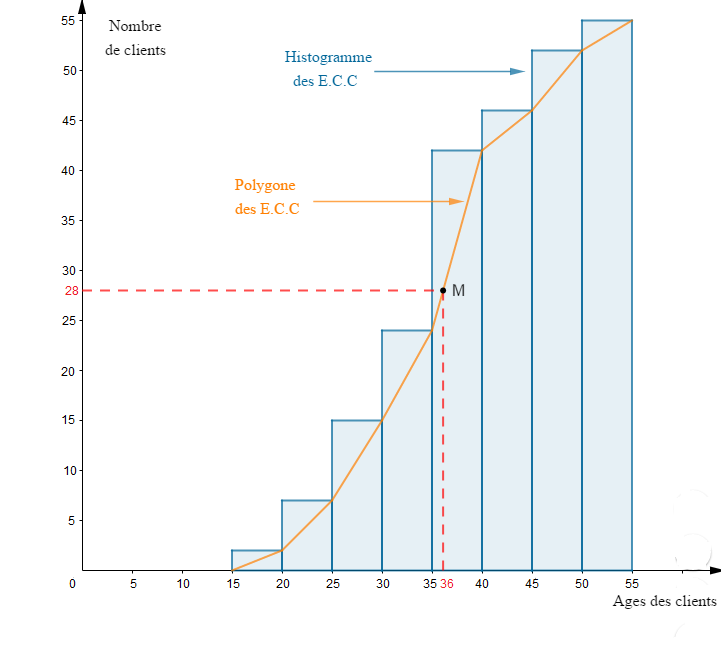
4) Représentons l'histogramme et le polygone des effectifs cumulés croissants.

\begin{array}{lrcl} Echelle : & 1 c m & ⟶ & 5 ans \\ 1 c m & ⟶ & 5 clients \end{array}

$\text{Histogramme et Polygone des E.C.C}$

5) Utilisons le polygone des effectifs cumulés croissants pour déterminer l'âge médian.

On rappelle que la médiane d'une série statistique à caractère quantitatif est la valeur de ce caractère qui sépare la population en deux parties de même effectif.

Comme l'effectif total $N=55$ est un entier impair alors, la position du client qui détermine la valeur médiane de cette série est donnée par :

\frac{N + 1}{2} = \frac{55 + 1}{2} = \frac{56}{2} = 28

Donc, l'âge du $28^{e}$ client, dans l'ordre du décompte, représente l'âge médian de cette série.

Pour déterminer cette valeur médiane, on procède comme suit :

Sur l'axe des ordonnées, on place d'abord la valeur $28.$

Puis, on projette cette valeur sur le polygone des $E.C.C$ parallèlement à l'axe des abscisses.

On obtient le point $M.$

Ensuite, on projette le point $M$ sur l'axe des abscisse, parallèlement à l'axe des ordonnées.

Ce qui donne la valeur $36.$

Donc, l'âge du $28^{e}$ client est de $36$ ans.

Cette valeur représente alors l'âge médian.

Par conséquent, l'âge médian de cette série est de $36$ ans.

Exercice 10

$20$ élèves sautent en hauteur. Les performances sont classées en intervalles d'amplitude $10\;cm.$

\begin{array}{cccccc} Performance & [100; 110 [ & [110; 120 [ & [120; 130 [ & [130; 140 [ & [140; 150 [ \\ Centre \\ Effectifs & X & 4 & 8 & Y & 2 \end{array}

1) Complétons la ligne des centres et précisons la classe modale.

\begin{array}{cccccc} Performance & [100; 110 [ & [110; 120 [ & [120; 130 [ & [130; 140 [ & [140; 150 [ \\ Centre & 105 & 115 & 125 & 135 & 145 \\ Effectifs & X & 4 & 8 & Y & 2 \end{array}

La classe modale de la série statistique est donnée par la classe $[120\;;\ 130[.$

2) la moyenne de cette série est $126.5\;cm$

Déterminons $X\ $ et $\ Y$

En effet, en exprimant l'effectif total $N$ en fonction de $X\ $ et $\ Y$, on obtient :

N = X + 4 + 8 + Y + 2

Or, l'étude porte sur $20$ élèves. Ce qui signifie que $N=20.$

Donc,

\begin{array}{rcl} X + 4 + 8 + Y + 2 = 20 & \Leftrightarrow & X + Y + 14 = 20 \\ \Leftrightarrow & X + Y = 20 - 14 \\ \Leftrightarrow & X + Y = 6 \end{array}

Ainsi, $X\ $ et $\ Y$ vérifient l'équation suivante :

X + Y = 6 (1)

Par ailleurs, comme nous avons une série statistique à caractère quantitatif continu, groupée en classes alors, nous allons utiliser les centres de ces classes pour exprimer la moyenne $M$ de la série en fonction de $X\ $ et $\ Y.$

Ainsi, on a :

\begin{array}{rcl} M & = & \frac{X \times 105 + 4 \times 115 + 8 \times 125 + Y \times 135 + 2 \times 145}{20} \\ = & \frac{105 X + 460 + 1 000 + 135 Y + 290}{20} \\ = & \frac{105 X + 135 Y + 1 750}{20} \\ = & \frac{21 X + 27 Y + 350}{4} \end{array}

Donc, $M=\dfrac{21X+27Y+350}{4}$

Or, on sait que la moyenne de cette série est de $126.5\;cm$ ; ce qui signifie que :

M = \frac{21 X + 27 Y + 350}{4} = 126.5

Par suite, en calculant, on trouve :

\begin{array}{rcl} \frac{21 X + 27 Y + 350}{4} = 126.5 & \Leftrightarrow & 21 X + 27 Y + 350 = 126.5 \times 4 \\ \Leftrightarrow & 21 X + 27 Y + 350 = 506 \\ \Leftrightarrow & 21 X + 27 Y = 506 - 350 \\ \Leftrightarrow & 21 X + 27 Y = 156 \\ \Leftrightarrow & 3 \times (7 X + 9 Y) = 3 \times 52 \\ \Leftrightarrow & 7 X + 9 Y = \frac{3 \times 52}{3} \\ \Leftrightarrow & 7 X + 9 Y = 52 \end{array}

Ainsi, $X\ $ et $\ Y$ vérifient aussi l'équation suivante :

7 X + 9 Y = 52 (2)

Alors, en résolvant le système d'équations formé des équations $(1)\ $ et $\ (2)$, on trouve les valeurs de $X\ $ et $\ Y.$

Soit le système suivant :

{\begin{array}{rcrl} X + Y & = & 6 & (1) \\ 7 X + 9 Y & = & 52 & (2) \end{array}

Alors, en multipliant chaque membre de l'équation $(1)$ par $-7$, le système devient :

{\begin{array}{rcrl} - 7 X - 7 Y & = & - 42 & (3) \\ 7 X + 9 Y & = & 52 & (2) \end{array}

Puis, en additionnant membre à membre les équations $(2)\ $ et $\ (3)$, on trouve :

7 X + 9 Y - 7 X - 7 Y = 52 - 42

Ce qui donne alors : $2Y=10$

D'où, $Y=\dfrac{10}{2}=5$

Ensuite, en remplaçant cette valeur de $Y$ dans l'équation $(1)$, on obtient :

X + 5 = 6

Ce qui entraine : $X=6-5=1$

Ainsi, $\boxed{X=1\ \text{ et }\ Y=5}$

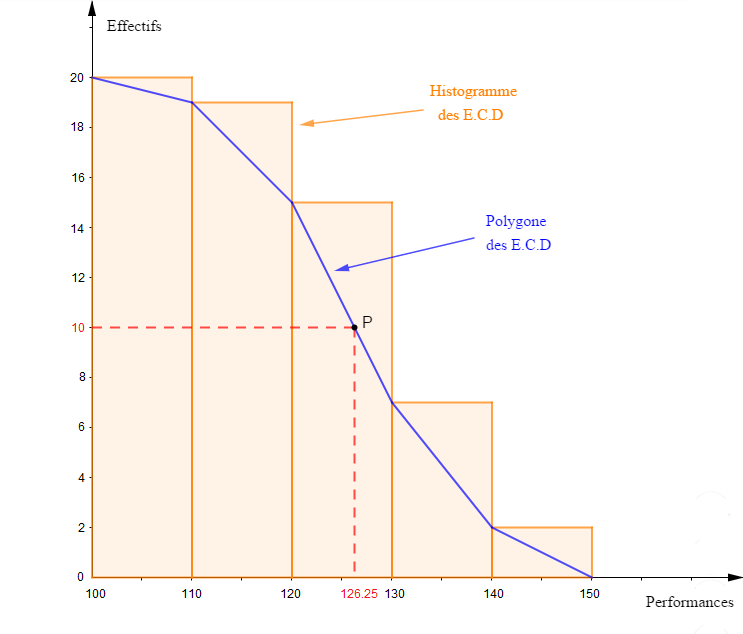
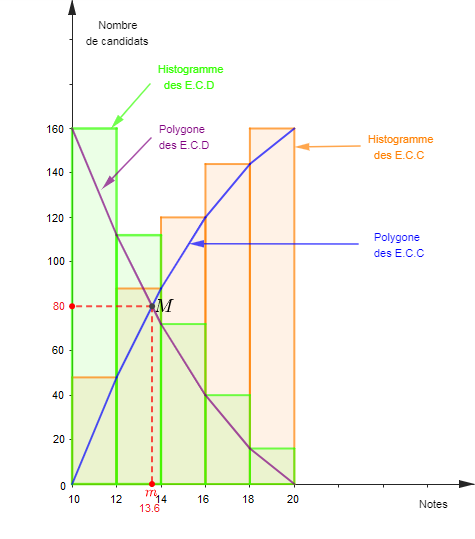
3) a) Construisons l'histogramme des effectifs cumulés décroissants

Pour cela, ajoutons d'abord dans le tableau statistique, la ligne des effectifs cumulés décroissants.

\begin{array}{cccccc} Performance & [100; 110 [ & [110; 120 [ & [120; 130 [ & [130; 140 [ & [140; 150 [ \\ Centre & 105 & 115 & 125 & 135 & 145 \\ Effectifs & 1 & 4 & 8 & 5 & 2 \\ E.C.D & 20 & 19 & 15 & 7 & 2 \end{array}

Ensuite, construisons l'histogramme des $\text{E.C.D}$

\begin{array}{lrcl} Echelle : & 1 c m & ⟶ & 5 c m de saut \\ 1 c m & ⟶ & 2 élèves \end{array}

b) Déterminons graphiquement la performance médiane

Pour cela, nous traçons d'abord, sur le même graphique, le polygone des $\text{E.C.D}$

Comme l'effectif total $N=20$ est un nombre pair alors, la moitié $\dfrac{N}{2}$ qui est égale à $10$ va nous permettre de déterminer la performance médiane.

Ainsi, pour déterminer cette performance médiane, on procède comme suit :

Sur l'axe des ordonnées, on place d'abord la valeur $10.$

Puis, on projette cette valeur sur le polygone des $E.C.D$ parallèlement à l'axe des abscisses.

On obtient le point $P.$

Ensuite, on projette le point $P$ sur l'axe des abscisse, parallèlement à l'axe des ordonnées.

On trouve alors $126.25$ qui représente la valeur médiane de cette série.

Donc, la performance médiane est de $126.25\;cm$

Exercice 11 BFEM 1999

Dans le registre des consultations du dispensaire d'un village, on a relevé les cas du paludisme et on obtient le tableau suivant :

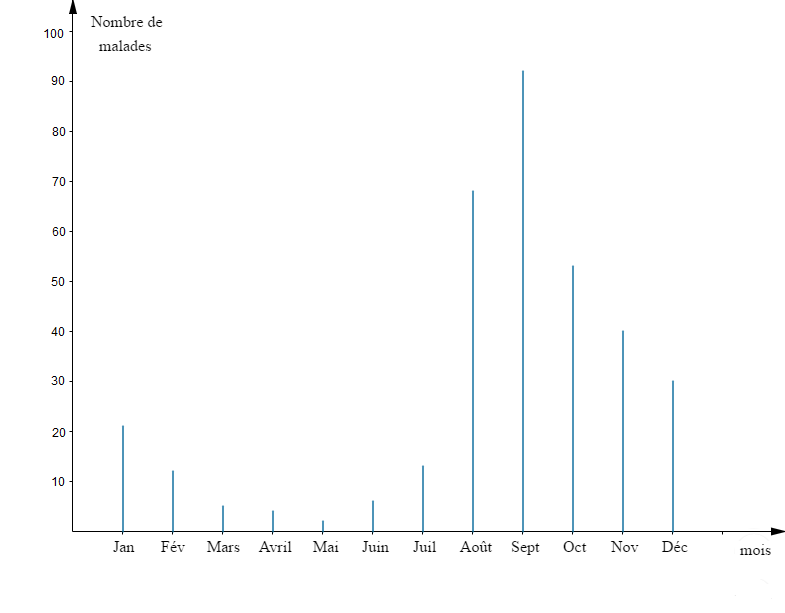
\begin{array}{ccccccccccccc} Mois & Jan & Fév & Mars & Avril & Mai & Juin & Juil & Aout & Sept & Oct & Nov & Déc \\ Nombre \\ de cas & 21 & 12 & 5 & 4 & 2 & 6 & 13 & 68 & 92 & 53 & 40 & 30 \\ Paludisme \end{array}

1) Ajoutons au tableau la ligne des effectifs cumulés croissants.

\begin{array}{ccccccccccccc} Mois & Jan & Fév & Mars & Avril & Mai & Juin & Juil & Aout & Sept & Oct & Nov & Déc \\ Nombre \\ de cas & 21 & 12 & 5 & 4 & 2 & 6 & 13 & 68 & 92 & 53 & 40 & 30 \\ Paludisme \\ E.C.C & 21 & 33 & 38 & 42 & 44 & 50 & 63 & 131 & 223 & 276 & 316 & 346 \end{array}

2) Traçons le diagramme en bâtons de cette série

1 c m représente 10 malades

$\text{Diagramme en bâtons}$

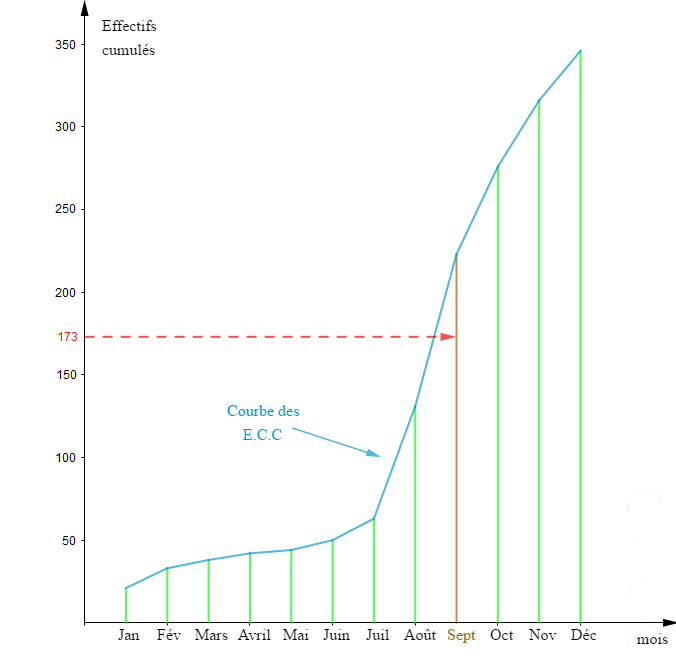
3) Représentons graphiquement la courbe des effectifs cumulés croissants puis, déterminons la période médiane (le mois) pendant laquelle $50\%$ des malades ont été consultés.

2 c m représente 50 malades

$\text{Courbe des effectifs cumulés croissants}$

En effet, en suivant la ligne des $\text{E.C.C}$, on constate que l'effectif total $N$ est égal à $346.$

Alors, la moitié $\dfrac{N}{2}$ qui est égale à $173$ va nous permettre de déterminer la période médiane pendant laquelle $50\%$ des malades ont été consultés.

Ainsi, pour déterminer cette période médiane, on procède comme suit :

Sur l'axe des ordonnées, on place d'abord la valeur $173.$

Puis, on projette cette valeur sur la courbe des $E.C.C$ parallèlement à l'axe des abscisses.

Ensuite, en suivant cette ligne de projection, on croise le diagramme en bâtons au mois de septembre.

Donc, le mois de septembre représente la période médiane de cette série.

4) En moyenne, déterminons le nombre de malades du paludisme par mois.

En effet, si $M$ est le nombre moyen de malades du paludisme par mois alors, $M$ est donné par :

M = \frac{nombre total de malades du paludisme}{nombre total de mois}

Donc, on a : $M=\dfrac{346}{12}\simeq 29$

D'où, en moyenne, nous avons $29$ malades de paludisme par mois.

5) Le paludisme est la maladie qui tue le plus au Sénégal.

Sachant que $10.5\%$ des malades paludisme sont décédés et qu'ils représentent $75\%$ de l'ensemble des cas de décès annuels du dispensaire, calculons :

a) Le nombre de décès de malades du paludisme.

En effet, le nombre total de malades du paludisme est : $N=346.$

Or, on sait que $10.5\%$ des malades paludisme sont décédés.

Cela peut encore s'écrire :

Nombre de décès de malades du paludisme = \frac{10.5}{100} \times N

Donc, on a :

\begin{array}{rcl} Nombre de décès de malades du paludisme & = & \frac{10.5}{100} \times N \\ = & \frac{10.5 \times 346}{100} \\ = & \frac{3 633}{100} \\ ≃ & 36 \end{array}

Ainsi, dans ce dispensaire, $36$ malades du paludisme sont décédés.

b) Le nombre total annuel de malades décédés de ce dispensaire.

Comme ces $36$ décès de malades du paludisme représentent $75\%$ de l'ensemble des cas de décès annuels du dispensaire alors, on peut écrire :

36 = \frac{75}{100} \times Nombre total annuel de malades décédés de ce dispensaire

Ce qui entraine :

Nombre total annuel de malades décédés de ce dispensaire = \frac{36 \times 100}{75}

En calculant, on trouve : $\dfrac{3\,600}{75}=48$

Par conséquent, le nombre total annuel de malades décédés de ce dispensaire est de $48.$

Exercice 12 BFEM 2002

Un conseil régional, voulant octroyer $50$ bourses aux meilleurs élèves des classes de Troisièmes de sa localité, organise un concours à cet effet.

Le montant de la bourse dépend de la note obtenue, laquelle varie de $0$ à $20.$ Ce montant est fixé au maximum à $30\,000\;F.$

Le tableau ci-dessous résulte de la représentation de la série par un diagramme circulaire.

\begin{array}{cccccc} Notes obtenues & [10; 12 [ & [12; 14 [ & [14; 16 [ & [16; 18 [ & [18; 20 [ \\ Montant de \\ la bourse & 10 000 & 15 000 & 20 000 & 25 000 & 30 000 \\ (F CFA) \\ Angles (en degrés) & 108 & 93.5 & \hat{A} & 50.4 & 36 \end{array}

1) Calculons l'angle manquant $\widehat{A}$.

En effet, comme le tableau résulte de la représentation de la série par un diagramme circulaire alors, les angles d'occupation vérifient :

108^{\circ} + {93.5}^{\circ} + \hat{A} + {50.4}^{\circ} + 36^{\circ} = 360^{\circ}

Ce qui entraine : $\widehat{A}=360^{\circ}-108^{\circ}-93.5^{\circ}-50.4^{\circ}-36^{\circ}=72.1^{\circ}$

Donc, $\boxed{\widehat{A}=72.1^{\circ}}$

2) Calculons les effectifs associés aux différents intervalles.

En effet, on sait que l'angle d'occupation $\alpha^{\circ}$ de chaque intervalle vérifie :

α^{\circ} = \frac{360^{\circ} \times n}{N}

où, $n$ est l'effectif partiel et $N$ l'effectif total représenté par le nombre total de bourses à octroyer.

Donc, l'effectif partiel $n$ associé à chaque intervalle est donné par :

n = \frac{α^{\circ} \times N}{360^{\circ}}

Alors, pour chaque intervalle, en remplaçant $\alpha^{\circ}$ par son angle d'occupation et $N$ par $50$, on trouve la valeur de l'effectif associé à cet intervalle.

Ainsi :

pour $\alpha^{\circ}=108^{\circ}$, on a : $n=\dfrac{108\times 50}{360}=15$

pour $\alpha^{\circ}=93.5^{\circ}$, on a : $n=\dfrac{93.5\times 50}{360}\simeq 13$

pour $\alpha^{\circ}=72.1^{\circ}$, on a : $n=\dfrac{72.1\times 50}{360}=10$

pour $\alpha^{\circ}=50.4^{\circ}$, on a : $n=\dfrac{50.4\times 50}{360}=7$

pour $\alpha^{\circ}=36^{\circ}$, on a : $n=\dfrac{36\times 50}{360}=5$

Donc, en ajoutant la ligne des effectifs dans le tableau statistique, on obtient :

\begin{array}{cccccc} Notes obtenues & [10; 12 [ & [12; 14 [ & [14; 16 [ & [16; 18 [ & [18; 20 [ \\ Montant de \\ la bourse & 10 000 & 15 000 & 20 000 & 25 000 & 30 000 \\ (F CFA) \\ Angles (en degrés) & 108 & 93.5 & 72.1 & 50.4 & 36 \\ Effectifs & 15 & 13 & 10 & 7 & 5 \end{array}

3) Calculons la valeur moyenne des bourses attribuées.

Soit $M$ la valeur moyenne des bourses attribuées alors, $M$ est donnée par :

M = \frac{total des "Produits"}{effectif total}

Donc, on a :

\begin{array}{rcl} M & = & \frac{15 \times 10 000 + 13 \times 15 000 + 10 \times 20 000 + 7 \times 25 000 + 5 \times 30 000}{50} \\ = & \frac{150 000 + 195 000 + 200 000 + 175 000 + 150 000}{50} \\ = & \frac{870 000}{50} \\ = & 17 400 \end{array}

Ainsi, la valeur moyenne des bourses attribuées est égale à $17\,400\;F\text{ CFA}.$

4) a) Déterminons le nombre d'élèves qui ont une note au moins égale à $12.$

Cela revient à déterminer le nombre d'élèves qui ont une note supérieure ou égale à $12.$

Dans le tableau statistique, en ajoutant la ligne des effectifs cumulés décroissants, on obtient :

\begin{array}{cccccc} Notes obtenues & [10; 12 [ & [12; 14 [ & [14; 16 [ & [16; 18 [ & [18; 20 [ \\ Montant de \\ la bourse & 10 000 & 15 000 & 20 000 & 25 000 & 30 000 \\ (F CFA) \\ Angles (en degrés) & 108 & 93.5 & 72.1 & 50.4 & 36 \\ Effectifs & 15 & 13 & 10 & 7 & 5 \\ E.C.D & 50 & 35 & 22 & 12 & 5 \end{array}

Alors, en suivant la ligne des $\text{E.C.D}$, on constate que $35$ élèves ont une note au moins égale à $12.$

En déduisons le pourcentage correspondant.

On a : $f=\dfrac{35}{50}\times 100=70$

Donc, $70\%$ des élèves ont une note au moins égale à $12.$

b) Déterminons le nombre d'élèves qui ont une bourse au plus égale à $25\,000\;F$

Cela revient à déterminer le nombre d'élèves qui ont une bourse inférieure ou égale à $25\,000\;F$

Dans le tableau statistique, en ajoutant la ligne des effectifs cumulés croissants, on obtient :

\begin{array}{cccccc} Notes obtenues & [10; 12 [ & [12; 14 [ & [14; 16 [ & [16; 18 [ & [18; 20 [ \\ Montant de \\ la bourse & 10 000 & 15 000 & 20 000 & 25 000 & 30 000 \\ (F CFA) \\ Angles (en degrés) & 108 & 93.5 & 72.1 & 50.4 & 36 \\ Effectifs & 15 & 13 & 10 & 7 & 5 \\ E.C.D & 50 & 35 & 22 & 12 & 5 \\ E.C.C & 15 & 28 & 38 & 45 & 50 \end{array}

Ainsi, d'après la ligne des $\text{E.C.C}$, on remarque que $45$ élèves ont une bourse au plus égale à $25\,000\;F.$

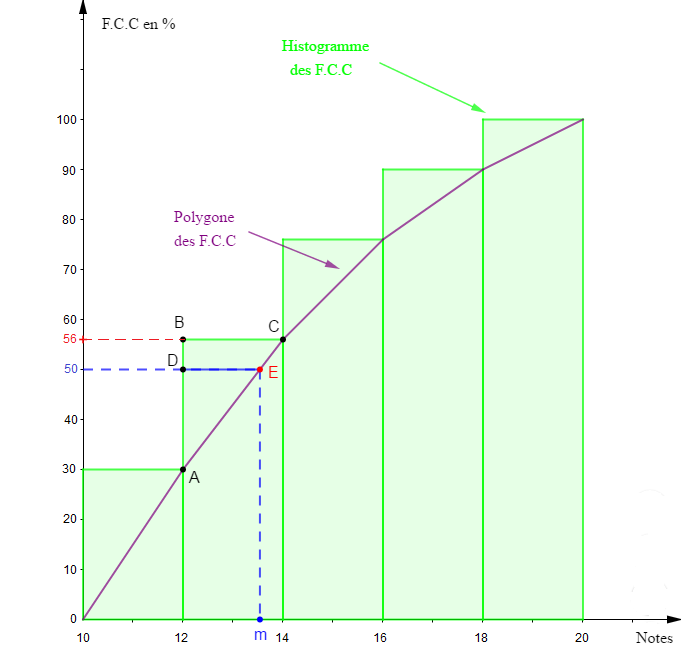
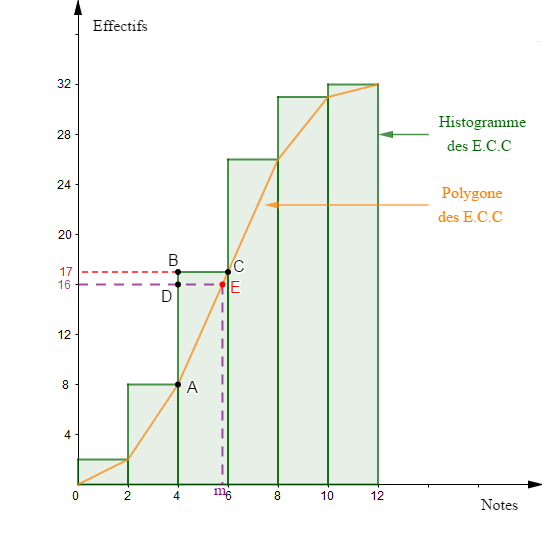
5) a) Construisons le polygone des fréquences cumulées croissantes.

Pour cela, exprimons les fréquences en pourcentages et ajoutons dans le tableau statistique les lignes des fréquences et des fréquences cumulées croissantes.

\begin{array}{cccccc} Notes obtenues & [10; 12 [ & [12; 14 [ & [14; 16 [ & [16; 18 [ & [18; 20 [ \\ Montant de \\ la bourse & 10 000 & 15 000 & 20 000 & 25 000 & 30 000 \\ (F CFA) \\ Angles (en degrés) & 108 & 93.5 & 72.1 & 50.4 & 36 \\ Effectifs & 15 & 13 & 10 & 7 & 5 \\ E.C.D & 50 & 35 & 22 & 12 & 5 \\ E.C.C & 15 & 28 & 38 & 45 & 50 \\ F en % & 30 & 26 & 20 & 14 & 10 \\ F.C.C en % & 30 & 56 & 76 & 90 & 100 \end{array}

\begin{array}{lrcl} Echelle : & 1 c m & ⟶ & 1 point \\ 1 c m & ⟶ & 10 % \end{array}

b) Déterminons la note médiane en utilisant le théorème de Thalès.

En effet, on sait que la médiane correspond à $50\%$ de l'effectif total.

Donc, pour déterminer la note médiane, on adopte la démarche suivante :

Sur l'axe des ordonnées, on place d'abord la valeur $50.$

Puis, on projette cette valeur sur le polygone des $F.C.C$ parallèlement à l'axe des abscisses.

On obtient le point $E.$

Ensuite, on projette le point $E$ sur l'axe des abscisse, parallèlement à l'axe des ordonnées.

On trouve alors $m$ qui représente la valeur médiane de cette série.

On constate que $m\in[12\;;\ 14[.$

Par ailleurs, les triangles $ABC\ $ et $\ ADE$ sont en position de Thalès. Donc, en appliquant le théorème de Thalès, on a :

\frac{D E}{B C} = \frac{A D}{A B}

En projetant $B\;,\ C\;,\ D\ $ et $\ E$ sur l'axe des abscisses, on trouve :

$DE=m-12$

$BC=14-12=2$

En projetant $A\;,\ B\ $ et $\ D$ sur l'axe des ordonnées, on trouve :

$AD=50-30=20$

$AB=56-30=26$

En reportant ces valeurs dans la relation précédente, on obtient :

\begin{array}{rcl} \frac{D E}{B C} = \frac{A D}{A B} & \Leftrightarrow & \frac{m - 12}{2} = \frac{20}{26} \\ \Leftrightarrow & 26 \times (m - 12) = 2 \times 20 \\ \Leftrightarrow & 26 m - 312 = 40 \\ \Leftrightarrow & 26 m = 40 + 312 \\ \Leftrightarrow & 26 m = 352 \\ \Leftrightarrow & m = \frac{352}{26} \\ \Leftrightarrow & m = 13.5 \end{array}

D'où, la note médiane est égale à $13.5$

Exercice 13

On a relevé les notes obtenues par des candidats à un examen noté sur $100$

\begin{array}{ccccccccc} Notes & 20 à 30 & 30 à 40 & 40 à 50 & 50 à 60 & 60 à 70 & 70 à 80 & 80 à 90 & 90 à 100 \\ Nombre \\ de & 3 & 6 & 9 & 12 & 18 & 6 & 3 & 3 \\ candidats \end{array}

1) Déterminons le nombre de candidats qui ont composé à cet examen.

Cela revient à calculer l'effectif total $N$ de la série.

Or, on sait que l'effectif total est égal à la somme des effectifs partiels.

Donc, on a : $N=3+6+9+12+18+6+3+3=60$

Ainsi, le nombre de candidats qui ont composé à cet examen est de $60.$

2) Donnons dans un même tableau les fréquences en $\%$, les fréquences cumulées croissantes et les fréquences cumulées décroissantes en $\%$

\begin{array}{ccccccccc} Notes & 20 à 30 & 30 à 40 & 40 à 50 & 50 à 60 & 60 à 70 & 70 à 80 & 80 à 90 & 90 à 100 \\ Nombre \\ de & 3 & 6 & 9 & 12 & 18 & 6 & 3 & 3 \\ candidats \\ F en % & 5 & 10 & 15 & 20 & 30 & 10 & 5 & 5 \\ F.C.C en % & 5 & 15 & 30 & 50 & 80 & 90 & 95 & 100 \\ F.C.D en % & 100 & 95 & 85 & 70 & 50 & 20 & 10 & 5 \end{array}

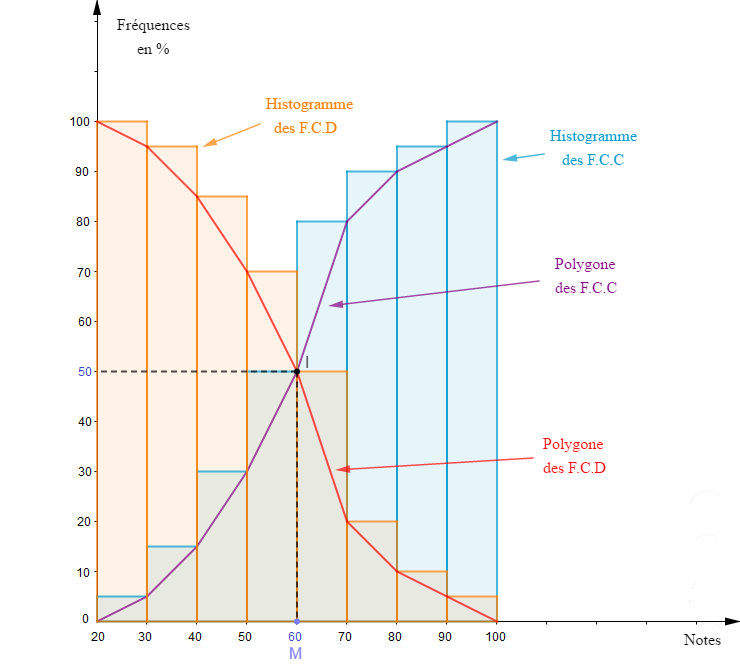
3) Représentons sur un même graphique le diagramme (polygone) des fréquences cumulées croissantes et décroissantes.

\begin{array}{lrcl} Echelle : & 1 c m & ⟶ & 10 points \\ 1 c m & ⟶ & 10 % \end{array}

4) Ces deux courbes se coupent en un point $I.$

Déterminons les coordonnées de $I.$

En projetant le point $I$ sur les axes du repère, on trouve :

I (60; 50)

5) On note $M$ l'abscisse du point $I.$

Déterminons le pourcentage de candidats ayant obtenu une note supérieure à $M.$

En effet, comme $M$ est l'abscisse de $I$ alors, $M=60.$

Or, en suivant la ligne des $\text{F.C.D}$, on remarque que le pourcentage de candidats ayant obtenu une note supérieure à $60$ est de $50\%.$

Par conséquent, $50\%$ des candidats ont obtenu une note supérieure à $M.$

$M$ représente alors la note médiane.

En effet, $M$ partage l'ensemble des candidats en deux groupes de même effectif :

$\cdot\ 50\%$ ayant obtenu une note supérieure à $M$

$\cdot\ 50\%$ ayant obtenu une note inférieure à $M$

D'où, $M$ est la note médiane.

Exercice 14

Un professeur de mathématiques a noté un devoir sur $10$ puis, a consigné les notes dans le tableau suivant :

\begin{array}{cccccccccccc} Notes & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\ Effectifs & 0 & 2 & 4 & 2 & 3 & 6 & 7 & 2 & 3 & 2 & 1 \end{array}

1) Calculons l'effectif total des élèves ayant composé puis la moyenne des notes obtenues.

On sait que l'effectif total $N$ des élèves ayant composé est égal à la somme des effectifs partiels.

Donc, on a :

N = 0 + 2 + 4 + 2 + 3 + 6 + 7 + 2 + 3 + 2 + 1 = 32

Ainsi, $32$ élèves ont eu à composer pour ce devoir.

Déterminons la moyenne des notes obtenues.

Soit $M$ la valeur moyenne des notes obtenues alors, $M$ est donnée par :

M = \frac{total des "Produits"}{effectif total}

Donc, on a :

\begin{array}{rcl} M & = & \frac{0 \times 0 + 2 \times 1 + 4 \times 2 + 2 \times 3 + 3 \times 4 + 6 \times 5 + 7 \times 6 + 2 \times 7 + 3 \times 8 + 2 \times 9 + 1 \times 10}{32} \\ = & \frac{0 + 2 + 8 + 6 + 12 + 30 + 42 + 14 + 24 + 18 + 10}{32} \\ = & \frac{166}{32} \\ ≃ & 5 \end{array}

Ainsi, la moyenne des notes obtenues est égale à $5.$

2) Le professeur répartit ensuite les notes en $6$ classes de notes pour obtenir une série classée.

a) Reprenons et complétons le tableau ci-dessous

\begin{array}{ccccccc} Classe \\ de & 0 \leq n < 2 & 2 \leq n < 4 & 4 \leq n < 6 & 6 \leq n < 8 & 8 \leq n < 10 & 10 \leq n < 12 \\ notes \\ Effectifs & 2 & 6 & 9 & 9 & 5 & 1 \\ E.C.C & 2 & 8 & 17 & 26 & 31 & 32 \end{array}

b) Représentons à l'aide d'un histogramme les effectifs cumulés croissants et traçons le polygone des effectifs cumulés croissants

\begin{array}{lrcl} Echelle : & 1 c m & ⟶ & 2 points \\ 1 c m & ⟶ & 4 élèves \end{array}

c) Définissons et déterminons la classe modale puis, calculons la médiane en utilisant le théorème de Thalès.

On appelle classe modale d'une série statistique, la classe qui a le plus grand effectif.

Dans cette série, il y a deux classes modales.

En effet, d'après le tableau statistique ci-dessus, on constate que les classes $4\leq n<6\ $ et $\ 6\leq n<8$ ont le même effectif et cet effectif est le plus grand.

Par conséquent, $4\leq n<6\ $ et $\ 6\leq n<8$ représentent les classes modales de la série.

Calculons la médiane de cette série en utilisant le théorème de Thalès.

En effet, on sait que la médiane correspond à la moitié de l'effectif total.

Or, l'effectif total $N=32$ donc, sa moitié $\dfrac{N}{2}=16.$

Alors, pour déterminer la note médiane, on procède comme suit :

Sur l'axe des ordonnées, on place d'abord la valeur $16.$

Puis, on projette cette valeur sur le polygone des $E.C.C$ parallèlement à l'axe des abscisses.

On obtient le point $E.$

Ensuite, on projette le point $E$ sur l'axe des abscisse, parallèlement à l'axe des ordonnées.

On trouve alors $m$ qui représente la valeur médiane de cette série.

On constate que $m\in[4\;;\ 6[.$

Par ailleurs, les triangles $ABC\ $ et $\ ADE$ sont en position de Thalès. Donc, en appliquant le théorème de Thalès, on obtient :

\frac{D E}{B C} = \frac{A D}{A B}

En projetant $B\;,\ C\;,\ D\ $ et $\ E$ sur l'axe des abscisses, on trouve :

$DE=m-4$

$BC=6-4=2$

En projetant $A\;,\ B\ $ et $\ D$ sur l'axe des ordonnées, on trouve :

$AD=16-8=8$

$AB=17-8=9$

En reportant ces valeurs dans la relation précédente, on obtient :

\begin{array}{rcl} \frac{D E}{B C} = \frac{A D}{A B} & \Leftrightarrow & \frac{m - 4}{2} = \frac{8}{9} \\ \Leftrightarrow & 9 \times (m - 4) = 2 \times 8 \\ \Leftrightarrow & 9 m - 36 = 16 \\ \Leftrightarrow & 9 m = 16 + 36 \\ \Leftrightarrow & 9 m = 52 \\ \Leftrightarrow & m = \frac{52}{9} \\ \Leftrightarrow & m = 5.7 \end{array}

D'où, la médiane de cette série est égale à $5.7$

d) Déterminons le nombre d'élèves qui ont une note au moins égale à $8.$

Cela revient à trouver le nombre d'élèves qui ont une note supérieure ou égale à $8.$

Ces élèves sont donc ceux des classes $8\leq n<10\ $ et $\ 10\leq n<12.$

Ainsi, d'après la ligne des effectifs, en faisant la somme des effectifs de ces deux classes, on trouve :

5 + 1 = 6

D'où, $6$ élèves ont une note au moins égale à $8.$

e) Déterminons le pourcentage d'élèves qui ont moins de $6.$

D'après la ligne des $\text{E.C.C}$, on a $17$ élèves qui ont de $6.$

Cela correspond, en terme de pourcentage, à :

f = \frac{17}{32} \times 100 ≃ 53

Donc, $53\%$ des élèves ont moins de $6.$

f) Donnons la signification de l'effectif cumulé croissant associé à la classe $6\leq n<8.$

En effet, d'après la ligne des $\text{E.C.C}$, le nombre $26$ correspond à la classe $6\leq n<8.$

Cela signifie que $26$ élèves ont une note strictement inférieure à $8.$

Donc, l'effectif cumulé croissant associé à la classe $6\leq n<8$ représente le nombre d'élèves qui ont une note strictement inférieure à $8.$

Exercice 15

Pour chacun des énoncés ci-dessous, $3$ réponses $R_{1}\;,\ R_{2}\;,\ R_{3}$ sont proposées.

Pour chaque énoncé relevons le numéro suivi de la réponse choisie.

On considère la série de notes d'élèves représentée ci-dessous

\begin{array}{ccccc} Note & 1 à 4 & 5 à 9 & 10 à 14 & 15 à 20 \\ Effectif & 0 & 9 & 10 & 6 \end{array}

\begin{array}{ccc} N^{\circ} Enoncé & Réponse \\ 1 & ⟹ & R_{2} \\ 2) a) & ⟹ & R_{3} \\ 2) b) & ⟹ & R_{1} \\ 2) c) & ⟹ & R_{3} \end{array}

Ce qui peut encore s'écrire :

1) Le centre de la classe $[22\;;\ 30]$ est : $26$

2) a) Le pourcentage d'élèves dont les notes varient de $5$ à $9$ est : $36\%$

2) b) La note moyenne de la série est : $11.52$

2) c) La classe modale de la série est : $10$ à $14$

Exercice 16

Déterminons la médiane et les quartiles de la série :

1; 1; 3; 5; 5; 6; 8; 8; 8; 10; 11

On obtient alors :

1; 1; \underset{1^{e} quartile}{\underset{⏟}{3}}; 5; 5; \underset{médiane}{\underset{⏟}{6}}; 8; 8; \underset{3^{e} quartile}{\underset{⏟}{8}}; 10; 11

En effet, dans cette série déjà ordonnée, nous remarquons que l'effectif total est égal : $N=11.$

C'est un nombre impair.

Donc, la position de la médiane est donnée par :

\frac{N + 1}{2} = \frac{11 + 1}{2} = \frac{12}{2} = 6

Ce qui signifie que la médiane est déterminée par la $6^{e}$ valeur de la série.

Ce qui correspond à : $6$

La position du premier quartile $Q_{1}$ qui correspond au quart de l'effectif total est donnée par :

\frac{N + 1}{4} = \frac{11 + 1}{4} = \frac{12}{4} = 3

Donc, le premier quartile $Q_{1}$ est déterminé par la $3^{e}$ valeur de la série.

Ce qui correspond à : $3$

La position du troisième quartile $Q_{3}$ qui correspond aux $\dfrac{3}{4}$ de l'effectif total est donnée par :

\frac{3 (N + 1)}{4} = \frac{3 (11 + 1)}{4} = \frac{36}{4} = 9

Ainsi, le troisième quartile $Q_{3}$ est déterminé par la $9^{e}$ valeur de la série.

Ce qui correspond à : $8$

Autre méthode

Dans cette série déjà ordonnée, l'effectif total donné par $N=11$ est un nombre impair.

Donc, la position de la médiane est donnée par :

\frac{N + 1}{2} = \frac{11 + 1}{2} = \frac{12}{2} = 6

Ainsi, la médiane est déterminée par la $6^{e}$ valeur de la série.

Ce qui correspond à : $6$

Par suite, cette médiane partage la série en deux parties de même effectif :

$1^{e}\text{ partie}\ :\ 1\;;\ 1\ ;\ 3\;;\ 5\;;\ 5$

$2^{e}\text{ partie}\ :\ 8\;;\ 8\;;\ 8\;;\ 10\;;\ 11$

Le premier quartile qui correspond au quart de l'effectif total est donc représenté par la valeur de la série qui partage la première partie en deux parts de même effectif.

Ainsi, le premier quartile est égal à : $3$

C'est la $3^{e}$ valeur de la série, dans l'ordre du décompte.

Le troisième quartile qui correspond aux $\dfrac{3}{4}$ de l'effectif total est représenté par la valeur de la série qui partage la deuxième partie en deux groupes de même effectif.

Donc, le troisième quartile est égal à : $8$

C'est la $9^{e}$ valeur de la série, dans l'ordre du décompte.

Exercice 17

Le tableau suivant donne la répartition des notes des élèves de $3^{\text{ème}}$ à un devoir de biologie.

\begin{array}{cccccc} Classes & [0; 4 [ & [4; 8 [ & [8; 12 [ & [12; 16 [ & [16; 20 [ \\ Effectifs & 3 & 5 & 9 & 7 & 4 \end{array}

1) Déterminons la classe modale et une approximation de la moyenne de la classe à ce devoir.

On rappelle que classe modale d'une série statistique est la classe qui a le plus grand effectif.

D'après le tableau statistique ci-dessus, on constate que la classe $[8\;;\ 12[$ a le plus grand effectif.

Par conséquent, elle représente la classe modale de la série.

Déterminons une approximation de la moyenne.

Comme la série est groupée en classes alors, nous allons utiliser les centres de ces classes pour calculer la moyenne.

Les centres sont donnés dans le tableau ci-dessous.

\begin{array}{cccccc} Classes & [0; 4 [ & [4; 8 [ & [8; 12 [ & [12; 16 [ & [16; 20 [ \\ Centres & 2 & 6 & 10 & 14 & 18 \\ Effectifs & 3 & 5 & 9 & 7 & 4 \end{array}

Soit $M$ la note moyenne alors, on a :

M = \frac{total des "Produits"}{effectif total}

Or, l'effectif total $N$ qui est égal à la somme des effectifs partiels, est donné par :

N = 3 + 5 + 9 + 7 + 4 = 28

Donc, on obtient :

\begin{array}{rcl} M & = & \frac{3 \times 2 + 5 \times 6 + 9 \times 10 + 7 \times 14 + 4 \times 18}{28} \\ = & \frac{6 + 30 + 90 + 98 + 72}{28} \\ = & \frac{296}{28} \\ = & 10.57 \end{array}

Ainsi, la moyenne de la classe à ce devoir est approximativement égale à $10.5$

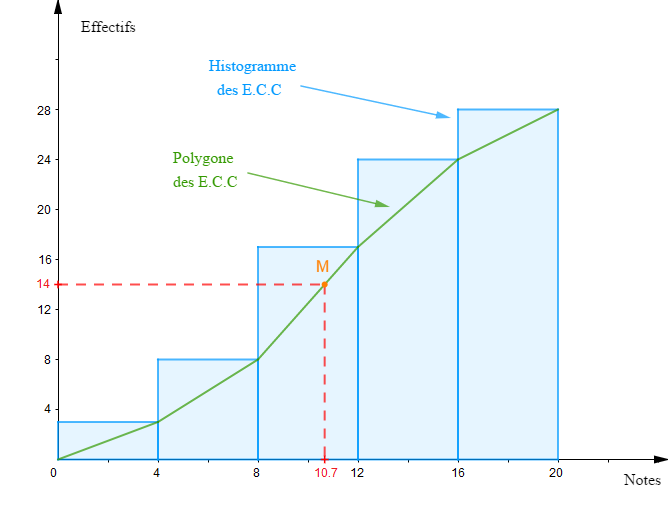
2) Calculons la médiane de cette série.

Comme la série est groupée en classes alors, nous allons utiliser le polygone des effectifs cumulés croissants pour déterminer la médiane.

En ajoutant la ligne des $\text{E.C.C}$ au tableau statistique, on obtient :

\begin{array}{cccccc} Classes & [0; 4 [ & [4; 8 [ & [8; 12 [ & [12; 16 [ & [16; 20 [ \\ Centres & 2 & 6 & 10 & 14 & 18 \\ Effectifs & 3 & 5 & 9 & 7 & 4 \\ E.C.C & 3 & 8 & 17 & 24 & 28 \end{array}

En construisant l'histogramme des $\text{E.C.C}$ puis, le polygone des $\text{E.C.C}$, on obtient :

\begin{array}{lrcl} Echelle : & 1 c m & ⟶ & 2 points \\ 1 c m & ⟶ & 4 élèves \end{array}

Comme l'effectif total $N=28$ est un nombre pair alors, la position qui détermine la valeur médiane de cette série est donnée par :

\frac{N}{2} = \frac{28}{2} = 14

Donc, la note du $14^{e}$ élève, dans l'ordre du décompte, représente la note médiane de cette série.

Pour déterminer cette valeur médiane, on procède comme suit :

Sur l'axe des ordonnées, on place d'abord la valeur $14.$

Puis, on projette cette valeur sur le polygone des $\text{E.C.C}$ parallèlement à l'axe des abscisses.

On obtient le point $M.$

Ensuite, on projette le point $M$ sur l'axe des abscisse, parallèlement à l'axe des ordonnées.

On trouve alors la valeur $10.7$

Cela signifie que $10.7$ est la note du $14^{e}$ élève, dans l'ordre du décompte.

Par conséquent, la médiane de cette série est égale à $10.7$

3) Construisons l'histogramme des effectifs.

\begin{array}{lrcl} Echelle : & 1 c m & ⟶ & 2 points \\ 1 c m & ⟶ & 1 élève \end{array}

$\text{Histogramme des effectifs}$

Exercice 18

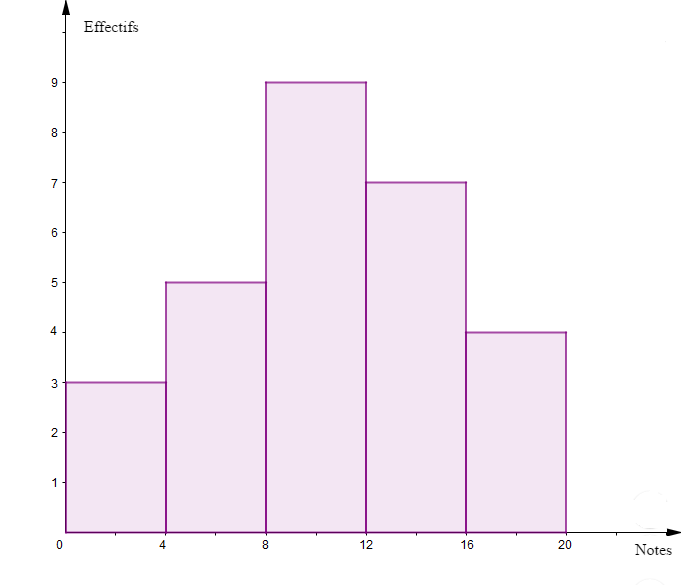
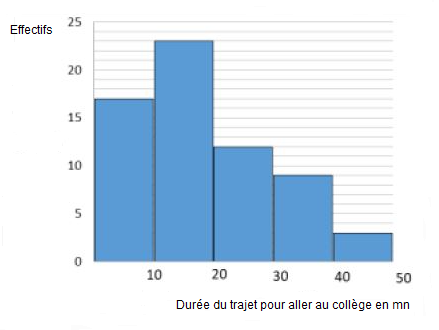
1) A partir de l'histogramme ci-dessous, donnons le tableau des effectifs par classe de la série statistique représentée

En effet, l'effectif de chaque classe est déterminé par la hauteur de la bande correspondante.

Donc, sur l'axe des ordonnées, la valeur qui coïncide avec cette hauteur représente l'effectif de la classe considérée.

On obtient alors le tableau suivant :

\begin{array}{cccccc} Classes & [0; 10 [ & [10; 20 [ & [20; 30 [ & [30; 40 [ & [40; 50 [ \\ Effectifs & 17 & 23 & 12 & 9 & 3 \end{array}

2) Calculons l'effectif total de cette série.

L'effectif total $N$ est égal à la somme des effectifs partiels.

Alors, on a :

N = 17 + 23 + 12 + 9 + 3 = 64

3) Déterminons une approximation de la moyenne de cette série.

Comme la série est groupée en classes alors, nous allons utiliser les centres de ces classes pour calculer la moyenne.

Les centres sont donnés dans le tableau ci-dessous.

\begin{array}{cccccc} Classes & [0; 10 [ & [10; 20 [ & [20; 30 [ & [30; 40 [ & [40; 50 [ \\ Centres & 5 & 15 & 25 & 35 & 45 \\ Effectifs & 17 & 23 & 12 & 9 & 3 \end{array}

Soit $M$ la moyenne de cette série alors, on a :

M = \frac{total des "Produits"}{effectif total}

Ce qui donne :

\begin{array}{rcl} M & = & \frac{17 \times 5 + 23 \times 15 + 12 \times 25 + 9 \times 35 + 3 \times 45}{64} \\ = & \frac{85 + 345 + 300 + 315 + 135}{64} \\ = & \frac{1 180}{64} \\ = & 18.43 \end{array}

Ainsi, la moyenne de cette série est approximativement égale à $18\;mn.$

4) Déterminons graphiquement la classe modale.

On rappelle que classe modale d'une série statistique est la classe qui a le plus grand effectif.

Sur le l'histogramme des effectifs, cette classe modale est représentée par la bande de plus grande hauteur.

C'est donc la classe $[10\;;\ 20[$

Exercice 19

La taille moyenne des onze joueurs d'une équipe de football est de $1.81$ mètre.

On a pu relever la taille, en mètre, des dix joueurs sauf celle du gardien de but :

1.71 - 1.80 - 1.85 - 1.75 - 1.78 - 1.83 - 1.75 - 1.80 - 1.85 - 1.90

1) Déterminons la taille du gardien.

Soit $x$ la taille du gardien et $N=11$ l'effectif total de l'équipe.

Alors, la taille moyenne $M$ de cette équipe est donnée par :

M = \frac{total des tailles des joueurs}{effectif total}

\begin{array}{rcl} M & = & \frac{x + 1.71 + 1.80 + 1.85 + 1.75 + 1.78 + 1.83 + 1.75 + 1.80 + 1.85 + 1.90}{11} \\ = & \frac{x + 18.02}{11} \end{array}

Or, on sait que la taille moyenne $M$ des onze joueurs est de $1.81$ mètre.

Donc, on a : $\dfrac{x+18.02}{11}=1.81$

En résolvant cette équation, on trouve la valeur de $x$ qui détermine la taille du gardien de but.

Soit alors :

\begin{array}{rcl} \frac{x + 18.02}{11} = 1.81 & \Leftrightarrow & x + 18.02 = 1.81 \times 11 \\ \Leftrightarrow & x + 18.02 = 19.91 \\ \Leftrightarrow & x = 19.91 - 18.02 \\ \Leftrightarrow & x = 1.89 \end{array}

Ainsi, la taille du gardien est de : $1.89\;m$

2) Déterminons la taille médiane de ces onze joueurs.

Pour cela, nous allons commencer par ordonner la série des tailles des onze joueurs.

Alors, dans l'ordre croissant, on a :

1.71 - 1.75 - 1.75 - 1.78 - 1.80 - 1.80 - 1.83 - 1.85 - 1.85 - 1.89 - 1.90

Comme l'effectif total de l'équipe $N$ est un nombre impair alors, la position de la médiane est donnée par :

\frac{N + 1}{2} = \frac{11 + 1}{2} = \frac{12}{2} = 6

Donc, dans l'ordre du décompte, la médiane est déterminée par la $6^{e}$ valeur de la série.

Ce qui correspond à : $1.80$

Ainsi, la taille médiane de ces onze joueurs est de : $1.80\;m$

3) Dans cette équipe, il y a trois remplaçants de la même taille.

La moyenne de la taille de ces quatorze joueurs est alors de $1.84$ mètre.

4) Déterminons la taille de chacun des trois remplaçants.

Comme trois remplaçants de la même taille alors, appelons $y$ la taille de chacun des remplaçants.

L'effectif total de l'équipe étant $N=14$ donc, la taille moyenne est donnée par :

\begin{array}{rcl} M & = & \frac{3 y + 1.89 + 1.71 + 1.80 + 1.85 + 1.75 + 1.78 + 1.83 + 1.75 + 1.80 + 1.85 + 1.90}{14} \\ = & \frac{3 y + 19.91}{14} \end{array}

Or, on sait que la taille moyenne $M$ des quatorze joueurs de l'équipe est de $1.84$ mètre.

Ce qui se traduit alors par : $\dfrac{3y+19.91}{14}=1.84$

En résolvant cette équation, on trouve la valeur de $y$ qui détermine la taille de chacun des trois remplaçants.

On a :

\begin{array}{rcl} \frac{3 y + 19.91}{14} = 1.84 & \Leftrightarrow & 3 y + 19.91 = 1.84 \times 14 \\ \Leftrightarrow & 3 y + 19.91 = 25.76 \\ \Leftrightarrow & 3 y = 25.76 - 19.91 \\ \Leftrightarrow & 3 y = 5.85 \\ \Leftrightarrow & y = \frac{5.85}{3} \\ \Leftrightarrow & y = 1.95 \end{array}

Ainsi, la taille de chacun des trois remplaçants est de : $1.95\;m$

5) Déterminons la taille médiane de cette nouvelle série.

En réordonnant cette nouvelle série, on obtient :

1.71 - 1.75 - 1.75 - 1.78 - 1.80 - 1.80 - 1.83 - 1.85 - 1.85 - 1.89 - 1.90 - 1.95 - 1.95 - 1.95

Comme l'effectif $N=14$ est un nombre pair alors, la moitié est :

\frac{N}{2} = \frac{14}{2} = 7

Donc, la valeur de la médiane $m$ est donnée par :

m = \frac{7^{e} valeur de la série + 8^{e} valeur de la série}{2}

Or, dans l'ordre du décompte, la $7^{e}$ valeur est égale à $1.83$ et la $8^{e}$ valeur est de $1.85$

Ainsi, on a :

\begin{array}{rcl} m & = & \frac{1.83 + 1.85}{2} \\ = & \frac{3.68}{2} \\ = & 1.84 \end{array}

D'où, la taille médiane de cette nouvelle série est de : $1.84\;m$

Exercice 20

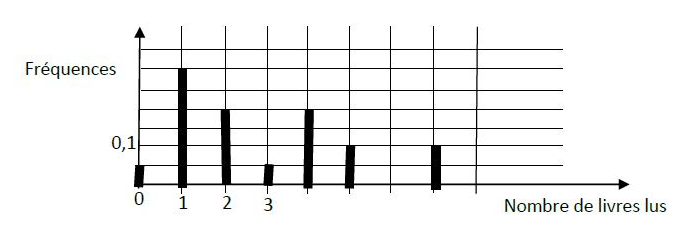
Une enquête a été réalisée dans une bibliothèque pour étudier le nombre de livres lus par les usagers, en décembre $2015.$

Le diagramme en bâtons ci-dessous donne la fréquence associée à chaque nombre de livres lus.

1) Déterminons graphiquement le nombre médian de livres lus.

Le nombre médian de livres lus est égal à $2.$

Expliquons notre démarche.

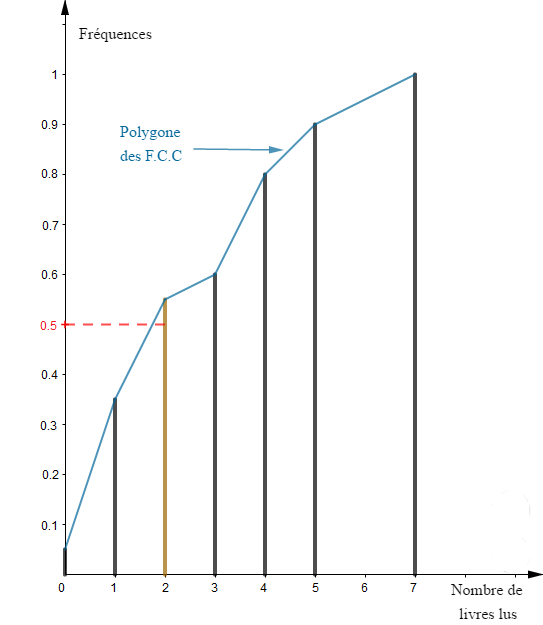
En effet, en partant du diagramme en bâtons ci-dessus, nous construisons le diagramme des fréquences cumulées croissantes puis, nous traçons le polygone des $\text{F.C.C}.$

Alors, la médiane de cette série correspond à $50\%$ des effectifs.

Ainsi, pour déterminer le nombre médian de livres lus, on adopte la démarche suivante :

Sur l'axe des ordonnées, on place d'abord la valeur $0.5$ qui est équivalent à $50\%$ des effectifs.

Puis, on projette cette valeur sur le polygone des $\text{F.C.C}$ parallèlement à l'axe des abscisses.

Ensuite, en suivant cette ligne de projection, on croise le diagramme en bâtons correspondant à : $2$ livres lus.

Cette valeur représente donc la médiane.

D'où, le nombre médian de livres lus est égal à $2.$

$\text{Diagramme des fréquences cumulées croissantes}$

2) Calculons le nombre moyen de livres lus par les usagers de cette bibliothèque en décembre $2015.$

Soit $M$ le nombre moyen de livres lus par les usagers alors, $M$ est donnée par :

M = \frac{total des "Produits"}{effectif total}

Soit $N$ l'effectif total et soient :

$\ast\ \ n_{1}\;,\ n_{2}\;,\ n_{3}\;,\ n_{4}\;,\ n_{5}\;,\ n_{6}\ $ et $\ n_{7}$ les effectifs partiels respectifs des modalités.

$\ast\ \ f_{1}\;,\ f_{2}\;,\ f_{3}\;,\ f_{4}\;,\ f_{5}\;,\ f_{6}\ $ et $\ f_{7}$ les fréquences respectives associées.

Alors, on a :

\begin{array}{rcl} M & = & \frac{n_{1} \times 0 + n_{2} \times 1 + n_{3} \times 2 + n_{4} \times 3 + n_{5} \times 4 + n_{6} \times 5 + n_{7} \times 7}{N} \\ = & \frac{n_{1}}{N} \times 0 + \frac{n_{2}}{N} \times 1 + \frac{n_{3}}{N} \times 2 + \frac{n_{4}}{N} \times 3 + \frac{n_{5}}{N} \times 4 + \frac{n_{6}}{N} \times 5 + \frac{n_{7}}{N} \times 7 \\ = & f_{1} \times 0 + f_{2} \times 1 + f_{3} \times 2 + f_{4} \times 3 + f_{5} \times 4 + f_{6} \times 5 + f_{7} \times 7 \\ = & 0.05 \times 0 + 0.3 \times 1 + 0.2 \times 2 + 0.05 \times 3 + 0.2 \times 4 + 0.1 \times 5 + 0.1 \times 7 \\ = & 0 + 0.3 + 0.4 + 0.15 + 0.8 + 0.5 + 0.7 \\ ≃ & 3 \end{array}

Donc, le nombre moyen de livres lus par les usagers de cette bibliothèque en décembre $2015$ est égal à $3.$

Exercice 21

Reproduisons puis répondons par Vrai ou Faux à chacune des affirmations ci-dessous.

\begin{array}{lc} Affirmations & Réponses \\ 1) La médiane d'une série statistique est forcément & Faux \\ une des valeurs de la série. \\ 2) Dans un regroupement par classe, une valeur & Faux \\ peut appartenir à deux classes différentes. \\ 3) Dans une série statistique, la moitié des données & Faux \\ ont une valeur inférieure à la moyenne. \end{array}

Exercice 22

La distribution des salaires mensuels des $530$ ouvriers d'une entreprise est représentée par le tableau ci-dessous.

\begin{array}{ccccccc} Salaires \\ en & [45 000; 47 000 [ & [47 000; 49 000 [ & [49 000; 51 000 [ & [51 000; 53 000 [ & [53 000; 55 000 [ & [55 000; 57 000 [ \\ F CFA \\ Effectifs \\ Effectifs \\ cumulés \\ croissants \\ Fréquence en % \\ Angles \\ correspondant & 17^{\circ} & 75^{\circ} & 122^{\circ} & 85^{\circ} & 34^{\circ} & 27^{\circ} \\ aux fréquences \end{array}

1) Reproduisons et complétons le tableau ci-dessus.

En effet, l'angle d'occupation correspondant aux fréquences est équivalent à l'angle d'occupation de chaque intervalle.

Or, on sait que l'angle d'occupation $\alpha^{\circ}$ de chaque intervalle vérifie :

α^{\circ} = \frac{360^{\circ} \times n}{N}

où, $n$ est l'effectif partiel et $N$ l'effectif total représenté par le nombre total d'ouvriers.

Donc, l'effectif partiel $n$ associé à chaque intervalle est donné par :

n = \frac{α^{\circ} \times N}{360^{\circ}}

Alors, pour chaque intervalle, en remplaçant $\alpha^{\circ}$ par son angle d'occupation et $N$ par $530$, on trouve la valeur de l'effectif associé à cet intervalle.

Ainsi :

pour $\alpha^{\circ}=17^{\circ}$, on a : $n=\dfrac{17\times 530}{360}=25$

pour $\alpha^{\circ}=75^{\circ}$, on a : $n=\dfrac{75\times 530}{360}=110$

pour $\alpha^{\circ}=122^{\circ}$, on a : $n=\dfrac{122\times 530}{360}\simeq 180$

pour $\alpha^{\circ}=85^{\circ}$, on a : $n=\dfrac{85\times 530}{360}=125$

pour $\alpha^{\circ}=34^{\circ}$, on a : $n=\dfrac{34\times 530}{360}=50$

pour $\alpha^{\circ}=27^{\circ}$, on a : $n=\dfrac{27\times 530}{360}\simeq 40$

Par ailleurs, pour calculer la fréquence $f$, en pourcentage, d'un intervalle, on utilise la formule suivante :

f = \frac{n}{N} \times 100

où, $n$ est l'effectif partiel et $N$ l'effectif total

Donc, en ajoutant la ligne des effectifs, la ligne des $\text{E.C.C}$ et la ligne des fréquences dans le tableau statistique, on obtient :

\begin{array}{ccccccc} Salaires \\ en & [45 000; 47 000 [ & [47 000; 49 000 [ & [49 000; 51 000 [ & [51 000; 53 000 [ & [53 000; 55 000 [ & [55 000; 57 000 [ \\ F CFA \\ Effectifs & 25 & 110 & 180 & 125 & 50 & 40 \\ E.C.C & 25 & 135 & 315 & 440 & 490 & 530 \\ Fréquence en % & 5 & 21 & 34 & 23.5 & 9 & 7.5 \\ Angles \\ correspondant & 17^{\circ} & 75^{\circ} & 122^{\circ} & 85^{\circ} & 34^{\circ} & 27^{\circ} \\ aux fréquences \end{array}

2) Déterminons le nombre d'ouvriers ayant un salaire strictement inférieur à $51\,000\;F$

En suivant la ligne des $\text{E.C.C}$, nous constatons que $315$ ouvriers ont un salaire strictement inférieur à $51\,000\;F$

3) Calculons le salaire moyen de cette entreprise.

Comme la série est groupée en classes alors, nous allons utiliser les centres de ces classes pour calculer la moyenne.

En ajoutant la ligne des centres dans le tableau statistique, on obtient :

\begin{array}{ccccccc} Salaires \\ en & [45 000; 47 000 [ & [47 000; 49 000 [ & [49 000; 51 000 [ & [51 000; 53 000 [ & [53 000; 55 000 [ & [55 000; 57 000 [ \\ F CFA \\ Centres & 46 000 & 48 000 & 50 000 & 52 000 & 54 000 & 56 000 \\ Effectifs & 25 & 110 & 180 & 125 & 50 & 40 \\ E.C.C & 25 & 135 & 315 & 440 & 490 & 530 \\ Fréquence en % & 5 & 21 & 34 & 23.5 & 9 & 7.5 \\ Angles \\ correspondant & 17^{\circ} & 75^{\circ} & 122^{\circ} & 85^{\circ} & 34^{\circ} & 27^{\circ} \\ aux fréquences \end{array}

Soit $M$ le salaire moyen de cette entreprise alors, on a :

M = \frac{total des "Produits"}{effectif total}

Ce qui donne :

\begin{array}{rcl} M & = & \frac{25 \times 46 000 + 110 \times 48 000 + 180 \times 50 000 + 125 \times 52 000 + 50 \times 54 000 + 40 \times 56 000}{530} \\ = & \frac{1 150 000 + 5 280 000 + 9 000 000 + 6 500 000 + 2 700 000 + 2 240 000}{530} \\ = & \frac{26 870 000}{530} \\ = & 50 698 \end{array}

Ainsi, le salaire moyen de cette entreprise est égal à $50\,698\;F.$

Exercice 23

On a réparti $100$ personnes selon leur temps de sieste exprimé en minutes $(mn).$

\begin{array}{cccccc} Classes & [30; 50 [ & [50; 70 [ & [70; 90 [ & [90; 110 [ & [110; 130 [ \\ Effectifs & 10 & 20 & x & 40 & y \end{array}

Le temps moyen de sieste est de $82\;mn.$

1) Reproduisons puis complétons le tableau ci-dessus en mettant les centres de classes.

\begin{array}{lccccc} Classes & [30; 50 [ & [50; 70 [ & [70; 90 [ & [90; 110 [ & [110; 130 [ \\ Effectifs & 10 & 20 & x & 40 & y \\ Centres & 40 & 60 & 80 & 100 & 120 \end{array}

2) En exprimant l'effectif total et la moyenne en fonction de $x\ $ et $\ y$, montrons que $x\ $ et $\ y$ vérifient le système suivant :

{\begin{array}{rcl} x + y & = & 30 \\ 2 x + 3 y & = & 65 \end{array}

Soit $N$ l'effectif total alors, on a :

N = 10 + 20 + x + 40 + y

Comme $N=100$ alors,

\begin{array}{rcl} 10 + 20 + x + 40 + y = 100 & \Rightarrow & 70 + x + y = 100 \\ \Rightarrow & x + y = 100 - 40 \\ \Rightarrow & x + y = 30 \end{array}

Donc, $x\ $ et $\ y$ vérifient l'équation suivante :

x + y = 30 (1)

Par ailleurs, le temps moyen de sieste $M$ est de $82\;mn.$

Or, en appelant :

$\ast\ \ C_{1}\;,\ C_{2}\;,\ C_{3}\;;\ C_{4}$ et $\ C_{5}$ les centres respectifs des classes.

$\ast\ \ n_{1}\;,\ n_{2}\;,\ n_{3}\;;\ n_{4}$ et $\ n_{5}$ les effectifs partiels respectifs et $N$ l'effectif total.

On obtient :

M = \frac{n_{1} \times C_{1} + n_{2} \times C_{2} + n_{3} \times C_{3} + n_{4} \times C_{4} + n_{5} \times C_{5}}{N}

Par suite, $\dfrac{10\times 40+20\times 60+x\times 80+40\times 100+y\times 120}{100}=82$

Après calcul, on obtient :

\frac{400 + 1200 + 80 x + 4000 + 120 y}{100} = 82

Ce qui donne :

\begin{array}{rcl} \frac{5600 + 80 x + 120 y}{100} = 82 & \Rightarrow & \frac{560 + 8 x + 12 y}{10} = 82 \\ \Rightarrow & 560 + 8 x + 120 y = 82 \times 10 \\ \Rightarrow & 560 + 8 x + 12 y = 820 \\ \Rightarrow & 8 x + 12 y = 820 - 560 \\ \Rightarrow & 8 x + 12 y = 260 \\ \Rightarrow & 4 \times (2 x + 3 y) = 4 \times 65 \\ \Rightarrow & 2 x + 3 y = 65 \end{array}

Ainsi, $x\ $ et $\ y$ vérifient aussi l'équation suivante :

2 x + 3 y = 65 (2)

Par conséquent, $x\ $ et $\ y$ vérifient le système d'équations suivant, formé des équations (1) et (2) :

{\begin{array}{rcl} x + y & = & 30 \\ 2 x + 3 y & = & 65 \end{array}

3) Pour la suite, on donne $x=25\ $ et $\ y=5.$

a) Reprenons le tableau ci-dessus en indiquant les fréquences en $(\%)$ et les fréquences cumulées croissantes en $(\%).$

\begin{array}{lccccc} Classes & [30; 50 [ & [50; 70 [ & [70; 90 [ & [90; 110 [ & [110; 130 [ \\ Effectifs & 10 & 20 & 25 & 40 & 5 \\ Centres & 40 & 60 & 80 & 100 & 120 \\ F en % & 10 & 20 & 25 & 40 & 15 \\ F.C.C en % & 10 & 30 & 55 & 95 & 100 \end{array}

b) Déterminons le pourcentage $f$ de personnes qui ont un temps de sieste au moins égal à $70\;mn.$

Cela correspond au nombre de personnes qui ont un temps de sieste supérieur ou égal à $70\;mn.$

En suivant la ligne des fréquences, on obtient :

f = 25 + 40 + 15 = 70

Donc, $70\%$ de personnes ont un temps de sieste au moins égal à $70\;mn.$

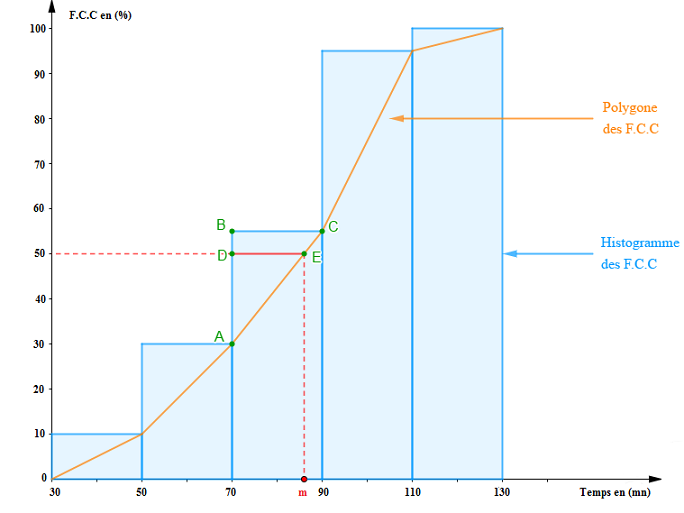
4) Traçons l'histogramme et le polygone des fréquences cumulées croissantes en $(\%).$

\begin{array}{rcl} Échelle : 1 c m & ⟶ & 10 m n \\ 1 c m & ⟶ & 10 % \end{array}

5) A l'aide du théorème de Thalès, déterminons le temps médian de sieste.

Soit $m$ le temps médian de sieste alors, $m$ correspond à $50\%$ de l'effectif total.

En projetant, on constate que $m\in[70\;;\ 90[.$

Par ailleurs, les triangles $ABC\ $ et $\ ADE$ sont en position de Thalès. Donc, en appliquant le théorème de Thalès, on a :

\frac{D E}{B C} = \frac{A D}{A B}

Pour calculer ces distances, on utilise une démarche plus simple.

Ainsi, comme $D\ $ et $\ E$ d'une part, et $B\ $ et $\ C$ d'autre part, ont même ordonnée alors, en projetant sur l'axe des abscisses, on trouve :

$DE=m-70$

$BC=90-70=20$

De la même manière, comme $A\;,\ B\ $ et $\ D$ ont même abscisse alors, en projetant sur l'axe des ordonnées, on obtient :

$AD=50-30=20$

$AB=55-30=25$

En reportant ces valeurs dans la relation précédente, on trouve :

\begin{array}{rcl} \frac{D E}{B C} = \frac{A D}{A B} & \Leftrightarrow & \frac{m - 70}{20} = \frac{20}{25} \\ \Leftrightarrow & 25 \times (m - 70) = 20 \times 20 \\ \Leftrightarrow & 25 m - 1 750 = 400 \\ \Leftrightarrow & 25 m = 400 + 1 750 \\ \Leftrightarrow & 25 m = 2 150 \\ \Leftrightarrow & m = \frac{2 150}{25} \\ \Leftrightarrow & m = 86 \end{array}

D'où, le temps médian de sieste est égal à $86\;mn$

Exercice de synthèse

I. Les notes des $160$ candidats à un concours sont consignées dans le tableau suivant

\begin{array}{cccccc} Notes & [10; 12 [ & [12; 14 [ & [14; 16 [ & [16; 18 [ & [18; 20 [ \\ Nombres \\ de & 48 & 40 & x & 24 & y \\ candidats \end{array}

La moyenne de cette série statistique est égale à $14$ et la somme de $x\ $ et $\ y$ est égale à $48.$

1) Le caractère étudié est la note de chaque candidat.

Déterminons sa nature.

En effet, la note étant une grandeur mesurable donc, ce caractère est de nature quantitative.

2) Calculons et plaçons dans le tableau, le centre de chaque classe.

Les centres sont alors donnés dans le tableaux suivant :

\begin{array}{cccccc} Notes & [10; 12 [ & [12; 14 [ & [14; 16 [ & [16; 18 [ & [18; 20 [ \\ Nombres \\ de & 48 & 40 & x & 24 & y \\ candidats \\ Centres & 11 & 13 & 15 & 17 & 19 \end{array}

3) Déterminons $x\ $ et $\ y$

En effet, on sait que la somme de $x\ $ et $\ y$ est égale à $48.$

Ce qui se traduit alors par :

x + y = 48 (1)

On sait que :

M = \frac{total des "Produits"}{effectif total}

Alors, on a :

\begin{array}{rcl} M & = & \frac{48 \times 11 + 40 \times 13 + x \times 15 + 24 \times 17 + y \times 19}{160} \\ = & \frac{528 + 520 + 15 x + 408 + 19 y}{160} \\ = & \frac{15 x + 19 y + 1 456}{160} \end{array}

Donc, $\boxed{M=\dfrac{15x+19y+1\,456}{160}}$

Or, on sait que la moyenne de cette série est de $14$ ; ce qui signifie que :

M = \frac{15 x + 19 y + 1 456}{160} = 14

Par suite, en calculant, on trouve :

\begin{array}{rcl} \frac{15 x + 19 y + 1 456}{160} = 14 & \Leftrightarrow & 15 x + 19 y + 1 456 = 14 \times 160 \\ \Leftrightarrow & 15 x + 19 y + 1 456 = 2 240 \\ \Leftrightarrow & 15 x + 19 y = 2 240 - 1 456 \\ \Leftrightarrow & 15 x + 19 y = 784 \end{array}

Ainsi, $x\ $ et $\ y$ vérifient aussi l'équation suivante :

15 x + 19 y = 784 (2)

Alors, en résolvant le système d'équations formé des équations $(1)\ $ et $\ (2)$, on trouve les valeurs de $x\ $ et $\ y.$

Soit le système suivant :

{\begin{array}{rcrl} x + y & = & 48 & (1) \\ 15 x + 19 y & = & 784 & (2) \end{array}

Alors, en multipliant chaque membre de l'équation $(1)$ par $-15$, le système devient :

{\begin{array}{rcrl} - 15 x - 15 y & = & - 720 & (3) \\ 15 x + 19 y & = & 784 & (2) \end{array}

Puis, en additionnant membre à membre les équations $(2)\ $ et $\ (3)$, on trouve :

15 x + 19 y - 15 x - 15 y = 784 - 720

Ce qui donne alors : $4y=64$

D'où, $y=\dfrac{64}{4}=16$

Ensuite, en remplaçant cette valeur de $y$ dans l'équation $(1)$, on obtient :

x + 16 = 48

Ce qui entraine : $x=48-16=32$

Ainsi, $\boxed{x=32\ \text{ et }\ y=16}$

4) Calculons le pourcentage des candidats ayant une note comprise entre $[14\;;\ 16[.$

En effet, d'après le tableau, le nombre de candidats associé à cette classe est $x=32.$

Donc, le pourcentage des candidats ayant une note comprise entre $[14\;;\ 16[$ est donné par :

f = \frac{32}{160} \times 100 = 20

Par conséquent, $20\%$ des candidats ont une note comprise entre $[14\;;\ 16[.$

5) Dressons le tableau des $\text{E.C.C}\ $ et $\ \text{E.C.D}$ puis, construisons le diagramme des $\text{E.C.C}\ $ et $\ \text{E.C.D}$

En partant des effectifs donnés dans le tableau statistique, on obtient le tableau des $\text{E.C.C}\ $ et $\ \text{E.C.D}$ suivant :

\begin{array}{cccccc} Notes & [10; 12 [ & [12; 14 [ & [14; 16 [ & [16; 18 [ & [18; 20 [ \\ E.C.C & 48 & 88 & 120 & 144 & 160 \\ E.C.D & 160 & 112 & 72 & 40 & 16 \end{array}

Construisons le diagramme des $\text{E.C.C}\ $ et $\ \text{E.C.D}$

\begin{array}{rcl} Échelle : 1 c m & ⟶ & 2 points \\ 1 c m & ⟶ & 20 candidats \end{array}

6) Déterminons graphiquement la médiane.

Faisons apparaître les polygones des $\text{E.C.C}\ $ et $\ \text{E.C.D}$ sur le graphique.

Alors, le point de rencontre $M$ des ces deux polygones constitue le point médian.

Donc, son abscisse $m$ correspond exactement à la médiane de cette série.

Ainsi, en tenant compte de l'échelle, on trouve : $m=13.6$

D'où, la note médiane est égale à $13.6$

Par ailleurs, l'ordonnée de $M$ correspond à la moitié de l'effectif totale.

7) Déterminons la classe modale.

On rappelle que la classe modale d'une série statistique est la classe qui a le plus grand effectif.

Or, d'après le tableau statistique, on constate que la classe $[10\;;\ 12[$ a le plus grand effectif.

Par conséquent, elle représente la classe modale de cette série.

II. Le tableau suivant donne les angles de la répartition des catégories socioprofessionnelles des femmes en milliers.

Le nombre de femmes total des catégories est de $100\;\text{milliers}$

\begin{array}{cccccc} Catégories & Cadres & Cadres & Employés & Ouvriers & Personnel de \\ socioprofessionnelles & supérieurs & moyens & service \\ Angles & 90 & 54 & 72 & 108 & 36 \end{array}

1) Construisons le diagramme en secteur de la répartition des catégories socioprofessionnelles.

2) Calculons le nombre de femmes de chaque catégorie socioprofessionnelle.

En effet, l'angle d'occupation $\alpha^{\circ}$ correspondant à chaque catégorie socioprofessionnelle vérifie :

α^{\circ} = \frac{360^{\circ} \times n}{N}

où, $n$ est l'effectif partiel et $N$ l'effectif total représenté par le nombre total de femmes.

Donc, l'effectif partiel $n$ associé à chaque catégorie socioprofessionnelle est donné par :

n = \frac{α^{\circ} \times N}{360^{\circ}}

Alors, pour chaque catégorie socioprofessionnelle, en remplaçant $\alpha^{\circ}$ par son angle d'occupation et $N$ par $100\,000$, on trouve le nombre de femmes de cette catégorie socioprofessionnelle.

Ainsi :

pour $\alpha^{\circ}=90^{\circ}$, on a : $n=\dfrac{90\times 100\,000}{360}=25\,000$

pour $\alpha^{\circ}=54^{\circ}$, on a : $n=\dfrac{54\times 100\,000}{360}=15\,000$

pour $\alpha^{\circ}=72^{\circ}$, on a : $n=\dfrac{72\times 100\,000}{360}=20\,000$

pour $\alpha^{\circ}=108^{\circ}$, on a : $n=\dfrac{108\times 100\,000}{360}=30\,000$

pour $\alpha^{\circ}=36^{\circ}$, on a : $n=\dfrac{36\times 100\,000}{360}=10\,000$

Alors, en ajoutant dans le tableau statistique la ligne des effectifs, on obtient :

\begin{array}{cccccc} Catégories & Cadres & Cadres & Employés & Ouvriers & Personnel de \\ socioprofessionnelles & supérieurs & moyens & service \\ Angles & 90 & 54 & 72 & 108 & 36 \\ Nombre \\ de & 25 000 & 15 000 & 20 000 & 30 000 & 10 000 \\ femmes \end{array}

3) Dressons le tableau des fréquences cumulées croissantes.

Par ailleurs, pour calculer la fréquence $f$, en pourcentage, d'une catégorie socioprofessionnelle, on utilise la formule suivante :

f = \frac{n}{N} \times 100

où, $n$ est l'effectif partiel et $N$ l'effectif total

Donc,

pour $n=25\,000$, on a : $f=\dfrac{25\,000}{100\,000}\times 100=25$

pour $n=15\,000$, on a : $f=\dfrac{15\,000}{100\,000}\times 100=15$

pour $n=20\,000$, on a : $f=\dfrac{20\,000}{100\,000}\times 100=20$

pour $n=30\,000$, on a : $f=\dfrac{30\,000}{100\,000}\times 100=30$

pour $n=10\,000$, on a : $f=\dfrac{10\,000}{100\,000}\times 100=10$

On obtient alors le tableau suivant :

\begin{array}{cccccc} Catégories & Cadres & Cadres & Employés & Ouvriers & Personnel de \\ socioprofessionnelles & supérieurs & moyens & service \\ Fréquences en % & 25 & 15 & 20 & 30 & 10 \\ F.C.C & 25 & 40 & 60 & 90 & 100 \end{array}

4) Les modalités sont :

$-\ $ Cadres supérieurs

$-\ $ Cadres moyens

$-\ $ Employés

$-\ $ Ouvriers

$-\ $ Personnel de service

5) Le caractère observe est la catégorie socioprofessionnelle.

En effet, on sait que la catégorie socioprofessionnelle est une grandeur non mesurable.

Par conséquent, ce caractère est de nature qualitative.

6) On peut envisager la représentation graphique des fréquences cumulées croissantes et par la suite le polygone des $\text{F.C.C}$

Représentons alors le diagramme des $\text{F.C.C}$

$\text{Diagramme des fréquences cumulées croissantes}$

7) Déterminons la médiane.

En effet, on sait que la médiane correspond à $50\%$ des effectifs.

Donc, pour déterminer la médiane de cette série on place d'abord sur l'axe des ordonnées, la valeur $50.$

Puis, on projette cette valeur sur le polygone des $\text{F.C.C}$, parallèlement à l'axe des abscisses.

Ensuite, en suivant cette ligne de projection, on croise le diagramme en bâtons correspondant à la catégorie : Employés

Cette catégorie socioprofessionnelle représente alors la médiane.

III. La moyenne arithmétique d'une série statistique d'un caractère quantitatif continue est égale :

a) $\dfrac{1}{n}\sum\;n_{i}x_{i}$

Auteur:

Diny Faye

Commentaires

Anonyme (non vérifié)

jeu, 06/04/2020 - 20:13

Permalien

Il n'y a pas la correction de

Il n'y a pas la correction de l'exercice 8

répondre

Aïcha (non vérifié)

mer, 07/15/2020 - 14:45

Permalien

Exo23

Merci

répondre

Anonyme (non vérifié)

ven, 03/18/2022 - 08:45

Permalien

il n'y a pas la correction de

il n'y a pas la correction de l'exercice 12

répondre

Anonyme (non vérifié)

jeu, 07/23/2020 - 21:24

Permalien

Il n'y a pas la correction

Il n'y a pas la correction de l'exercice7

répondre

Martin Ndiaye (non vérifié)

mar, 08/04/2020 - 00:28

Permalien

Il n'y a pas la correction de

Il n'y a pas la correction de l'exercice 9

répondre

Anonyme (non vérifié)

ven, 08/28/2020 - 18:51

Permalien

correction de l'exo 6 svp

répondre

Anonyme (non vérifié)

mer, 09/02/2020 - 20:02

Permalien

Bonjour ! La correction de l

Bonjour ! La correction de l’exercice 23 s’il vous plaît

répondre

Awa sarr (non vérifié)

mar, 06/22/2021 - 21:22

Permalien

J'ai pas vue celle de 2002

répondre

Rokhaya (non vérifié)

mer, 06/23/2021 - 23:26

Permalien

il n'y a pas de correction de

il n'y a pas de correction de l exercice 15

répondre

Anonyme (non vérifié)

mar, 07/27/2021 - 00:20

Permalien

Il n'y a pas la correction de

Il n'y a pas la correction de l'exercice 12 bfem 2002

répondre

Anonyme (non vérifié)

jeu, 03/24/2022 - 23:34

Permalien

On peut avoir la correction

On peut avoir la correction de l’exercice 12 svp

répondre

Anonyme (non vérifié)

ven, 05/13/2022 - 00:44

Permalien

la correction de l exercice

la correction de l exercice 20

répondre

Anonyme (non vérifié)

ven, 06/10/2022 - 20:55

Permalien

Merci c'est excellent

répondre

Anonyme (non vérifié)

mer, 06/15/2022 - 22:13

Permalien

Il y'a pas la correction de l

Il y'a pas la correction de l'exercice 17

répondre

Anonyme (non vérifié)

dim, 07/17/2022 - 02:05

Permalien

Slt pourquoi je n'arrive pas

Slt pourquoi je n'arrive pas à trouver les corrections de tels exercices numéro 9,10,11....?

répondre

Coumbichou (non vérifié)

mer, 12/28/2022 - 17:54

Permalien

Exercice 18 19 21 22

répondre

Coumbichou (non vérifié)

mer, 12/28/2022 - 17:55

Permalien

Exercice 18 19 21 22

répondre

mayé faye (non vérifié)

ven, 01/27/2023 - 07:06

Permalien

merci bcp pour les exercice.

merci bcp pour les exercice. vraiment vous nous facilité la tache

répondre

Ababacar (non vérifié)

mar, 05/23/2023 - 00:21

Permalien

Erreur

Il y’a une erreur au niveau e l’exercice de synthèse 1 c’est 784 au lieu de 748

répondre

Irissa (non vérifié)

dim, 05/04/2025 - 21:54

Permalien

Ol ya des choses fosse dans l

Ol ya des choses fosse dans l'ecercice 1

répondre

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.

Vous êtes ici

Solution des exercices : Statistique 3e

Formulaire de recherche

Exercice 1 BFEM 1994

Exercice 2 BFEM BLANC 2005

Exercice 3 BFEM 2006

Exercice 4 BFEM 2007

Exercice 5 BFEM 2009

Exercice 6 BFEM 2008

Exercice 7

Exercice 8 BFEM 1997

Exercice 9

Exercice 10

Exercice 11 BFEM 1999

Exercice 12 BFEM 2002

Exercice 13

Exercice 14

Exercice 15

Exercice 16

Exercice 17

Exercice 18

Exercice 19

Exercice 20

Exercice 21

Exercice 22

Exercice 23

Exercice de synthèse

Commentaires

Ajouter un commentaire

Plain text