Plus on est âgé, moins les protéines sont assimilées et bien utilisées par le corps.

En ajoutant de la leucine à l'alimentation et aux protéines, le corps retrouve sa capacité d'assimilation et d'utilisation des protéines.

On peut trouver la leucine en quantité notable dans les arachides, le riz, le thon, le filet de boeuf…

Dans ce qui suit on se propose d’étudier la structure de la leucine et quelques-unes de ses propriétés.

1.1. La leucine est un acide a-aminé de formule semi-développée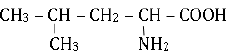

1.1.1. Donner le nom de la leucine dans la nomenclature officielle.

La molécule de leucine est-elle chirale ? Justifier la réponse.

1.1.2. La D-leucine présente des propriétés antalgiques utilisées en médecine dans le traitement de la douleur.

La $L$-leucine a une saveur sucrée et elle est utilisée comme additif alimentaire.

Ecrire les représentations de Fischer de la $L$-leucine et de la $D$-Leucine.

1.2. Dans une solution aqueuse de leucine il existe, entre autres espèces chimiques, un ion dipolaire appelé amphion ou zwittérion.

1.2.1 Ecrire la formule semi-développée de cet amphion.

1.2.2 L’amphion intervient dans deux couples acide/base.

Ecrire ces couples acide/base.

1.2.3 On considère la solution particulière de leucine dans laquelle la concentration de l’acide conjugué de l’amphion est égale à celle de la base conjuguée de l’amphion.

Le $pH$ de cette solution est appelé $pH$ isoélectrique, noté $pHi$.

1.2.3.1 Etablir l’expression de $pHi$ en fonction des $pka$ des deux couples acide/base associés à l’amphion que l’on notera $pk_{a1}$ et $pk_{a2}$. La valeur de $pHi$ dépend-elle de la concentration totale en acide aminé ?

1.2.3.2 Sachant que pour la leucine $pHi=6.0$ et que le $pka$ de l’un des couples est $9.6$, en déduire le $pka$ de l'autre couple acide/base.           
                          
1.3. On fait réagir la leucine avec un acide $a-aminé A$ de formule $R-CH(NH_{2})-COOH$ où $R$ est un radical alkyle.

On obtient un dipeptide de masse molaire $202\;g\cdot mol^{-1}$.

1.3.1. Déterminer la formule semi-développée de l’acide $a-aminé A$

1.3.2. On considère le dipeptide pour lequel la leucine est l’acide $a$-aminé $N$-terminal.

Ecrire la formule semi-développée de ce dipeptide.

Préciser les différentes étapes de la synthèse de ce dipeptide (il n’est pas demandé d’écrire les équations de réaction de ces étapes).

$M(C)=12\;g\cdot mol^{-1}\;;\ M(O)=16\;g\cdot mol^{-1}\;;\ M(H)=1\;g\cdot mol^{-1}\;;\ M(N)=14\;g\cdot mol^{-1}$.

L’eau oxygénée est un produit qui présente de nombreux avantages et s’utilise au quotidien, pour la maison mais aussi pour l’esthétique.

Le plus souvent ce produit est utilisé comme agent de blanchiment.

L’eau oxygénée a également des vertus stérilisantes et désinfectantes.

La décomposition de l’eau oxygénée est une réaction lente représentée par l’équation-bilan suivante :

$2 H_{2}O_{2}\rightarrow{2 H_{2}O + O_{2}}$

Pour étudier la cinétique de cette réaction, on introduit de l’eau oxygénée dans un ballon avec du chlorure de fer III (qui sert de catalyseur) de façon à obtenir une solution dont la concentration molaire initiale en eau oxygénée est de $6 mmol\cdot L^{-1}$.

La température est maintenue constante.

On effectue des prélèvements réguliers, qui sont ensuite dosés par une solution titrée de permanganate de potassium en milieu acide.

Les mesures réalisées ont permis de tracer la courbe représentant les variations de la concentration de l'eau oxygénée restante en fonction du temps.

2.1. Ecrire l'équation bilan de la réaction support du dosage sachant que les couples oxydants- réducteurs mis en jeux sont :

$MnO_{4^{-}}/Mn^{2^{+}}$ et $O_{2}/H_{2}O_{2}$.

2.2. Définir la vitesse volumique de disparition $v(t)$ de l’eau oxygénée à la date $t$.

Déterminer graphiquement sa valeur à l’instant $t=0$.

2.3 Déterminer le temps de demi-réaction et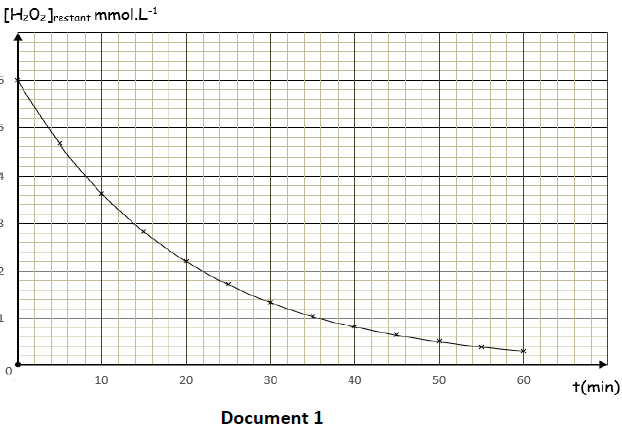 la valeur de la vitesse instantanée de disparition de l’eau oxygénée à cette date.

2.4 Comment évolue la vitesse instantanée de disparition de l’eau oxygénée au cours du temps ?

Justifier cette évolution.

2.5. On cherche à déterminer une relation simple entre la vitesse instantanée volumique de disparition de l’eau
oxygénée et sa concentration molaire dans le milieu réactionnel.

2.5.1. Dans les conditions de l'expérience la concentration
instantanée $Ct$ en eau oxygénée évolue conformément à la relation $Ct=Co e^{-K }t$ où $Co$ est la concentration d’eau oxygénée à la date $t=0$ et $K$ une constante.

Etablir la loi de variation $v(t)$ de la vitesse de disparition en fonction du temps $t$.

2.5.2. Tenant compte de la valeur trouvée à la question 2.2, calculer $K$.

En déduire une relation simple entre la vitesse de disparition $v(t)$ et la concentration $Ct$ de l’eau oxygénée à l’instant $t.$

En utilisant ce résultat, calculer la valeur de $v(t)$ à $t=14\;min$.

On considère un dispositif servant de lancement d’objets qui a la forme d’une portion de cercle de plan vertical, de longueur
$M_{0}M_{1}$, de centre $O$ et de rayon $r$ (document 2).

Son revêtement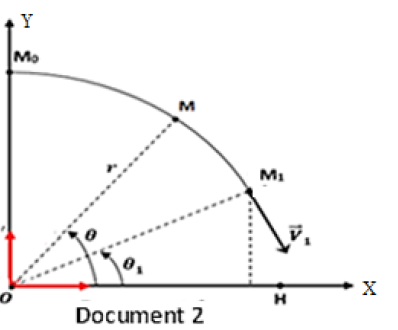 rend les frottements négligeables.

On étudie, dans le référentiel terrestre galiléen, le mouvement d’un ballon de masse $m$ supposé ponctuel posé sur le dispositif.

Dans toute la suite on rapporte le mouvement du ballon au
 repère cartésien orthonormé $(OX\;,\ OY)$; l’axe $OX$ étant
horizontal.

3.1. Le ballon est abandonné sur le dispositif à partir du point $M0$ qu’il quitte avec une vitesse initiale nulle pour aller en $M_{1}$.

Il glisse sans rouler le long de l’arc $M_{0}M_{1}$.

3.1.1. Faire le bilan des forces agissant sur le ballon lorsqu’il arrive en un point M de l’arc (voir document 2); reproduire le document et représenter ces forces en $M$.        
                                                         
3.1.2. Par application du théorème du centre d’inertie, trouver l’expression de l’intensité $R$ de la réaction au point $M$ en fonction du module $v$ de la vitesse, de l’angle $\theta$, de la masse $m$, du rayon $r$ et de l’intensité de la pesanteur $g$.

3.1.3. En appliquant le théorème de l’énergie cinétique, montrer que la vitesse du ballon en $M$ est telle que $v^{2}=2 g r(1-\sin\theta_{1})$. $(0.5\;pt)$

3.1.4 Le mobile quitte la piste au point $M_{1}$ d’élongation angulaire $\theta_{1}=(\vec{OX}\;,\ \vec{OM_{1}})$

Déterminer la valeur de l’angle $\theta_{1}$ .

En déduire l’expression de la vitesse $v_{1}$ du ballon au point $M_{1}$ en fonction de $g$ et $r$.
                                                                            
3.2. Dans la deuxième phase du mouvement, le mobile effectue une chute libre qui se termine par une réception au point $H$ sur un plan d’eau horizontal (voir document 2).

Dans cette phase, on choisit une nouvelle origine des dates $t=0$ au point $M_{1}$.

3.2.1. Exprimer les composantes du vecteur vitesse $\vec{v_{1}}$ en $M_{1}$ dans le repère $(OX\;,\ OY)$ en fonction de $\theta_{1}$ et $v_{1}$ .

3.2.2. Ecrire les équations horaires du mouvement durant cette phase et en déduire l’équation de la trajectoire du ballon.

3.2.3. Exprimer la distance $OH$ en fonction de $r$.

4.1 On applique une tension sinusoïdale de valeur efficace
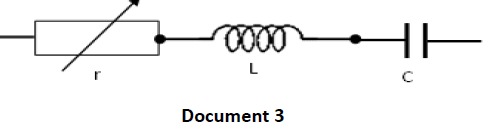
constante $U$ et de pulsation $\omega$ aux bornes d’un circuit comprenant en série un résistor de résistance variable $r$, une bobine d'inductance $L$, de résistance négligeable et un condensateur de capacité $C$.

Pour cette partie on prendra :

$U=0.2 V\;;\ L=2\cdot10^{-3} H\;;\ \omega=30.15\cdot10^{3} rad/s$.
' 
4.1.1. Exprimer le déphasage $\phi$ de la tension instantanée $u$ par rapport à l’intensité instantanée $i$ en fonction de $C\;,\ L\;,\ \omega$ et $r$. On posera :

$u(t)=Um\cos(\omega{t}+f)$ et $i(t)=Im\cos\omega{t}$.

4.1.2.En déduire les deux valeurs de $C$ qui produisent un déphasage tel que $IfI=\dfrac{\pi}{4}$ rad entre la tension et l'intensité pour $r=6\omega$.

4.1.3. Pour chacune des valeurs de la capacité $C$, calculer l’intensité efficace correspondante.

4.2. On s’intéresse maintenant aux variations de la puissance $P$ consommée dans la portion du circuit $(r L C)$ en fonction de la résistance $r$ pour une capacité $C=5\cdot10^{-7}F.$

4.2.1. Montrer que la puissance consommée dans cette portion de circuit peut être donnée par la relation :

$P=\dfrac{ar}{r^{2}+b}$ avec $a$ et $b$ des constantes à déterminer ; on prendra les valeurs de $U\;,\ L$ et $\omega$ indiquées en 4.1

4.2.2. En déduire la valeur optimale de $r$ pour une puissance maximale consommée.

4.2.3. En faisant varier la résistance $r$ du résistor, les mesures ont permis d’obtenir le tableau ci-dessous :
 

4.2.3.1. Représenter graphiquement $P$ en fonction de $r$.

Echelle : $1\;cm$ pour $2O$ et $1\;cm$ pour $0.50\cdot10^{-3} W$     
                                    
4.2.3.2. Par exploitation du graphe, trouver la valeur de $r$ notée $r_{0}$ pour laquelle la puissance consommée est maximale.

Comparer ce résultat à celui de la question 4.2.2.

4.2.4. Montrer que la puissance maximale consommée peut se mettre sous la forme $P^{m}=\dfrac{U2\cos^{2}f}{r_{0}}$ pour des valeurs quelconques mais constantes de $U\;,\ L\;,\ C\;,\ \omega$ (sauf pour celle qui annule la quantité $L\omega-\dfrac{1}{C\omega}$).

En déduire la valeur du déphasage $f$ entre la tension $u$ et l’intensité  $i$ .

Conclure.

4.2.5. A quel cas important correspond l’exception précédente ?

Dire qualitativement comment varie la puissance $P$ en fonction de r dans ce cas.

Le mercure, métal mythique du Moyen Âge, est le seul métal liquide à température ambiante.

Il est indissociable de l'or, qu'il permet de purifier.

Ce métal de symbole chimique $Hg$, est utilisable pour la fabrication de thermomètres, de lampes, en plombages et dans d’autres activités.

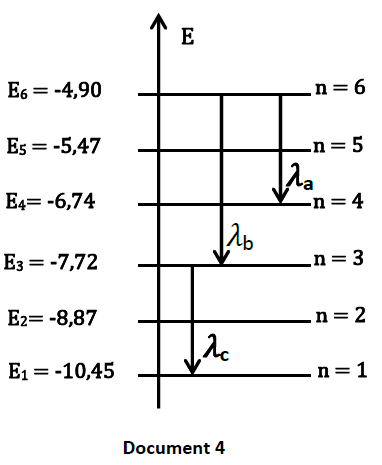
Le document ci-après représente quelques niveaux d’énergie de l’atome de mercure.

L’énergie d’un niveau $n$ est noté $E_{n }$; le niveau $n=1$ correspond à l'état fondamental.

5.1. A partir du document $4$, déterminer :

5.1.1. l’énergie des photons émis lors des transitions indiquées,

5.1.2. les valeurs des longueurs d'onde $\lambda{a}\;,\ \lambda{b}$ et $\lambda{c}$.

On précisera le domaine spectral auquel appartient chaque longueur d'onde (se référer au document $5$).

On donne :

$h=6.62\cdot10^{-34}J\cdots^{-1}\;;\ 1eV=1.6.10^{-19}J$

vitesse de la lumière dans le vide :

$C=3.108\;m\cdot s^{-1}$

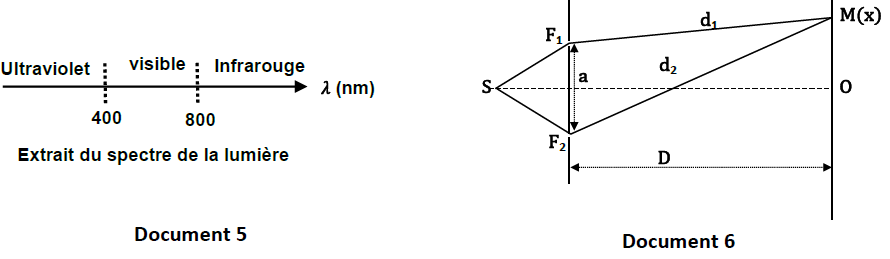
5.2. Une source $S$ émet une radiation lumineuse de longueur d’onde $\lambda_{1}$ et éclaire deux fentes fines de Young $F_{1}$ et $F_{2}$ distantes de $a.$ La source $S$ est à égale distance de ces deux fentes.

On place un écran $(E)$, parallèle au plan des fentes et situé à une distance $D$ de celui-ci (document $6$).

On donne : $a=2\;mm\;;\ D=486\;mm$.

5.2.1. Donner les conditions d’obtention du phénomène d’interférences.

5.2.2. Le point $O$ de l'écran, origine de l'axe parallèle à  $F_{1}F_{2}$, est sur la droite bissectrice de $F_{1}F_{2}$. $M$ est un point de l'écran $(E)$ d'abscisse $x$.

5.2.2.1. Etablir l’expression de la différence de marche $F_{1}F_{2}$ entre deux rayons lumineux issus de $F_{1}$ et $F_{2}$ arrivant
en un point $M(x)$ en fonction de $a\;,\ D$ et $x$.

5.2.2.2. En déduire l’expression donnant les abscisses des points de l’écran situés sur une frange obscure.

5.2.2.3. La distance séparant la $5^{ème}$ frange brillante et la $3^{ème}$ frange sombre de part et d’autre de la frange centrale compté zéro est $d=1.024\;mm$.

En déduire la valeur de $\lambda_{1}$.

5.3. La source $S$ émet simultanément la radiation de longueur d’onde $\lambda_{1}$ calculée précédemment et une autre radiation de longueur d’onde $\lambda_{2}$ telle que $\dfrac{\lambda_{2}}{\lambda_{1}}=1.5$.

5.3.1. Au point $O$ de l’écran, on a une superposition des franges brillantes correspondant aux deux radiations. $A$ quelle distance $l_{1}$ du centre $O$ de l’écran a-t-on pour la première fois une superposition entre les franges brillantes ?

5.3.2. Peut-on observer une extinction totale sur l’écran? Justifier la réponse.