Vous êtes ici

Solution des exercices : Équilibre d'un solide mobile autour d'un axe - 2nd S

Classe:

Seconde

Exercice 1

Un chemin forestier est fermé par une barrière constituée d'une poutre (1) et d'un contre-poids (2).

La barrière peut tourner autour d'un axe

$\Delta$ perpendiculaire en

$O$ au plan de la figure

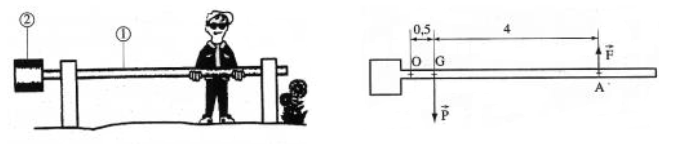
Les cotes sont en mètres. La masse de la barrière est

$60\;kg\;;\ G$ est son centre de gravité.

Un promeneur veut la soulever en exerçant en

$A$ une force

$\vec{F}$ d'intensité

$100\;N.$

1) a) Calculons l'intensité du poids

$\vec{P}$ de la barrière.

Soit :

$P=m.g\$ avec,

$g=10\;N.kg^{-1}.$

A.N :

$P=60\times 10=600$

Donc,

$\boxed{P=600\;N}$

b) Calculons le moment de

$\vec{P}$ par rapport à

$\Delta.$

On a :

$\mathcal{M}_{\Delta}(\vec{P})=P\cdot OG$

A.N :

$\mathcal{M}_{\Delta}(\vec{P})=600\times 0.5=300$

Ainsi,

$\boxed{\mathcal{M}_{\Delta}(\vec{P})=300\;Nm}$

c) Calculons le moment de

$\vec{F}$ par rapport à

$\Delta.$

L'expression du moment de

$\vec{F}$ par rapport à

$\Delta$ est donnée par :

$\mathcal{M}_{\Delta}(\vec{F})=P\cdot OA$

A.N :

$\mathcal{M}_{\Delta}(\vec{F})=100\cdot 4=400$

D'où,

$\boxed{\mathcal{M}_{\Delta}(\vec{F})=400\;Nm}$

2) Le promeneur peut soulever la barrière car

$\mathcal{M}_{\Delta}(\vec{F})>\mathcal{M}_{\Delta}(\vec{P})$

Exercice 2

Le chargeur représenté ci-dessous se compose :

$-\$ d'un châssis et du conducteur de masse

$400\;kg$ ;

$-\$ de son chargement de masse

$420\;kg$ ;

$-\$ d'un système de levage et du godet de masse

$150\;kg.$

Le poids du châssis s'applique au point

$G_{1}$

Le poids du chargement au poing

$G_{2}$

Le poids du système de levage au poing

$G_{3}$

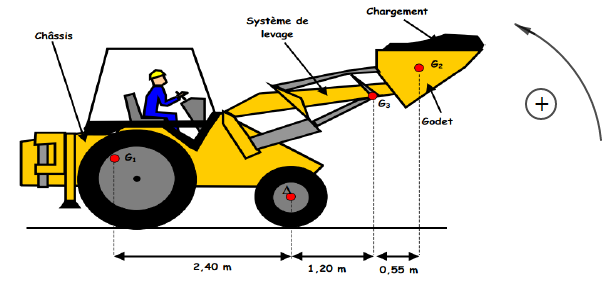
1) Calculons les intensités des poids

$P_{1}\;,\ P_{2}\$ et

$\ P_{3}$ du châssis, du chargement et du système de levage

Soit alors :

$P_{1}=m_{1}.g=400\times 10=40\cdot 10^{2}$

Donc,

$\boxed{P_{1}=40\cdot 10^{2}\;N}$

$P_{2}=m_{2}.g=420\times 10=42\cdot 10^{2}$

Ainsi,

$\boxed{P_{2}=42\cdot 10^{2}\;N}$

$P_{3}=m_{3}.g=150\times 10=15\cdot 10^{2}$

Par suite,

$\boxed{P_{3}=15\cdot 10^{2}\;N}$

2) Calcul du moment du poids

$P_{1}$ par rapport à l'axe

$\Delta$ de la roue avant.

Choisissons un sens positif de rotation (voir figure)

Soit :

$\mathcal{M}_{\Delta}(\vec{P}_{1})=P_{1}\cdot d_{1}$

A.N :

$\mathcal{M}_{\Delta}(\vec{P}_{1})=40\cdot 10^{2}\cdot 2.40=96\cdot 10^{2}$

D'où,

$\boxed{\mathcal{M}_{\Delta}(\vec{P}_{1})=96\cdot 10^{2}\;Nm}$

3) Calculons le moment du poids

$P_{2}$ par rapport à l'axe

$\Delta$ de la roue avant.

On a :

$\mathcal{M}_{\Delta}(\vec{P}_{2})=-P_{2}\cdot d_{2}$

Donc,

$\mathcal{M}_{\Delta}(\vec{P}_{2})=-42\cdot 10^{2}\cdot 1.75=-73.5\cdot 10^{2}$

Par suite,

$\boxed{\mathcal{M}_{\Delta}(\vec{P}_{2})=-73.5\cdot 10^{2}\;Nm}$

4) Calcul du moment du poids

$P_{3}$ par rapport à l'axe

$\Delta$ de la roue avant.

Soit :

$\mathcal{M}_{\Delta}(\vec{P}_{3})=-P_{3}\cdot d_{3}$

A.N :

$\mathcal{M}_{\Delta}(\vec{P}_{3})=-15\cdot 10^{2}\cdot 1.20=-18\cdot 10^{2}$

D'où,

$\boxed{\mathcal{M}_{\Delta}(\vec{P}_{3})=-18\cdot 10^{2}\;Nm}$

5) Vérifions si le chargeur ainsi chargé pivote autour de l'axe

$\Delta$

On a :

$\begin{array}{rcl}\left|\mathcal{M}_{\Delta}(\vec{P}_{2})+\mathcal{M}_{\Delta}(\vec{P}_{3})\right|&=&\left|-73.5\cdot 10^{2}-18\cdot 10^{2}\right|\\ \\&=&91.5\end{array}$

Donc,

$\left|\mathcal{M}_{\Delta}(\vec{P}_{2})+\mathcal{M}_{\Delta}(\vec{P}_{3})\right|=91.5\;Nm$

Comme

$\mathcal{M}_{\Delta}(\vec{P}_{})=96\cdot 10^{2}\;Nm$ alors,

$\mathcal{M}_{\Delta}(\vec{P}_{})>\left|\mathcal{M}_{\Delta}(\vec{P}_{2})+\mathcal{M}_{\Delta}(\vec{P}_{3})\right|$

Par conséquent, le chargeur ainsi chargé pivote autour de l'axe

$\Delta.$

6) Déterminons la charge maximale que peut transporter le godet

Soit :

$\mathcal{M}_{\Delta}(\vec{P}_{1})+\mathcal{M}_{\Delta}(\vec{P}_{2})+\mathcal{M}_{\Delta}(\vec{P}_{3})=0$ alors,

$\begin{array}{rcl}\mathcal{M}_{\Delta}(\vec{P}_{2})=-\mathcal{M}_{\Delta}(\vec{P}_{1})-\mathcal{M}_{\Delta}(\vec{P}_{3})&\Rightarrow&-P_{2}.d_{2}=-\mathcal{M}_{\Delta}(\vec{P}_{1})-\mathcal{M}_{\Delta}(\vec{P}_{3})\\ \\&\Rightarrow&P_{2}=\dfrac{\mathcal{M}_{\Delta}(\vec{P}_{1})+\mathcal{M}_{\Delta}(\vec{P}_{3})}{d_{2}}\\ \\&\Rightarrow&M_{2}.g=\dfrac{\mathcal{M}_{\Delta}(\vec{P}_{1})+\mathcal{M}_{\Delta}(\vec{P}_{3})}{d_{2}}\\ \\&\Rightarrow&M_{2}=\dfrac{\mathcal{M}_{\Delta}(\vec{P}_{1})+\mathcal{M}_{\Delta}(\vec{P}_{3})}{d_{2}.g}\end{array}$

Donc,

$M_{2}=\dfrac{\mathcal{M}_{\Delta}(\vec{P}_{1})+\mathcal{M}_{\Delta}(\vec{P}_{3})}{d_{2}.g}$

A.N :

$M_{2}=\dfrac{96\cdot 10^{2}-18\cdot 10^{2}}{1.75\times 10}=446$

D'où,

$\boxed{M_{2}=446\;kg}$

Exercice 3

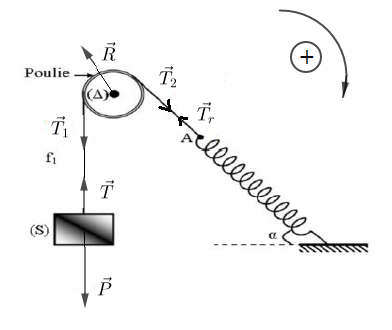
Un solide

$(S)$ de masse

$m=200\;g$ est relié à un fil de masse négligeable passant par la gorge d'une poulie à axe fixe

$(\Delta)$ , de masse négligeable et de rayon

$r.$

L'autre extrémité du fil est attachée à un ressort de raideur

$k$ et de masse négligeable.

A l'équilibre, l'axe du ressort fait un angle

$\alpha=30^{\circ}$ avec l'horizontale et le ressort est allongé de

$\Delta l=4\;cm.$ On néglige tout type de frottement.

1) a) Représentons les forces exercées sur le solide

$(S).$

b) Écrivons la condition d'équilibre de

$(S)$

$\vec{P}+\vec{T}=\vec{0}$

Déterminons l'expression de la tension du fil

$f_{1}.$

On a :

$\begin{array}{rcl}\vec{P}+\vec{T}=\vec{0}&\Rightarrow&m.g-T=0\\ \\&\Rightarrow&T=m.g\end{array}$

Calcul de sa valeur.

$T=m.g=200.10^{-3}\times 10=2$

Donc,

$\boxed{T=2\;N}$

2) a) Représentons les forces exercées sur la poulie.

Voir figure

b) Détermination de la tension du fil

$f_{2}$

Le théorème des moments s'écrit :

$\begin{array}{rcl} M_{\Delta}(\vec{T_{1}})+M_{\Delta}(\vec{T_{2}})+M_{\Delta}(\vec{R})=0&\Rightarrow&-T_{1}r+T_{2}r+0=0\\ \\&\Rightarrow&T_{2}r=T_{1}r\\ \\&\Rightarrow&T_{2}=T_{1}\end{array}$

Le fil transmet les forces donc :

$\begin{array}{rcl} T_{1}=T&\Rightarrow&T_{2}=T\\ \\&\Rightarrow& T_{2}=2\;N\end{array}$

c) Déduction de la tension du fil

$f_{2}$ au point

$A.$

Le fil transmet les forces alors :

$T_{r}=T_{2}\ \Rightarrow\ T_{r}=2\;N$

3) Déterminons la valeur de la raideur du ressort

$k.$

On a :

$T_{r}=k\Delta l\ \Rightarrow\ k=\dfrac{T_{r}}{\Delta l}$

A.N :

$k=\dfrac{2.0}{4.10^{-2}}=25$

Ainsi,

$\boxed{k=25\;N.m^{-1}}$

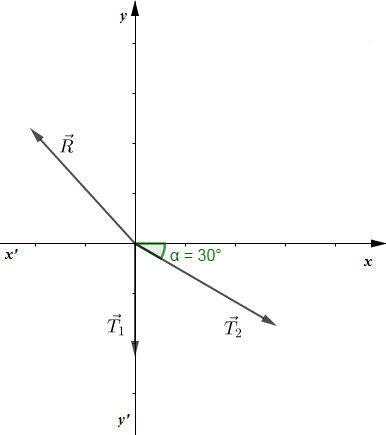
4) Par projection de la relation vectorielle, traduisant l'équilibre de la poulie, dans un repère orthonormé, montrons que la valeur de la réaction R de l'axe

$(\Delta)$ est

$R=mg\sqrt{2(1+\sin \alpha)}$

La condition d'équilibre s'écrit :

$\vec{T_{1}}+\vec{T_{2}}+\vec{R}=\vec{0}$

En projetant la relation vectorielle suivant les axes

$x’x\$ et

$\ y’y$ , il vient :

$0+T_{2}\cos \alpha-R_{x}=0\ \Rightarrow\ R_{x}=T_{2}\cos \alpha=mg\cos \alpha$

$\begin{array}{rcl} T_{1}+T_{2}\sin \alpha-R_{y}=0&\Rightarrow&R_{y}=T_{1}+T_{2}\sin \alpha\quad\text{or, }\ T_{1}=T_{2}=mg\\ \\&\Rightarrow&R_{y}=mg(1+\sin \alpha)\end{array}$

Soit alors :

$\begin{array}{rcl} R&=&\sqrt{R_{x}^{2}+R_{y}^{2}}\\ \\&=&\sqrt{(m.g\cos \alpha)^{2}+(m.g(1+\sin \alpha))^{2}}\\ \\&=&m.g\sqrt{(\cos \alpha)^{2}+(1+\sin \alpha)^{2}}\\ \\&=&m.g\sqrt{\cos^{2}\alpha+1+2\sin \alpha+\sin^{2}\alpha}\\ \\&=&m.g\sqrt{2+2\sin \alpha}\\ \\&=&m.g\sqrt{2(1+\sin \alpha)}\end{array}$

Calcul de sa valeur

$\begin{array}{rcl} R&=&m.g\sqrt{2(1+\sin \alpha)}\\ \\&=&200.10^{-3}\times 10\sqrt{2(1+\sin 30^{\circ})}\\ \\&=&0.34\end{array}$

D'où,

$\boxed{R=0.34\;N}$

Exercice 4

On dispose d'une règle homogène, de masse négligeable, pouvant tourner autour d'un axe horizontal

$\Delta$ passant par son centre d'inertie

$O.$ On veut connaître le comportement de la règle dans les situations suivantes :

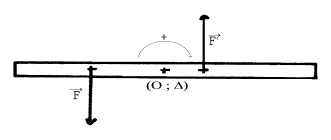
1) La règle, initialement au repos, est soumise à un seul couple de forces

$(\vec{F}\;,\ \vec{F'})\ :$ , indiquons quel est le comportement de la règle et donnons le signe du moment du couple de forces.

Le couple de forces fait tourner la règle dans un sens opposé à celui du sens positif choisi. Le signe du moment du couple est donc négatif.

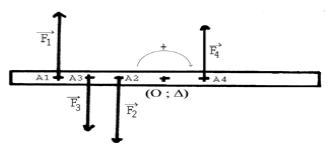
2.1) Calcul du moment de chaque couple.

Soit :

$F_{1}=F_{2}=2.5\times 2\ \Rightarrow\ F_{1}=F_{2}=5\;N$

$d=1.6\times 10\ \Rightarrow\ d=16\;cm$

$F_{3}=F_{4}=2\times 2\ \Rightarrow\ F_{3}=F_{4}=4\;N$

$d'=3.0\times 10\ \Rightarrow\ d'=30\;cm$

Alors,

$M_{\Delta}(F_{1}\;,\ F_{2})=F_{1}.d=5\times 16.10^{-2}$

Donc,

$\boxed{M_{\Delta}(F_{1}\;,\ F_{2})=0.80\;Nm}$

$M_{\Delta}(F_{1}\;,\ F_{2})=F_{1}.d=5\times 16.10^{-2}$

Ainsi,

$\boxed{M_{\Delta}(F_{1}\;,\ F_{2})=0.80\;Nm}$

$M_{\Delta}(F_{3}\;,\ F_{4})=-F_{3}.d'=4\times 30.10^{-2}$

D'où,

$\boxed{M_{\Delta}(F_{3}\;,\ F_{4})=-1.20\;Nm}$

2.2) Exprimons la condition d'équilibre de la règle.

$M_{\Delta}(F_{1}\;,\ F_{2})+M_{\Delta}(F_{3}\;,\ F_{4})=0$

Montrons alors que la règle n'est pas en équilibre mais en rotation non uniforme.

On a :

$\left|M_{\Delta}(F_{3}\;,\ F_{4})\right|>M_{\Delta}(F_{1}\;,\ F_{2})$

Donc, la règle n'est pas équilibre mais en rotation non uniforme.

Cette rotation se fait dans le sens négatif.

2.3) On veut obtenir l'équilibre de cette règle :

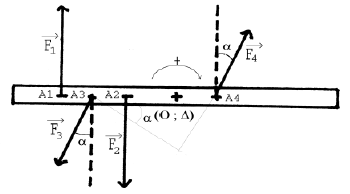
2.3.1) Pour cela, on déplace le point d'application

$A_{3}$ de la force

$\vec{F}_{3}$ , déterminons la position de

$A_{3}$ par rapport à

$O$ pour que la règle soit en équilibre.

On sait que :

$M_{\Delta}(F_{1}\;,\ F_{2})+M_{\Delta}(F_{3}\;,\ F_{4})=0$

Donc,

$\begin{array}{rcl} M_{\Delta}(F_{3}\;,\ F_{4})=-M_{\Delta}(F_{1}\;,\ F_{2})&\Rightarrow&-F_{3}.d=-M_{\Delta}(F_{1}\;,\ F_{2})\\ \\&\Rightarrow&d=\dfrac{M_{\Delta}(F_{1}\;,\ F_{2})}{F_{3}}\\ \\&\Rightarrow&d=\dfrac{0.80}{4}\\ \\&\Rightarrow&d=0.20\;m\end{array}$

2.3.2) Donnons l'expression du moment du couple

$(\vec{F_{3}}\;,\ \vec{F_{4}})$ en fonction de

$\alpha\;,\ F_{3}\;,\ A_{3}A_{4}$

On a :

$M_{\Delta}(F_{3}\;,\ F_{4})=-F_{3}.A_{3}A_{4}.\cos\alpha$

Détermination de la valeur de

$\alpha$ pour laquelle la règle est en équilibre.

On a :

$M_{\Delta}(F_{1}\;,\ F_{2})+M_{\Delta}(F_{3}\;,\ F_{4})=0\ \Rightarrow\ M_{\Delta}(F_{3}\;,\ F_{4})=-M_{\Delta}(F_{1}\;,\ F_{2})$

Alors,

$\begin{array}{rcl} -F_{3}.A_{3}A_{4}.\cos\alpha=-M_{\Delta}(F_{1}\;,\ F_{2})&\Rightarrow&\cos\alpha=\dfrac{M_{\Delta}(F_{1}\;,\ F_{2})}{F_{3}.A_{3}A_{4}}\\ \\&\Rightarrow&\alpha=\cos^{-1}\left(\dfrac{(M_{\Delta}(F_{1}\;,\ F_{2})}{F_{3}.A_{3}A_{4}}\right)\\ \\&\Rightarrow&\alpha=\cos^{-1}\left(\dfrac{0.80}{4\times 0.30}\right)\\ \\&\Rightarrow&\alpha=48.2^{\circ}\end{array}$

Donc,

$\boxed{\alpha=48.2^{\circ}}$

Commentaires

Babacar ndongo (non vérifié)

ven, 04/25/2025 - 01:29

Permalien

Baba

Pourquoi l'exercice numéro 5, on n'a pas donné la longueur de AB

répondre

J’aime les maths (non vérifié)

mer, 05/14/2025 - 20:55

Permalien

Les exercices sont biens mais

Les exercices sont biens mais on ne peut pas les faire si on a pas la correction sinon ça ne sert à rien merci pour l’Effort mais svp donner nous toutes la correction

répondre

Lamine (non vérifié)

lun, 06/02/2025 - 23:11

Permalien

Demande d' exercice non corrigée

Je veux vous m' aider les correction sur les autres exercices

répondre

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.

Solution des exercices : Équilibre d'un solide mobile autour d'un axe - 2nd S

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Commentaires

Baba

Les exercices sont biens mais

Demande d' exercice non corrigée

Pages

Ajouter un commentaire

Plain text

Vous êtes ici

Solution des exercices : Équilibre d'un solide mobile autour d'un axe - 2nd S

Formulaire de recherche

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Commentaires

Baba

Les exercices sont biens mais

Demande d' exercice non corrigée

Pages

Ajouter un commentaire

Plain text