Solution des exercices : Limites et continuité-Ts
Classe:
Terminale
Déterminer l'ensemble de définition d'une fonction
Exercice 1
1) Le réel $x$ appartient à l'ensemble de définition $D_{f}$ de la fonction $f$ si, et seulement si, il est solution du système : $$(\ast)\ \left\lbrace\begin{array}{lcl} x^{2}+2x+3&\geq& 0\quad(1)\\ x^{2}-3x-4&\geq& 0\quad(2) \end{array}\right.$$
Le discriminant : $\Delta$ associé au trinôme : $x^{2}+2x+3$ vaut :
$$\Delta=2^{2}-4\times 1\times 3=4-12=-8.$$
Il est strictement négatif et le coefficient de « $x^{2}$ » est positif (il vaut $1).$
On en déduit :
$$\forall\,x\in\mathbb{R}\;,\ x^{2}+2x+3>0$$
Le discriminant $\Delta$ associé au trinôme : $x^{2}-3x-4$ vaut :
$$\Delta=(-3)^{2}-4\times 1\times(-4)=9+16=25.$$
Il est strictement positif et on vérifie aisément que le trinôme a pour racines $-1$ et $4.$
On en déduit que $(x^{2}-3x-4\geq 0)\Leftrightarrow(x\leq-1)\text{ ou }(x\geq 4).$
Faisons un tableau conjoint pour déterminer l'ensemble des solutions du système $(\ast)$
$$\begin{array}{|c|lcccccr|} \hline x&-\infty& &-1& &4& &+\infty\\ \hline \text{L'inéquation (1) est vérifiée}& &\text{oui}&|&\text{oui}&|&\text{oui}&\\ \hline \text{L'inéquation (2) est vérifiée}& &\text{oui}&|&\text{non}&|&\text{oui}&\\ \hline \text{Le système est vérifiée}& &\text{oui}&|&\text{non}&|&\text{oui}&\\ \hline \end{array}$$
Finalement : $D_{f}=]-\infty\;;\ -1]\cup[4\;;\ +\infty[.$
2) Soit $f_{1}$ la fonction définie par : $f_{1}(x)=x+\dfrac{2}{\sqrt{x+4}}.$
Alors $f_{1}(x)$ existe si et seulement si $x+4>0$, soit : $x>-4.$
$D_{f1}=]-4\;;\ +\infty[\text{ et }D_{f1}\cap]-\infty\;;\ 0]=]-4\;;\ 0].$
Soit $f_{2}$ la fonction définie par : $f_{2}(x)=x+3-\sqrt{x^{2}+x-2}.$
Alors $f_{2}(x)$ existe si et seulement si $x^{2}+x-2\geq 0\Leftrightarrow(x\leq-2)$ ou $(x\geq 1).$
$D_{f2}=]-\infty\;;\ -2]\cup[1\;;\ +\infty[\text{ et }D_{f2}\cap[0\;;\ +\infty[=[1\;;\ +\infty[.$
3) $f(x)$ existe si et seulement si : $\left\lbrace\begin{array}{lcl} x^{2}+5x&\neq&0\quad(1)\text{ et}\\ \dfrac{1-3x}{x^{2}+5x}&\geq&0\quad(2) \end{array}\right.$
La condition $(1)$ équivaut à $x\neq 0$ et $x\neq -5.$
La condition $(2)$ se résout à l'aide d'un tableau de signes :
$$\begin{array}{|c|lcccccccr|} \hline x&-\infty& &-5& &-\dfrac{1}{3}& &0& &+\infty\\ \hline 1-3x& &+&|&+&|&+&|&-&\\ \hline x^{2}+5x& &+&|&-&|&+&|&+&\\ \hline Q& &+&||&-&||&+&|&-&\\ \hline \end{array}$$
Il en résulte que : $D_{f}=]-\infty\;;\ -5[\cup\left]0\;;\ \dfrac{1}{3}\right].$
4) $f(x)$ existe si et seulement si : $\left\lbrace\begin{array}{lcl} 1-3x&\geq&0\quad(1)\text{ et}\\ x^{2}+5x&>&0\quad(2) \end{array}\right.$
On résout ces deux inéquations simultanées à l'aide d'un tableau de signes :
$$\begin{array}{|c|lcccccccr|} \hline x&-\infty& &-5& &0& &\dfrac{1}{3}& &+\infty\\ \hline 1-3x& &+&|&+&|&+&|&-&\\ \hline x^{2}+5x& &+&||&-&||&+&|&+&\\ \hline \end{array}$$
Il en résulte que : $D_{f}=]-\infty\;;\ -5[\cup\left]0\;;\ \dfrac{1}{3}\right].$
5) $f(x)$ existe si et seulement si : $x^{3}-12x+16>0.$
On peut remarquer que $2$ est une racine évidente du polynôme au premier membre de cette inégalité.
Par la méthode de Hörner, par exemple, on vérifie que celui-ci se factorise en $(x+4)(x-2)^{2}.$
Il est alors clair que $D_{f}=]-4\;;\ 2[\cup]2\;;\ +\infty[.$
6) $f(x)$ existe si et seulement si : Il en résulte que : $\left\lbrace\begin{array}{lcl} 1-x&>&0\quad(1)\text{ et}\\ |x-3|-5&\neq&0\quad(2) \end{array}\right.$
La condition $(1)$ équivaut à : $x<1$ et le contraire de la condition $(2)$ s'écrit : $|x-3|=5$, ce qui équivaut à $\left\lbrace\begin{array}{lcl} x-3&=&5\\ x-3&=&-5 \end{array}\right.\text{ou}$ soit $x=8$ ou $x=-2.$
La condition $(2)$ signifie donc qu'on doit avoir :
$x\neq 8$ et $x\neq -2.$
Or, si $x<1$, $x$ est certainement différent de $8.$
En résumé, $x$ doit être inférieur (strictement) à $1$ et différent de $-2$, ce qui donne : $D_{f}=]-\infty\;;\ -2[\cup]-2\;;\ 1[.$
7) $f(x)$ existe si et seulement si : $\left\lbrace\begin{array}{lcl} x&\geq 0\quad(1)\text{ et}\\ \pi x&\text{n'est pas un multiple entier de}&\pi\quad(2) \end{array}\right.$
En résumé, si $x$ n'est pas un entier naturel.
$D_{f}=\mathbb{R}\setminus\mathbb{N}.$
8) $f(x)$ existe si et seulement si : $x$ n'est pas un multiple impair de $\dfrac{\pi}{2}$ (pour que $\tan x$ existe) et $x^{2}-\pi^{2}$ n'est pas un multiple entier de $\pi.$
Or $x^{2}-\pi^{2}=k\pi\Leftrightarrow x^{2}=\pi(k+\pi)\Leftrightarrow$
$$\left\lbrace\begin{array}{lcl} k&\geq &-\pi\\ x=\sqrt{\pi(k+\pi)}&\text{ou}&x=-\sqrt{\pi(k+\pi)} \end{array}\right.$$
$D_{f}$ est donc l'ensemble $\mathbb{R}$ privé des nombres de la forme $(2h+1)\dfrac{\pi}{2}$, où $h$ est un entier relatif quelconque, et de la forme $\sqrt{\pi(k+\pi)}\text{ ou }-\sqrt{\pi(k+\pi)}$, où $k$ est un entier relatif supérieur ou égal à $-3.$
9) $f(x)$ existe si et seulement si : $\left\lbrace\begin{array}{lcl} 2\sin x-1&\geq&0\quad(1)\text{ et}\\ 2\sin^{2}x-1&\neq& 0\quad(2) \end{array}\right.$
Résolvons ces conditions dans $[0\;;\ 2\pi[$ par exemple.
Pour cela, on s'aide d'un schéma du cercle trigonométrique (voir le rappel sur les inéquations trigonométriques ci-dessus) :
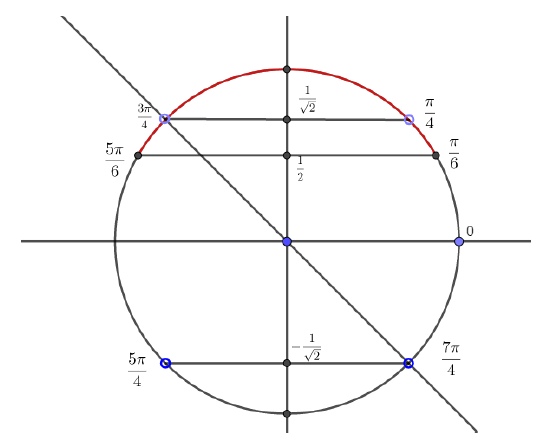
1) signifie qu'un point d'abscisse curviligne $x$ doit être situé sur l'arc rouge et $(2)$ signifie que $x$ doit être différent de $\dfrac{\pi}{4}$, $\dfrac{3\pi}{4}$, $\dfrac{5\pi}{4}$ et $\dfrac{7\pi}{4}.$
Finalement $D_{f}\cap[0\;;\ 2\pi[=\left[\dfrac{\pi}{6}\;;\ \dfrac{\pi}{4}\right[\cup\left]\dfrac{\pi}{4}\;;\ \dfrac{3\pi}{4}\right[\cup\left]\dfrac{3\pi}{4}\;;\ \dfrac{5\pi}{6}\right].$
On en déduit le domaine de définition complet dans $\mathbb{R}$ en ajoutant $2\pi$ à chaque extrémité d'intervalle :
$D_{f}$ est la réunion des ensembles de la forme :
$\left[\dfrac{\pi}{6}+2k\pi\;;\ \dfrac{\pi}{4}+2k\pi\right[\cup\left]\dfrac{\pi}{4}+2k\pi\;;\ \dfrac{3\pi}{4}+2k\pi\right[\cup\left]\dfrac{3\pi}{4}+2k\pi\;;\ \dfrac{5\pi}{6}+2k\pi\right]$, pour $k$ appartenant à $\mathbb{Z}.$
Calculs de limites
Exercice 2
1) La fonction $f\ :\ x\mapsto x^{3}-3x+5$ est une fonction polynôme.
Par conséquent $\lim_{\,x\rightarrow 1}(x^{3}-3x+5)=f(1)=1^{3}-3\times 1+5=3.$
2) La fonction $f\ :\ x\mapsto 2x^{2}+x-2$ est une fonction polynôme.
Par conséquent $\lim_{\,x\rightarrow -1}(2x^{2}+x-2)=f(-1)=2\times(-1)^{2}-1-2=-1.$
3) La fonction $f\ :\ x\mapsto\dfrac{3x+1}{x-3}$ est une fonction rationnelle définie au point $x_{0}=2.$
Par conséquent $\lim_{\,x\rightarrow 2}\left(\dfrac{3x+1}{x-3}\right)=f(2)=\dfrac{3\times 2+1}{2-3}=-7.$
Extension de la notion de limite
Exercice 3
1) a) $\ast\ \lim_{\,x\rightarrow +\infty}(x^{2}-3x+1)=\lim_{x\rightarrow +\infty}(x^{2})=+\infty$ (application du théorème sur la limite d'un polynôme à l'infini et d'une limite de référence).
$\ast\ \lim_{\,x\rightarrow -\infty}(x^{2}-3x+1)=\lim_{x\rightarrow -\infty}(x^{2})=+\infty$ (application du théorème sur la limite d'un polynôme à l'infini et d'une limite de référence).
b) La fonction $f\ :\ \mapsto(x^{3}-x)(x+1)$ est visiblement une fonction polynôme dont le monôme de plus haut degré est $x^{3}\times x=x^{4}.$
On obtient alors :
$\ast\ \lim_{\,x\rightarrow +\infty}[(x^{3}-x)(x+1)]=\lim_{\,x\rightarrow +\infty}(x^{4})=+\infty.$
$\ast\ \lim_{\,x\rightarrow -\infty}[(x^{3}-x)(x+1)]=\lim_{\,x\rightarrow -\infty}(x^{4})=+\infty.$
c) En tenant compte du signe de l'expression sous la valeur absolue, on voit que $f(x)$ s'exprime de deux manières suivant les valeurs de $x$ : $\left\lbrace\begin{array}{lllllll} \text{Si }x&\leq&3\;,&\text{alors}&f(x)&=&x^{2}-x+3\\ \text{Si }x&\geq&3\;,&\text{alors}&f(x)&=&x^{2}+x-3 \end{array}\right.$
Il en résulte que :
$\lim_{\,x\rightarrow +\infty}f(x)=\lim_{\,x\rightarrow +\infty}(x^{2}+x-3)=\lim_{\,x\rightarrow +\infty}(x^{2})=+\infty.$
Et : $\lim_{\,x\rightarrow -\infty}f(x)=\lim_{\,x\rightarrow -\infty}(x^{2}-x+3)=\lim_{\,x\rightarrow -\infty}(x^{2})=+\infty.$
d) Méthode analogue au c) ci-dessus.
$$\left\lbrace\begin{array}{lllllll} \text{Si }x&\leq&-\dfrac{4}{5}\;,&\text{alors}&f(x)&=&2x^{2}+5x-4\\ \text{Si }x&\geq&-\dfrac{4}{5}\;,&\text{alors}&f(x)&=&2x^{2}-5x+4 \end{array}\right.$$
D'où : $\lim_{\,x\rightarrow +\infty}f(x)=\lim_{\,x\rightarrow +\infty}(2x^{2}-5x+4)=\lim_{\,x\rightarrow +\infty}(2x^{2})=+\infty.$
Et : $\lim_{\,x\rightarrow -\infty}f(x)=\lim_{\,x\rightarrow -\infty}(2x^{2}+5x-4)=\lim_{\,x\rightarrow +\infty}(2x^{2})=+\infty.$
e) Par application du théorème sur la limite d'une fonction rationnelle à l'infini :
$\begin{array}{lcl}\ast\ \lim_{\,x\rightarrow +\infty}\left(\dfrac{2x^{2}-x}{x+3}\right)&=&\lim_{\,x\rightarrow +\infty}\left(\dfrac{2x^{2}}{x}\right)\\&=&\lim_{\,x\rightarrow +\infty}(2x)\\&=&+\infty.\end{array}$
$\begin{array}{lcl}\ast\ \lim_{\,x\rightarrow -\infty}\left(\dfrac{2x^{2}-x}{x+3}\right)&=&\lim_{\,x\rightarrow -\infty}\left(\dfrac{2x^{2}}{x}\right)\\&=&\lim_{\,x\rightarrow -\infty}(2x)\\&=&-\infty.\end{array}$
f) Par application du théorème sur la limite d'une fonction rationnelle à l'infini :
$\begin{array}{lcl}\ast\ \lim_{\,x\rightarrow +\infty}\left(\dfrac{x+1}{x^{2}+2}\right)&=&\lim_{\,x\rightarrow +\infty}\left(\dfrac{x}{x^{2}}\right)\\&=&\lim_{\,x\rightarrow +\infty}\left(\dfrac{1}{x}\right)\\&=&0.\end{array}$
$\begin{array}{lcl}\ast\ \lim_{\,x\rightarrow -\infty}\left(\dfrac{x+1}{x^{2}+2}\right)&=&\lim_{\,x\rightarrow -\infty}\left(\dfrac{x}{x^{2}}\right)\\&=&\lim_{\,x\rightarrow -\infty}\left(\dfrac{1}{x}\right)\\&=&0.\end{array}$
g) Par application du théorème sur la limite d'une fonction rationnelle à l'infini :
$\begin{array}{lcl}\ast\ \lim_{\,x\rightarrow +\infty}\left(\dfrac{x^{3}-3x}{x^{3}+x+2}\right)&=&\lim_{\,x\rightarrow +\infty}\left(\dfrac{x^{3}}{x^{3}}\right)\\&=&\lim_{\,x\rightarrow +\infty}(1)\\&=&1.\end{array}$
$\begin{array}{lcl}\ast\ \lim_{\,x\rightarrow -\infty}\left(\dfrac{x^{3}-3x}{x^{3}+x+2}\right)&=&\lim_{\,x\rightarrow -\infty}\left(\dfrac{x^{3}}{x^{3}}\right)\\&=&\lim_{\,x\rightarrow -\infty}(1)\\&=&1.\end{array}$
h) Attention, ici on n'a pas affaire à une fonction rationnelle.
Il est donc hors de question d'utiliser les « monômes » de plus haut degré.
On procède ainsi :
$\begin{array}{lcl}\ast\ \lim_{\,x\rightarrow +\infty}\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\right)&=&\lim_{\,x\rightarrow +\infty}\left(\dfrac{\sqrt{x}\left(1+\dfrac{1}{\sqrt{x}}\right)}{\sqrt{x}\left(1-\dfrac{1}{\sqrt{x}}\right)}\right)\\&=&\lim_{\,x\rightarrow +\infty}\dfrac{\left(1+\dfrac{1}{\sqrt{x}}\right)}{\left(1-\dfrac{1}{\sqrt{x}}\right)}\\&=&1\end{array}$
car $\lim_{x\rightarrow +\infty}\dfrac{1}{\sqrt{x}}=0.$
$\ast$ Cette fonction n'étant définie que pour $x\geq 0$ et $x\neq 1$(vérification laissée au lecteur), sa limite en $-\infty$ n'existe pas.
2) a) $\lim_{\,x\rightarrow 1}\left(\dfrac{1}{x-1}\right)$
Le graphique de signe de l'expression $(x-1)$ autour de $1$ est :
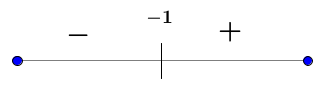
Il en résulte que : $\lim_{\,x\rightarrow 1^{+}}\left(\dfrac{1}{x-1}\right)=+\infty$ car $\left\lbrace\begin{array}{lcl} N&\rightarrow&1\\ D&\rightarrow&0^{+} \end{array}\right.$
où $N$ et $D$ désignent le numérateur et le dénominateur de la fonction.
De même, $\lim_{\,x\rightarrow 1^{-}}\left(\dfrac{1}{x-1}\right)=-\infty$ car $\left\lbrace\begin{array}{lcl} N&\rightarrow&1\\ D&\rightarrow&0^{+} \end{array}\right.$
b) $\lim_{\,x\rightarrow 2}\left(\dfrac{-3}{x^{2}-4}\right)$ et $\lim_{\,x\rightarrow -2}\left(\dfrac{-3}{x^{2}-4}\right)$
Le graphique de signe de l'expression $(x^{2}-4)$ autour de $-2$ et de $2$ est :
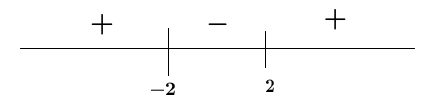
Il en résulte que : $\lim_{\,x\rightarrow (-2)^{+}}\left(\dfrac{-3}{x^{2}-4}\right)=-\infty$ car $\left\lbrace\begin{array}{lcl} N&\rightarrow&-3\\ D&\rightarrow&0^{-} \end{array}\right.$ et $\lim_{\,x\rightarrow (-2)^{+}}\left(\dfrac{-3}{x^{2}-4}\right)=+\infty$ car $\left\lbrace\begin{array}{lcl} N&\rightarrow&-3\\ D&\rightarrow&0^{-} \end{array}\right.$
De même, $\lim_{\,x\rightarrow 2^{+}}\left(\dfrac{-3}{x^{2}-4}\right)=-\infty$ car $\left\lbrace\begin{array}{lcl} N&\rightarrow&-3\\ D&\rightarrow&0^{+} \end{array}\right.$ et $\lim_{\,x\rightarrow 2^{-}}\left(\dfrac{-3}{x^{2}-4}\right)=+\infty$ car $\left\lbrace\begin{array}{lcl} N&\rightarrow&-3\\ D&\rightarrow&0^{-} \end{array}\right.$
c) $\lim_{\,x\rightarrow -3}\left(\dfrac{x^{2}+x+3}{(x+3)^{2}(-2)}\right)$ et $\lim_{\,x\rightarrow 2}\left(\dfrac{x^{2}+x+3}{(x+3)^{2}(x-2)}\right)$
Ici encore, on a affaire à une limite du type $''\dfrac{\text{réel}}{\text{zéro}}''$, donc il faut étudier le signe du dénominateur.
Le tableau de signe de l'expression $(x+3)^{2}(x-2)$ autour de $-3$ et de $2$ est :
$$\begin{array}{|c|lcccccr|} \hline x&-\infty& &-3& &2&+\infty&\\ \hline(x+3)^{2}& &+&|&+&|&+&\\ \hline (x-2)& &-&|&-&|&+&\\ \hline \text{Produit}& &-&|&-&|&+&\\ \hline \end{array}$$
Il en résulte que : $\lim_{\,x\rightarrow (-3)^{-}}\left(\dfrac{x^{2}+x+3}{(x+3)^{2}(x-2)}\right)=-\infty$ car $\left\lbrace\begin{array}{lcl} N&\rightarrow&9\\ D&\rightarrow&0^{-} \end{array}\right.$ et $\lim_{\,x\rightarrow (-3)^{+}}\left(\dfrac{x^{2}+x+3}{(x+3)^{2}(x-2)}\right)=-\infty$ car $\left\lbrace\begin{array}{lcl} N&\rightarrow&9\\ D&\rightarrow&0^{-} \end{array}\right.$
De même, $\lim_{\,x\rightarrow (2)^{+}}\left(\dfrac{x^{2}+x+3}{(x+3)^{2}(x-2)}\right)=-\infty$ car $\left\lbrace\begin{array}{lcl} N&\rightarrow&9\\ D&\rightarrow&0^{-} \end{array}\right.$ et $\lim_{\,x\rightarrow (2)^{-}}\left(\dfrac{x^{2}+x+3}{(x+3)^{2}(x-2)}\right)=+\infty$ car $\left\lbrace\begin{array}{lcl} N&\rightarrow&9\\ D&\rightarrow&0^{+} \end{array}\right.$
d) $\lim_{\,x\rightarrow(2k+1)\dfrac{\pi}{2}}(\tan x)$
Posons $x_{0}=(2k+1)\dfrac{\pi}{2}\;,\ (k\in\mathbb{Z})$
$\ast$ Si $k$ est pair, (nombres du type, $-\dfrac{3\pi}{2}$, $\dfrac{\pi}{2}$, $\dfrac{5\pi}{2}$, etc...) le cosinus est positif pour les valeurs de $x$ inférieures à $x_{0}$ et négatif pour les valeurs de $x$ supérieures à $x_{0}$ (le vérifier sur un graphique dans le cas de $\dfrac{\pi}{2}$ par exemple), tandis que le sinus tend vers $1.$
D'où : $\lim_{\,x\rightarrow x_{0}^{+}}\tan x=-\infty$ car $\left\lbrace\begin{array}{lcl} N&\rightarrow&1\\ D&\rightarrow&0^{-} \end{array}\right.$ et $\lim_{\,x\rightarrow x_{0}^{-}}\tan x=+\infty$ car $\left\lbrace\begin{array}{lcl} N&\rightarrow&1\\ D&\rightarrow&0^{+} \end{array}\right.$
$\ast$ Si $k$ est impair, (nombres du type, $-\dfrac{\pi}{2}$, $\dfrac{3\pi}{2}$, $\dfrac{7\pi}{2}$, etc...) le cosinus est négatif pour les valeurs de $x$ inférieures à $x_{0}$ et positif pour les valeurs de $x$ supérieures à $x_{0}$ (le vérifier sur un graphique dans le cas de $-\dfrac{\pi}{2}$ par exemple), tandis que le sinus tend vers $-1.$
D'où : $\lim_{\,x\rightarrow x_{0}^{+}}\tan x=-\infty$ car $\left\lbrace\begin{array}{lcl} N&\rightarrow&-1\\ D&\rightarrow&0^{+} \end{array}\right.$ et $\lim_{\,x\rightarrow x_{0}^{-}}\tan x=+\infty$ car $\left\lbrace\begin{array}{lcl} N&\rightarrow&1\\ D&\rightarrow&0^{-} \end{array}\right.$
Dans les deux cas, $\lim_{\,x\rightarrow x_{0}}\tan x$ n'existe pas !
e) $\lim_{\,x\rightarrow\pi}\left(\dfrac{2}{1+\cos x}\right)$
L'expression $(1+\cos x)$ est toujours positive car l'on a $-1\leq\cos x\leq 1$ pour tout réel $x.$
$\lim_{\,x\rightarrow\pi^{+}}\left(\dfrac{2}{1+\cos x}\right)=+\infty$ car $\left\lbrace\begin{array}{lcl} N&\rightarrow&2\\ D&\rightarrow&0^{+} \end{array}\right.$ et $\lim_{\,x\rightarrow\pi^{-}}\left(\dfrac{2}{1+\cos x}\right)=+\infty$ car $\left\lbrace\begin{array}{lcl} N&\rightarrow&2\\ D&\rightarrow&0^{+} \end{array}\right.$
On peut donc conclure que :$\lim_{\,x\rightarrow\pi}\left(\dfrac{2}{1+\cos x}\right)=+\infty.$
f) $\lim_{\,x\rightarrow-\dfrac{\pi}{6}}\left(\dfrac{3}{1+2\sin x}\right)$
Le graphique ci-dessous :
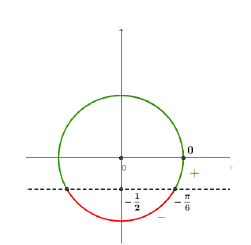
montre que l'on a $\sin x>-\dfrac{1}{2}$ (ou, ce qui est équivalent $2\sin x+1>0$) lorsque $x>-\dfrac{\pi}{6}$ et $\sin x<-\dfrac{1}{2}$ lorsque $x<-\dfrac{\pi}{6}.$
Par conséquent, le dénominateur de l'expression $\dfrac{3}{1+2\sin x}$ tend vers $0^{-}$ lorsque $x$ tend vers $\left(-\dfrac{\pi}{6}\right)$ par valeurs inférieures et vers $0^{+}$ lorsque $x$ tend vers $\left(-\dfrac{\pi}{6}\right)$ par valeurs supérieures.
Le calcul suivant en découle :
$\lim_{\,x\rightarrow\left(-\dfrac{\pi}{6}\right)^{-}}\left(\dfrac{3}{1+2\sin x}\right)=-\infty$ car $\left\lbrace\begin{array}{lcl} N&\rightarrow&3\\ D&\rightarrow&0^{-} \end{array}\right.$ et $\lim_{\,x\rightarrow\left(-\dfrac{\pi}{6}\right)^{+}}\left(\dfrac{3}{1+2\sin x}\right)=-\infty$ car $\left\lbrace\begin{array}{lcl} N&\rightarrow&3\\ D&\rightarrow&0^{+} \end{array}\right.$
3) a) $f\ :\ x\mapsto\dfrac{1-\cos x}{x^{2}-2x|x|}\quad x_{0}=0$
On a : $f(x)=\left\lbrace\begin{array}{ll} \dfrac{1-\cos x}{3x^{2}}&\text{si }<0\\ \\ \dfrac{1-\cos x}{-x^{2}}&\text{si }\geq 0 \end{array}\right.$
Par suite, en utilisant la limite usuelle : $\lim_{\,x\rightarrow 0}\left(\dfrac{1-\cos x}{x^{3}}\right)=\dfrac{1}{2}$ on obtient :
$\lim_{\,x\rightarrow 0^{-}}f(x)=\lim_{\,x\rightarrow 0^{-}}\left(\dfrac{1}{3}\times\dfrac{1-\cos x}{x^{2}}\right)$, soit $\lim_{\,x\rightarrow 0^{-}}f(x)=\dfrac{1}{6}.$
Et de manière analogue $\lim_{\,x\rightarrow 0^{+}}f(x)=-\dfrac{1}{2}.$
b) $f\ :\ x\mapsto\left\lbrace\begin{array}{ll} x^{2}-1\;,&x\leq 0\\ x^{2}+1\;,&x>0\quad x_{0}=0 \end{array}\right.$
$\lim_{\,x\rightarrow 0^{-}}f(x)=\lim_{\,x\rightarrow 0^{-}}(x^{2}-1)=-1$ et $\lim_{\,x\rightarrow 0^{+}}f(x)=\lim_{\,x\rightarrow 0^{+}}(x^{2}+1)=1.$
c) $f\ :\ x\mapsto\dfrac{x^{2}+x}{\sqrt{x^{2}}}\quad x_{0}=0$
On a pour tout $x$ non nul, $\sqrt{x^{2}}=|x|$, d'où
$\begin{array}{lcl}\lim_{\,x\rightarrow 0^{-}}f(x)&=&\lim_{\,x\rightarrow 0^{-}}\left(\dfrac{x^{2}+x}{-x}\right)\\&=&\lim_{\,x\rightarrow 0^{-}}(-x+1)\\&=&-1 \end{array}$
et $\begin{array}{lcl}\lim_{\,x\rightarrow 0^{+}}f(x)&=&\lim_{\,x\rightarrow 0^{+}}\left(\dfrac{x^{2}+x}{x}\right)\\&=&\lim_{\,x\rightarrow 0^{+}}(x+1)\\&=&1 \end{array}$
d) $f\ :\ x\mapsto\dfrac{|2x+1|}{2x+1}\quad x_{0}=-\dfrac{1}{2}$
On a : $f(x)=\left\lbrace\begin{array}{lcl} -1\text{ si }x&<&-\dfrac{1}{2}\\ \\ 1\text{ si }x&>&-\dfrac{1}{2} \end{array}\right.$,
D'où : $\lim_{\,x\rightarrow\left(-\dfrac{1}{2}\right)^{+}}f(x)=1$ et $\lim_{\,x\rightarrow\left(-\dfrac{1}{2}\right)^{-}}f(x)=-1.$
e) $f\ :\ x\mapsto x\sqrt{(x-1)^{2}}\quad x_{0}=1$
On a : $f(x)=x|x-1|=\left\lbrace\begin{array}{ll} x(-x+1)&\text{si }x\leq 1\\ x(x-1)&\text{si }\geq 1 \end{array}\right.$
On a $\lim_{\,x\rightarrow 0^{-}}f(x)=\lim_{\,x\rightarrow 0^{+}}f(x)=0.$
$\begin{array}{lcl}9)\quad\lim_{\,x\rightarrow 0}f(x)&=&\lim_{\,x\rightarrow 0}\left[\dfrac{\tan 2x}{\sqrt{1-\cos x}}\right]\\&=&\lim_{\,x\rightarrow 0}\left[\dfrac{\tan 2x}{\sqrt{2\sin^{2}\left(\dfrac{x}{2}\right)}}\right]\\&=&\lim_{\,x\rightarrow 0}\left[\dfrac{\tan 2x}{\sqrt{2}\times|\sin\left(\dfrac{x}{2}\right)|}\right].\end{array}$
Levée l'indétermination
Exercice 4
1) $f\ :\ x\mapsto\dfrac{x^{3}+3x-4}{x-1}\text{ en }1\;,\ -\infty\;,\ +\infty$
$D_{f}=\mathbb{R}\setminus{1}=]-\infty\;;\ 1[\cup]1\;;\ +\infty[$
$\bullet$ Le calcul de la limite de $f$ en $1$ se présente a priori sous la forme d'une indétermination du type « $\dfrac{0}{0}$ », car lorsque $x$ tend vers $1$, aussi bien le numérateur que le dénominateur de la fraction $f(x)$ tendent vers $0.$
On cherche donc à factoriser le numérateur et le dénominateur qui sont des polynômes ayant une racine commune, à savoir, $1.$
Par la méthode de Hörner ou la division euclidienne, on obtient facilement pour le numérateur : $x^{3}+3x-4=(x-1)(x^{2}+x+4).$
D'où, en simplifiant : $\lim_{\,x\rightarrow 1}f(x)=\lim_{\,x\rightarrow 1}(x^{2}+x+4)=6.$
$\bullet$ Pour les limites en $+\infty$ et en $-\infty$, on utilise le théorème relatif à la limite d'une fonction rationnelle à l'infini :
$\begin{array}{lcl}\lim_{\,x\rightarrow -\infty}f(x)&=&\lim_{\,x\rightarrow -\infty}\left(\dfrac{x^{3}}{x}\right)\\&=&\lim_{\,x\rightarrow -\infty}(x^{2})\\&=&+\infty\end{array}$
$\begin{array}{lcl}\lim_{\,x\rightarrow +\infty}f(x)&=&\lim_{\,x\rightarrow +\infty}\left(\dfrac{x^{3}}{x}\right)\\&=&\lim_{\,x\rightarrow +\infty}(x^{2})\\&=&+\infty\end{array}$
2) $f\ :\ x\mapsto\dfrac{x^{2}+4x+4}{x^{2}+8}\text{ en }-2\;,\ -\infty\;,\ +\infty$
Méthodes analogues à celles du 1) précédent.
$\begin{array}{lcl}\ast\ \lim_{\,x\rightarrow -2}f(x)&=&\lim_{\,x\rightarrow -2}\left[\dfrac{(x+2)^{2}}{(x+2)(x^{2}-x+4)}\right]\\&=&\lim_{\,\rightarrow -2}\left[\dfrac{(x+2)}{(x^{2}-x+4)}\right]\\&=&0\end{array}$
car $\left\lbrace\begin{array}{lcl} N&\rightarrow& 0\\ D&\rightarrow& 10 \end{array}\right.$
$\begin{array}{lcl}\ast\ \lim_{\,x\rightarrow -\infty}f(x)&=&\lim_{\,x\rightarrow -\infty}\left(\dfrac{x^{2}}{x^{3}}\right)\\&=&\lim_{\,x\rightarrow -\infty}\left(\dfrac{1}{x}\right)\\&=&0\end{array}$
$\begin{array}{lcl}\ast\ \lim_{\,x\rightarrow +\infty}f(x)&=&\lim_{\,x\rightarrow +\infty}\left(\dfrac{x^{2}}{x^{3}}\right)\\&=&\lim_{\,x\rightarrow +\infty}\left(\dfrac{1}{x}\right)\\&=&0\end{array}$
3) $f\ :\ x\mapsto\sqrt{1+x^{2}}-x\text{ en }-\infty\;,\ +\infty$
$\bullet$ En $-\infty$, le calcul de la limite ne présente pas d'indétermination car : $\left\lbrace\begin{array}{lcl} \lim_{\,x\rightarrow -\infty}(1+x^{2})&=&+\infty\text{ et }\\ \lim_{\,x\rightarrow +\infty}\sqrt{x}&=&+\infty \end{array}\right.$
d'où, par composition : $\lim_{\,x\rightarrow -\infty}\sqrt{1+x^{2}}=+\infty\quad(1)\text{ et }\lim_{\,x\rightarrow -\infty}(-x)=+\infty\quad(2)$
Par somme, on en déduit alors que : $\lim_{\,x\rightarrow -\infty}=+\infty$
$\bullet$ En $+\infty$, on a une indétermination du type « $+\infty\;-\infty$ ».
On utilise l'expression conjuguée pour la lever.
$\begin{array}{lcl}\lim_{\,x\rightarrow +\infty}f(x)&=&\lim_{\,x\rightarrow +\infty}\left[\dfrac{(\sqrt{1+x^{2}}-x)(\sqrt{1+x^{2}}+x)}{(\sqrt{1+x^{2}}+x)}\right]\\&=&\lim_{\,x\rightarrow +\infty}\left[\dfrac{1+x^{2}-x^{3}}{(\sqrt{1+x^{2}}+x)}\right]\\&=&\lim_{\,x\rightarrow +\infty}\left[\dfrac{1}{(\sqrt{1+x^{2}}+x)}\right]\end{array}$
Or, on a : $\left\lbrace\begin{array}{lcl} \lim_{\,x\rightarrow +\infty}(1+x^{2})&=&+\infty\text{ et }\\ \lim_{\,x\rightarrow +\infty}\sqrt{x}&=&+\infty \end{array}\right.$
d'où, par composition :
$\lim_{\,x\rightarrow +\infty}\sqrt{1+x^{2}}=+\infty\quad(3)$
et $\lim_{\,x\rightarrow +\infty}(x)=+\infty\quad(4).$
Par somme, on en déduit alors que : $\lim_{\,x\rightarrow +\infty}(\sqrt{1+x^{2}}+x)=+\infty.$
On en conclut alors que $\begin{array}{lcl}\lim_{\,x\rightarrow +\infty}f(x)&=&\lim_{\,x\rightarrow +\infty}\left[\dfrac{1}{(\sqrt{1+x^{2}}+x)}\right]\\&=&0\end{array}$
car $\left\lbrace\begin{array}{lcl} N&\rightarrow& 1\\ D&\rightarrow& +\infty \end{array}\right.$
4) $f\ :\ x\mapsto\dfrac{\sqrt{3+x}-2x}{x-1}\text{ en }1\;,\ +\infty$
On vérifie aisément que $D_{f}=[-3\;;\ 1[\cup]1\;;\ +\infty[.$
$\bullet$ En $1$, on a une indétermination du type « $\dfrac{0}{0}$ ».
On la lève en multipliant numérateur et dénominateur par l'expression conjuguée du numérateur :
$\begin{array}{lcl} \lim_{\,x\rightarrow 1}f(x)&=&\lim_{\,x\rightarrow 1}\left[\dfrac{(\sqrt{3+x}-2x)(\sqrt{3+x}+2x)}{(x-1)(\sqrt{3+x}+2x)}\right]\\&=&\lim_{\,x\rightarrow 1}\left[\dfrac{3+x-4x^{2}}{(x-1)(\sqrt{3+x}+2x}\right] \end{array}$
Le numérateur de cette dernière expression est un trinôme du second degré qui a pour racines $1$ et $-\dfrac{3}{4}.$
Il se factorise donc en $-4(x-1)\left(x+\dfrac{3}{4}\right)$ ou encore en $(x-1)(-4x-3).$
$\begin{array}{lcl}\text{Ainsi}\quad\lim_{\,x\rightarrow 1}f(x)&=&\lim_{\,x\rightarrow 1}\left[\dfrac{(x-1)(-4x-3)}{(x-1)(\sqrt{3+x}+2x)}\right]\\&=&\lim_{\,x\rightarrow 1} \left[\dfrac{(-4x-3)}{(\sqrt{3+x}+2x)}\right]\\&=&-\dfrac{7}{4} \end{array}$
car $\left\lbrace\begin{array}{lcl} N&\rightarrow& -7\\ D&\rightarrow& 4 \end{array}\right.$
$\bullet$ En $+\infty$, on a, en factorisant par $x$, au numérateur et au dénominateur :
$\begin{array}{lcl} \lim_{\,x\rightarrow +\infty}f(x)&=&\lim_{\,x\rightarrow +\infty}\dfrac{x\left(-2+\dfrac{\sqrt{3+x}}{x}\right)}{x\left(1-\dfrac{1}{x}\right)}\\&=&\lim_{\,x\rightarrow +\infty}\dfrac{-2+\dfrac{\sqrt{3+x}}{x}}{\left(1-\dfrac{1}{x}\right)} \end{array}$
Or $\lim_{\,x\rightarrow +\infty}\left[\dfrac{\sqrt{3+x}}{x}\right]=\lim_{\,x\rightarrow +\infty}\left[\sqrt{\dfrac{3+x}{x^{2}}}\right]$ (car au voisinage de $+\infty$, on a $x=\sqrt{x^{2}}).$
$\begin{array}{lcl}\text{Et les relations}\quad\lim_{\,x\rightarrow +\infty}\left(\dfrac{3+x}{x^{2}}\right)&=&\lim_{\,x\rightarrow +\infty}\left(\dfrac{x}{x^{2}}\right)\\&=&\lim_{\,x\rightarrow +\infty}\left(\dfrac{1}{x}\right)\\&=&0 \end{array}$
Limite d'une fonction trigonométrique en $0$
Exercice 5
$\begin{array}{lcl}1)\quad\lim_{\,x\rightarrow 0}f(x)&=&\lim_{\,x\rightarrow 0}\left[\dfrac{\sin 5x}{2x}\right]\\&=&\lim_{\,x\rightarrow 0}\left[\dfrac{\sin 5x}{5x}\times\dfrac{5x}{2x}\right]\\&=&1\times\dfrac{5}{2}\\&=&\dfrac{5}{2}.\end{array}$
$\begin{array}{lcl}2)\quad\lim_{\,x\rightarrow 0}f(x)&=&\lim_{\,x\rightarrow 0}\left[\dfrac{x}{\sin 3x}\right]\\&=&\lim_{\,x\rightarrow 0}\left[\dfrac{x}{3x}\times\dfrac{3x}{\sin 3x}\right]\\&=&1\times\dfrac{1}{3}\\&=&\dfrac{1}{3}.\end{array}$
$\begin{array}{lcl}3)\quad\lim_{\,x\rightarrow 0}f(x)&=&\lim_{\,x\rightarrow 0}\left[\dfrac{\sin 5x}{\sin 4x}\right]\\&=&\lim_{\,x\rightarrow 0}\left[\dfrac{\sin 5x}{5x}\times\dfrac{5x}{4x}\times\dfrac{4x}{\sin 4x}\right]\\&=&1\times\dfrac{5}{4}\times 1\\&=&\dfrac{5}{4}.\end{array}$
$\begin{array}{lcl}4)\quad\lim_{\,x\rightarrow 0}f(x)&=&\lim_{\,x\rightarrow 0}\left[\dfrac{\tan x}{x}\right]\\&=&\lim_{\,x\rightarrow 0}\left[\dfrac{\sin x}{x}\times\dfrac{1}{\cos x}\right]\\&=&1\times\dfrac{1}{1}\\&=1&.\end{array}$
$\begin{array}{lcl}5)\quad\lim_{\,x\rightarrow 0}f(x)&=&\lim_{\,x\rightarrow 0}\left[\dfrac{\tan 2x}{\sin x}\right]\\&=&\lim_{\,x\rightarrow 0}\left[\dfrac{\tan 2x}{2x}\times\dfrac{2x}{x}\times\dfrac{x}{\sin x}\right]\\&=&1\times 2\times 1\\&=&2.\end{array}$
$\begin{array}{lcl}6)\quad\lim_{\,x\rightarrow 0}f(x)&=&\lim_{\,x\rightarrow 0}\left[\dfrac{\sin x}{\sqrt{x}}\right]\\&=&\lim_{\,x\rightarrow 0}\left[\dfrac{\sin x}{x}\times\dfrac{x}{\sqrt{x}}\right]\\&=&\left[\dfrac{\sin x}{x}\times\sqrt{x}\right]\\&=&1\times 0\\&=&0.\end{array}$
$\begin{array}{lcl}7)\quad\lim_{\,x\rightarrow 0}f(x)&=&\lim_{\,x\rightarrow 0}\left[\dfrac{1-\cos x}{x^{2}}\right]\\&=&\lim_{\,x\rightarrow 0}\left[\dfrac{2\sin^{2}\left(\dfrac{x}{2}\right)}{4\times\left(\dfrac{x}{2}\right)^{2}}\right]\\&=&\lim_{\,x\rightarrow 0}\left[\dfrac{1}{2}\times\left(\dfrac{\sin\left(\dfrac{x}{2}\right)^{2}}{\left(\dfrac{x}{2}\right)}\right)^{2}\right]\\&=&\dfrac{1}{2}\times 1^{2}\\&=&\dfrac{1}{2}.\end{array}$
$\begin{array}{lcl}8)\quad\lim_{\,x\rightarrow 0}f(x)&=&\lim_{\,x\rightarrow 0}\left[\dfrac{1-\cos x}{x^{2}}\right]\\&=&\lim_{\,x\rightarrow 0}\left[-\dfrac{2\sin^{2}(2x)}{x^{2}}\right]\\&=&\lim_{\,x\rightarrow 0}\left[\dfrac{-2\sin^{2}(2x)}{4x^{2}}\times 4\right]\\&=&\lim_{\,x\rightarrow 0}\left[-8\times\left(\dfrac{\sin(2x)}{(2x)}\right)^{2}\right]\\&=&-8\times 1^{2}\\&=&-8\end{array}$
$\begin{array}{lcl}9)\quad\lim_{\,x\rightarrow 0}f(x)&=&\lim_{\,x\rightarrow 0}\left[\dfrac{\tan 2x}{\sqrt{1-\cos x}}\right]\\&=&\lim_{\,x\rightarrow 0}\left[\dfrac{\tan 2x}{\sqrt{2\sin^{2}\left(\dfrac{x}{2}\right)}}\right]\\&=&\lim_{\,x\rightarrow 0}\left[\dfrac{\tan 2x}{\sqrt{2}\times|\sin\left(\dfrac{x}{2}\right)|}\right].\end{array}$
Il y a lieu de distinguer deux cas :
$\begin{array}{lcl}\lim_{\,x\rightarrow 0^{+}}f(x)&=&\lim_{\,x\rightarrow 0^{+}}\left[\dfrac{\tan 2x}{\sqrt{2}\times\sin\left(\dfrac{x}{2}\right)}\right]\\&=&\lim_{\,x\rightarrow 0^{+}}\left[\dfrac{1}{\sqrt{2}}\times\dfrac{\tan 2x}{2x}\times\dfrac{2x}{\dfrac{x}{2}}\times\dfrac{\dfrac{x}{2}}{\sin\left(\dfrac{x}{2}\right)}\right]\\&=&\dfrac{1}{\sqrt{2}}\times 1\times 4\times 1\\&=&\dfrac{4}{\sqrt{2}}\\&=&2\sqrt{2}.\end{array}$
$\begin{array}{lcl}\lim_{\,x\rightarrow 0^{-}}f(x)&=&\lim_{\,x\rightarrow 0^{-}}\left[\dfrac{\tan 2x}{-\sqrt{2}\times\sin\left(\dfrac{x}{2}\right)}\right]\\&=&\lim_{\,x\rightarrow 0^{-}}\left[-\dfrac{1}{\sqrt{2}}\times\dfrac{\tan 2x}{2x}\times\dfrac{2x}{\dfrac{x}{2}}\times\dfrac{\dfrac{x}{2}}{\sin\left(\dfrac{x}{2}\right)}\right]\\&=&-\dfrac{1}{\sqrt{2}}\times 1\times 4\times 1\\&=&-\dfrac{4}{\sqrt{2}}\\&=&-2\sqrt{2}.\end{array}$
$\begin{array}{lcl}10)\quad\lim_{\,x\rightarrow 0}f(x)&=&\lim_{\,x\rightarrow 0}\left[\dfrac{1-\cos x}{\sin^{2}\pi x}\right]\\&=&\lim_{\,x\rightarrow 0}\left[\dfrac{2\sin^{2}\left(\dfrac{x}{2}\right)}{\sin^{2}\pi x}\right]\\&=&\lim_{\,x\rightarrow 0}\left[\dfrac{2\sin^{2}\left(\dfrac{x}{2}\right)}{\left(\dfrac{x}{2}\right)^{2}}\times\dfrac{\left(\dfrac{x}{2}\right)^{2}}{(\pi x)^{2}}\times\dfrac{(\pi x)^{2}}{\sin^{2}\pi x}\right]\\&=&\lim_{\,x\rightarrow 0}\left[\dfrac{2\sin^{2}\left(\dfrac{x}{2}\right)}{\left(\dfrac{x}{2}\right)^{2}}\times\dfrac{1}{4\pi^{2}}\times\left(\dfrac{\pi x}{\sin\pi x}\right)^{2}\right]\\&=&2\times 1^{2}\times\dfrac{1}{4\pi^{2}}\times 1^{2}\\&=&\dfrac{1}{2\pi^{2}}.\end{array}$
Il y a lieu de distinguer deux cas :
Limite d'une fonction trigonométrique en $x_{0}$
Exercice 6
1) $f\ :\ x\mapsto\dfrac{\sin(2x-\pi)}{\tan(2x-\pi)}\quad x_{0}=\dfrac{\pi}{2}$
Posant $X=x-\dfrac{\pi}{2}$, on obtient :
$\begin{array}{lcl}\lim_{\,x\rightarrow\dfrac{\pi}{2}}\dfrac{\sin(2x-\pi)}{\tan(2x-\pi)}&=&\lim_{\,X\rightarrow 0}\dfrac{\sin 2X}{\tan 2X}\\&=&\lim_{\,X\rightarrow 0}\dfrac{\sin 2X}{2X}\times\dfrac{2X}{\tan 2X}\end{array}$
Les quantités $\dfrac{\sin 2X}{2X}$ et $\dfrac{2X}{\tan 2X}$ tendant tous deux vers $1$ lorsque $X$ tend vers $0$, (voir exercice précédent) il est clair que :
$$\lim_{\,x\rightarrow\dfrac{\pi}{2}}\dfrac{\sin(2x-\pi)}{\tan(2x-\pi)}=1.$$
2) $f\ :\ x\mapsto\dfrac{\sin 6x}{2\cos x-\sqrt{3}}\quad x_{0}=\dfrac{\pi}{6}$
Posons $X=x-\dfrac{\pi}{6}.$
Alors $x=X+\dfrac{\pi}{6}.$
$\begin{array}{lcl}\lim_{\,X\rightarrow\dfrac{\pi}{6}}\dfrac{\sin 6x}{2\cos x-\sqrt{3}}&=&\lim_{\,X\rightarrow 0}\dfrac{\sin 6\left(X+\dfrac{\pi}{6}\right)}{2\cos\left(X+\dfrac{\pi}{6}\right)-\sqrt{3}}\\&=&\lim_{\,X\rightarrow 0}\dfrac{\sin(6X+\pi)}{2\left(\cos X\cos\dfrac{\pi}{6}-\sin X\dfrac{\pi}{6}\right)-\sqrt{3}}\\&=&\lim_{\,X\rightarrow 0}\dfrac{\sin 2X}{\sqrt{3}\cos X-\sin X-\sqrt{3}}\\&=&lim_{\,X\rightarrow 0}\dfrac{\sin 2X}{\sqrt{3}(\cos X-1)-\sin X}\\&=&\lim_{\,X\rightarrow 0}\dfrac{2\sin X\cos X}{\sqrt{3}\left(-2\sin^{2}\dfrac{X}{2}\right)-2\sin\dfrac{X}{2}\cos\dfrac{X}{2}}\\&=&\lim_{\,X\rightarrow 0}\dfrac{4\sin\dfrac{X}{2}\cos\dfrac{X}{2}\cos X}{-2\sin\dfrac{X}{2}\left(\sqrt{3}\sin\dfrac{X}{2}+\cos\dfrac{X}{2}\right)}\\&=&\dfrac{4\times 1\times 1}{-2(\sqrt{3}\times 0+1)}\\&=&-2.\end{array}$
3) $f\ :\ x\mapsto\dfrac{\tan x}{\sin 2x-1}\quad x_{0}=\dfrac{\pi}{4}$
On a $\lim_{\,x\rightarrow\dfrac{\pi}{4}}\tan x=1\text{ et }\lim_{\,x\rightarrow\dfrac{\pi}{4}}(\sin 2x-1)=0^{-}.$
D'où $\lim_{\,x\rightarrow\dfrac{\pi}{4}}\dfrac{\tan x}{\sin 2x-1}=-\infty.$
Morale : il faut toujours vérifier si l'on a bien affaire à une forme indéterminée avant de se lancer « tête baissée » dans les calculs.
Déterminer une limite par lecture graphique
Exercice 7
1) $D_{f}=\mathbb{R}\setminus{0}$ (on n'a pas indiqué si le point d'abscisse $0$ fait partie de la courbe).
2) $\lim_{\,x\rightarrow 0^{-}}f(x)=+\infty\;;\ \lim_{\,x\rightarrow 0^{+}}f(x)=0$ (voir l'allure de la courbe au voisinage de $0$);
$\lim_{\,x\rightarrow +\infty}f(x)=+\infty$ (car $\mathcal{C}_{f}$ est asymptote à la droite d'équation $y=\dfrac{3}{5}x$ au voisinage de $+\infty$ et $\lim_{\,x\rightarrow +\infty}\left(\dfrac{3}{5}x\right)=+\infty)$
$\lim_{\,x\rightarrow -\infty}f(x)=2$ (car $\mathcal{C}_{f}$ admet pour asymptote horizontale la droite d'équation $y=2$ au voisinage de $-\infty).$
Exercice 8
Déterminons tout d'abord une équation de la droite $\Delta.$
Elle est visiblement de la forme $y=ax+b.$
Puisqu'elle passe par le point de coordonnées $(0\;;\ 1)$, on a $b=1$ et elle passe par exemple par le point de coordonnées $(1\;;\ 2)$, donc on a aussi : $2=a+1\Rightarrow a=1.$
Finalement l'équation réduite de $\Delta$ est : $y=x+1.$
$\ast\ \lim_{\,x\rightarrow +\infty}f(x)=+\infty$ (car $\mathcal{C}_{f}$ est asymptote à la droite d'équation $y=x+1$ au voisinage de $+\infty$ et $\lim_{\,x\rightarrow +\infty}(x+1)=+\infty$)
$\ast\ \lim_{\,x\rightarrow -\infty}f(x)=0$ (car $\mathcal{C}_{f}$ admet pour asymptote horizontale l'axe des abscisses $(y=0)$ au voisinage de $-\infty).$
$\ast\ \lim_{\,x\rightarrow 0^{-}}f(x)=+\infty$ (voir l'allure de la courbe au voisinage de $0$ à gauche) ;
$\ast$ Puisque $f$ admet pour asymptote oblique la droite $\Delta$ d'équation $y=x+1$, on a $\lim_{\,x\rightarrow +\infty}\dfrac{f(x)}{x}=1.$
Exercice 9
a) $\lim_{\,x\rightarrow -\infty}f(x)=1$ (car $\mathcal{C}_{f}$ admet pour asymptote horizontale la droite d'équation $y=1$ au voisinage de $-\infty).$
$\lim_{\,x\rightarrow +\infty}f(x)=+\infty$ (car $\mathcal{C}_{f}$ est asymptote à la droite d'équation $y=x$ au voisinage de $+\infty$ et $\lim_{\,x\rightarrow +\infty}f(x)=+\infty$)
b) $\lim_{\,x\rightarrow 0^{-}}f(x)=+\infty$ ; $\lim_{\,x\rightarrow 0^{+}}f(x)=+\infty$ (voir l'allure de la courbe au voisinage de $0$) ;
c) $\lim_{\,x\rightarrow +\infty}[f(x)-x]=0$ (puisque, par hypothèse, la droite d'équation $y=x$ est une asymptote à la courbe au voisinage de $+\infty).$
d) Quand $x$ tend vers $\alpha$ par valeurs inférieures, $f(x)$ tend vers $0$ mais en restant positif.
On en déduit que :
$\lim_{\,x\rightarrow \alpha^{+}}\dfrac{1}{f(x)})=+\infty$ car $\left\lbrace\begin{array}{lcl} N&\rightarrow& 1\\ D&\rightarrow & 0^{+} \end{array}\right.$
e) Quand $x$ tend vers $\alpha$ par valeurs supérieures, $f(x)$ tend vers $0$ mais en restant négatif.
On en déduit que :
$\lim_{\,x\rightarrow \alpha^{-}}\dfrac{1}{f(x)})=-\infty$ car $\left\lbrace\begin{array}{lcl} N&\rightarrow& 1\\ D&\rightarrow & 0^{-} \end{array}\right.$
Limite d'une fonction composée
Exercice 10
1) $f\ :\ x\mapsto\cos\dfrac{\pi(x+1)}{x}$
Posons $u(x)=\dfrac{\pi(x+1)}{x}$ et $v(x)=\cos x.$
Les relations $\lim_{\,x\rightarrow +\infty}u(x)=\pi$ et $\lim_{\,x\rightarrow \pi}v(x)=-1$, entraînent, d'après le théorème sur la limite d'une fonction composée, que :
$\lim_{\,x\rightarrow +\infty}\left[\cos\dfrac{\pi(x+1)}{x}\right]=-1.$
2) $f\ :\ x\mapsto\sqrt{\dfrac{2x^{2}-1}{x}}$
Posons $u(x)=\dfrac{2x^{2}-1}{x}$ et $v(x)=\sqrt{x}.$
Les relations $\lim_{\,x\rightarrow +\infty}u(x)=\lim_{\,x\rightarrow +\infty}\dfrac{2x^{2}}{x}=\lim_{\,x\rightarrow +\infty}2x=+\infty$ et $\lim_{\,x\rightarrow +\infty}v(x)=+\infty$, entraînent, d'après le théorème sur la limite d'une fonction composée, que :
$\lim_{\,x\rightarrow +\infty}u(x)=\left[\sqrt{\dfrac{2x^{2}-1}{x}}\right]=+\infty.$
3) $f\ :\ x\mapsto\sin\dfrac{1}{\sqrt{x}}\text{ en }+\infty$
Posons $u(x)=\dfrac{1}{\sqrt{x}}$ et $v(x)=\sin x.$
Les relations $\lim_{\,x\rightarrow +\infty}u(x)=0$ et $\lim_{\,x\rightarrow 0}\sin x=0$, entraînent, d'après le théorème sur la limite d'une fonction composée, que :
$\lim_{\,x\rightarrow +\infty}\left[\sin\dfrac{1}{\sqrt{x}}\right]=0.$
4) $f\ :\ x\mapsto\dfrac{1-\sqrt{|x|}}{2+\sqrt{|x|}}\text{ en }-\infty$
Posons $u(x)=\dfrac{x-1}{2+x}$, $v(x)=\sqrt{x}$ et $w(x)=|x|.$
On vérifie aisément les relations
$\lim_{\,x\rightarrow -\infty}w(x)=+\infty$, $\lim_{\,x\rightarrow +\infty}v(x)=+\infty$ et $\lim_{\,x\rightarrow +\infty}u(x)=\lim_{\,x\rightarrow +\infty}\dfrac{-x}{x}=1.$
D'où, d'après le théorème sur la limite d'une fonction composée (ici il y en a trois) : $$\lim_{\,x\rightarrow +\infty}\left[\dfrac{1-\sqrt{|x|}}{2+\sqrt{|x|}}\right]=-1.$$
5) $f\ :\ x\mapsto\sqrt{\dfrac{2x+1}{x-3}}\text{ en }+\infty$
Posons $u(x)=\dfrac{2x+1}{x-3}$ et $v(x)=\sqrt{x}.$
Les relations $\lim_{\,x\rightarrow +\infty}u(x)=\lim_{\,x\rightarrow +\infty}\dfrac{2x}{x}=2$ et $\lim_{\,x\rightarrow 2}v(x)=\sqrt{2}$, entraînent, d'après le théorème sur la limite d'une fonction composée, que :
$\lim_{\,x\rightarrow +\infty}\left[\sqrt{\dfrac{2x+1}{x-3}}\right]=\sqrt{2}.$
6) $f\ :\ x\mapsto\sqrt{\dfrac{2x+1}{x-3}}\text{ en }-\dfrac{1}{2}\;,\text{ puis en }3$
Notons d'abord que la fonction $f$ n'est définie que si $x\neq 3$ et si $\dfrac{2x+1}{x-3}\geq 0.$
En tenant compte de ces deux conditions, on voit facilement que $D_{f}=\left]-\infty\;;\ -\dfrac{1}{2}\right]\cup]3\;;\ +\infty[.$
$\ast$ En $-\dfrac{1}{2}$ :
Avec les notations de la question précédente, on a :
$\lim_{\,x\rightarrow -\dfrac{1}{2}}u(x)=0$ et $\lim_{\,x\rightarrow 0}v(x)=0.$
d'où, d'après le théorème sur la limite d'une fonction composée :$$\lim_{\,x\rightarrow -\dfrac{1}{2}}\left(\sqrt{\dfrac{2x+1}{x-3}}\right)=0.$$
$\ast$ En $3$ :
Avec les notations de la question précédente, on a :
$\lim_{\,x\rightarrow 3^{+}}u(x)=+\infty$ (car le numérateur de $u(x)$ tend vers $3$ tandis que son dénominateur tend vers $0^{+}$) et $\lim_{\,x\rightarrow +\infty}v(x)=+\infty$, d'où, d'après le théorème sur la limite d'une fonction composée : $$\lim_{\,x\rightarrow -\dfrac{1}{2}}\left(\sqrt{\dfrac{2x+1}{x-3}}\right)=+\infty.$$
7) $f\ :\ x\mapsto\sqrt{\dfrac{1}{x^{2}-1}}\text{ en }-1\;,\ 1\;,\ -\infty\;,\ + \infty$
$f(x)$ existe si et seulement si $\dfrac{1}{x^{2}-1}>0.$
$D_{f}=]-\infty\;;\ -1[\cup]1\;;\ +\infty[$
$\ast$ En $-1$ :
Posons $u(x)=\dfrac{1}{x^{2}-1}$ et $v(x)=\sqrt{x}.$
On a $\lim_{\,x\rightarrow(-1)^{-}}u(x)=+\infty$
car $\left\lbrace\begin{array}{lcl} N&\rightarrow &1\\ D&\rightarrow&0^{+} \end{array}\right.$ et $\lim_{\,x\rightarrow +\infty}v(x)=+\infty$,
d'où, d'après le théorème sur la limite d'une fonction composée :
$$\lim_{\,x\rightarrow(-1)^{-}}\left(\sqrt{\dfrac{1}{x^{2}-1}}\right)=+\infty$$
$\ast$ En $1$ :
Avec les notations de la question précédente, on a :
$\lim_{\,x\rightarrow 1^{+}}u(x)=+\infty$ (car le numérateur de $u(x)$ tend vers $1$ tandis que son dénominateur tend vers $0^{+}$)
et $\lim_{\,x\rightarrow +\infty}v(x)=+\infty$, d'où, d'après le théorème sur la limite d'une fonction composée :
$$\lim_{\,x\rightarrow -\dfrac{1}{2}}\left(\sqrt{\dfrac{1}{x^{2}-1}}\right)=+\infty.$$
$\ast$ En $-\infty$ :
Avec les notations de la question précédente, on a :
$\lim_{\,x\rightarrow -\infty}u(x)=\lim_{\,x\rightarrow -\infty}\left(\dfrac{1}{x^{2}}\right)=0$
et $\lim_{\,x\rightarrow 0}v(x)=0$, d'où, d'après le théorème sur la limite d'une fonction composée :
$$\lim_{\,x\rightarrow -\infty}\left(\sqrt{\dfrac{1}{x^{2}-1}}\right)=0.$$
$\ast$ En $+\infty$ :
On a d'une manière analogue au cas ci-dessus :
$$\lim_{\,x\rightarrow +\infty}\left(\sqrt{\dfrac{1}{x^{2}-1}}\right)=0.$$
8) $f\ :\ x\mapsto\sin\left(\dfrac{\pi x-1}{2x+1}\right)\text{ en }-\infty\;,\ + \infty$
Posons $u(x)=\dfrac{\pi x-1}{2x+1}$ et $v(x)=\sin x.$
On a $\lim_{\,x\rightarrow -\infty}u(x)=\lim_{\,x\rightarrow -\infty}\dfrac{\pi x}{2x}=\dfrac{\pi}{2}$
et $\lim_{\,x\rightarrow\dfrac{\pi}{2}}v(x)=1$, d'où, d'après le théorème sur la limite d'une fonction composée :
$$\lim_{\,x\rightarrow -\infty}\left(\sin\dfrac{\pi x-1}{2x+1}\right)=1.$$
La démarche est tout à fait analogue en $+\infty$ avec le même résultat.
Déterminer une limite par comparaison
Exercice 11
1) $f\ :\ x\mapsto 1+x^{2}\sin\dfrac{1}{x}\text{ en }x_{0}=0$
On a, pour tout $x$ non nul et en particulier pour tout $x$ de $[-1\;;\ 0[\cup]0\;;\ 1]$ :
$-1\leq\sin\dfrac{1}{x}\leq 1$, d'où en multipliant les $3$ membres par $x^{2}\geq 0$, $-x^{2}\leq x^{2}\sin\dfrac{1}{x}\leq x^{2}$, puis en ajoutant $1$ aux $3$ membres de cette dernière inégalité :
$$1-x^{2}\leq 1+x^{2}\sin\dfrac{1}{x}\leq 1+x^{2}.$$
Puisque $\lim_{\,x\rightarrow 0}(1-x^{2})=\lim_{\,x\rightarrow 0}(1+x^{2})=1$, le théorème dit “ des gendarmes ” (ou théorème d'encadrement) permet de conclure que $\lim_{\,x\rightarrow 0}\left(1+x^{2}\sin\dfrac{1}{x}\right)=1.$
2) $f\ :\ x\mapsto\dfrac{\sin x}{x}\text{ en }+\infty\text{ et en }-\infty$
On a pour tout $x$ réel, et en particulier pour tout $x$ de $]-\infty\;;\ 0[$, $-1\leq\sin x\leq 1$, d'où en multipliant les $3$ membres par $\dfrac{1}{x}<0$, $-\dfrac{1}{x}\geq\dfrac{\sin x}{x}\geq\dfrac{1}{x}$ ou encore $\dfrac{1}{x}\leq\dfrac{\sin x}{x}\leq-\dfrac{1}{x}.$
Les relations $\lim_{\,x\rightarrow -\infty}\left(\dfrac{1}{x}\right)=\lim_{\,x\rightarrow -\infty}\left(-\dfrac{1}{x}\right)=0$ et le théorème d'encadrement entraînent alors que :
$$\lim_{\,x\rightarrow -\infty}\left(\dfrac{\sin x}{x}\right)=0$$
De même on a pour tout réel $x$ strictement positif, $-1\leq\sin x\leq 1$, d'où en multipliant les $3$ membres par $\dfrac{1}{x}>0$, $-\dfrac{1}{x}\leq\dfrac{\sin x}{x}\leq\dfrac{1}{x}.$
Les relations $\lim_{\,x\rightarrow +\infty}\left(-\dfrac{1}{x}\right)=0$ et le théorème d'encadrement nous donnent : $$\lim_{\,x\rightarrow +\infty}\left(\dfrac{\sin x}{x}\right)=0$$
3) $f\ :\ x\mapsto\sin\dfrac{1}{x}+\dfrac{1}{x}\text{ en }x_{0}=0$
Pour tout réel $x$ non nul, on a par définition du sinus d'un réel :
$-1\leq\sin\dfrac{1}{x}\leq 1.$
En ajoutant $\dfrac{1}{x}$ aux trois membres de cette dernière inégalité, il vient :
$-1+\dfrac{1}{x}\leq\sin\dfrac{1}{x}+\dfrac{1}{x}\leq 1+\dfrac{1}{x}.$
$\bullet$ Pour $x<0$, l'inégalité $\sin\dfrac{1}{x}+\dfrac{1}{x}\leq 1+\dfrac{1}{x}$ et le fait que $\lim_{\,x\rightarrow 0^{-}}\left(1+\dfrac{1}{x}\right)=-\infty$ entraînent d'après un théorème de comparaison (théorème de majoration) que :
$$\lim_{\,x\rightarrow 0^{-}}\left(\sin\dfrac{1}{x}+\dfrac{1}{x}\right)=-\infty.$$
$\bullet$ Pour $x>0$, l'inégalité $\sin\dfrac{1}{x}+\dfrac{1}{x}\geq 1+\dfrac{1}{x}$ et le fait que $\lim_{\,x\rightarrow 0^{+}}\left(1+\dfrac{1}{x}\right)=+\infty$ entraînent d'après un théorème de comparaison (théorème de minoration) que :
$$\lim_{\,x\rightarrow 0^{+}}\left(\sin\dfrac{1}{x}+\dfrac{1}{x}\right)=+\infty.$$
4) $f\ :\ x\mapsto\dfrac{\sin x+2}{x}\text{ en }+\infty\text{ et en }-\infty$
Pour tout réel $x$, on a par définition du sinus d'un réel : $-1\leq\sin x\leq 1.$
D'où en ajoutant $2$ aux trois membres, $1\leq 2+\sin x\leq 3.$
$\bullet$ Pour tout réel $x$ strictement positif, multiplions les trois membres par $\dfrac{1}{x}>0$ pour obtenir :
$\dfrac{1}{x}\leq\dfrac{2+\sin x}{x}\leq\dfrac{3}{x}.$
Les relations $\lim_{\,x\rightarrow +\infty}\left(\dfrac{1}{x}\right)=\lim_{\,x\rightarrow +\infty}\left(\dfrac{3}{x}\right)=0$ et le théorème d'encadrement nous donnent : $$\lim_{\,x\rightarrow +\infty}\left(\dfrac{2+\sin x}{x}\right)=0$$
$\bullet$ Pour tout réel $x$ strictement négatif, multiplions les trois membres par $\dfrac{1}{x}<0$ pour obtenir :
$\dfrac{1}{x}\leq\dfrac{2+\sin x}{x}\leq\dfrac{3}{x}.$
Les relations $\lim_{\,x\rightarrow -\infty}\left(\dfrac{1}{x}\right)=\lim_{\,x\rightarrow -\infty}\left(\dfrac{3}{x}\right)=0$ et le théorème d'encadrement nous donnent : $$\lim_{\,x\rightarrow -\infty}\left(\dfrac{2+\sin x}{x}\right)=0$$
5) $f\ :\ x\mapsto\cos x-x\text{ en }+\infty\text{ et en }-\infty$
Pour tout réel $x$, on a par définition du cosinus d'un réel : $-1\leq\cos x\leq 1.$
D'où en ajoutant $-x$ aux trois membres, $-1-x\leq\cos x-x\leq 1-x.$
$\bullet$ Pour $x<0$, l'inégalité $\cos x-x\geq -1-x$ et le fait que $\lim_{\,x\rightarrow -\infty}(-1-x)=+\infty$ entraînent d'après un théorème de comparaison (théorème de minoration) que :
$$\lim_{\,x\rightarrow 0^{-}}(\cos x-x)=+\infty.$$
$\bullet$ Pour $x>0$, l'inégalité $\cos x-x\leq 1-x$ et le fait que $\lim_{\,x\rightarrow +\infty}(1-x)=-\infty$ entraînent d'après un théorème de comparaison (théorème de majoration) que : $$\lim_{\,x\rightarrow 0^{-}}(\cos x-x)=-\infty.$$
6) $f\ :\ x\mapsto 1+x^{2}\sin\dfrac{1}{x}\text{ en }0$
Pour tout réel $x$ non nul, on a par définition du sinus d'un réel : $-1\leq \sin\dfrac{1}{x}\leq 1.$
D'où en multipliant les $3$ membres par $x^{2}\geq 0$,
$$-x^{2}\leq x^{2}\sin\dfrac{1}{x}x^{2}.$$
Puis, en ajoutant $1$ aux trois membres, on obtient :
$1-x^{2}\leq 1+x^{2}\sin\dfrac{1}{x}\leq1+x^{2}.$
Les relations $\lim_{\,x\rightarrow 0}(1-x^{2})=\lim_{\,x\rightarrow 0}(1+x^{2})=1$ et le théorème d'encadrement nous donnent : $$\lim_{\,x\rightarrow 0}\left(1+x^{2}\sin\dfrac{1}{x}\right)=1.$$
Étude des branches infinies
Exercice 12
1) Posons $f(x)=\dfrac{x+2}{2x-3}.$
$D_{f}=\left]-\infty\;;\ \dfrac{3}{2}\right[\cup\left]\dfrac{3}{2}\;;\ +\infty\right[.$
$\lim_{\,x\rightarrow -\infty}f(x)=\lim_{\,x\rightarrow -\infty}\left(\dfrac{x}{2x}\right)=\dfrac{1}{2}$ :
il en résulte que la droite $D_{2}$ d'équation $y=\dfrac{1}{2}$ est asymptote à $\mathcal{C}$ au voisinage de $-\infty.$
Le tableau de signes de $2x-3$ autour de $\dfrac{3}{2}$ étant :
$$\begin{array}{|c|lcccr|} \hline x&-\infty& &\dfrac{3}{2}& &+\infty\\ \hline 2x-3& &-&|&+&\\ \hline \end{array}$$
On a :
$\lim_{\,x\rightarrow\left(\dfrac{3}{2}\right)^{-}}f(x)=-\infty$ car $\left\lbrace\begin{array}{lcl} N&\rightarrow&\dfrac{7}{2}\\ D&\rightarrow& 0^{-} \end{array}\right.$
et $\lim_{\,x\rightarrow\left(\dfrac{3}{2}\right)^{+}}f(x)=+\infty$ car $\left\lbrace\begin{array}{lcl} N&\rightarrow&\dfrac{7}{2}\\ D&\rightarrow& 0^{+} \end{array}\right..$
Il en résulte que la droite $\mathcal{D}_{1}$ d'équation $x=\dfrac{1}{2}$ est asymptote verticale à $\mathcal{C}.$
Enfin $\lim_{\,x\rightarrow +\infty}f(x)=\lim_{\,x\rightarrow +\infty}\left(\dfrac{x}{2x}\right)=\dfrac{1}{2}$ :
Il en résulte que la droite $\mathcal{D}_{2}$ d'équation $y=\dfrac{1}{2}$ est asymptote à $\mathcal{C}$ au voisinage de $+\infty.$
Exercice 13
1) $\ast\ lim_{\,x\rightarrow (-2)^{+}}f(x)=\lim_{\,x\rightarrow (-2)^{+}}\left(\sqrt{x+2}\right)=0$ ;
$\ast\ lim_{\,x\rightarrow (-2)^{-}}f(x)=\lim_{\,x\rightarrow (-2)^{-}}\left(\dfrac{2x^{2}-|x^{3}|}{x+2}\right)=\lim_{\,x\rightarrow (-2)^{-}}\left(\dfrac{2x^{2}+x^{3}}{x+2}\right)=\lim_{\,x\rightarrow (-2)^{+}}\left(\dfrac{x^{2}(2+x)}{x+2}\right)$ (car au voisinage de $-2$, $x$ est négatif, donc $x^{3}$ aussi).
D'où $\lim_{\,x\rightarrow (-2)^{-}}f(x)=(-2)^{2}=4.$
Enfin $f(-2)=\sqrt{-2+2}=0.$
Il résulte de ces calculs que $f$ est continue à droite, mais pas à gauche en $-2.$
En résumé, $f$ n'est pas continue en $-2.$
2) On a, pour tout $x$ de $]-\infty\;;\ -2[$, $f(x)=\dfrac{2x^{2}+x^{3}}{x+2}=x^{2}$ (après simplification par $(x+2)$ comme ci-dessus).
Exercice 14
1) $f\ :\ x\mapsto 3x^{2}+x-1$
$f$ est définie et continue sur $\mathbb{R}$ comme fonction polynôme.
2) $f\ :\ x\mapsto\dfrac{2x+1}{2x-1}$
$f$ est définie et continue sur $\mathbb{R}\setminus\left\lbrace\dfrac{1}{2}\right\rbrace$ comme fonction rationnelle.
3) $f\ :\ x\mapsto\sqrt{x^{2}+5x-5}$
$f(x)$ existe si et seulement si $x^{2}+5x-5\geq 0$, soit après calcul des racines du trinôme, $x\in D=\left]-\infty\;;\ \dfrac{-5+3\sqrt{5}}{2}\right]\cup\left[\dfrac{-5+3\sqrt{5}}{2}\;;\ +\infty\right[.$
La fonction $g\ :\ x\mapsto x^{2}+5x-5$ étant continue et positive sur $D$, il résulte d'un théorème du cours de Première que la fonction $f=\sqrt{g}$ est continue sur $D.$
Auteur:
Mouhamadou ka

Commentaires
AMANI (non vérifié)
ven, 10/01/2021 - 13:01
Permalien
DEMANDE INTEGRATION
AMANI (non vérifié)
ven, 10/01/2021 - 13:01
Permalien
DEMANDE INTEGRATION
Anonyme (non vérifié)
ven, 07/19/2024 - 02:51
Permalien
Bien
Serigne fallou sarr (non vérifié)
lun, 11/11/2024 - 23:48
Permalien
Bac
Ajouter un commentaire