Vous êtes ici

Solution des exercices : Énergie cinétique - 1er s

Classe:

Première

Exercice 1

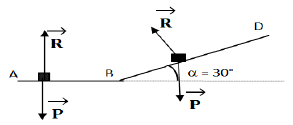
1. Exprimons, puis calculons l'énergie cinétique de l'autoporteur en

$A.$

$\begin{array}{rcl} E_{C_{A}} &=&\dfrac{1}{2}mV_{A}^{2}\\ &=&\dfrac{1}{2}\times 600\cdot 10^{-3}\times 6^{2} \\\Rightarrow E_{C_{A}} &=&10.8J \end{array}$

2. Inventaire des forces extérieures agissant sur l'autoporteur au cours de la phase

$AB.$

Les forces extérieures sont :

$\overrightarrow{P}$ et

$\overrightarrow{R}$

3. a) Définition d'un système pseudo-isolé ;

Un système pseudo-isolé est un système soumis à des forces qui se compensent.

b) L'autoporteur est pseudo-isolé au cours de la phase

$AB$ , car, pendant cette phase les forces se compensent.

Par contre, pendant la phase

$BD$ , les forces ne se compensent plus, et le système n'est plus pseudo-isolé

c) Déduction de la vitesse du centre d'inertie du mobile en

$B$

Le théorème de l'énergie cinétique s'écrit :

$\begin{array}{rcl} \Delta BC &=& \sum\,W\left(\overrightarrow{F}_{extérieurs}\right)\\\Rightarrow\;E_{CB}-E_{CA}&=&W_{AB}\left(\overrightarrow{P}\right)+W_{AB}\left(\overrightarrow{R}\right) \\\Rightarrow\dfrac{1}{2}mV_{B}^{2}-\dfrac{1}{2}mV_{A}^{2}&=&0+0\\\Rightarrow\dfrac{1}{2}mV_{A}^{2}&=&\dfrac{1}{2}mV_{B}^{2}\\\Rightarrow\;V_{B}^{2}&=&V_{A}^{2}\\\Rightarrow\;V_{B}&=&V_{A}\\ \Rightarrow\;V_{B}&=&6m\cdot s^{-1} \end{array}$

4. Calcul du travail du poids de l'autoporteur et le travail de l'action

$R$ du plan sur l'autoporteur au cours du déplacement

$BC_{1}$

$\begin{array}{rcl} W_{BC_{1}}\left(\overrightarrow{P}\right) &=&\overrightarrow{P}\cdot\overrightarrow{BC_{1}}\\ &=&-mgBC_{1}\sin\alpha\nonumber\\ &=&-600\cdot 10^{-3}\times 10\times 1\times\sin 30^{\circ} \\ \Rightarrow\;W_{BC_{1}}\left(\overrightarrow{P}\right) &=&-3.0J \end{array}$

$W_{BC_{1}}\left(\overrightarrow{R}\right)=\overrightarrow{R}\cdot\overrightarrow{BC_{1}}=0\left(\overrightarrow{R}\perp\overrightarrow{BC_{1}}\right)$

5. Déduction de

$V_{c_{1}}$

Le théorème de l'énergie cinétique au solide entre les instants

$t_{B}$ et

$t_{C_{1}}$ s'écrit :

$\begin{array}{rcl} E_{C_{c_{1}}}-E_{C_{B}}&=&W_{BC_{1}}\left(\overrightarrow{P}\right)+W_{BC_{1}}\left(\overrightarrow{R}\right)\\\Rightarrow\dfrac{1}{2}mV_{C_{1}}^{2}-\dfrac{1}{2}mV_{B}^{2}&=&-mgBC_{1}\sin\alpha+0\\\Rightarrow\;V_{C_{1}}^{2}-V_{B}^{2}&=&-2gBC_{1}\sin\alpha\\\Rightarrow\; V_{C_{1}}^{2}&=&V_{B}^{2}-2gBC_{1}\sin\alpha\\\Rightarrow\; V_{C_{1}} &=&\sqrt{V_{B_{1}}-2gBC_{1}\sin\alpha}\\ \Rightarrow\; V_{C_{1}}&=&\sqrt{6^{2}-2\times 10\times 1\times\sin 30^{\circ}}\\\Rightarrow\;V_{C_{1}} &=&5.1\,m\cdot s^{-1} \end{array}$

6. Déduction de

$BC_{2}$ la distance parcourue par le mobile avant de rebrousser chemin en

$C_{2}.$

$\begin{array}{rcl} E_{C_{c_{1}}}-E_{C_{B}} &=& W_{BC_{2}}\left(\overrightarrow{P}\right)+W_{BC_{2}}\left(\overrightarrow{R}\right)\\\Rightarrow\;0-\dfrac{1}{2}mV_{B}^{2} &=&-mgBC_{2}\sin\alpha+0 \\\Rightarrow \;-V_{B}^{2} &=& -2gBC_{2}\sin\alpha\\\Rightarrow\; 2gBC_{2}\sin\alpha &=&V_{B}^{2} \\\Rightarrow\; BC_{2} &=&\dfrac{V_{B}^{2}}{2g\sin\alpha}\\\Rightarrow\;BC_{2} &=&\dfrac{6^{2}}{2\times 10\sin 30^{\circ}}\\\Rightarrow \;BC_{2} &=&3.6\,m \end{array}$

Exercice 2

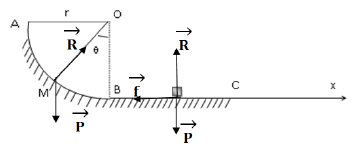
1.1. Bilan des forces qui s'appliquant sur le mobile au point

$M$ sont :

$\overrightarrow{P}$ et

$\overrightarrow{R}.$

1.2. Expression du travail de chacune des forces, au point

$M$ , en fonction de

$m$ ,

$g$ ,

$r$ et

$\theta.$

$W_{AM}\left(\overrightarrow{P}\right)=\overrightarrow{P}\cdot\overrightarrow{AM}=mgr\cos\theta$

$W_{AM}\left(\overrightarrow{R}\right)=\overrightarrow{R}\cdot\overrightarrow{AB}=0\quad\text{car}\quad\overrightarrow{R}\perp\overrightarrow{AB}$

1.3. Établissement de l'expression littérale de la vitesse

$V_{M}$ du mobile en fonction de

$V_{A}$ ,

$g$ ,

$r$ et

$\theta.$

Appliquons le théorème de l'énergie cinétique au point

$M$ et

$\begin{array}{rcl} E_{C_{M}}-E_{C_{A}} &=& W_{AM}\left(\overrightarrow{P}\right)+W_{AM}\left(\overrightarrow{R}\right)\\\Rightarrow\dfrac{1}{2}mV_{M}^{2} &=&mgr\cos\theta+0\\\Rightarrow\dfrac{1}{2}mV_{M}^{2} &=&\dfrac{1}{2}mV_{A}^{2}+mgr\cos\theta\\\Rightarrow \;V_{M}^{2} &=&V_{A}^{2}+2gr\cos\theta\\\Rightarrow\; V_{M} &=&\sqrt{V_{A}^{2}+2gr\cos\theta} \end{array}$

1.4. Calcul de

$V_{M}$ en

$B$

$($ pour

$\theta=0).$

$\begin{array}{rcl} V_{M} &=&\sqrt{V_{A}^{2}+2gr\cos\theta}\ ;\ \text{pour }\theta=0\\\Rightarrow\; V_{M} &=& \sqrt{V_{A}^{2}+2gr\cos 0}\\\Rightarrow \;V_{B} &=&\sqrt{V_{A}^{2}+2gr}\\\Rightarrow \;V_{B} &=&\sqrt{5^{2}+2\times 10\times 1}\\\Rightarrow \;V_{B} &=&6.71\,m\cdot s^{-1} \end{array}$

2. Détermination de l'expression littérale et numérique de

$f.$

$\begin{array}{rcl} E_{C_{C}}-E_{C_{B}} &=& W_{BC}\left(\overrightarrow{P}\right)+W_{BC}\left(\overrightarrow{R}\right)+W_{BC}\left(\overrightarrow{f}\right)\\\Rightarrow\dfrac{1}{2}mV_{C}^{2}-\dfrac{1}{2}mV_{B}^{2} &=&0+0-f\times BC\\\Rightarrow \;f &=&\dfrac{m\left(V_{B}^{2}\right)}{2BC}\\\Rightarrow\; f &=&\dfrac{0.1\times\left(6.71^{2}-5\right)}{2\times 1} \\\Rightarrow \;f &=& 1N \end{array}$

Exercice 3 Voiture tremplin

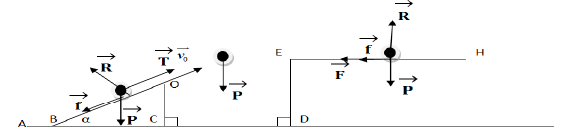
1. Dans le référentiel terrestre supposé galiléen, les forces s'exerçant sur le système {ensemble automobile-pilote} sont :

$-\$ dans la phase

$BO$ : son poids

$\overrightarrow{P}$ , la réaction

$\overrightarrow{R}$ du support, les frottements

$\overrightarrow{f}$ et la traction

$\overrightarrow{T}$ du système.

$-\$ dans la phase

$OE$ : son poids

$\overrightarrow{P}.$

$-\$ dans la phase

$EH$ : son poids

$\overrightarrow{P}$ , la réaction normale

$\overrightarrow{R}$ du support, les frottements

$\overrightarrow{f}$ et la force de freinage

$\overrightarrow{F}$

2. Si on suppose que le système est soumis à des forces qui ne se compensent pas dans la phase

$BO$ , alors le système n'est pas pseudo isolé (d'après le principe d'inertie).

Si on suppose qu'il évolue à vitesse constante et à trajectoire rectiligne, alors le système est pseudo isolé (d'après le principe d'inertie).

Dans la phase

$OE$ , le système n'est soumis qu'à son poids ; il n'est donc pas pseudo isolé.

Dans la phase

$EH$ , le système freine donc(les forces ne se compensent plus), d'après le principe d'inertie, il n'est pas pseudo isolé.

3. Détermination du travail de chaque force de chacune des phases :

$-\$ Phase

$BO$

$\begin{array}{rcl} W_{BO}\left(\overrightarrow{P}\right) &=&-mg\cdot OC\\ &=&-1.00\cdot 10^{3}\times 9.81\times 8.00\\ &=&-78.5\cdot 10^{3}J \end{array}$

$W_{BO}\left(\overrightarrow{R}\right)=0\quad\text{car}\quad\overrightarrow{R}\perp\overrightarrow{BO}$

$\begin{array}{rcl} W_{BO}\left(\overrightarrow{f}\right) &=&\overrightarrow{f}\cdot BO\\ &=&-\dfrac{500\times 8.00}{\sin 15.5^{\circ}}\\\Rightarrow W_{BO}\left(\overrightarrow{f}\right) &=&-15.5\cdot 10^{3}J \end{array}$

$\begin{array}{rcl} W_{BO}\left(\overrightarrow{T}\right) &=& \overrightarrow{T}\cdot\overrightarrow{BO}\\ &=&\dfrac{T\times OC}{\sin\alpha} \end{array}$

$-\$ Phase

$OE$

$\begin{array}{rcl} W_{BO}\left(\overrightarrow{P}\right) &=&-mg(ED-OC)\\ &=&-1.00\cdot 10^{3}\times 9.81\times(10.0-8.00)\\ &=&-19.6\cdot 10^{3}J\end{array}$

$-\$ Phase

$EH$

$W_{EH}\left(\overrightarrow{P}\right)=0J\ (\overrightarrow{P}\perp\overrightarrow{BH})$

$W_{EH}\left(\overrightarrow{f}\right)=0J\ (\overrightarrow{R}\perp\overrightarrow{EH})$

$\begin{array}{rcl} W_{EH}\left(\overrightarrow{f}\right) &=&-500\times 100\\\Rightarrow\; W_{EH}\left(\overrightarrow{f}\right)&=&-50.0\cdot 10^{3}J \end{array}$

4. D'après le théorème de l'énergie cinétique (dans un référentiel galiléen, la variation d'énergie cinétique d'un système en translation entre deux points est égale à la somme des travaux des forces qui s'exercent sur ce système entre ces deux points.) entre

$O$ et

$E$ , on a :

$\dfrac{1}{2}mv_{1}^{2}-\dfrac{1}{2}mv_{0}^{2} =W_{OE}\left(\overrightarrow{P}\right)$

$\begin{array}{rcl} \text{ soit }\ \dfrac{1}{2}mv_{1}^{2}-\dfrac{1}{2}mv_{0}^{2} &=&mg(OC-ED)\\\Rightarrow\; v_{0} &=&\sqrt{v_{1}^{2}+2g(DE-OC)}\\\Rightarrow\; v_{0} &=&\sqrt{24^{2}+2\times 9.81(10.0-8.00)}\\\Rightarrow \;v_{0} &=&24.8\,m\cdot s^{-1} \end{array}$

5. D'après le théorème de l'énergie cinétique entre

$E$ et

$H$ , on a :

$\dfrac{1}{2}mv_{H}^{2}-\dfrac{1}{2}mv_{1}^{2} =W_{EH}\left(\overrightarrow{F}\right)+W_{EH}\left(\overrightarrow{f}\right).$

$v_{H}=0\,m\cdot s^{-1}$

d'où il vient :

$-\dfrac{1}{2}mv_{1}^{2}=-f\times EH-F\times EH.$

Donc

$F=\dfrac{mv_{1}^{2}}{2EH}-f=\dfrac{1.00\cdot 10^{3}\times 24^{2}}{2\times 10.00}-500=23.8\cdot 10^{3}.$

6. La puissance du travail de la force

$\overrightarrow{F}$

$\begin{array}{rcl} P &=&\dfrac{W_{EH}\left(\overrightarrow{F}\right)}{t}\\ &=&\dfrac{-F\times EH}{t}\\ &=&\dfrac{-23.8\cdot 10^{3}\times 10.00}{8.00}\\ &=& -29.8\cdot 10^{3}W. \end{array}$

Exercice 4

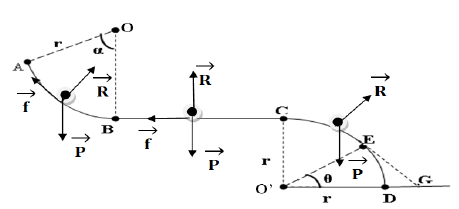
1. Calcul des vitesses

$V_{B}$ et

$V_{C}$ avec lesquelles le skieur passe en

$B$ et en

$C.$

$\bullet\$ Système étudié : le skieur

$\bullet\$ Référentiel d'étude : référentiel terrestre supposé galiléen

$\bullet\$ Bilan des forces appliquées :

$\overrightarrow{P}$ et

$\overrightarrow{R}$

Le théorème de l'énergie cinétique s'écrit :

$-\$ entre

$A$ et

$B$

$\begin{array}{rcl} E_{c_{B}}-E_{c_{A}}&=&W_{AB}\left(\overrightarrow{P}\right)+W_{AB}\left(\overrightarrow{R}\right)\\\Rightarrow\dfrac{1}{2}mV_{B^{2}}-0&=&mgr(1-\cos\alpha)+0\\\Rightarrow\dfrac{1}{2}mV_{B^{2}}&=&mgr(1-\cos\alpha)\\ \Rightarrow\;V_{B^{2}}&=&2gr(1-\cos\alpha)\\\Rightarrow\;V_{B}&=&\sqrt{2gr(1-\cos\alpha)}\\&=&\sqrt{2\times 10\times 5\left(1-\cos 60^{\circ}\right)}\\\Rightarrow\;V_{B}&=&7.07m\cdot s^{-1} \end{array}$

$-\$ entre

$B$ et

$C$

$\begin{array}{rcl} E_{c_{C}}-E_{c_{B}}&=&W_{BC}\left(\overrightarrow{P}\right)+W_{BC}\left(\overrightarrow{R}\right)\\\Rightarrow\dfrac{1}{2}mV_{C}^{2}-\dfrac{1}{2}mV_{B}^{2}&=&0+0\\\Rightarrow\;V_{C}^{2}&=&V_{B}^{2}\\\Rightarrow\;V_{C}&=&V_{B}\\\Rightarrow\;V_{C}&=&7.07m\cdot s^{-1} \end{array}$

2.1 Expression de

$V_{B}$ en fonction de

$m$ ,

$r$ ,

$f$ , et

$g.$

Le théorème de l'énergie cinétique s'écrit :

$-\$ entre

$A$ et

$B$

$\begin{array}{rcl} E_{c_{B}}-E_{c_{A}}&=&W_{AB}\left(\overrightarrow{P}\right)+W_{AB}\left(\overrightarrow{R}\right)+W_{AB}\left(\overrightarrow{f}\right)\\\Rightarrow\dfrac{1}{2}mV_{B}^{2}-0&=&mgr(1-\cos\alpha)+0-fr\alpha\text{ avec }\left(\alpha=\dfrac{\pi}{3}\right)\\ \Rightarrow\dfrac{1}{2}mV_{B}^{2}&=&mgr(1-\cos\alpha)-f\times\dfrac{\pi}{3}r\\ \Rightarrow\;V_{B}^{2}&=&2gr(1-\cos\alpha)-2f\times\dfrac{\pi}{3}r\\ \Rightarrow\;V_{B}&=&\sqrt{2gr\left(1-\cos\alpha\right)-2f\times\dfrac{\pi}{3}r} \end{array}$

2.2 Expression de

$V_{c}$ en fonction de

$m$ ,

$r$ ,

$f$ et

$V_{B}$

Le théorème de l'énergie cinétique s'écrit :

$-\$ entre

$B$ et

$C$

$\begin{array}{rcl} E_{c_{C}}-E_{c_{B}}&=&W_{BC}\left(\overrightarrow{P}\right)+W_{BC}\left(\overrightarrow{R}\right)+W_{BC}\left(\overrightarrow{f}\right)\\ \Rightarrow\dfrac{1}{2}mV_{C}^{2}-\dfrac{1}{2}mV_{B}^{2}&=&0+0-fr\\ \Rightarrow\;V_{C}^{2}&=&2V_{B}^{2}-\dfrac{2fr}{m}\\\Rightarrow\;V_{C}&=&\sqrt{2\left(V_{B}^{2}-\dfrac{fr}{m}\right)} \end{array}$

2.3 Calcul de l'intensité de la force de frottement

$\begin{array}{rcl} V_{c}&=&\sqrt{2\left(V_{B}^{2}-\dfrac{fr}{m}\right)}\\&=&0\\ \Rightarrow\;2\left(V_{B}^{2}-\dfrac{fr}{m}\right)&=&0\\ \Rightarrow\dfrac{fr}{m}&=&V_{B}^{2}\\\Rightarrow\;f&=&\dfrac{mV_{B}^{2}}{r}\\&=&\dfrac{80\times 7.07^{2}}{5}\\\Rightarrow\;f&=&8.0\cdot 10^{2}N \end{array}$

3.1 Expression de la vitesse

$V_{E}$ en fonction de

$g$ ,

$r$ et

$\theta$

Le théorème de l'énergie cinétique s'écrit :

$-\$ entre

$C$ et

$E$

$\begin{array}{rcl} E_{c_{E}}-E_{c_{C}}&=&W_{CE}\left(\overrightarrow{P}\right)+W_{CE}\left(\overrightarrow{R}\right)\\\Rightarrow\dfrac{1}{2}mV_{E}^{2}-0&=&mgr(1-\sin\theta)\\\Rightarrow\;V_{E}^{2}&=&2gr(1-\sin\theta)\\\Rightarrow\;V_{E}&=&\sqrt{2gr(1-\sin\theta)} \end{array}$

3.2 Calcul de la valeur de l'angle

$\theta$

$\begin{array}{rcl} V_{E}^{2}&=&2gr(1-\sin\theta)\\\Rightarrow(1-\sin\theta)&=&\dfrac{V_{E}^{2}}{2gr}\\ \Rightarrow\sin\theta&=&1-\dfrac{V_{E}^{2}}{2gr}\\\Rightarrow\theta&=&\sin^{-1}\left(1-\dfrac{V_{E}^{2}}{2gr}\right)\\\Rightarrow\theta&=&\sin^{-1}\left(1-\dfrac{5.77^{2}}{2\times 10\times 5}\right)\\ \Rightarrow\theta&=& 60^{\circ} \end{array}$

4. vitesse avec laquelle le skireur atterrit sur la piste de réception en un point

$G$

$\begin{array}{rcl} V_{E}&=&\sqrt{2gr(1-\sin\theta)}\;,\text{ au point }G\;,\ \theta=0\\\Rightarrow\;V_{E}&=&\sqrt{2gr(1-\sin 0)}\\\Rightarrow\;V_{E}&=&\sqrt{2gr}\\&=&\sqrt{2\times10\times5}\\\Rightarrow\;V_{E}&=&10\,m\cdot s^{-1} \end{array}$

Commentaires

Ilyass elbari (non vérifié)

mer, 01/06/2021 - 22:01

Vous êtes ici

Solution des exercices : Énergie cinétique - 1er s

Formulaire de recherche

Exercice 1

Exercice 2

Exercice 3 Voiture tremplin

Exercice 4

Commentaires

Pages

Ajouter un commentaire

Plain text