Corrigé BFEM maths 2013
Exercice 1
Une enquête portant sur le nombre de filles fréquentant une classe de terminales scientifiques, menée dans les $50$ établissements scolaires d'une localité, a donné le relevé ci-dessous :
$$\begin{array}{ccccccccccccccc} 12&11&10&14&8&0&5&10&7&10&14&10&13&14&4\\18&10&10&7&10&4&10&13&11&13&18&4&13&12&18\\17&0&6&5&5&6&10&10&9&7&11&4&15&17&16\\16&15&10&0&8&&&&&&&&&&\end{array}$$
1) a) Les établissements scolaires d'une localité constituent la population étudiée.
b) Le nombre de filles fréquentant une classe de terminales scientifiques est le caractère étudié.
Ce caractère étant mesurable donc, il est de nature quantitative.
c) $18$ est une modalité de ce caractère d'effectif partiel $3$ ; c'est à dire, on trouve $3$ établissements dans lesquels $18$ filles fréquentent une classe de terminales scientifiques.
2) a) Calculons l'effectif moyen $M$ de filles en terminales scientifiques dans ces établissements.
On a :
$$M=\dfrac{\text{nombre total de filles fréquentant une classe de terminales scientifiques}}{\text{nombre total d'établissements}}$$
Ainsi, $M=\dfrac{500}{50}=10$
D'où, l'effectif moyen $M$ de filles en terminales scientifiques dans ces établissements est égal à $10.$
b) Déterminons la médiane $m$ de cette série statistique.
L'effectif total étant $N=50$ alors, sa moitié est égale à $\dfrac{50}{2}=25.$
Donc, la médiane $m$ sera donnée par :
$$m=\dfrac{\text{effectif du 25e établissement}+\text{effectif du 26e établissement}}{2}$$
Déterminons alors, les effectifs du $25e$ et du $26e$ établissement dans l'ordre du décompte.
En rangeant le relevé de données dans l'ordre croissant, on obtient :
$$\begin{array}{ccccccccccccccc} 0&0&0&4&4&4&4&5&5&5&6&6&7&7&7\\8&8&9&10&10&10&10&10&10&10&10&10&10&10&11\\11&11&12&12&13&13&13&13&14&14&14&15&15&16&16\\17&17&18&18&18&&&&&&&&&&\end{array}$$
Ainsi, on constate que le $25e$ et le $26e$ établissement comptent chacun $10$ filles en terminales scientifiques.
Par suite, $m=\dfrac{10+10}{2}=\dfrac{20}{2}=10$
c) Déterminons le nombre d'établissements scolaires où on a au moins $10$ filles en classes de terminales scientifiques.
Cela revient à dénombrer les établissements qui comptent un nombre supérieur ou égal à $10$ filles en classes de terminales scientifiques.
En faisant le décompte, on trouve $32$
3) a) Regroupons les données recueillies en classes d'amplitude $5.$
$$\begin{array}{|c|c|c|c|c|}\hline\text{Classes}&[0\;;\ 5[&[5\;;\ 10[&[10\;;\ 15[&[15\;;\ 20[\\\hline\text{Effectif partiel}&7&11&23&9\\\hline\end{array}$$
b) Dressons le tableau statistique de la série comprenant l'effectif et l'effectif cumulé décroissant de chacune des classes.
$$\begin{array}{|l|c|c|c|c|}\hline\text{Classes}&[0\;\ 5[&[5\;;\ 10[&[10\;;\ 15[&[15\;,\ 20[\\\hline\text{Effectif partiel}&7&11&23&9\\\hline\text{E.C.D}&50&43&32&9\\\hline\end{array}$$
4) Construisons l'histogramme des effectifs cumulés décroissants et le diagramme des effectifs cumulés décroissants de cette série.
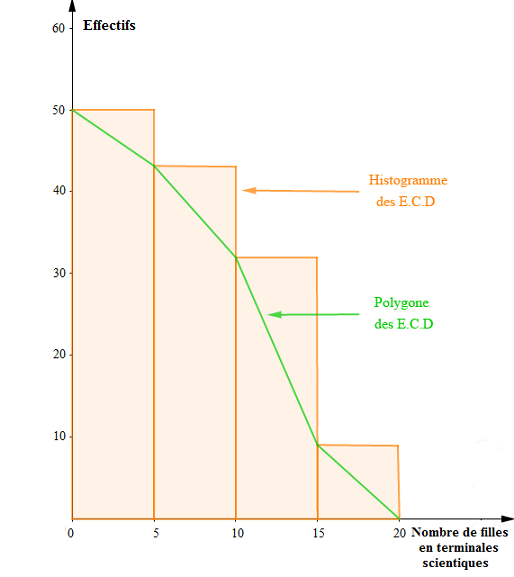
$$\begin{array}{rcl}\text{Échelle}\ :\ 2\;cm&\longrightarrow&5\text{ filles}\\1\;cm&\longrightarrow&5\text{ établissements}\end{array}$$
Exercice 2
On pose $f(x)=|-x+2|$
1) Exprimons $f(x)$ sans le symbole de la valeur absolue.
Soit :
$$\left\lbrace\begin{array}{rcccl} |-x+2|&=&-x+2&\text{si}&-x+2\geq 0\\ \\|-x+2|&=&-(-x+2)&\text{si}&-x+2\leq 0\end{array}\right.$$
Or, on a :
$\begin{array}{rcrcl} -x+2\geq 0&\Leftrightarrow&-x&\geq&-2\\ \\&\Leftrightarrow&x&\leq&2\end{array}$
De même,
$\begin{array}{rcrcl} -x+2\leq 0&\Leftrightarrow&-x&\leq&-2\\ \\&\Leftrightarrow&x&\geq&2\end{array}$
Donc,
si $x\leq 2$ alors, $|-x+2|=-x+2$
si $x\geq 2$ alors, $|-x+2|=-(-x+2)=x-2$
D'où,
$$\left\lbrace\begin{array}{rcccl} f(x)&=&-x+2&\text{si}&x\leq 2\\ \\f(x)&=&x-2&\text{si}&x\geq 2\end{array}\right.$$
2) Calculons $f(0)\ $ et $\ f(2).$
Comme $0<2$ alors, pour calculer $f(0)$ on utilise l'expression $f(x)=-x+2.$
Donc, $f(0)=0+2=2$
Ainsi, $\boxed{f(0)=2}$
Pour calculer $f(2)$, on utilise une des deux expressions de $f(x)$, par exemple en choisissant $f(x)=x-2.$, on obtient :
$f(2)=2-2=0$
De même en choisissant $f(x)=-x+2$, on trouve :
$f(2)=-2+2=0$
D'où, finalement $\boxed{f(2)=0}$
3) Résolvons dans $\mathbb{R}$ l'équation $|-x+2|=|4x+5|.$
On sait que : $|-x+2|=|4x+5|$ si, et seulement si,
$$-x+2=4x+5\quad\text{oubien}\quad -x+2=-(4x+5)$$
On obtient alors deux équations que nous allons résoudre séparément.
$-\ $ Équation (1) : $-x+2=4x+5$
$\begin{array}{rcrclcrcl} -x+2=4x+5&\Leftrightarrow&-x-4x&=&5-2\\ \\&\Leftrightarrow&-5x&=&3\\ \\&\Leftrightarrow&x&=&\dfrac{3}{-5}\end{array}$
$-\ $ Équation (2) : $-x+2=-(4x+5)$
$\begin{array}{rcrclcrcl} -x+2=-(4x+5)&\Leftrightarrow&-x+2&=&-4x-5\\ \\&\Leftrightarrow&-x+4x&=&-5-2\\ \\&\Leftrightarrow&3x&=&-7\\ \\&\Leftrightarrow&x&=&\dfrac{-7}{3}\end{array}$
D'où, l'ensemble des solutions sera donné par :
$$S=\left\lbrace -\dfrac{7}{3}\;;\ -\dfrac{3}{5}\right\rbrace$$
Exercice 3
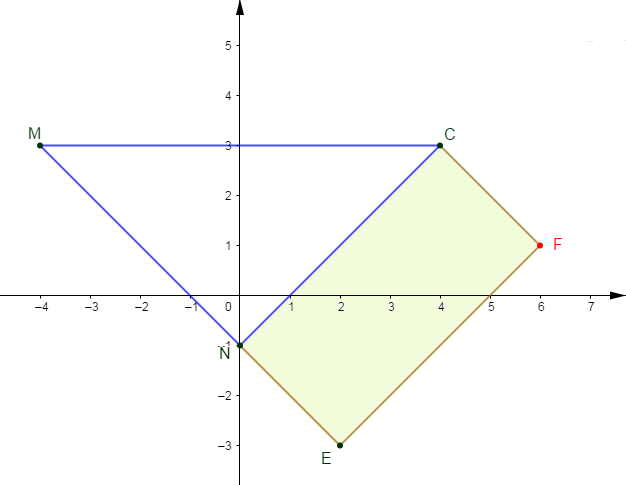
1) Le plan est muni d'un repère orthonormal $(O\;,\ I\;,\ J)$ tel que $OI=OJ=1\;cm.$
Plaçons les points $M (-4\;;\ 3)\;,\ N (0\;;\ -1)\;,\ C(4\;;\ 3)\ $ et $\ E(2\;;\ -3).$

2) Montrons que les points $M\;,\ N\ $ et $\ E$ sont alignés.
Pour cela, il suffit de montrer que les vecteurs $\overrightarrow{MN}\ $ et $\ \overrightarrow{NE}$ sont colinéaires.
Soit : $\overrightarrow{MN}\begin{pmatrix} 0-(-4)\\-1-3\end{pmatrix}=\begin{pmatrix} 4\\-4\end{pmatrix}\ $ et $\ \overrightarrow{NE}\begin{pmatrix} 2-0\\-3-(-1)\end{pmatrix}=\begin{pmatrix} 2\\-2\end{pmatrix}$
On a :
$\begin{array}{rcl} x_{\overrightarrow{MN}}\times y_{\overrightarrow{NE}}-x_{\overrightarrow{NE}}\times y_{\overrightarrow{MN}}&=&4\times(-2)-2\times(-4)\\ \\&=&-8+8\\ \\&=&0\end{array}$
Donc, les coordonnées des vecteurs $\overrightarrow{MN}\ $ et $\ \overrightarrow{NE}$ vérifient la propriété :
$$x_{\overrightarrow{MN}}\times y_{\overrightarrow{NE}}-x_{\overrightarrow{NE}}\times y_{\overrightarrow{MN}}=0$$
Par suite, les vecteurs $\overrightarrow{MN}\ $ et $\ \overrightarrow{NE}$ sont colinéaires.
D'où, les points $M\;,\ N\ $ et $\ E$ sont alignés.
3) Calculons $MN$, $NC\ $ et $\ MC$
$-\ $ Calcul de $MN$
On a :
$\begin{array}{rcl} MN&=&\sqrt{(4)^{2}+(-4)^{2}}\\ \\&=&\sqrt{16+16}\\ \\&=&\sqrt{32}\\ \\&=&4\sqrt{2}\end{array}$
Ainsi, $\boxed{MN=4\sqrt{2}\;cm}$
$-\ $ Calcul de $NC$
Soit : $\overrightarrow{NC}\begin{pmatrix} 4-0\\3-(-1)\end{pmatrix}=\begin{pmatrix} 4\\4\end{pmatrix}$ donc,
$\begin{array}{rcl} NC&=&\sqrt{(4)^{2}+(4)^{2}}\\ \\&=&\sqrt{16+16}\\ \\&=&\sqrt{32}\\ \\&=&4\sqrt{2}\end{array}$
D'où, $\boxed{NC=4\sqrt{2}\;cm}$
$-\ $ Calcul de $MC$
Soit : $\overrightarrow{NC}\begin{pmatrix} 4-(-4)\\3-3\end{pmatrix}=\begin{pmatrix} 8\\0\end{pmatrix}$ alors,
$\begin{array}{rcl} MC&=&\sqrt{(8)^{2}+(0)^{2}}\\ \\&=&\sqrt{(8)^{2}}\\ \\&=&|8|\\ \\&=&8\end{array}$
Ainsi, $\boxed{MC=8\;cm}$
Déduisons-en que le triangle $MNC$ est rectangle et isocèle.
Tout d'abord, on remarque que $MN=NC$, ce qui signifie que le triangle $MNC$ est isocèle en $N.$
De plus,
$\begin{array}{rcl} MN^{2}+NC^{2}&=&(4\sqrt{2})^{2}+(4\sqrt{2})^{2}\\ \\&=&4^{2}\times 2+4^{2}\times 2\\ \\&=&32+32\\ \\&=&64\end{array}$
Or, $MC^{2}=8^{2}=64$ donc, $MN^{2}+NC^{2}=MC^{2}$
D'où, d'après la réciproque du théorème de Pythagore, le triangle $MNC$ est rectangle en $N.$
Par conséquent, le triangle $MNC$ est rectangle et isocèle en $N.$
4) a) Calculons les coordonnées du point $F$ tel que le quadrilatère $CNEF$ soit un rectangle.
Pour cela, déterminons d'abord les coordonnées $F$ pour que $CNEF$ soit un parallélogramme.
$CNEF$ un parallélogramme alors, $\overrightarrow{EF}=\overrightarrow{NC}$
Or, $\overrightarrow{EF}\begin{pmatrix} x_{F}-2\\y_{F}-(-3)\end{pmatrix}=\begin{pmatrix} x_{F}-2\\y_{F}+3\end{pmatrix}\ $ et $\ \overrightarrow{NC}\begin{pmatrix} 4\\4\end{pmatrix}$
Donc,
$\begin{array}{rcl}\overrightarrow{EF}=\overrightarrow{NC}&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{F}-2&=&4\\ \\y_{F}+3&=&4\end{array}\right.\\ \\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{F}&=&4+2\\ \\y_{F}&=&4-3\end{array}\right.\\ \\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{F}&=&6\\ \\y_{F}&=&1\end{array}\right.\end{array}$
Ainsi, $x_{F}=6\ $ et $\ y_{F}=1$
D'où,
$$F\begin{pmatrix} 6\\1\end{pmatrix}$$
Par ailleurs, $MNC$ triangle rectangle isocèle en $N$ donc, $\overrightarrow{CN}\ $ et $\ \overrightarrow{MN}$ sont orthogonaux.
Or, les $M\;,\ N\ $ et $\ E$ sont alignés donc, $\overrightarrow{CN}\ $ et $\ \overrightarrow{NE}$ sont orthogonaux.
De plus,
$\begin{array}{rcl} NE&=&\sqrt{(2)^{2}+(-2)^{2}}\\ \\&=&\sqrt{4+4}\\ \\&=&\sqrt{8}\\ \\&=&2\sqrt{2}\end{array}$
Par suite, $NE<NC$
D'où, le quadrilatère $CNEF$ est un rectangle.
b) Calculons l'aire de ce rectangle.
Soit :
$\begin{array}{rcl} \mathcal{A}_{_{CNEF}}&=&NC\times NE\\ \\&=&(4\sqrt{2})\times(2\sqrt{2})\\ \\&=&4\times 2\times 2\\ \\&=&16\end{array}$
Ainsi, $\boxed{\mathcal{A}_{_{CNEF}}=16\;cm^{2}}$
Exercice 4
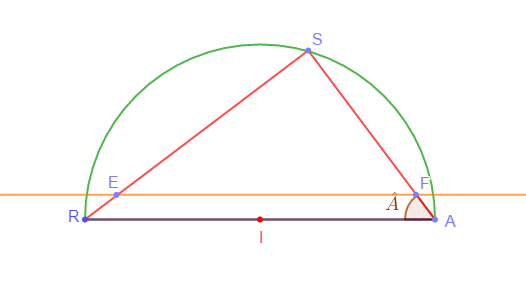
1) Traçons un demi-cercle de centre $I$ et de diamètre $[RA]$ tel que $RA=7\;cm.$

2) Traçons la corde $[RS]$ telle que $RS=5.6\;cm.$
voir figure
3) Démontrons que le triangle $RAS$ est rectangle en $S.$
$[RA]\;,\ [RS]\ $ et $\ [AS]$ sont trois cordes du demi-cercle de centre $I$
Comme l'une des cordes $[RA]$ est diamètre de ce demi-cercle alors, le triangle $RAS$ est rectangle en $S.$
4) Calculons $AS\ $ et $\ \tan\hat{A}.$
$-\ $ Calcul de $AS$
Le triangle $RAS$ étant rectangle en $S$, alors en appliquant le théorème de Pythagore, on a :
$$RA^{2}=AS^{2}+RS^{2}$$
Par suite,
$\begin{array}{rcrcl} AS^{2}=RA^{2}-RS^{2}&\Rightarrow&AS&=&\sqrt{RA^{2}-RS^{2}}\\ \\&\Rightarrow&AS&=&\sqrt{(7)^{2}-(5.6)^{2}}\\ \\&\Rightarrow&AS&=&\sqrt{49-31.36}\\ \\&\Rightarrow&AS&=&\sqrt{17.64}\\ \\&\Rightarrow&AS&=&4.2\end{array}$
D'où, $\boxed{AS=4.2\;cm}$
$-\ $ Calcul de $\tan\hat{A}$
On a :
$$\tan\hat{A}=\dfrac{\text{côté opposé à l'angle }\hat{A}}{\text{côté adjacent à l'angle }\hat{A}}$$
Soit alors : $\tan\hat{A}=\dfrac{RS}{AS}=\dfrac{5.6}{4.2}=1.33$
Ainsi, $\boxed{\tan\hat{A}=1.33}$
5) Soit $E$ le point appartenant à $[RS]\ $ et $\ F$ le point appartenant à $[AS]$, tels que $SE=4.8\;cm\ $ et $\ SF=3.6\;cm.$
Démontrons que $(EF)$ est parallèle à $(RA).$
On a $S\;,\ E\;,\ R$ sont trois points alignés d'une part, et $S\;,\ F\;,\ A$ trois points alignés d'autre part, dans le même ordre.
Calculons les rapports $\dfrac{SE}{RS}\ $ et $\ \dfrac{SF}{AS}$
On a : $\dfrac{SE}{RS}=\dfrac{4.8}{5.6}=0.85\quad$ et $\quad\dfrac{SF}{AS}=\dfrac{3.6}{4.2}=0.85$
Par suite, $\dfrac{SE}{RS}=\dfrac{SF}{AS}$
D'où, les droites $(EF)\ $ et $\ (RA)$ sont parallèles, d'après la réciproque du théorème de Thalès.
Auteur:
Diny Faye

Commentaires
Sokhna maï (non vérifié)
mar, 04/23/2024 - 09:00
Permalien
Réussir
Ajouter un commentaire