Dans une petite et moyenne entreprise ou $PMI$ on étudie la répartition des salaires des travailleurs. 

 

Le schéma ci-dessous en représente l'histogramme des $ECC$ et celui des $ECD$ tracés dans un même repère.

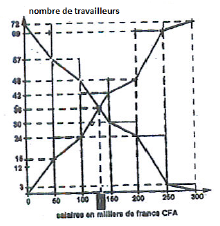
1) Déduis du schéma :

 

a) le caractère étudié puis précise sa nature,$\quad(0.5\;pt)$

 

b) le nombre de travailleurs, dans cette $PMI\;,\quad(0.5\;pt)$

 

c) le nombre de travailleurs qui gagnent au moins 100000 F.$\quad(0.5\;pt)$

 

d) le nombre de travailleurs qui gagnent moins de 150000 F CFA,$\quad(0.5\;pt)$

 

e) le nombre de travailleurs qui gagnent entre 150000 F et 200000 F.$\quad(0.5\;pt)$

 

2) Reproduis avec soin l'histogramme des effectifs cumulés croissants en prenant en abscisses $1\;cm$ pour 50000 F et en ordonnées $0.5\;cm$ pour 3 travailleurs.$\quad(1\;pt)$

 

3) Donne la signification statistique du salaire $R$ sur le schéma.$\quad(1\;pt)$

 

4) Utilise l'histogramme construit précédemment pour calculer la valeur de $R$ à 1 millier de francs près par défaut.$\quad(1.5\;pt)$

On donne les réels $a=5-2\sqrt{5}\;,\ b=1+\dfrac{2}{5}\sqrt{5}\text{ et }c=\dfrac{-5}{5+2\sqrt{5}}$

 

1) Justifie que $a\text{ et }b$ sont des inverses l'un de l'autre.$\quad(1\;pt)$

 

2) Justifie que $a\text{ et }c$ sont opposés.$\quad(1\;pt)$

 

3) Justifie que $c=-\dfrac{1}{b}.\quad(1\;pt)$

 

4) Justifie que $b\times c+1=0.\quad(1\;pt)$

 

5) Encadre $c\text{ à }10^{-2}$ près sachant que $2.237<\sqrt{5}<2.237\quad(1\;pt)$

Soit $EFG$ un triangle rectangle en $E.$

 

Les bissectrices des angles $EFG\text{ et }EGF$ se coupent en $A.$

 

1) Fais une figure.$\quad(1.5\;pt)$

 

2) Calcule la mesure de l'angle $FAG.\quad(1.5\;pt)$

Une bougie décorative à la forme d'un cone de révolution de sommet $S$, de hauteur $27\;cm.$

 

Sa base est un disque de centre $O$ et de rayon $15\;cm$

 

 

Cette bougie est formée de trois parties de couleurs différentes séparées par des plans parallèles au plan de sa base et qui coupent sa hauteur respectivement en $M\text{ et }N$ tels que $SM=MN=ON.$

 

La partie supérieure est en cire de couleur jaune, la partie intermédiaire est de couleur verte et la partie inférieure est bleue.

 

1) a) Montre que la longueur $SM=9\;cm$ puis justifie que le cone de hauteur $SM$ est une réduction de la bougie de coefficient $\dfrac{1}{3}\quad(1\;pt)$

 

b) Le cone de hauteur $SN$ est aussi une réduction de la bougie; calcule le coefficient de réduction.$\quad(0.5\;pt)$

 

2) a) Montre que le rayon de la base du cone de hauteur $SM$ est $5\;cm.\quad(0.5\;pt)$

 

b) Calcule son volume $V_{1}.\quad(1\;pt)$

 

3) a) Calcule le volume $V_{2}$ de la partie intermédiaire.$\quad(1\;pt)$

 

b) Calcule le volume $V_{3}$ de la partie inférieure.$\quad(1\;pt)$

 

c) Exprime $V_{2}\text{ et }V_{3}$ en fonction de $V_{1}.\quad(1\;pt)$