BFEM Mathématiques 1er groupe 2024
Pour chacune des question dans le tableau ci-dessous, trois réponses $A$, $B$ et $C$ sont proposées dont une seule est correcte.
Pour répondre, tu porteras sur ta copie, le numéro de la question suivi
de la lettre correspondant à la réponse choisie.
Chaque réponse correcte est noté $0.75$ points.
Une réponses fausse ou une absence de réponse est notée $0$ points.
$\begin{array}{|c|c|c|c|} \hline N^{°}&\text{Question }&\text{Réponses }A&\text{Réponses }B&\text{Réponses }C\\ \hline 1&\text{Quelle est la valeur du réel }M=\sqrt{\dfrac{2-\sqrt{3}}{2+\sqrt{3}}}?&-2-\sqrt{3}&2-\sqrt{3}&-2+\sqrt{3}\\ \hline 2&\text{Quel est l'ensemble des solution dans }\mathbb{R}\text{de }&{\dfrac{5}{3}\;,2}&]-\infty\;,\dfrac{5}{3}[\cup]2+\infty[&\left[\dfrac{5}{3}\;,2\right]\\ &\text{l'inéquation }(-4x+8)(3x-5)\geq 0?&& \\ \hline &\text{Pour quelles valeurs de }m\text{, le couple }\left(-2\;,m^{2}\right)&m=-2&m=-\sqrt{2}&m=-1\\ 3&\text{est solution de l'équation }-x-y+2=0?&\text{ ou }&\text{ ou }&\text{ ou }\\ &&m=2&m=\sqrt{2}&m=1\\ \hline &\text{Soient }MOI\text{ et }MAB\text{ deux triangle tels que les }&&&\\ &\text{points }M\;,O\;,A\text{d'une part et }M\;,I\;,B\text{d'autre part }&\text{Ellles sont }&\text{Elles sont }&\text{Elles sont}\\ 4&\text{sont alignés dans cet ordre }&\text{sécantes }&\text{perpendiculaires }&\text{parallèles}\\ &\text{Si }\dfrac{MA}{MO}=\dfrac{MB}{MI}\;,\text{quelle est la position relative des}&&&\\ &\text{droites }(OI)\text{et }(AB)?&&&\\ \hline &\text{Soit }MNP\text{un triangle rectangle en }M\text{tel que}&&&\\ 5&\sin\left(\overbrace{MPN}\right)=\dfrac{1}{2}&45^{\circ}&30^{\circ}&60^{\circ}\\ &\text{Quelle est la mesure de l'angle }\overbrace{MNP}?&&&\\ \hline &\text{Soit }\alpha\text{ un réel }&&&\\ 6&\text{Dans le plan muni d'un repère orthonormé, }&8&1&4\\ &\text{pour quelle valeur de }\alpha\;,\text{les vecteurs }\overrightarrow{AB}(\alpha\;,4)&&&\\ &\text{et }\overrightarrow{CD}(-8\;,-2)\text{sont-ils orthogonaux ?}&&&\\ \hline 7&\text{Quelle est l'expression de l'application affine}&\dfrac{1}{3}x^{2}+3&-\dfrac{1}{3}x-5&-\dfrac{1}{3}x+5\\ &h\text{telle que }h(-3)=6?&&&\\ \hline &\text{ Quel est le couple de solution du système }&&&\\ 8&\text{d'équation }\left\lbrace\begin{array}{rcl} 2x-y-1=0\\ 3x+5y&=&21 \end{array}\right. ?&(2\;,3)&(1\;,1)&(7\;,0)\\ \hline \end{array}$
Exercice 2
Les données consignées dans le tableau ci-dessous sont celles de superficies en hectares $(ha)$ attribuées à des habitants d'une région par un Conseil Municipal.
$\begin{array}{|c|c|c|c|c|c|} \hline \text{Superficies }(ha)&]0\;,10]&]10\;,20]&]20\;,30]&]30;,40]&]40\;,50]\\ \hline \text{Effectifs cumulés }&100&60&28&10&4\\ \text{décroissants }&&&&&\\ \hline \end{array}$
Pour que l'attribution des terres soit valables, elle doit être approuvée par le sous-préfet, le préfet, ou le Gouverneur selon la superficie $S$ attribuée.
$\blacktriangleright$ Le sous-préfet approuve une superficies $S$ telle que $S\leq 10\,ha.$
$\blacktriangleright$ Le préfet approuve une superficie $S$ telle que $10\,ha<S\leq50\,ha.$
$\blacktriangleright$ Le gouverneur approuve une superficie $S>50\,ha$
Le Conseil Municipal a besoin de la superficie moyenne $S_{m}$ et de la superficie médiane $S_{me}.$
1. Détermine l'intervalle contenant les superficies attribuées au plus grand nombre d'habitants de la région.
2. En s'appuyant sur les connaissances en statistique, aide ce Conseil Municipal à calculer $S_{m}$ et $S_{me}.$
3.a. Calcule le pourcentage de personnes dont l'attribution des superficies $S$ est approuvée par le sous sous-préfet.
b. Calcule le pourcentage de personnes dont l'attribution des superficies $S$ est approuvée par le Préfet.
Exercice 3
On considère le cercle de centre $O$ et de rayon $R=1.2\,cm$
Les segments $[FA]$ et $[CE]$ sont des diamètres de ce cercle et $\overbrace{OAC}=54^{\circ}$
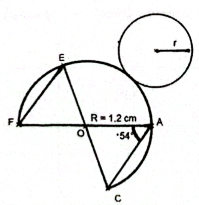
1. Calcule $\overbrace{FOC}$ et $\overbrace{FEC}$
2. Un patron d'un solide est constitué de sa base, un cercle de rayon $r$ et d'un secteur circulaire dont la longueur de l'arc de cercle est égale au périmètre de sa base.
a. Comment appelle-t-on ce solide ?
b. Calcule l'aire latérale $A_{L}$ de la surface de ce solide dont le patron est représenté par la figure ci-dessus.
3. Un groupement d'intérêt Économique $(GIE)$ qui s'active dans la production et la vente de jus locaux veut conserver sa production dans boites représentées par le solide décrit dans la question précédente à l'échelle de $\dfrac{1}{10}$
Sachant que la production journalière en jus remplit un tonneau de forme cylindrique de rayon de base $0.5$ mètre et de hauteur $1.5$ mètre, détermine le nombre maximal de boite que le $GIE$ peut remplir journalière-ment.

Commentaires
Moi (non vérifié)
mer, 07/09/2025 - 17:51
Permalien
https://www.youtube.com/
Ajouter un commentaire