Travail de la force électrostatique - énergie potentielle électrostatique - 1er s
Classe:
Première
I. Travail de la force électrostatique
1. Cas d'un champ uniforme
Considérons une charge négative $q$ se déplaçant dans le champ uniforme $\overrightarrow{E}$ d'un condensateur chargé.
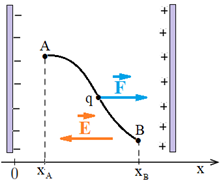
La charge est soumise à la force électrostatique : $\overrightarrow{F}=q\overrightarrow{E}$
Le travail effectué par cette force constante lors du déplacement de la charge du point $A$ au point $B$ est : $W_{AB}\left(\overrightarrow{F}\right)=q\overrightarrow{E}\cdot\overrightarrow{AB}$
Comme le champ électrique est parallèle à l'axe $x$ du repère choisi, le produit scalaire se réduit au produit des coordonnées $x$ des deux vecteurs :
$W_{AB}\left(\overrightarrow{F}\right)=-qE\left(x_{B}-x_{A}\right)$
$\Rightarrow\;W_{AB}\left(\overrightarrow{F}\right)=qE\left(x_{A}-x_{B}\right)$
Le travail de la force électrique est moteur lorsque la charge négative se déplace vers la plaque positive.
La force électrique est conservative, son travail est indépendant de la trajectoire entre $A$ et $B.$
2. Cas d'un champ quelconque
La conclusion obtenue pour le champ uniforme se généralise pour tout champ électrique $\overrightarrow{E}.$
Le travail de la force électrique lors d'un déplacement de $A$ vers $B$ dans un champ quelconque :
$-\ $est proportionnel à la charge électrique transportée $q$
$-\ $dépend du point de départ $A$ et du point d'arrivée $B$ sans dépendre du chemin suivi.$$W_{AB}\left(\overrightarrow{F}\right)=qE\left(x_{A}-x_{B}\right)$$
II. Énergie potentielle électrostatique
1. Relation entre le travail et la variation de l'énergie potentielle
1.1. Expression de l'énergie potentielle électrostatique
Considérons le système composé du condensateur chargé et de la charge négative $q.$
La seule force intérieure est la force électrostatique $\overrightarrow{F}.$
L'énergie potentielle électrostatique $E_{p}$ du système est définie par sa variation lors d'un déplacement de la charge de $A$ vers $B$ :
$\begin{array}{rcl} \Delta E_{p}&=&-W_{AB}\left(\overrightarrow{F}\right)\\\Rightarrow\;E_{p}_{B}-E_{p}_{A}\\&=&-qE\left(x_{A}-x_{B}\right)\\\Rightarrow\;E_{p}_{B}-E_{p}_{A}&=&qE\left(x_{B}-x_{A}\right) \end{array}$
Cette expression détermine l'énergie potentielle électrique en un point d'abscisse $x$ à une constante près : $E_{p}=qEx+\text{cte}$
En choisissant la plaque négative d'abscisse $x=0$ comme niveau de référence pour lequel l'énergie potentielle est nulle.
En un point d'abscisse $x$, l'énergie potentielle électrique s'écrit : $E_{p}=qEx$
Cette énergie est due à la position de la charge dans le champ électrique.
L'énergie potentielle électrique d'une charge négative augmente quand celle-ci s'éloigne de la plaque négative du condensateur.
Remarque :
l'expression reste valable pour une charge positive.
1.2. Potentiel électrique
L'énergie potentielle électrique d'une charge ponctuelle dans un champ électrostatique est proportionnelle à sa valeur $q.$
La grandeur $E_{p}/q$ est indépendante de $q$ et ne dépend que du champ électrostatique et de la position dans le champ.
Cette grandeur électrique est appelée potentiel électrique.
Le potentiel électrique $V$ en un point d'abscisse $x$ d'un champ uniforme $\overrightarrow{E}$ est : $V=E\,x+\text{cte}$
Le potentiel électrique caractérise l'état électrique d'un point où le champ électrique existe
L'unité du potentiel électrique est le volt $(V).$
L'expression de l'énergie potentielle électrique peut s'écrire :
$\begin{array}{rcl} E_{p}&=&qEx+\text{cte}\\\text{Or }V&=&Ex\\\Rightarrow\;E_{p}&=&qV+\text{cte} \end{array}$
Le travail de la force électrostatique effectué sur une charge $q$ entre $A$ et $B$ est :$$W_{AB}\left(\overrightarrow{F}\right)=q\left(V_{A}-V_{B}\right)$$
Remarque :
$-\ $Le potentiel augmente lorsqu'on s'éloigne de la plaque négative et est maximal sur la plaque positive.
$-\ $Comme l'énergie potentielle, le potentiel est définie à une constante près : $V=Ex+\text{cte}$
$-\ $Le potentiel électrique représente l'énergie potentielle électrique d'une charge positive de valeur $1C.$
On déduit de la définition du potentiel l'unité du champ électrique la plus couramment utilisée : $1V/m.$
$-\ $L'électronvolt est unité de mesure de l'énergie électrique : $1eV=1.6\cdot 10^{-19}J$
1.3. Surface équipotentielle
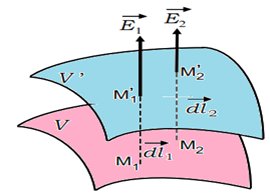
On appelle surface équipotentielle, une surface $S$ dont tous les points sont au même potentiel $V.$
Les lignes de champ sont perpendiculaires aux surfaces équipotentielles qu'elles rencontrent.
Le potentiel décroit le long d'une ligne de champ.
Le champ électrique est plus intense là où les équipotentielles sont les plus resserrées.
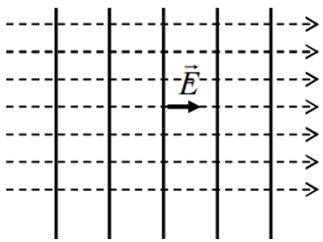
Dans le cas d'un champ uniforme les lignes de champ sont des droites parallèles et les surfaces équipotentielles sont des plans perpendiculaires à ces droites.
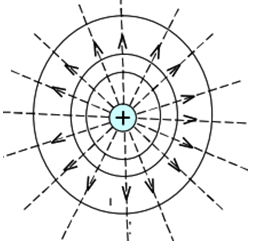
Dans le cas d'une charge ponctuelle, les surfaces équipotentielles sont des sphères concentriques de centre $O$ et les lignes de champ sont radiales
1.4. Différence de potentiel et tension
La valeur du potentiel en un point dépend du choix du niveau de référence.
La différence des potentiels en deux points différents d'un champ électrostatique est indépendante de ce choix et peut être mesurée à l'aide d'un voltmètre.
Cette différence de potentiel est appelée tension électrique.
1.4.1. Définition de la tension électrique
La tension électrique $U_{AB}$ entre deux points $A$ et $B$ d'un champ électrostatique est la différence de potentiel entre ces points :$$U_{AB}=V_{A}-V_{B}$$
Elle est représentée par une flèche orientée de $B$ vers $A$

Ajouter un commentaire