Solution des exercices : Propagation des signaux, ondes progressives, interférences mécaniques - 1er s
Classe:
Première
Exercice 1 Ondes le long d'une corde 1
1) Calcul de la longueur d'onde de l'onde qui se propage sur la corde.
$\begin{array}{rcl} \lambda&=&\dfrac{V}{f}\\&=&\dfrac{8.0}{100}\\\Rightarrow\lambda&=&8.0\cdot 10^{-2}m \end{array}$
2) Comparons le mouvement de la source vibratoire le mouvement d'un point $A$ et celui d'un point $B$
$\begin{array}{rcl} SA&=&k\lambda\\\Rightarrow\;k&=&\dfrac{SA}{\lambda}\\&=&\dfrac{32\cdot10^{-2}}{8.0\cdot10^{-2}}\\\Rightarrow\;k&=&4 \end{array}$
$k$ étant un entier, les points $A$ et $B$ ont le même état vibratoire que la source $S$
Exercice 2 : Ondes le long d'une corde 2
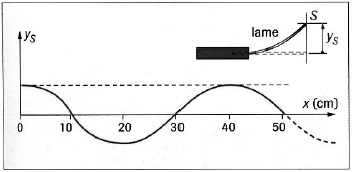
1) Valeur de la période, la longueur d'onde et la célérité de l'onde périodique sinusoïdale
$\begin{array}{rlc} T&=&\dfrac{l}{f}\\&=&\dfrac{l}{100}\\\Rightarrow\;T&=&10^{-2}s \end{array}\ ;$
$\lambda=40\cdot 10^{-2}m$ ;
$\begin{array}{rcl} v&=&\dfrac{\lambda}{T}\\&=&\dfrac{40\cdot 10^{-2}}{10^{-2}}\\\Rightarrow\;v&=&40m\cdot s^{-1} \end{array}$
2) Représentons l'aspect de la corde aux dates
$t+0.0025s=t+\dfrac{T}{4}$ ;
$t+0.0050s=t+\dfrac{T}{2}+0$ ;
$t+0.0075s=t+\dfrac{3T}{4}$ ;
et $t+0.010s=t+T$
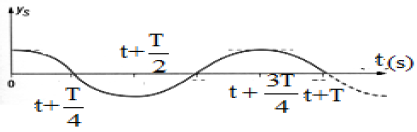
Exercice 3 : Ondes rectilignes sur la cuve à ondes 1
L'onde est longitudinale car la déformation est perpendiculaire à la direction de propagation.
Calcul de la longueur d'onde des ondes
$\begin{array}{rcl} \lambda&=&\dfrac{1}{4}\\&=&\dfrac{16}{4}\\\Rightarrow\lambda&=&4cm \end{array}$
Calcul de la célérité des ondes.
$\begin{array}{rcl} T&=&\dfrac{1}{f}\\&=&\dfrac{1}{50}\\\Rightarrow\;T&=&2\cdot 10^{-2}s \end{array}$
Comparons les mouvements des points $A$ et $B$
Les points $A$ et $B$ sont le même état vibratoire car ils appartiennent à des lignes de même de nature (lignes noires)
Exercice 4 : Ondes circulaires sur la cuve à ondes 2
$-\ $L'onde obtenue est une onde circulaire
$-\ $L'onde est transversale car la perturbation est perpendiculaire à la direction de propagation
$-\ $Calcul de la longueur d'onde des ondes
$\begin{array}{rcl} \lambda&=&\dfrac{d}{4}\\&=&\dfrac{18}{4}\\\Rightarrow\lambda&=&4.5cm \end{array}$
$-\ $Calcul de la célérité des ondes
$\begin{array}{rcl} v&=&f\lambda\\&=&50\times 4.5\cdot 10^{-2}\\\Rightarrow\;v&=&2.25m\cdot s^{-1} \end{array}$
$-\ $Mouvements des points $M$ et $N$ et des mouvements des deux bouchons.
$\begin{array}{rcl} \delta&=&SN-SM\\&=&10.5\cdot 10^{-2}-1.5\cdot 10^{-2}\\\Rightarrow\delta&=&9\cdot 10^{-2}m \end{array}$
$\begin{array}{rcl} \delta&=&k\lambda\\\Rightarrow\;k&=&\dfrac{\delta}{\lambda}\\&=&\dfrac{9\cdot 10^{-2}}{4.5\cdot 10^{-2}}\\\Rightarrow\;k&=&2 \end{array}$
$k$ étant un entier, les points $M$ et $N$, et les deux bouchons ont le même état vibratoire, c'est-à-dire, ils effectuent le même mouvement.
Exercice 5
1. Détermination de l'équation du mouvement d'un point $P$ de la corde d'abscisse $x=SP.$
L'origine $S$ est le siège d'un signal $y_{s}(t)$, à l'instant de date $t$, un point $P$ d'abscisse $x$ reproduira le signal avec un retard $\tau=x/V$: en $P$ le signal est de la forme $y_{s}(t-\tau)$
$\begin{array}{rcl} y_{p}(t)&=&2.\cdot10^{-3}\sin\left(2\pi\cdot N(t-t)\right)\;,\\\text{ or }t&=&\dfrac{x}{V}\\\Rightarrow\;y_{p}(t)&=&2\cdot10^{-3}\sin 2\pi N\left(t-\dfrac{x}{V}\right)\\\Rightarrow\;y_{p}(t)&=&2\cdot10^{-3}\sin\left(2 N\pi t-\dfrac{2 N\pi X}{V}\right)\\\Rightarrow\;y_{p}(t)&=&2\cdot10^{-3}\sin\left(200\pi t-\dfrac{2\pi x}{\gamma}\right) \end{array}$
2. Expression de l'abscisse $x$ de $P$ lorsqu'il vibre :
$\bullet $En phase avec $S$ ; $X=k\lambda$
$\bullet $En opposition de phrase avec $S.$ $x=\left(k+\dfrac{1}{2}\right)\lambda$
3.a. Montrons que $d=5\lambda/2$
$\begin{array}{rcl} d&=&x_{n+2}-x_{n}\\&=&\left(n+2+\dfrac{1}{2}\right)\lambda-n\lambda\\&=&n\lambda+2\lambda+\dfrac{1}{2}\lambda-n\lambda\\\Rightarrow\;d&=&2\lambda+\dfrac{1}{2}\lambda\\\Rightarrow\;d&=&\dfrac{5}{2}\lambda \end{array}$
b. Déduction des valeurs de $\lambda$ et $V$ ;
$\begin{array}{rcl} d&=&\dfrac{5}{2}\lambda\\\Rightarrow\lambda&=&\dfrac{2}{5}d\\&=&\dfrac{2}{5}\times50\\\Rightarrow\lambda&=&20\,cm \end{array}$
$\begin{array}{rcl} V&=&N\lambda\\&=&100\times20\cdot10^{-2}\\ \Rightarrow\;V&=&20\,m\cdot s^{-1} \end{array}$
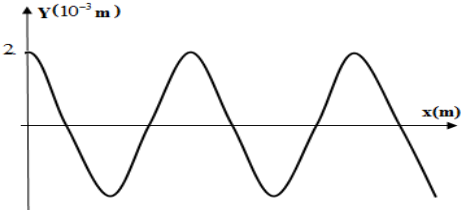
4- Représentation de l'aspect de la corde à l'instant $t_{1}=2.25\cdot10^{-2}s$
$\begin{array}{rcl} y_{p}\left(t_{1}\;,\ x\right)&=&2\cdot10^{-3}\sin\left(200\pi t_{1}-\dfrac{2\pi x}{\lambda}\right)\\&=&2\cdot 10^{-3} \sin\left(200\pi\times 2.25\cdot10^{-2}-\dfrac{2\pi x} {20\cdot10^{-2}}\right)\\\Rightarrow\;y_{p}\left(t_{1}\;,x\right)&=&2\cdot10^{-3}\sin(4.5\pi-10\pi x)\end{array}$
$\begin{array}{rcl} \Rightarrow\;y_{p}\left(t_{1}\;,x\right)&=&2\cdot10^{-3}\sin\left(\dfrac{9\pi}{2}-10\pi x\right)\\\Rightarrow\;y_{p}\left(t_{1}\;,x\right)&=&2\cdot10^{-3}\sin\left(\dfrac{8\pi+\pi}{2}-10\pi x\right)\\&=&2\cdot10^{-3}\sin\left(4\pi+\dfrac{\pi}{2}-10\pi x\right) \end{array}$
$\begin{array}{rcl} &\Rightarrow&\;y_{p}\left(t_{1}\;,x\right)=2\cdot10^{-3}\sin\left(\dfrac{\pi}{2}-10\pi x\right)\\&\Rightarrow&\;y_{p}\left(t_{1}\;,x\right)=2\cdot10^{-3}\cos(10\pi x)\\\text{ avec }x\geq\,vt_{1}&=&20\times \cdot10^{-2}\\&\Rightarrow&\;x\geq45\cdot10^{-2}m\\&\Rightarrow&\;x\geq2.2\gamma \end{array}$
Exercice 6
1. Définition d'une onde.
On appelle onde, le phénomène de propagation d'une perturbation dans un milieu matériel élastique sans
transport de matière ; mais avec transport d'énergie
2. On observe à la surface de l’eau, en lumière ordinaire,
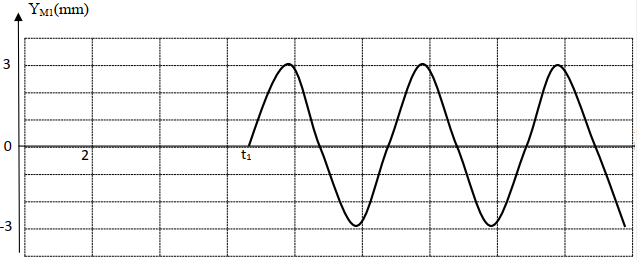
3.1. Détermination de :
$\blacktriangleright$ La fréquence $N$
$\begin{array}{rcl} N&=&\dfrac{1}{T}\\&=&\dfrac{1}{4\cdot 10^{-2}}\\\Rightarrow\;N&=&25Hz \end{array}$
$\blacktriangleright$L'instant $t=7\cdot10^{-2}s$
$\blacktriangleright$La distance $x_{1}$ sachant que la célérité de propagation
$\begin{array}{rcl} x_{1}&=Vt_{1}\\&=&0.25m\cdot s^{-1}\times7\cdot10^{-2}\\\Rightarrow\;x_{1}&=&1.75\cdot10_{-2}m \end{array}$
3.2. Calculer la longueur d'onde $\lambda$
$\begin{array}{rcl} \lambda&=&VT\\&=&0.25\times4\cdot10^{-2}\\\Rightarrow\lambda&=&10^{-2}m \end{array}$
3.3. Détermination de l'équation horaire du mouvement du point $M_{1}$
$\begin{array}{rcl} y&=&3\cdot10^{-3}\sin(2\pi N\left(t-t_{1}\right))\\&=&3\cdot10^{-3}\sin\left(2\pi\times25\left(t-7\cdot10^{-2}\right)\right)\\&=&3\cdot10^{-3}\sin\left(50\pi t-3.5\pi\right)\\&=&3\cdot10^{-3}\sin\left(50\pi t-\dfrac{7}{2}\pi\right) \end{array}$
$\begin{array}{rcl} y_{M_{1}}&=&3\cdot10^{-3}\sin\left(2\pi t-3\pi-\dfrac{1}{2}pi\right)\\&=&3\cdot10^{-3}\sin\left(50\pi t-\pi\dfrac{\pi}{2}\right)\\\Rightarrow\;y_{M_{1}}&=&3\cdot10^{-3}\sin\left(50\pi t-\dfrac{3\pi}{2}\right) \end{array}$
3.4. Déduction de l'équation horaire du mouvement de la source $S.$
$\begin{array}{rcl} Y_{s}&=&Y_{M_{1}}l\left(t+t_{1}\right)\\&=&3\cdot10^{-3}\sin\left(2\pi N\left(t-t_{1}+t_{1}\right)\right)\\&=&3\cdot10^{-3}\sin\left(2\pi Nt\right)\\\Rightarrow\;y&=&3\cdot10^{-3}\sin\left(50\pi t\right) \end{array}$
4. Établissement l'équation horaire du mouvement d'un point $M$
$\begin{array}{rcl} Y&=&3\cdot10^{-3}\sin\left(50\pi\left(t-\dfrac{X}{V}\right)\right)\\&=&3\cdot10^{-3}\sin\left(50\pi t\dfrac{50\pi x}{0.25}\right)\\\Rightarrow\;y&=&3\cdot10^{-3}\sin\left(50\pi t-200\pi x\right) \end{array}$
5. Tracé de l'aspect d'une coupe de la surface de l'eau par un plan vertical passant par S a un instant
$t_{2}=9\cdot10^{-2}s$
$\begin{array}{rcl} y&=&3\cdot10^{-3}\sin\left(50\pi t_{2}-200\pi x\right)\\&=&3\cdot10^{-3}\sin\left(50\pi t-\dfrac{50\pi x}{0.25}\right)\\\Rightarrow\;y&=&3\cdot10^{-3}\sin\left(50\pi t-200\pi x\right) \end{array}$
$\begin{array}{rcl} \left\lbrace\begin{array}{lcl}y=0&\text{si}&x_{2}&\prec&0\\y=3\cdot10^{-3}\sin\left(50\pi t_{2}-200\pi x\right)&\text{si}&x_{2}\leq vt_{2}\end{array}\right.\\&\Rightarrow&\lbrace\begin{array}{lcl} y=0&\text{si}&x_{2}\prec 0\\ y=3\cdot10^{-3}\sin\left(50\pi t_{2}-200pi x\right)&\text{si} &x_{2}\leq vt_{2}=0.25\times9\cdot10^{-2} \end{array}\right.\\&\Rightarrow&\left\rbrace\begin{array}{rcl} y=0&\text{si}&x_{2}\prec 0\\
y=3\cdot10^{-3}\sin(4.5\pi-200\pi x)\text{si}x_{2}\leq2.25\lambda \end{array}\right.\\&\Rightarrow&\left\lbrace\begin{array}{lcl} y=0\text{si}x_{2}\prec 0\\y=3\cdot10^{-3}\sin(\dfrac{\pi}{2}-200\pi x)\text{si}x_{2}\leq 2.25\lambda \end{array}\right. \end{array}$
6.1. On observe en immobilité apparente des rides circulaires constituées de crêtes ou creux
6.2. Détermination des fréquences $N_{e}$ pour lesquelles on observe l'immobilité apparente de la surface de l'eau.
$\begin{array}{rcl} N_{e}=\dfrac{N}{K}\text{ or }10Hz&\leq& N_{e}\\&\leq&100Hz\\\Rightarrow\;10Hz&\leq&\dfrac{N}{K}\\&\leq&100Hz\\\Rightarrow\dfrac{N}{100}&\leq& k\\&\leq&\dfrac{N}{10}\\\Rightarrow\dfrac{25}{100}&\leq& k\leq\dfrac{25}{10}\\\Rightarrow\;0.25&\leq& k\\&\leq&2.5 \end{array}$
$\begin{array}{rcl} k&=&1\\\Rightarrow\;N_{e}&=&\dfrac{25}{1}\\\Rightarrow\;N_{e}&=&25Hz\ ;\ \\k&=&2\\\Rightarrow\;N_{e}&=&\dfrac{25}{2}\\\Rightarrow\;N_{e}&=&12.5Hz \end{array}$
Exercice 7
1. On utilise des absorbants d'énergie au niveau des supports fixes pour éviter les réflexions
2. Description l'aspect de la corde :
En lumière ordinaire, on observe des rides circulaires et une dilution de l'énergie.
En lumière stroboscopique pour une fréquence du stroboscope $N_{e}=25Hz$, on observe une immobilité apparente
3. Calcul de la longueur d'onde $\lambda$
$\begin{array}{rcl} \lambda&=&\dfrac{V}{N}\\&=&\dfrac{5}{50}\\\Rightarrow\lambda&=&0.1\,m \end{array}$
4. Équation du mouvement de la source $S$
$\begin{array}{rcl} Y_{s}&=&-2\cdot10^{-3}\sin100\pi t\\\Rightarrow\;Y_{s}&=&2\cdot 10^{-3}\sin(100\pi t+\pi) \end{array}$
5. Établissement de l'équation de mouvement d'un point $M$ de la corde d'abscisse $x=SM$
$\begin{array}{rcl} Y_{M}&=&2\cdot10^{-3}\sin(100\pi(t-\dfrac{x}{V})+\pi)\\&=&2\cdot10^{-3}\sin(100\pi t-\dfrac{100\pi x}{5}+\pi)\\\Rightarrow\;Y_{M}&=&2\cdot10^{-3}\sin(100\pi t-20\pi x+\pi) \end{array}$
6.1. Déduction de l'équation de mouvement d'un point $M_{1}$ de la corde d'abscisse $x_{1}=17.5\,cm$
$\begin{array}{rcl} \left\lbrace\begin{array}{lcl} Y_{M}(t)=0&\text{si}&t\prec\dfrac{x_{1}}{v}\\ Y_{M_{1}}(t)=2\cdot10^{-3}\sin\left(100\pi t-20\pi x_{1}+\pi\right)&\text{si}&t\geq\dfrac{x_{1}}{v} \end{array}\right.\\\\&\Rightarrow&\left\lbrace\begin{array}{rcl} Y_{M_{1}}=0&\text{si}&t\prec 3.5\cdot10^{-2}s\\Y_{M_{1}}(t)=2\cdot10^{-3}\sin\left(\pi t-20\pi x_{1}+\pi\right)&\text{si}&t\geq3.5\cdot10^{-2}s \end{array}\right.\\\\&\Rightarrow&\left\lbrace\begin{array}{lcl} Y_{M_{1}}(t)=0&\text{si}&t\prec3.5\cdot10^{-2}s\\ Y_{M_{1}}(t)=2\cdot10^{-3}\sin\left(100\pi t-20\pi\times17.5\cdot10^{-2}+\pi\right)&\text{si}&t\geq3.5\cdot10^{-2}s \end{array}\right.\\\\&\Rightarrow&\left\lbrace\begin{array}{lcl} Y_{M_{1}}(t)=0&\text{si}&t\prec3.5\cdot10^{-2}s\\ Y_{M_{1}}(1)=2\cdot10^{-3}\sin(100\pi t-\dfrac{\pi}{2})&\text{si}&t\geq3.5\cdot10^{-2}s \end{array}\right. \end{array}$
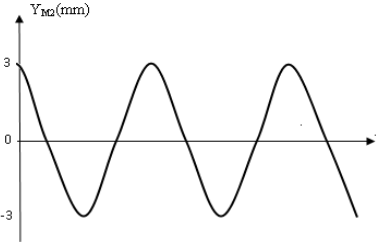
6.2. Représentation sur le même système d'axes $y_{s}(t)$ et $Y_{M_{1}}(t)$
fig109
7. Équation traduisant l'aspect de la corde à la date $t_{2}=0.035s$
$\begin{array}{rcl} Y_{M}\left(_{2}\;,x\right)&=&2\cdot10^{-3}\sin\left(100\pi t_{2}-20\pi x+\pi\right)\\&=&2\cdot10^{-3}\sin(100\pi\times0.035-20\pi x+\pi)\\&=&2\cdot10^{-3}\sin(4.5\pi-20\pi x) Y_{M}(\left(t_{2}\;,x\right)\\&=&2\cdot10^{-3}\sin(\dfrac{9\pi}{2}-20\pi x)\\&=&2\cdot10^{-3}\sin(\dfrac{8\pi+\pi}{2}-20\pi x)\\&=&2\cdot10^{-3}\sin(4\pi+\dfrac{\pi}{2}-20\pi x)\\\Rightarrow\;Y_{M}\left(t_{2}\;,x\right)&=&2\cdot10^{-3}\sin(\dfrac{\pi}{2}-20\pi x)\\\text{avec }vt_{2}\prec x\geq L\\\Rightarrow5\times0.035\prec x\geq0.40\,m\\\Rightarrow0.175\,m\\\Rightarrow11.75\lambda x\geq4.0\lambda \end{array}$
Représentation de l'aspect de la corde à la date $t_{2}$
fig110
8. Détermination du nombre et des positions des points qui vibrent en opposition de phase par rapport à la
source à l'instant $t_{2}$
$\begin{array}{rcl} \varphi_{s}-\varphi_{M}&=&\pi-\left(\dfrac{\pi}{2}-20\pi x\right)\\&=&\pi+2k\pi\\\Rightarrow\pi-\dfrac{\pi}{2}+20\pi x&=&\pi+2k\pi\\\Rightarrow-\dfrac{1}{2}+20x&=&1+2k\\\Rightarrow20x&=&(2k+\dfrac{1}{2})\\\Rightarrow\;x&=&(2k+\dfrac{1}{2}\dfrac{1}{20} \end{array}$
$\begin{array}{rcl} x&=&(2k+\dfrac{1}{2})\dfrac{1}{20}\\\text{or }0\prec x\leq L\\\Rightarrow\;0\prec(2k+\dfrac{1}{2})\dfrac{1}{20}leq0.40\\\Rightarrow0\prec(2k+\dfrac{1}{2})\dfrac{1}{20}\leq 0.40\\\Rightarrow0\times20+\dfrac{1}{2}\prec2k\leq0.40\times20+\dfrac{1}{2}\\\Rightarrow\dfrac{1}{2}\prec 2k\leq8.5\\\Rightarrow0.25\prec k\leq4.25\\\Rightarrow\;k\in{1\;, 2\;, 3\;, 4}x\\&=&(2k+\dfrac{1}{2})\dfrac{1}{20} \end{array}$
$\begin{array}{rcl} k&=&1\\\Rightarrow\;x&=&\left(2\times1+\dfrac{1}{2}\right)\dfrac{1}{20}\\\Rightarrow\;x&=&0.125\,m\ ;\\k&=&2\\\Rightarrow\;x&=&\left(2\times2+\dfrac{1}{2}\right\dfrac{1}{20}\\\Rightarrow\;x&=&0.225\,m\ ;\\k&=&3\\\Rightarrow\;x&=&(2\times 3+\dfrac{1}{2}\dfrac{1}{20}\\\Rightarrow\;x&=&0.325\,m\ ;\\k&=&4\\\Rightarrow;x&=&(2\times4+\dfrac{1}{2}\dfrac{1}{20}\\\Rightarrow\;x&=&0.425\,m \end{array}$
Exercice 8
1.1. Le phénomène résultant de la propagation des déformations à la surface du liquide est appelé onde mécanique transversale car, la perturbation est perpendiculaire à la direction de propagation.
1.2. En lumière ordinaire, on observe des rides circulaires
2. Équation horaire $y_{O}(t)$ du mouvement de $O.$
$\begin{array}{rcl} y_{O}(t)&=&a\sin\left(\omega t+\varphi\right)\\y_{O}(0)&=&a\sin\left(\omega\times 0+\varphi\right)\\&=&0\\\Rightarrow\sin\varphi&=&0\\\Rightarrow\left\lbrace\begin{array}{lcl} \varphi&=&0\\\varphi&=&\pi \end{array}\right.\\\varphi&=&0 \end{array}$
est solution car le point $O$ commence à vibrer en se déplaçant vers le haut
$\begin{array}{rcl} y_{O}(t)&=&a\sin\left(2\pi Nt\right)\\y_{O}(t)&=&5\cdot 10^{-3}\sin\left(2\pi\times 25t\right)\\\Rightarrow\;y_{O}(t)&=&5\cdot 10^{-3}\sin\left(50\pi t\right) \end{array}$
3.1. Définition de la longueur d'onde $\gamma.$
La longueur d'onde est la distance par l'onde cours d'une période temporelle.
3.2. Calcul des valeurs de $\gamma$ et $V.$
$\begin{array}{rcl} V&=&\dfrac{d}{t_{1}}\\&=&\dfrac{8\cdot 10^{-3}}{0.02}\\\Rightarrow\;V&=&0.4m\,m\cdot s^{-1} \end{array}$
$\begin{array}{rcl} \gamma&=&\dfrac{V}{N}\\&=&\dfrac{0.4}{25}\\\Rightarrow\gamma&=&0.016\,m \end{array}$
4.1. Établissement de l'équation horaire $y_{M}(t)$ du mouvement de $M$ en fonction de $r$, $t$ et $\gamma.$
$\begin{array}{rcl} y_{M}(t)&=&2\cdot 10^{-3}\sin\left(2N\pi\left(t-\dfrac{r}{V}\right)\right)\\&=&2\cdot 10^{-3}\sin\left(2N\pi t-\dfrac{2N\pi r}{V}\right)\\&=&2\cdot 10^{-3}\sin\left(2\times 25\pi t-\dfrac{2\pi r}{\gamma}\right)\\\Rightarrow\;y_{M}(t)&=&2\cdot 10^{-3}\sin\left(50\pi t-\dfrac{2\pi r}{\gamma}\right) \end{array}$
4.2. Détermination de l'expression donnant les valeurs de $r$ pour lesquelles le mouvement de $M$ est en opposition de phase avec celui de $O.$
$\begin{array}{rcl} \dfrac{2\pi r}{\gamma}&=&\pi+2k\pi\\\Rightarrow\;2r&=&(1+2k)\gamma\\\Rightarrow\;r&=&(2k+1)\dfrac{\gamma}{2} \end{array}$
5.1. Représentons, en justifiant, une coupe transversale de la surface du liquide suivant un plan vertical passant par $O$, à l'instant de date $t_{2}=7\cdot 10^{-2}s$ de $O$
$\begin{array}{rcl} \left\lbrace\begin{array}{lcl} y_{M}\left(t_{2}\;,\ r\right)=0&\text{si}&r\prec Vt_{2}\\\\y_{M}\left(t_{2}\;,\ r\right)=2\cdot 10^{-3}\sin\left(50\pi t_{2}-\dfrac{2\pi r}{\gamma}\right)&\text{si}&r\leq Vt_{2} \end{array}\right. \\&\Rightarrow&\left\lbrace\begin{array}{lcl} y_{M}\left(t_{2}\;,\ r\right)=0&\text{si}&r\prec 0.4\times 7\cdot 10^{-2}s\\\\y_{M}\left(t_{2}\;,\ r\right)=2\cdot 10^{-3}\sin\left(50\pi\times 7\cdot 10^{-2}s-\dfrac{2\pi r}{\gamma}\right)&\text{si}&r\leq 0.4\times 7\cdot 10^{-2}m \end{array}\right.\\&\Rightarrow&\left\lbrace\begin{array}{lcl} y_{M}\left(t_{2}\;,\ r\right)=0&\text{si}&r\prec 2.8\cdot 10^{-2}s\\\\y_{M}\left(t_{2}\;,\ r\right)=2\cdot 10^{-3}\sin\left(3.5\pi-\dfrac{2\pi r}{\gamma}\right)&\text{si}&r\leq 2.8\cdot 10^{-2}s \end{array}\right.\\&\Rightarrow&\left\lbrace\begin{array}{lcl} y_{M}\left(t_{2}\;,\ r\right)=0&\text{si}&r\prec 2.8\cdot 10^{-2}m\\\\y_{M}\left(t_{2}\;,\ r\right)=2\cdot 10^{-3}\sin\left(\dfrac{2\pi}{2}-\dfrac{2\pi r}{\gamma}\right)&\text{si}&r\leq 2.8\cdot 10^{-2}m \end{array}\right. \end{array}$
5.2. Soit $P$ un point de la surface libre du liquide situé à $r=2\cdot 10^{-2}m$ de $O.$
5.2.1. Détermination de la valeur de la vitesse de ce point à l'instant de date $_{2}$
$\begin{array}{rcl} V_{P}&=&\dfrac{r}{t_{2}}\\&=&\dfrac{2\cdot 10^{-2}}{7\cdot 10^{-2}}\\\Rightarrow\;V_{P}&=&0.3\,m\cdot s^{-1} \end{array}$
5.2.2. Détermination du déphasage du mouvement de $P$ avec celui de $O.$
$\begin{array}{rcl} \varphi&=&\dfrac{2\pi r}{\gamma}\\&=&\dfrac{2\pi\times 10^{-2}}{1.6\cdot 10^{-2}}\\&=&\dfrac{2\pi\times 20}{16}\\&=&\dfrac{2\pi\times 5}{4}\\\Rightarrow\varphi&=&\dfrac{5\pi}{2} \end{array}$
Ce déphasage évolue au cours du temps puisqu'il dépend du point considéré.

Ajouter un commentaire